Weinan E. Principles of Multiscale Modeling

Подождите немного. Документ загружается.

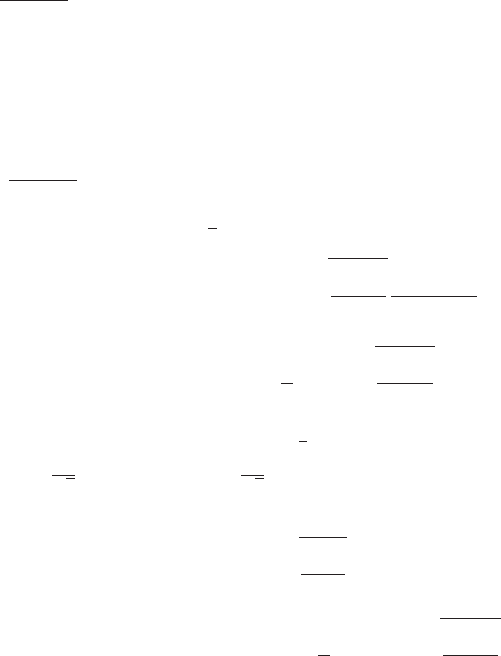
5.1. BROWNIAN DYNAMICS MODELS OF POLYMER FLUIDS 217

We will consider the dumbbell model in the dilute limit of polymer solutions and we

will neglect polymer-polymer interaction. A dumbbell consists of two-beads connected

by a spring. For simplicity, we will assume that the two beads have the same mass and

friction coeﬃcient, denoted by m and ζ respectively. The forces acting on the dumbbells

are:

1. Inertial force m

, i = 1, 2, where the dot denotes time derivative. As mentioned

above, this is neglected in general.

2. Frictional force −ζ



− u(r

)



, i = 1, 2.

3. Spring force F

= −∇

Ψ(r

, r

), i = 1, 2, where Ψ is the potential energy for the

spring. The choice of the potential Ψ will be discussed later. In general, we should

have F

+ F

= 0.

4. Brownian force η

= σ

, i = 1, 2, where

and

are independent white noises,

σ =

√

T ζ by the ﬂuctuation-dissipation theorem.

Force balance gives:

ζ(

− u(r

)) = F

+ σ

, (5.1.6)

ζ(

− u(r

)) = F

+ σ

(5.1.7)

where σ =

√

T ζ. If we add and subtract the two equations, we obtain the equations

for the center of resistance r

+ r

) and the conformation vector Q = r

− r

;

= u(r

) +

(5.1.8)

Q = ∇u(r

)Q −

(

−

). (5.1.9)

Here we have made the approximation:

(u(r

) + u(r

)) ∼ u(r

) and u(r

) − u(r

) ∼

∇u(r

)Q. Since

√

− w

) and

√

+ w

) are independent standard Wiener pro-

cesses, we canb rewrite the two equations above as

= u(r

) +

, (5.1.10)

Q = ∇u(r

)Q −

F(Q) +

. (5.1.11)

218 CHAPTER 5. EXAMPLES OF MULTI-PHYSICS MODELS

where

and

are standard independent white noises.

We now turn to the potential of the spring force. Two most commonly used models

are:

1. Hookean sp ring: The spring force is HQ and the potential is given by

H|Q|

Here H is the spring constant.

2. FENE (Finitely Extensible Nonlinear Elastic) spring: The spring force is

1−(|Q|/Q

)

and the potential is given by −

H|Q|



1 −(|Q|/Q

)



. Here Q

is the maximal

extension of the FENE spring.

The probability d ensity function (pdf) ψ(x, Q, t) of the dumbbells satisﬁes the Fokker-

Planck equation, also known as the Smoluchowski equation [18, 28, 29]

∂

ψ + ∇ · (uψ) + ∇



(∇u)Q −

F)ψ



∆

ψ +

2ζ

∆ψ (5.1.12)

So far we have discussed how to model the dynamics of the dumbbells in the solvent.

Next, we will discuss how the dumbbells inﬂuence the dynamics of the solvent. To this

end, we need an expression for the polymer component of the stress, τ

. Imagine a plane

immersed inside the polymer ﬂuid. There are two kinds of contributions that we need to

consider [3]:

1. The spring force due to the dumbbells that straddle the plane. This part will be

denoted as τ

(c)

2. Momentum transfer caused by the crossing of the dumbbells through the plane.

This part will be denoted as τ

(b)

We ﬁrst discuss τ

(c)

. Denote by n the number density of the polymer. Let us consider

a cube of volume 1/n. Given a dumbbell with orientation Q in this region, the probability

that it will cut the shaded plane is (Q · n)/(1/n)

1/3

, where n is the unit normal vector

of the plane. The force in the spring is F(Q). Averaging over Q, we obtain

Q · n

(1/n)

1/3

F(Q)ψ(x, Q, t)dQ. (5.1.13)

The area of the plane within the cube is n

−2/3

. Therefore the force per area is nh(Q ·

n)F(Q)i = n · τ

(c)

. Hence this part of the contribution to the stress is

(c)

= nhQ ⊗ F(Q)i, (5.1.14)

5.1. BROWNIAN DYNAMICS MODELS OF POLYMER FLUIDS 219

Arbitrary plane

Cube of volume 1/n

Figure 5.2: Illustration of the derivation of the formula

for the stress τ

(c)

– contributions coming from the con-

nectors Q that intersect with the control surface (cour-

tesy of Tiejun Li).

where h·i denotes ensemble averaging in Q space.

Next, we turn to τ

(b)

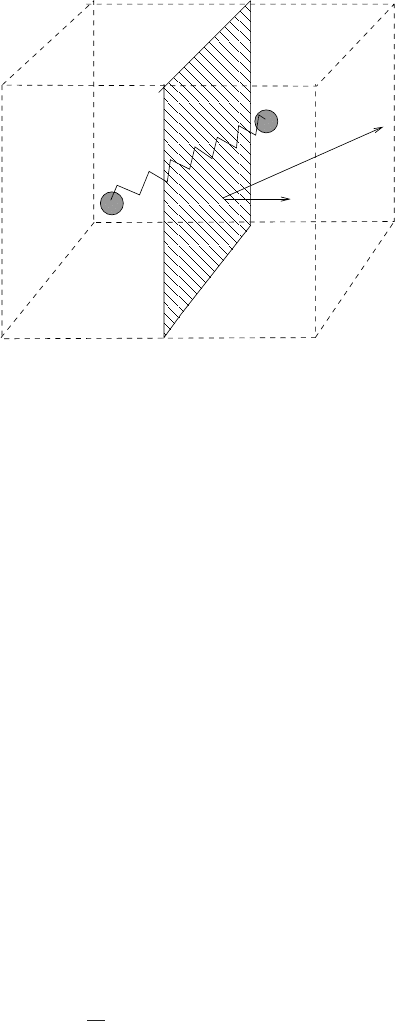
. Consider a moving plane with velocity u. Each dumbbell has

two beads, which we label as 1 and 2 respectively. The number of bead 1 with velocity

that crosses the surface with area S per unit time will be −n(

− u) · nS. The amount

of momentum transported as a result is

−n((

− u) ·nS)m(

− u). (5.1.15)

There is a similar expression for bead 2. The total momentum transported will be

−

Z Z

i=1

n((

− u) · nS)m(

− u)Ψ(

. (5.1.16)

Assuming a Maxwellian distribution for the velocity of the beads Ψ(

Ψ(

) =

exp



−



− u)

+ m(

− u)



/2k



(5.1.17)

where Z =

exp(−(m(

− u)

+ m(

− u)

)/2k

T )d

, we can easily show that

the mean momentum transported is equal to −2nk

T I · nS = Sn · τ

(b)

. Hence

(b)

= −2nk

T I (5.1.18)

220 CHAPTER 5. EXAMPLES OF MULTI-PHYSICS MODELS

Area S

(

moving velocity of the plane:

−

u )dt

Figure 5.3: Illustration of the derivation of the formula

for the stress τ

(b)

– contributions from the transportation

of the momentum by the dumbbells (courtesy of Tiejun

Li).

Out of this, −nk

T I is the contribution to the pressure. The remaining part gives

(b)

= −nk

T I. (5.1.19)

Combining (5.1.14) and (5.1.19), we obtain Kramers’ expression for the polymeric

stress in the dumbbell model:

= −nk

T I + nhF(Q) ⊗ Qi. (5.1.20)

It is a standard practice to drop the term −nk

T I since it can be lumped into the

pressure.

To non-dimensionalize the model, we use:

x → L

x, Q → l

Q, u → U

u, t → t, p → P

p (5.1.21)

where L

and U

are typical length and velocity scales for the ﬂuid ﬂow respectively, and

, T

= L

, P

= ρ

(5.1.22)

5.1. BROWNIAN DYNAMICS MODELS OF POLYMER FLUIDS 221

In addition, deﬁne

De =

, Re =

, ε =

, γ =

, (5.1.23)

where T

= ζ/(4H) is the relaxation time scale of the spring, ρ

is the density and η

is the total viscosity of the ﬂuid. De is called the Deborah number. Re and γ are the

Reynolds number and viscosity ratio, respectively. A standard non-dimensionalization

procedure gives:

∂

u + (u · ∇)u + ∇p =

∆u +

1 − γ

ReDe

∇ · τ

, (5.1.24)

∇ · u = 0, (5.1.25)

= hF(Q) ⊗Qi, (5.1.26)

= u(x) +

√

(t), (5.1.27)

= ∇u · Q −

2De

F(Q) +

√

(t). (5.1.28)

Here the ensemble average in (5.1.26) is deﬁned with respect to the realizations of the

white noises in (5.1.27) and (5.1.28). To simulate this model numerically, one needs to

start with an ensemble of Brownian particles, whose dynamics are governed by (5.1.27)

and (5.1.28). One obtains a set of quantities {(x

, Q

)} for the ensemble. The polymer

stress τ

can be computed by averaging the quantity in (5.1.26). Since ε in general is

very small, it is customary to neglect the Brownian force in (5.1.27). A more precise

derivation of these equations can be found in [2].

(5.1.24) - (5.1.28) is a model for the dynamics of dilute polymer solution. One can see

that the polymers are modeled by non-interacting Brownian particles. Their inﬂuence

to each other is only felt through the ﬂow. In addition, particles initiated at the same

location will always stay at the same location. In this case, instead of tracking the position

and conformation (x, Q) of each particle, on e can model the stochastic dynamics of the

conformation by the dynamics of a conformation ﬁeld Q(x, t): Q(x, t) is the conformation

of a Brownian particle at location x and time t [41]. Combining (5.1.27) and (5.1.28)

gives [41]

∂

Q + (u · ∇)Q = ∇u · Q −

2De

F(Q) +

√

W(t). (5.1.29)

Note that in this model, the noise term is independent of the sp ace variable x. The

222 CHAPTER 5. EXAMPLES OF MULTI-PHYSICS MODELS

corresponding Smoluchowski equation is:

∂

ψ + ∇ · (uψ) + ∇



(∇u · Q −

2De

F(Q))ψ



2De

∆

ψ. (5.1.30)

(5.1.30) can be regarded as the Fokker-Planck equation for the Brownian conﬁguration

ﬁelds. It can also be regarded as the kinetic equation for the Brownian particles in the

(x, Q) space. The dependen ce on velocity or momentum variables is absent, since we

have assumed that it is Maxwellian (see (5.1.17)).

The model we just arrived at is an example of the coupled macro-micro models: The

macroscale Navier-Stokes-like system (5.1.24) - (5.1.25) for the velocity ﬁeld is coupled

with the microscale Brownian dynamics model (5.1.27)-(5.1.28) for the conformation

dynamics of the polymers.

5.2 Extensions of the Cauchy-Born rule

In S ection 4.2, we discussed how one can derive continuum nonlinear elasticity models

from the atomistic models using the Cauchy-Born rule. The discussion was limited to

bulk crystals whose elastic energy takes the form:

E({u}) =

Ω

W (∇u)dx (5.2.1)

In this section, we will discuss the extension to situations when higher order eﬀects, such

as the eﬀects of strain gradients, are important

E({u}) =

Ω

W (∇u, ∇

u, ···)dx. (5.2.2)

This is the case when the crystal is small, or at least one of the dimensions of the crystal

is small, as is the case for rods, sheets, or thin ﬁlms.

The essence of the Cauchy-Born rule is that locally, one can approximate the dis-

placement ﬁeld by a homogeneous deformation, i.e. linear approximation:

u(x) ≈

(x) = u(x

) + (∇u)(x

)(x − x

= x

) (5.2.3)

for each x

, where x

is close to x

(say in the interaction range of x

. This expression is

then used in the atomistic energy to give a continuum energy density that depends only

on ∇u.

5.2. EXTENSIONS OF THE CAUCHY-BORN RULE 223

5.2.1 High order, exponential and local Cauchy-Born rules

(5.2.3) uses only th e leading order approximation in the Taylor expansion. A straight-

forward extension is to use higher order approximation:

u(x) ≈

(x) =u(x

) + (∇u)(x

)(x − x

) (5.2.4)

(∇

u)(x

) : (x − x

) ⊗ (x − x

) (5.2.5)

If we proceed in the same way as before with this new approximation, we obtain a stored

energy density that depends on both ∇u and ∇

u [7, 22]:

W = W

HCB

(∇u(x), ∇

u(x)) (5.2.6)

This is an example of the high order Cauchy-Born rule.

When curvature eﬀects are important, as is the case for rods, thin ﬁlms and sheets,

these Cauchy-Born rules should be modiﬁed accordingly. One approach is to use the ex-

ponential map which maps curved objects, such as surfaces, to their tangent spaces. The

other approach is to make use of the local Taylor expansion. The resulting Cauchy-Born

approximations are called the exponential Cauchy-Born rule [1] and the local Cauchy-

Born rule [46] respectively. As before, their main ingredient is a kinematic approximation

to the positions of the atoms in the neighborhood of a given atom. Instead of describing

the abstract procedure, we will illustrate these ideas using some simple examples.

5.2.2 An example of a one-dimensional chain

Consider a one-dimensional chain of atoms on the plane. Before deformation, the

atoms are on a straight line, with positions {x

}, x

= ja. To be speciﬁc, we will assume

that the energy of the system takes the form:

V =

i,j,k

V (y

, y

) =

(5.2.7)

where

j,k

V (y

, y

) (5.2.8)

We will ﬁrst discuss the exponential Cauchy-Born rule. Assume that the chain is

deformed to a smooth curve on the plane. Assume that the local deformation gradient

224 CHAPTER 5. EXAMPLES OF MULTI-PHYSICS MODELS

(here the stretching or compression ratio) at x

is F and the curvature after deformation

is κ. In order to ﬁnd the approximate position of neighboring atoms after the chain is

deformed, we consider the eﬀects of stretching /compression and curvature separately.

After stretching /compression, the atom at x

is mapped to

˜y

= x

+ (1 + F )(x

− x

) (5.2.9)

On the other hand, curvature alone will map x

+ sin(κ(x

− x

))/κ

(1 − cos(κ(x

− x

)))/κ

The composition of the two maps gives us:

+ sin((1 + F )κ(x

− x

))/κ

(1 − cos((1 + F )κ(x

− x

)))/κ

. (5.2.10)

Substituting into (5.2.7), we obtain the energy density as a function of F and κ:

W (F, κ)(x

) =

j,k

V (

) (5.2.11)

where

= (x

, 0)

and

are given by (5.2.10).

Next we consider the local Cauchy-Born rule. The displacement is now speciﬁed by

the vector ﬁeld u = (u(x), v(x))

. At x

, we approximate the deformed position of the

neighboring atoms by:

= (x

, 0)

+ u(x

) +

)(x

− x

) +

)(x

− x

)

. (5.2.12)

Substituting into (5.2.7), we obtain the energy density as a function of

) and

)



)



j,k

V (

) (5.2.13)

where again

= (x

, 0)

and

are given by (5.2.12).

We can relate these two results using the simple relation:

F = |e

| − 1, (5.2.14)

κ =



) ×



(5.2.15)

where e

= (1, 0)

5.2. EXTENSIONS OF THE CAUCHY-BORN RULE 225

5.2.3 Sheets and nanotubes

Sheets are two-dimensional surfaces. Examples of sheet-like structures include the

grapheen sheet and the carbon nanotube. These structures can sustain very large elastic

deformation. To model such large deformation, we have to have an accurate nonlinear

elasticity model. Naturally, one way of getting such a model is to derive it from an

accurate atomistic model.

For simplicity, we will assume that the reference conﬁguration is a ﬂat sheet that

occupies the x

− x

plane. After deformation, atoms on the sheet are mapped to:













→































, x

)

, x

)

, x

)







. (5.2.16)

For nanotubes, the reference conﬁguration should be a cylinder. However, this does not

change much the discussion that follows.

As before, we start with an accurate atomistic model, which for simplicity will be

expressed as a three-body potential. We will look for a set of kinematic approximations

that will convert the atomistic model to a continuum model.

The exponential Cauchy-Born rule

As before, to apply the exponential Cauchy-Born rule [1], we proceed in two steps:

1. Step 1: Deforming the tangent plane.

2. Step 2: Using the exponential map to take into account the curvature eﬀect.

In practice, the exponential map is approximated by a combination of two consecutive

deformations along the two principal curvature directions. The two principal curvatures

, κ

can be calculated by diagonalizing the curvature tensor κ. Without loss of gener-

ality, we can assume that κ takes a simple diagonal form κ = diag{κ

, κ

}. In this way,

the kinematic approximation can be expressed using a three-step procedure:

1. Deform the tangent plane using the 2D deformation gradient tensor F = ∇u as in

the standard Cauchy-Born rule

w =

= (I + F) · x = (I + F) ·

(5.2.17)

226 CHAPTER 5. EXAMPLES OF MULTI-PHYSICS MODELS

2. Roll the plane into a cylinder with curvature κ

along the ﬁrst principal curvature

direction to obtain the ﬁrst curvature correction

∆w







sin(κ

)/κ

− w

(1 − cos(κ

))/κ







3. Roll the plane into a cylinder with curvature κ

along the second principal curvature

direction to obtain the second curvature correction

∆w







sin(κ

)/κ

− w

(1 − cos(κ

))/κ







The deformed position of y is then given by:

y = w + ∆w

+ ∆w







η(κ

)

η(κ

)

(κ

/2)/2 + κ

(κ

/2)/2







(5.2.18)

where η(x) = sin(x)/x, the two dimensional vector w = (w

, w

) is identiﬁed with the

three dimensional vector w = (w

, w

, 0).

The exponential Cauchy-Born rule has been used extensively by Arroyo and Be-

lytschko to study the mechanical deformation of both single- and multi-walled nanotubes

(see [1]). An example of their results is shown in Figure 5.2.3.

The local Cauchy-Born rule

At each point x

= (x

i,1

, x

i,2

) on the sheet, we approximate the displaced position of