Wallace J.M., Hobbs P.V. Atmospheric Science. An Introductory Survey
Подождите немного. Документ загружается.

144 Radiative Transfer
the departures of the temperatures from some pre-
scribed “reference sounding” defined at a prescribed
set of levels using standard linear regression tech-
niques. The reference sounding incorporates in situ
data capable of resolving features such as the
tropopause that tend to be smoothed out in the
retrievals based on solutions of the radiative transfer
equations. Statistically based temperature and mois-
ture retrievals are carried out routinely as an integral
part of the multivariate data assimilation protocols,
as explained in the supplement to Chapter 8 on the
book Web site.
4.6 Radiation Balance at the Top
of the Atmosphere
This chapter concludes with a brief survey of some of
the global fields relating to the energy balance at the
top of the atmosphere, defined on the basis of the
analysis of 1 year of satellite observations. The map
projection used in this section is area preserving, so
that the maps presented here can be interpreted as
depicting local contributions to global-mean quantities.
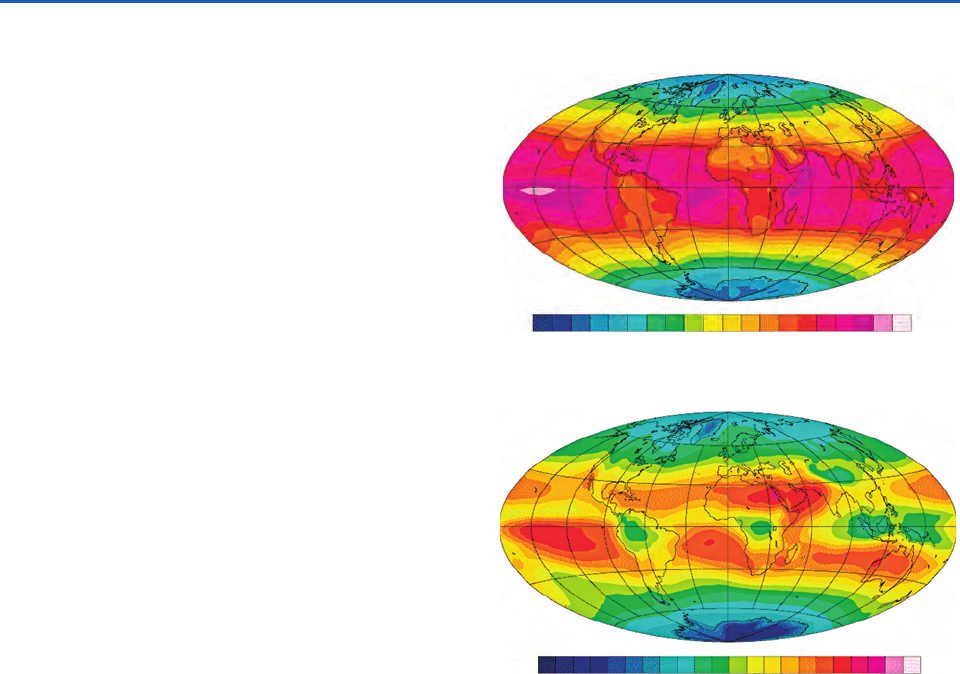
The top image in Fig. 4.34 shows the annual mean net
(downward) shortwave radiation, taking into account
the geographical variations in solar declination angle
and local albedo. Values are 300Wm
2
in the trop-
ics, where the sun is nearly directly overhead at midday
throughout the year. Within the tropics the highest
values are observed over cloud-free regions of the
oceans, where annual-mean local albedos range as low
as 0.1, and the lowest values are observed over the
deserts where albedos are 0.2 and locally range as
high as 0.35. Net incoming solar radiation drops below
100Wm
2
in the polar regions where winters are dark
and the continuous summer daylight is offset by the
high solar zenith angles, widespread cloudiness, and the
high albedo of ice-covered surfaces.
The corresponding distribution of outgoing long-
wave radiation (OLR) at the top of the atmosphere,
shown in the bottom image in Fig. 4.34, exhibits a
gentler equator-to-pole gradient and more regional
variability within the tropics. As shown in Exercise
4.56, the observed equator-to-pole contrast in surface
air temperature is sufficient to produce a 2:1 differ-
ence in outgoing OLR between the equator and the
polar regions, but this is partially offset by the fact
that cloud tops and the top of the moist layer are
higher in the tropics than over high latitudes. The
regions of conspicuously low OLR over Indonesia
and parts of the tropical continents reflect the preva-
lence of deep convective clouds with high, cold tops:
the intertropical convergence zone is also evident as
a local OLR minimum, but it is not as pronounced
because the cloud tops are not as high as those asso-
ciated with convection over the continents and the
extreme western Pacific and Indonesia. Areas with
the highest annual mean OLR are the deserts and
the equatorial dry zones over the tropical Pacific,
where the atmosphere is relatively dry and cloud
free, allowing more of the radiation emitted by the
Earth’s surface to escape unimpeded.
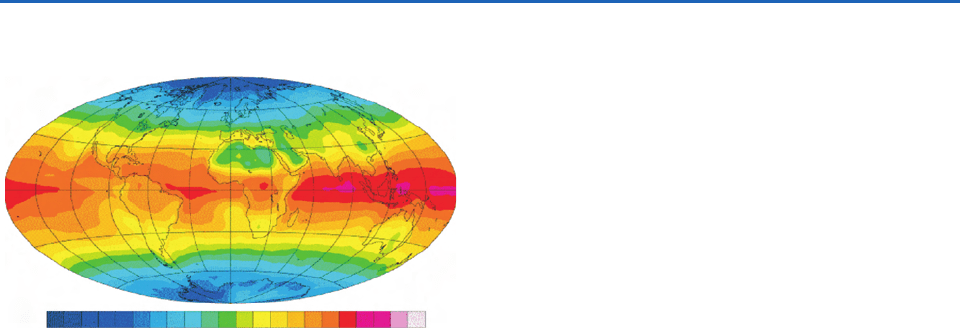
The net downward radiation at the top of the
atmosphere (i.e., the imbalance between net solar
and outgoing longwave radiation at the top of the
atmosphere) obtained by taking the difference
between the two panels of Fig. 4.34 is shown in
Fig. 4.35. The surplus of incoming solar radiation
over outgoing longwave radiation in low latitudes
and the deficit in high latitudes has important impli-
W
m
–2
Absorbed Solar Radiation
0 40 80 120 160 200 240 280 320 360 410
W m
–2
Outgoing Longwave Radiation
110
130 150 170 190 210 230 250 270 290
310 330
Fig. 4.34 Global distributions of the annual-mean radiation
at the top of the atmosphere. [Based on data from the NASA
Earth Radiation Budget Experiment. Courtesy of Dennis L.
Hartmann.]
P732951-Ch04.qxd 12/16/05 11:04 AM Page 144
Exercises 145
cations for the global energy balance, as discussed in
Section 10.1. It is notable that over some of the
world’s hottest desert regions, the outgoing longwave
radiation exceeds absorbed solar radiation.
The exclusive focus on radiative fluxes in this sec-
tion is justified by the fact that radiative transfer is
the only process capable of exchanging energy
between the Earth and the rest of the universe. The
energy balance at the Earth’s surface is more compli-
cated because conduction of latent and sensible heat
across the Earth’s surface also plays important roles,
as discussed in Chapter 9.
Exercises
4.11 Explain or interpret the following in terms of
the principles discussed in this chapter.
(a) Species of plants that require a relatively
cool, moist environment tend to grow on
poleward-facing slopes.
(b) On a clear day a snow surface is much
brighter when the sun is nearly overhead
than when it is just above the horizon.
(c) Light-colored clothing is often worn in hot
climates.
(d) The stars twinkle, whereas the planets do not.
(e) The radiation emitted by the sun is isotropic,
yet solar radiation incident on the Earth’s
atmosphere may be regarded as parallel
beam.
(f) The colors of the stars are related to their
temperatures, whereas the colors of the
planets are not.
(g) The color temperature of the sun is slightly
different from its equivalent blackbody
temperature.
(h) The equivalent blackbody temperature of
Venus is lower than that of Earth even
though Venus is closer to the sun.
(i) The equivalent blackbody temperature of
the Earth is lower than the global-mean
surface temperature by 34 °C.
(j) Frost may form on the ground when
temperatures just above the ground are
above freezing.
(k) At night if air temperatures are uniform,
frost on highways is likely to form first on
bridges and hilltops.
(l) Aerosols in the atmosphere (or on
windows) are more clearly visible when
viewed looking toward a light source than
away from it.
(m) Clouds behave as blackbodies in the infrared
region of the spectrum, but are relatively
transparent in the microwave region.
(n) Sunlit objects appear reddish around
sunrise and sunset on days when the air is
relatively free of aerosols.
(o) A given mass of liquid water would produce
more scattering if it were distributed among
a large number of small cloud droplets than
among a smaller number of larger droplets
(assume that both sizes of droplets fall
within the geometric optics regime).
(p) The upper layers of the atmosphere in
Fig. 4.36 appear blue, whereas the lower
layers appear red.
(q) Smoke particles with a radius of 0.5 mm
appear bluish when viewed against a dark
background but reddish when viewed
against a light background (e.g., the sky).
(r) The disk of the full moon appears uniformly
bright all the way out to the edge.
(s) The absorption coefficient of a gas is a
function of temperature and pressure.
(t) The absorptivity of greenhouse gases in the
troposphere is enhanced by the presence of
high concentrations of N
2
and O
2
.
–180 –150 –120 –90 –60 –30 0 30 60 90 120 150
Net Radiation
W m
–2
Fig. 4.35 Global distribution of the net imbalance between
the annual-mean net incoming solar radiation and the outgo-
ing longwave radiation. Positive values indicate a downward
flux. [Based on data from the NASA Earth Radiation Budget
Experiment. Courtesy of Dennis L. Hartmann.]
P732951-Ch04.qxd 12/16/05 11:04 AM Page 145

146 Radiative Transfer
(u) Low clouds emit more infrared radiation
than high clouds of comparable optical
thickness.
(v) The presence of cloud cover tends to favor
lower daytime surface temperatures and
higher nighttime surface temperatures.
(w) Temperature inversions tend to form at
night immediately above the tops of cloud
layers.
(x) Convection cells are often observed within
cloud layers.
(y) At night, when a surface based inversion is
present, surface temperatures tend to rise
when a deck of low clouds moves overhead.
(z) Low clouds are not visible in satellite
imagery in the water vapor channel.
(aa) Ground fog is more clearly evident in
visible than in infrared satellite imagery.
(bb) The fraction of the incoming solar
radiation that is backscattered to space by
clouds is higher when the sun is low in the
sky than when it is overhead.
(cc) Under what conditions can the flux density
of solar radiation at the Earth’s surface
(locally) be greater than that at the top of
the atmosphere?
4.12 Remote sensing in the microwave part of the
spectrum relies on radiation emitted by oxygen
molecules at frequencies near 55 GHz.
Calculate the wavelength and wave number of
this radiation.
4.13 The spectrum of monochromatic intensity can
be defined either in terms of wavelength
or
wave number
such that the area under
the spectrum, plotted as a linear function of
or
, is proportional to intensity. Show that
I
2
I
.
4.14 A body is emitting radiation with the following
idealized spectrum of monochromatic flux
density.
Calculate the flux density of the radiation.
4.15 An opaque surface with the following
absorption spectrum is subjected to the
radiation described in the previous exercise:
How much of the radiation is absorbed? How
much is reflected?
4.16 Calculate the ratios of the incident solar
radiation at noon on north- and south-facing
5° slopes (relative to the horizon) in seasons
in which the solar zenith angle is (a) 30° and
(b) 60°.
0.70
m
0.70
m
0
1
F
0
F
1.0 W m
2
m
1
F
0.5 W m
2
m
1
F
0.2 W m
2
m
1
F
0
0.35
m
0.35
m
0.50
m
0.50
m
0.70
m
0.70
m
1.00
m
1.00
m
Fig. 4.36 In these views of the limb of the Earth from space,
the upper atmosphere shows up blue, while the lower atmos-
phere exhibits an orange hue. The lower photo, taken 2
months after the eruption of Mt. Pinatubo, shows layers of
sulfate aerosols in the lower stratosphere. [Photographs cour-
tesy of NASA.]
P732951-Ch04.qxd 12/16/05 11:04 AM Page 146

Exercises 147
4.17 Compute the daily insolation at the North Pole
at the time of the summer solstice when the
Earth–sun distance is 1.52 10
8
km.The tilt of
the Earth’s axis is 23.5°.
4.18 Compute the daily insolation at the top of
the atmosphere at the equator at the time of
the equinox (a) by integrating the flux density
over a 24-h period and (b) by simple geometric
considerations. Compare your result with
the value in the previous exercise and with
Fig. 10.5.
4.19 Orbitally induced variations in solar flux
density incident in the top of the atmosphere
during summer at high latitudes of the
northern hemisphere play a central role in the
orbital theory of the ice ages discussed in
Section 2.5.3. By what factor does the flux
density at noon, at 55 °N on the day of the
summer solstice, vary between the extremes of
the orbital cycles?
4.20 What fraction of the flux of energy emitted by
the sun does the Earth intercept?
4.21 Show that for small perturbations in the Earth’s
radiation balance
where T
E
is the Earth’s equivalent blackbody
temperature and F
E
is the flux density of
radiation emitted from the top of its
atmosphere. [Hint: Take the logarithm of the
Stefan–Boltzmann law (4.12) and then take the
differential.] Use this relationship to estimate
the change in equivalent blackbody
temperature that would occur in response to
(a) the seasonal variations in the sun–Earth
distance due to the eccentricity of the Earth’s
orbit (presently 3.5%) and (b) an increase in
the Earth’s albedo from 0.305 to 0.315.
4.22 Show that the flux density of incident solar
radiation on any planet in the solar system is
1368 W m
2
r
2
, where r is the planet–sun
distance, expressed in astronomical units.
4.23 Estimate the flux density of the radiation
emitted from the solar photosphere using two
different approaches: (a) starting with the
intensity (2.00 10
7
W m
2
sr
1
) and making
use of the results in Exercise 4.3 and
T
E
T
E
1
4
F
E
F
E
(b) making use of the relationship derived in
the previous exercise. (c) Estimate the output
of the sun in watts.
4.24 By differentiating the Planck function (4.10),
derive Wien’s displacement law. [Hint: in the
wavelength range of interest, the exponential
term in the denominator of (4.10) is much
larger than 1.]
4.25 Show that for radiation with very long
wavelengths, the Planck monochromatic
intensity B
(T) is linearly proportional to
absolute temperature.This is referred to as the
Rayleigh–Jeans limit.
4.26 Use the relationship derived in Exercise 4.22 to
check the numerical values of T
E
in Table 4.1.
4.27 The observed equivalent blackbody
temperature of Jupiter is 125 K, 20 K higher
than the value in Table 4.1. Assuming that the
temperature of Jupiter is in a steady state,
estimate the flux density of radiation emitted
from the top of its atmosphere that is generated
internally by processes on the planet.
4.28 If the moon subtends the same arc of solid
angle in the sky that the sun does and it is
directly overhead, prove that the flux density of
moonlight on a horizontal surface on Earth is
given by F
s
a(R
s
d)
2
, where F
s
is the flux
density of solar radiation intercepted by the
Earth, a is the moon’s albedo, R
s
is the radius
of the sun, and d is the Earth–sun distance.
Estimate the flux density of moonlight
under these conditions, assuming a lunar
albedo of 0.07.
4.29 Suppose that the sun’s emission or the Earth’s
albedo were to change abruptly by a small
increment. Show that the radiative relaxation
rate for the atmosphere (i.e., the initial rate at
which the Earth’s equivalent blackbody
temperature would respond to the change,
assuming that the atmosphere is thermally
isolated from the other components of the
Earth system) is given by
where
T
E
is the initial departure of the
equivalent blackbody temperature from
radiative equilibrium,
is the Stefan–
Boltzmann constant, T
E
is the equivalent
dT
dt
4
T
3
E
T
E
c
p
p
s
1
P732951-Ch04.qxd 12/16/05 11:04 AM Page 147

148 Radiative Transfer
blackbody temperature in K, c
p
is the specific
heat of air, p
s
is the global-mean surface
pressure, and g is the gravitational acceleration.
The time
T
E
(dT/dt)
1
required for the
atmosphere to fully adjust to the change in
radiative forcing, if this initial time rate of
change of temperature were maintained until
the new equilibrium was established, is called
the radiative relaxation time. Estimate the
radiative relaxation time for the Earth’s
atmosphere.
4.30 A small, perfectly black, spherical satellite is in
orbit around the Earth at an altitude of 2000
km as depicted in Fig. 4.37. What angle does the
Earth subtend when viewed from the satellite?
4.31 If the Earth radiates as a blackbody at an
equivalent blackbody temperature T
E
255 K,
calculate the radiative equilibrium temperature
of the satellite when it is in the Earth’s shadow.
[Hint: Let dE be the amount of radiation flux
imparted to the satellite by the flux density dE
received within the infinitesimal element of
solid angle d
.] Then,
where r is the radius of the satellite and I is the
intensity of the radiation emitted by the Earth,
i.e., the flux density of blackbody radiation, as
given by (4.12), divided by
. Integrate the
above expression over the arc of solid angle
subtended by the Earth, as computed in the
previous exercise, noting that the radiation is
isotropic, to obtain the total energy absorbed
by the satellite per unit time
Finally, show that the temperature of the
satellite is given by
Q 2.21r
2
T
4
E
dE
r
2
Id
4.32 Show that the approach in Exercise 4.5 in the
text, when applied to the previous exercise,
yields a temperature of
Explain why this approach underestimates the
temperature of the satellite. Show that the
answer obtained with this approach converges
to the exact solution in the previous exercise as
the distance between the satellite and the center
of the Earth becomes large in comparison to the
radius of the Earth R
E
.[Hint: show that as
, the arc of solid angle subtended by
the Earth approaches .]
4.33 Calculate the radiative equilibrium temperature
of the satellite immediately after it emerges
from the Earth’s shadow (i.e., when the satellite
is sunlit but the Earth, as viewed from the
satellite, is still entirely in shadow).
4.34 The satellite has a mass of 100 kg, a radius of 1
m, and a specific heat of 10
3
J kg
1
K
1
.
Calculate the rate at which the satellite heats up
immediately after it (instantaneously) emerges
from the Earth’s shadow.
4.35 Consider two opaque walls facing one another.
One of the walls is a blackbody and the other
wall is “gray” (i.e.,
independent of
).The
walls are initially at the same temperature T and,
apart from the exchange of radiation between
them, they are thermally insulated from their
surroundings. If
and
are the absorptivity and
emissivity of the gray wall, prove that
.
Solution: The flux emitted by the black wall is
F
T
4
and the flux absorbed by the gray wall is
T
4
.The flux emitted by the gray wall is
T
4
.
The rate at which the gray wall gains or loses
energy from the exchange of radiation with the
black wall is
If H is not zero, then the temperature of the
wall must change in response to the energy
(
)
T
4
H
T
4
T
4
R
2
E
d
2
d
R
E
:
T
s
T
E
1
4
6371
8371
2
1
4
158 K
T
s
T
E
2.21
4
1
4
satellite
Earth
Fig. 4.37 Geometric setting for Exercises 4.30–4.34.
P732951-Ch04.qxd 12/16/05 11:04 AM Page 148

Exercises 149
imbalance, in which case, heat is being
transferred from a colder body to a warmer
body, in violation of the second law of
thermodynamics. It follows that
■
4.36 (a) Extend the proof in the previous exercise to
the case in which absorptivity and emissivity are
wavelength dependent. Let one of the walls be
black, as in the previous exercise, and let the
other wall also be black, except within a very
narrow wavelength range of width
, centered
at
1
where 1. [Hint: Because
blackbody radiation is isotropic, it follows the
blackbody flux in the interval
is
B(
1
, T)
. Using this relationship, consider the energy
balance as in the previous exercise and proceed
to show that .] (b) Indicate how this
result could be extended to prove that
4.37 Consider a closed spherical cavity in which the
walls are opaque and all at the same
temperature.The surfaces on the top hemisphere
are black and the surfaces on the bottom
hemisphere reflect all the incident radiation at
all angles. Prove that in all directions I
B
.
4.38 (a) Consider the situation described in
Exercise 4.35, except the both plates are gray,
one with absorptivity
1
and the other with
absorptivity
2
. Prove that
where and are the flux densities of the
radiation emitted from the two plates. Make use
of the fact that the two plates are in radiative
equilibrium at the same temperature but do not
make use of Kirchhoff’s law. [Hint: Consider the
total flux densities F
1
from plate 1 to plate 2 and
F
2
from plate 2 to plate 1.The problem can be
worked without dealing explicitly with the
multiple reflections between the plates.]
4.39 Consider the radiation balance of an
atmosphere with a large number of layers, each
of which is isothermal, transparent to solar
radiation, and absorbs the fraction
of the
F
2
F
1
F
1
1
F
2
2
1
1
a
1
longwave radiation incident on it from above or
below. (a) Show that the flux density of the
radiation emitted by the topmost layer is
F(2
) where F is the flux density of the
planetary radiation emitted to space. By
applying the Stefan–Boltzmann law (4.12) to an
infinitesimally thin topmost layer, show that the
radiative equilibrium temperature at the top of
the atmosphere, sometimes referred to as the
skin temperature, is given by
(Were it not for the presence of stratospheric
ozone, the temperature of the 20- to 80-km
layer in the Earth’s atmosphere would be close
to the skin temperature.)
4.40 Consider an idealized aerosol consisting of
spherical particles of radius r with a refractive
index of 1.5. Using Fig. 4.13, estimate the
smallest radius for which the particles would
impart a bluish cast to transmitted white light,
as in the rarely observed “blue moon.”
4.41 Consider an idealized cloud consisting of
spherical droplets with a uniform radius of 20
m and concentrations of 1 cm
3
. How long a
path through such a cloud would be required to
deplete a beam of visible radiation by a factor
of e due to scattering alone? (Assume that none
of the scattered radiation is subsequently
scattered back into the path of the beam.)
4.42 Consider solar radiation with a zenith angle of
0° that is incident on a layer of aerosols with a
single scattering albedo
0
0.85, an
asymmetry factor g 0.7, and an optical
thickness
0.1 averaged over the shortwave
part of the spectrum.The albedo of the
underlying surface is R
s
0.15.
(a) Estimate the fraction of the incident radiation
that is backscattered by the aerosol layer in its
downward passage through the atmosphere.
(b) Estimate the fraction of the incident
radiation that is absorbed by the aerosol
layer in its downward passage through the
atmosphere.
(c) Estimate the consequent corresponding
impact of the aerosol layer upon the local
albedo. Neglect multiple scattering. For
simplicity, assume that the radiation
T*
1
2
1
4
T
E
P732951-Ch04.qxd 12/16/05 11:04 AM Page 149

150 Radiative Transfer
back-scattered from the earth’s surface and
clouds is parallel beam and oriented at 0
or 180 Zenith angle. (In reality it is
isotropic.) [Hint: Show that the fraction of
the radiation that is backscattered in its
passage through the layer is
and the fraction that is transmitted through
the layer is
Then show that the total upward reflection
from the top of the atmosphere is
which can be rewritten in the form
4.43 Consider radiation with wavelength
and zero
zenith angle passing through a gas with an
absorption coefficient k
of 0.01 m
2
kg
1
.What
fraction of the beam is absorbed in passing
through a layer containing 1 kg m
2
of the gas?
What mass of gas would the layer have to contain
in order to absorb half the incident radiation?
4.44 Show that for overhead parallel beam radiation
incident on an isothermal atmosphere in which
the r, the mixing ratio of the absorbing gas, and
k
, the volume absorption coefficient, are both
independent of height, the strongest absorption
per unit volume (i.e., dI
dz) is strongest at the
level of unit optical depth.
Solution: From (4.17) if r and k
are both
independent of height,
(4.61)
where I
is the intensity of the radiation incident
on the top of the atmosphere, T
I
I
is the
transmissivity of the overlying layer, and
is the
density of the ambient air. From (4.33)
dI
dz
I
T
(k
r)
b
R
s
t
2
(1 bR
s
)
b R
s
t
2
(1 bR
s
b
2
R
2
s
)
t e
0
(1 e
)
(1
)
2
b
0
(1 e
)
(1
)
2
and from the hypsometric equation applied to
an isothermal layer
Substituting for T
and
in (4.61) we obtain
From (4.32)
(4.62)
Using (4.62) to express e
zH
in the
aforementioned equation in terms of optical
depth, we obtain
Now at the level where the absorption is
strongest,
Performing the indicated differentiation, we
obtain
from which it follows that
1. Although
this result is strictly applicable only to an
isothermal atmosphere in which k
and r are
independent of height, it is qualitatively
representative of conditions in planetary
atmospheres in which the mixing ratios of the
principal absorbing constituents do not change
rapidly with height. It was originally developed
by Chapman
28
for understanding radiative and
photochemical processes related to the
stratospheric ozone layer.
e
d
dz
(1
) 0
d
dz
dI
dz
I
H
d
dz
(
e
) 0
dI
dz
I
H
e
H(k
r
0
)e
z
H
(k
r
0
)
z
e
z
H
dz
dI
dz
I
(k
r
0
)e
z
H
e
0
e
z
H
T
e
P732951-Ch04.qxd 12/16/05 11:04 AM Page 150
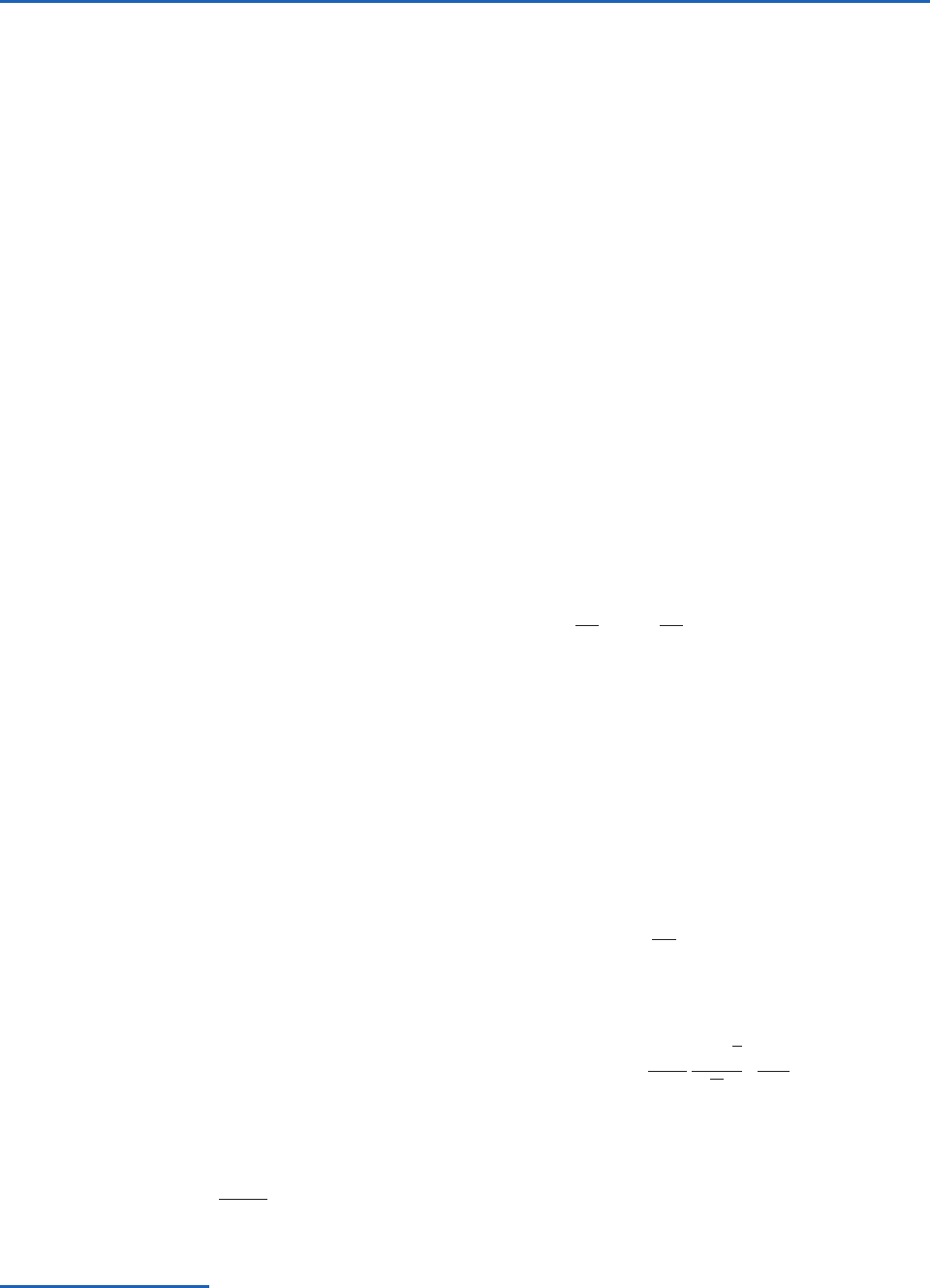
Exercises 151
4.45 For incident parallel beam solar radiation in an
isothermal atmosphere in which k
is
independent of height (a) show that optical
depth is linearly proportional to pressure and
(b) show that the absorption per unit mass (and
consequently the heating rate) is strongest, not
at the level of unit optical depth but near the
top of the atmosphere, where the incident
radiation is virtually undepleted.
4.46 Consider a hypothetical planetary atmosphere
comprised entirely of the gas in Exercise 4.43.
The atmospheric pressure at the surface of the
planet is 1000 hPa, the lapse rate is isothermal,
the scale height is 10 km, and the gravitational
acceleration is 10 m s
2
. Estimate the height and
pressure of the level of unit normal optical depth.
4.47 (a) What percentage of the incident
monochromatic intensity with wavelength
and zero zenith angle is absorbed in passing
through the layer of the atmosphere
extending from an optical depth
0.2 to
4.0?
(b) What percentage of the outgoing
monochromatic intensity to space with
wavelength
and zero zenith angle is
emitted from the layer of the atmosphere
extending from an optical depth
0.2 to
4.0?
(c) In an isothermal atmosphere, through how
many scale heights would the layer in (a)
and (b) extend?
4.48 For the atmosphere in Exercise 4.46, estimate
the levels and pressures of unit (slant path)
optical depth for downward parallel beam
radiation with zenith angles of 30° and 60°.
4.49 Prove that the optical thickness of a layer is
equal to (1) times the natural logarithm of
the transmissivity of the layer.
4.50 Prove that the fraction of the flux density of
overhead solar radiation that is backscattered
to space in its first encounter with a particle in
the atmosphere is given by
b
1
2
where
is the asymmetry factor defined
in (4.35). [Hint:The intensity of the scattered
radiation must be integrated over zenith
angle.]
4.51 Show that Schwarzschild’s equation in the form
that it appears in (4.41) in the text
can be integrated along a path extending from
0 to s
1
in Fig. 4.26 to obtain an expression for
I
(s
1
).
4.52 Prove that as the optical thickness of a layer
approaches zero, the flux transmissivity, as
defined in Eq. (4.45), becomes equal to the
intensity transmissivity at a zenith angle of
60 degrees.
4.53 Integrate the expression for the heating rate, as
approximated by cooling to space that appears
as Eq. (4.55) of the text, namely
(4.55)
over solid angle.
4.54 A thin, isothermal layer of air in thermal
equilibrium at temperature T
0
is perturbed
about that equilibrium value (e.g., by absorption
of a burst of ultraviolet radiation emitted by the
sun during a short-lived solar flare) by the
temperature increment
T. Using the cooling to
space approximation (4.56) show that
(4.63)
where
(4.64)
This formulation, in which cooling to space acts
to bring the temperature back toward radiative
equilibrium, is known as Newtonian cooling or
radiative relaxation. It is widely used in
k
r
c
p
e
dB
dT
T
0
dT
dt
T
dT
dt
2
c
p
1
0
k
rB
(z)e
d
dI
(I
B
(T ))k
rds
28
Sydney Chapman (1888–1970) English geophysicist. Made important contributions to a wide range of geophysical problems, includ-
ing geomagnetism, space physics, photochemistry, and diffusion and convection in the atmosphere.
P732951-Ch04.qxd 12/16/05 11:04 AM Page 151

152 Radiative Transfer
parameterizing the effects of longwave radiative
transfer in the middle atmosphere.
4.55 Prove that weighting function w
i
used in remote
sensing, as defined in (4.59), can also be
expressed as the vertical derivative of the
transmittance of the overlying layer.
4.56 The annual mean surface air temperature
ranges from roughly 23 °C in the tropics to
25 °C in the polar cap regions. On the basis
of the Stefan–Boltzmann law, estimate the
ratio of the flux density of the emitted
longwave radiation in the tropics to that in the
polar cap region.
P732951-Ch04.qxd 12/16/05 11:04 AM Page 152

Atmospheric chemistry studies were originally
concerned with determining the major gases in the
Earth’s atmosphere. In the latter half of the last
century, as air pollution became an increasing
problem in many large cities, attention turned to
identifying the sources, properties, and effects of the
myriad of chemical species that exist in the natural
and polluted atmosphere. Acid deposition, which
became recognized as a widespread problem in the
1970s, led to the realization that chemical species
emitted into the atmosphere can be transported
over large distances and undergo significant trans-
formations as they move along their trajectories.
The identification in 1985 of significant depletion of
ozone in the Antarctic stratosphere focused atten-
tion on stratospheric chemistry and the susceptibility
of the stratosphere to modification. More recently,
studies of the effects of trace chemical constituents
in the atmosphere on the climate of the Earth have
moved to center stage.
The focus of this chapter is on some of the basic
concepts and principles underlying atmospheric chem-
istry, as illustrated by the effects of both natural and
anthropogenic trace constituents. For the most part,
we confine our attention in this chapter to gas-phase
chemistry and atmospheric aerosols. The interactions
of gases and aerosols with tropospheric clouds are
discussed in Chapter 6.
5.1 Composition of
Tropospheric Air
The ancient Greeks considered air to be one of the four
“elements” (the others being earth, fire and water).
Leonardo da Vinci,
2
and later Mayow,
3
suggested that
air is a mixture consisting of one component that sup-
ports combustion and life (“fire-air”) and the other
that does not (“foul-air”). “Fire-air” was isolated by
Scheele
4
in 1773 and independently by Priestley
5
153
Atmospheric Chemistry
1
5
1
This chapter is based in part on P. V. Hobbs’ Introduction to Atmospheric Chemistry, Cambridge University Press, New York, 2000, to
which the reader is referred for more details on atmospheric chemistry. If the reader feels a need for a review of the basic principles of
chemistry, this is given in P. V. Hobbs’ Basic Physical Chemistry for the Atmospheric Sciences, 2nd Edition, Cambridge University Press,
New York, 2000. Both of these books are designed for upper-class undergraduate and first-year graduate students and, like the present
book, contain numerous worked exercises and exercises for the student.
2
Leonardo da Vinci (1452–1519) Renowned Italian painter, architect, engineer, mathematician, and scientist. Best known for his
paintings (e.g., the Mona Lisa, the Last Supper). His notebooks reveal his knowledge of human anatomy and natural laws, as well as his
mechanical inventiveness.
3
John Mayow (1640–1679) English chemist and physiologist. Described the muscular actions around the chest involved in respiration.
4
Carl Wilhelm Scheele (1742–1786) Swedish chemist. Discoverer of many chemicals, including oxygen, nitrogen, chlorine, manganese,
hydrogen cyanide, citric acid, hydrogen sulfide, and hydrogen fluoride. Discovered a process similar to pasteurization.
5
Joseph Priestley (1733–1804) English “tinkerer” par excellence. Never took a formal science course. Discovered that graphite
(i.e., carbon) can conduct electricity (carbon is the main ingredient in modern electrical circuitry), the respiration of plants (i.e., they take
in carbon dioxide and release oxygen), and he isolated photosynthesis, and isolated nitrous oxide, N
2
O (“laughing gas”—later to become
the first surgical anesthetic), ammonia (NH
3
), sulfur dioxide (SO
2
), hydrogen sulfide (H
2
S), and carbon monoxide (CO). Also discovered
that India gum can be used to rub out lead pencil marks. Due to his support of both the American and the French Revolution, his home
and church in England were burned down by a mob. Emigrated to the United States in 1794.
P732951-Ch05.qxd 12/09/2005 09:05 PM Page 153
