Водопьян Г.М., Уваров А.Ю. О построении модели процесса информатизации школы

Подождите немного. Документ загружается.

Глава 3. Использование К;модели для классификации школ

113311

Проверка на контрольной выборке. Чтобы проверить результаты клас%

теризации на контрольной выборке школ, мы включили в эксперимен%

тальную выборку шесть школ, которые входят в сеть ОРТа и состояние

процессов информатизации в которых хорошо знакомо авторам.

Как и ожидалось, школы № 1299 (Москва) и № 550 (Санкт%Петербург)

образовали отдельные кластеры. Обе эти школы являются безусловными

лидерами в области информатизации среди школ контрольной группы и

заметно отличаются от всех прочих школ по истории информатизации и

практике внедрения ИКТ в учебный процесс. В один кластер попали

школа № 42 (Самара), технологический лицей (Кишинев, Молдавия) и

частно%государственная школа (Бишкек, Киргизия). Это хорошо согла%

суется с данными других источников: все эти школы оснащались сред%

ствами ИКТ по общему стандарту, и процесс информатизации в них идет

по аналогичным программам. Как и предполагалось, в один кластер попа%

ли киевский технологический лицей ОРТ и школа № 1311. По мнению

экспертов ОРТа, данные школы по состоянию информатизации схожи.

Таким образом, проверка на контрольной выборке показала довольно точ%

ное соответствие результатов кластеризации с реальным положением дел

в этих школах.

Оценка устойчивости выявленной кластерной структуры. Устойчи%

вость кластерной структуры — один из показателей достоверности полу%

ченной классификации. Данный показатель особенно важен тогда, когда

классификация проводится на относительно небольшой выборке объек%

тов [8, с. 160]. Мы проверили влияние «выбросов» на результаты клас%

теризации. Из выборки были исключены школы № 1299 и № 550 с кодами

№№ 8 и 94 (табл. 15), которые образовывали отдельные кластеры. Клас%

сификация оставшихся объектов не изменилась. Это позволяет утвер%

ждать, что полученная кластерная структура устойчива к выбросам.

Таким образом, мы убедились, что результаты кластеризации школ мето%

дом Уорда дают достаточно правдоподобное распределения школ по клас%

терам. Косвенным подтверждением значимости полученного разбиения

школ на кластеры служат и результаты дискриминантного анализа, кото%

рый позволяет правильно классифицировать около 96% школ, участво%

вавших в кластеризации.

Еще один важный признак хорошей кластеризации — возможность содер%

жательной интерпретации полученной кластерной структуры (см. далее

раздел «Обсуждение результатов кластеризации»).

O postroenii_verstka4.qxd 17.07.2006 15:55 Page 131

Глава 3. Использование К;модели для классификации школ

113322

ООппррееддееллееннииее ммеессттаа ооббррааззооввааттееллььннооггоо ууччрреежжддеенниияя

вв ппррооссттррааннссттввее ииннффооррммааттииззааццииии

Итак, мы получили искомую классификацию школ. Теперь нам нужна

процедура, чтобы определить:

• какая из школ каждого кластера является наиболее типичной (фо%

кусной школой);

• к какому из выделенных кластеров принадлежит новая произволь%

но выбранная школа.

Для этого мы использовали дискриминантный анализ. Он позволяет:

• вычислить для каждой школы экспериментальной выборки значе%

ния дискриминирующих функций и на этой основе определить

удаленность классифицируемых объектов от центроида соответ%

ствующей группы (найти фокусные школы);

• построить для каждого кластера классифицирующую функцию и

с ее помощью по данным, содержащимся в анкете новой школы,

найти, к какому из кластеров эта школа относится.

Чтобы построить дискриминирующие функции, необходимо:

• преобразовать данные новой школы к нормальному виду, исполь%

зуя средние значения и стандартные отклонения переменных, ко%

торые описывают школы экспериментальной выборки;

• определить для этой новой школы значения параметров кластери%

зации (факторов) с помощью коэффициентов, которые получены

в результате регрессионного анализа;

• провести дискриминантный анализ школ экспериментальной вы%

борки, к которой добавлена эта новая школа.

Мы выбрали в качестве дискриминантных переменных параметры клас%

теризации (факторы), а в качестве классифицирующей переменной — но%

мер кластера. В нашем случае это 8 факторов и 11 кластеров. Для дискри%

минации был выбран метод под названием «Одновременный учет всех

независимых переменных».

Каноническая дискриминирующая функция является линейной комби%

нацией дискриминантных переменных для каждого объекта в группе [8].

В нашем случае она имеет вид

= u

+ u

1km

+ u

2km

+ ... + u

8km

где f

— значение канонической дискриминирующей функции для

m*го объекта (школы) выборки в кластере k;

O postroenii_verstka4.qxd 17.07.2006 15:55 Page 132

Глава 3. Использование К;модели для классификации школ

113333

ikm

— значение дискриминантной переменной (в нашем случае — фак%

тора) F

, i = 1, ... , 8 для m%го объекта (школы) в кластере k;

— коэффициенты дискриминирующих функций, которые обеспечи%

вают выполнение требуемых условий.

Коэффициенты u

выбираются таким образом, чтобы их средние значения

для разных кластеров как можно больше отличались друг от друга, а сами

функции не коррелировали друг с другом. Процедура выбора похожа на

поиск новых осей в пространстве классификации, проекции на которые

средних точек кластеров максимально различны.

Согласно теории, максимальное количество канонических дискримини%

рующих функций меньше любого из двух чисел: количества групп минус

единица и количества дискриминантных переменных. Поиск коэффициен%

тов дискриминирующих функций сводится к решению системы линейных

уравнений. В результате, для каждой функции получают набор коэффи%

циентов u

и характерное для каждой функции собственное значение,

величина которого описывает так называемую дискриминирующую способ%

ность (или дискриминантную полезность) функции: чем больше собствен%

ное значение, тем больше групп (кластеров) разделяет соответствующая

функция. Таким образом, функция с наибольшим собственным значением

является и самым мощным дискриминатором, а функция с наименьшим

собственным значением — самым слабым дискриминатором. Если имеет%

ся более одной функции, то собственному значению каждой функции

приписывается процентное содержание от суммы собственных значений

всех функций, и на основе этого значения судят об ее дискриминирующей

способности.

Формальное решение нашей задачи состоит из восьми дискриминирую%

щих функций, так как все они имеют собственные значения больше еди%

ницы. Некоторые из них могут оказаться статистически малозначимыми.

Оценить реальную (абсолютную) значимость найденных функций только

на основе собственных чисел невозможно. Поэтому для оценки реальной

дискриминирующей способности функций мы, кроме их собственных

значений, использовали два дополнительных теста: %статистики Уилкса

и коэффициенты канонической корреляции. Тройная проверка позволяет

в максимальной степени гарантировать себя от ошибок.

статистики Уилкса. Этот тест — общепринятая мера различения меж%

ду кластерами по нескольким дискриминантным переменным. Если вели%

чины близки к нулю, данные имеют высокий уровень различения: центро%

иды кластеров полностью разделены и сильно отличаются друг от друга.

O postroenii_verstka4.qxd 17.07.2006 15:55 Page 133

Глава 3. Использование К;модели для классификации школ

113344

Увеличение до максимального значения, равного единице, говорит об

ухудшении различения: центроиды кластеров совпадают (групповые раз%

личия отсутствуют). Данный тест еще до нахождения дискриминирую%

щей функции позволяет на основе %статистики определить, есть ли зна%

чимые различия между кластерами, или их нет.

Существенный недостаток %статистики для нашей задачи состоял в том,

что для вычисления с его помощью значимости остаточной дискримини%

рующей способности важно предположение о нормальности распреде%

ления выборки.

Табл. 18. Результаты теста для дискриминирующих функций

Количество Значимость остаточной

дискриминирующих статистика дискриминирующей

функций способности

0 0,000 0,001

1 0,001 0,001

2 0,008 0,001

3 0,027 0,001

4 0,093 0,001

5 0,234 0,001

6 0,469 0,001

7 0,758 0,001

Результаты теста для дискриминирующих функций представлены в табл.

18. После вычисления семи функций %статистика равна 0,758, значи%

мость остаточной дискриминирующей способности составляет 0,001.

Полученный уровень значимости показывает, что ситуация, при которой

между центроидами кластеров нет различий, может случиться не чаще,

чем в одной из тысячи случайных выборок. Это событие маловероятно.

Таким образом, все семь функций являются статистически значимыми, но

для описания всей совокупности имеющихся данных их недостаточно —

нужны все восемь функций.

То же можно сказать и о дискриминантных переменных. Как видно из

табл. 19, по средним значениям восьми переменных кластеры различают%

ся на уровне значимости остаточной дискриминирующей способности

менее 0,001. Следовательно, надо использовать все восемь переменных.

O postroenii_verstka4.qxd 17.07.2006 15:55 Page 134

Табл. 19. Результаты теста для дискриминантных переменных

Значимость остаточной

Дискриминантные статистика дискриминирующей

переменные способности

1 0,308 0,000

2 0,115 0,000

3 0,284 0,000

4 0,362 0,000

5 0,541 0,000

6 0,419 0,000

7 0,549 0,000

8 0,494 0,000

Коэффициенты канонической корреляции. Реальной оценкой полезности

дискриминирующей функции является коэффициент канонической

корреляции, который характеризует влияние этой функции на отнесение

классифицируемого объекта к тому или иному кластеру.

В табл. 20 приведены собственные значения и коэффициенты каноничес%

кой корреляции, рассчитанные для наших данных. Видно, что наибольший

интерес для нас представляют первые шесть функций. Но седьмая и вось%

мая функции, судя по величине коэффициентов канонической корреляции,

все%таки обладают заметной дискриминирующей способностью, и их нельзя

игнорировать. Таким образом, для решения нашей задачи необходимы все

восемь дискриминирующих функций.

Табл. 20. Собственные значения и коэффициенты канонической корреляции

Дискримини Накопленная Коэффициент

рующие Собственное Объясненная объясненная канонической

функции значение дисперсия дисперсия корреляции

1 16,653 55,8 55,8 0,971

2 4,678 15,7 71,5 0,908

3 2,620 8,8 80,3 0,851

4 2,405 8,1 88,4 0,840

5 1,529 5,1 93,5 0,778

6 1,001 3,4 96,8 0,707

7 0,621 2,1 98,9 0,619

8 0,320 1,1 100,0 0,492

Глава 3. Использование К;модели для классификации школ

113355

O postroenii_verstka4.qxd 17.07.2006 15:55 Page 135

Глава 3. Использование К;модели для классификации школ

113366

Суммируя результаты, которые представлены в таблицах 18—20, можно

сказать, что в нашем случае необходимо проводить дискриминантный

анализ по восьми дискриминантным переменным и найти восемь дискри%

минирующих функций.

ВВыыббоорр ффооккуусснныыхх шшккоолл

Одной из важных составляющих К%модели являются фокусные школы —

типичные (с точки зрения состояния информатизации) представители

своего кластера, по которым можно с достаточной долей определенности

судить о других школах, вошедших в данный кластер. Фокусные школы

определялись следующим образом.

Сначала исследовалась однородность кластера с помощью диаграммы

рассеяния. На ее осях отложены значения дискриминирующих функций,

которые обладают наибольшей дискриминирующей способностью. К со%

жалению, анализ распределения школ в восьмимерном пространстве с по%

мощью диаграмм затруднен и носит во многом эвристический характер.

Потом анализировались расстояния между центром кластера и школами,

которые его образуют. Для однородного кластера формальное требование

к фокусной школе — расположение в его центре. Соответственно, чтобы

выявить фокусные школы, в каждом кластере вычислялись средние зна%

чения факторов, задающие его центр, и евклидово расстояние между

центром кластера и координатами входящих в него школ. Школы, у кото%

рых это расстояние было наименьшим, претендовали на роль фокусных.

Данный признак подходит для маленьких кластеров (№№ 9—11). Он яв%

ляется доминирующим и для однородных кластеров (№№ 1, 3 и 7). Если

кластер неоднороден (№№ 2, 4, 5, 6 и 8), то выбор фокусной школы

существенно зависит от его структуры. Но в общем случае надо подходить

к выделению фокусных школ прагматически и руководствоваться прежде

всего тем, как будут использоваться подготавливаемые в этих школах

Истории информатизации. Очевидно, что для многих целей полезно учи%

тывать при выборе фокусных школ их тип или местоположение (например,

выделять сельские малокомплектные школы).

Выбор претендентов на роль фокусной школы мы приводили в процессе

анализа результатов кластеризации.

O postroenii_verstka4.qxd 17.07.2006 15:55 Page 136

Глава 3. Использование К;модели для классификации школ

113377

ООппррееддееллееннииее ккллаассттеерраа ддлляя ппррооииззввооллььнноо ввыыббрраанннноойй шшккооллыы

Чтобы определить к которому из кластеров принадлежит школа, не вхо%

дившая в первичную выборку, необходимо знать классифицирующую

функцию для каждого кластера. Простая классифицирующая функция

для кластера k является линейной комбинацией дискриминантных

переменных и относится ко всему классу в целом:

= b

+ b

+ ... + b

где X

— дискриминантные переменные,

— коэффициенты, которые необходимо определить.

В связи с тем, что объект будет отнесен к классу с наибольшим значением

классифицирующей функции, точные значения функции особой роли

не играют.

Табл. 21. Коэффициенты классифицирующих функций (b

)

Дискриминантные Кластеры (k)

переменные (j) 123 4 5 6 7 8 9 10 11

1 %4,17 %3,04 %1,18 2,56 3,30 %1,97 0,56 2,54 8,48 48,95 16,64

2 1,76 %4,09 %1,87 %2,54 %8,68 %3,82 %3,90 5,03 17,38 124,22 19,64

3 %2,61 1,68 %3,45 %2,88 4,20 %0,75 2,72 7,19 6,18 %2,84 19,41

4 0,27 4,36 0,29 0,01 4,27 1,06 2,30 %5,18 %16,00 %27,23 %15,29

5 %0,59 %3,28 0,02 %0,39 0,87 1,74 2,19 %3,08 %2,44 %5,80 %4,84

6 %3,61 %1,17 %2,56 2,22 %1,39 2,86 2,25 0,68 1,94 1,34 7,02

7 0,50 0,90 %0,39 %2,96 2,60 %0,98 2,18 %3,24 %1,27 7,52 5,31

8 0,54 %1,16 0,30 %0,07 %1,26 3,28 %1,97 %2,33 4,34 %10,63 %11,84

0* %6,91 %9,52 %4,78 %8,22 %16,01 %5,97 %6,69 %14,54 %45,08 %606,23 %94,00

* % постоянный член классифицирующей функции H

Используя в качестве дискриминантных переменных восемь факторов,

мы получили для каждого кластера свою классифицирующую функцию,

которая задана коэффициентами b

(табл. 21). Эти коэффициенты позво%

ляют определить, к какому кластеру относится исследуемая школа.

O postroenii_verstka4.qxd 17.07.2006 15:55 Page 137

Глава 3. Использование К;модели для классификации школ

113388

Заметим, что школа может принадлежать более чем к одному кластеру

(например, если она находится на большом расстоянии от всех известных

кластеров либо на границе, то есть в зоне перекрытия двух соседних клас%

теров). Тогда необходимо оценить вероятность ее принадлежности к каж%

дому из этих кластеров (это можно сделать с помощью пакета программ

SPSS) и затем уже решить, к какому из них она относится. Однако в на%

шем случае предпочтительнее принимать решение с учетом мнения экс%

пертов — ведь процедура вычисления вероятностей основана на предпо%

ложении, что используемые распределения подчиняются нормальному

закону, а этого нельзя гарантировать.

Для оценки точности процедуры классификации мы применили ее к шко%

лам экспериментальной выборки, кластерная принадлежность которых

нам была известна. Расчеты показали, что 95,7% школ, входящих в эту

выборку, были классифицированы правильно. Четыре школы (или 4, 3%)

оказались в зоне перекрытия двух соседних кластеров.

O postroenii_verstka4.qxd 17.07.2006 15:55 Page 138

Глава 4. Обсуждение результатов кластеризации

113399

ГГллаавваа 44

ООББССУУЖЖДДЕЕННИИЕЕ РРЕЕЗЗУУЛЛЬЬТТААТТООВВ ККЛЛААССТТЕЕРРИИЗЗААЦЦИИИИ

Главное свойство хорошей классификации — возможность содержательной

интерпретации полученной кластерной структуры. Самый простой спо%

соб такой интерпретации — обратиться к Историям информатизации и

выделить общее/различное для школ, попавших в одинаковые классифи%

кационные группы. Однако мы пока лишены этой возможности. Еще

один способ — обратиться к интерпретации по кластерным профилям,

которая широко применяется в кластерном анализе. Мы воспользовались

одним из вариантов такой интерпретации, в ходе которой профили

строятся на основе описательных статистик для каждого фактора.

ХХааррааккттееррииссттииккии рраассппррееддееллеенниияя ффааккттооррнныыхх ззннааччеенниийй

Прежде чем проводить интерпретацию по кластерным средним, следует

убедиться, что имеющиеся в нашем распоряжении значения параметров

кластеризации (факторов) подчиняются закону нормального распреде%

ления и можно использовать соответствующие математические модели.

Для этого мы провели исследование этих распределений: вычислили де%

скриптивные статистики (табл. 22), построили их гистограммы (рисунки

20—22) и проверили гипотезу об их нормальном распределении с помо%

щью теста Колмогорова%Смирнова (табл. 23).

Табл. 22. Дескриптивные статистики

Факторы

123 45678

Размер выборки 94 94 94 94 94 94 94 94

Среднее 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00

Стандартная ошибка среднего 0,10 0,09 0,10 0,09 0,10 0,10 0,09 0,10

Медиана %0,15 %0,10 0,03 %0,08 %0,35 %0,07 %0,12 %0,25

Мода %0,71 %1,54 %1,82 %1,51 %1,48 %1,71 %1,99 %1,60

Стандартное отклонение 1,00 0,89 0,93 0,88 0,97 0,99 0,87 0,95

Дисперсия 0,99 0,79 0,87 0,77 0,93 0,98 0,77 0,91

Коэффициент асимметрии 7,93 0,27 %0,03 0,91 1,20 0,59 1,12 2,00

Ошибка коэффициента

асимметрии 0,25 0,25 0,25 0,25 0,25 0,25 0,25 0,25

O postroenii_verstka4.qxd 17.07.2006 15:55 Page 139

Глава 4. Обсуждение результатов кластеризации

114400

Эксцесс 70,83 %0,89 %0,76 1,29 0,86 0,11 3,10 4,67

Ошибка эксцесса 0,49 0,49 0,49 0,49 0,49 0,49 0,49 0,49

Диапазон 9,65 3,31 3,79 4,84 4,48 4,61 5,57 5,10

Минимум %0,71 %1,54 %1,82 %1,51 %1,48 %1,71 %1,99 %1,60

Максимум 8,93 1,77 1,97 3,33 3,00 2,90 3,58 3,50

Процентили %0,30 %0,74 %0,65 %0,63 %0,60 %0,95 %0,46 %0,51

%0,15 %0,10 0,03 %0,08 %0,35 %0,07 %0,12 %0,25

0,00 0,72 0,68 0,43 0,45 0,47 0,37 0,10

Табл. 23. Тест КолмогороваСмирнова на нормальность распределения

Факторы

123 45678

Критерий

Колмогорова%Смирнова 2,814 0,774 0,566 1,072 2,031 0,838 1,187 2,208

Вычисленный уровень

значимости 0,000 0,587 0,906 0,201 0,001 0,483 0,120 0,000

Мы обнаружили, что по своим статистическим характеристикам все пара%

метры (факторы) можно разделить на три группы.

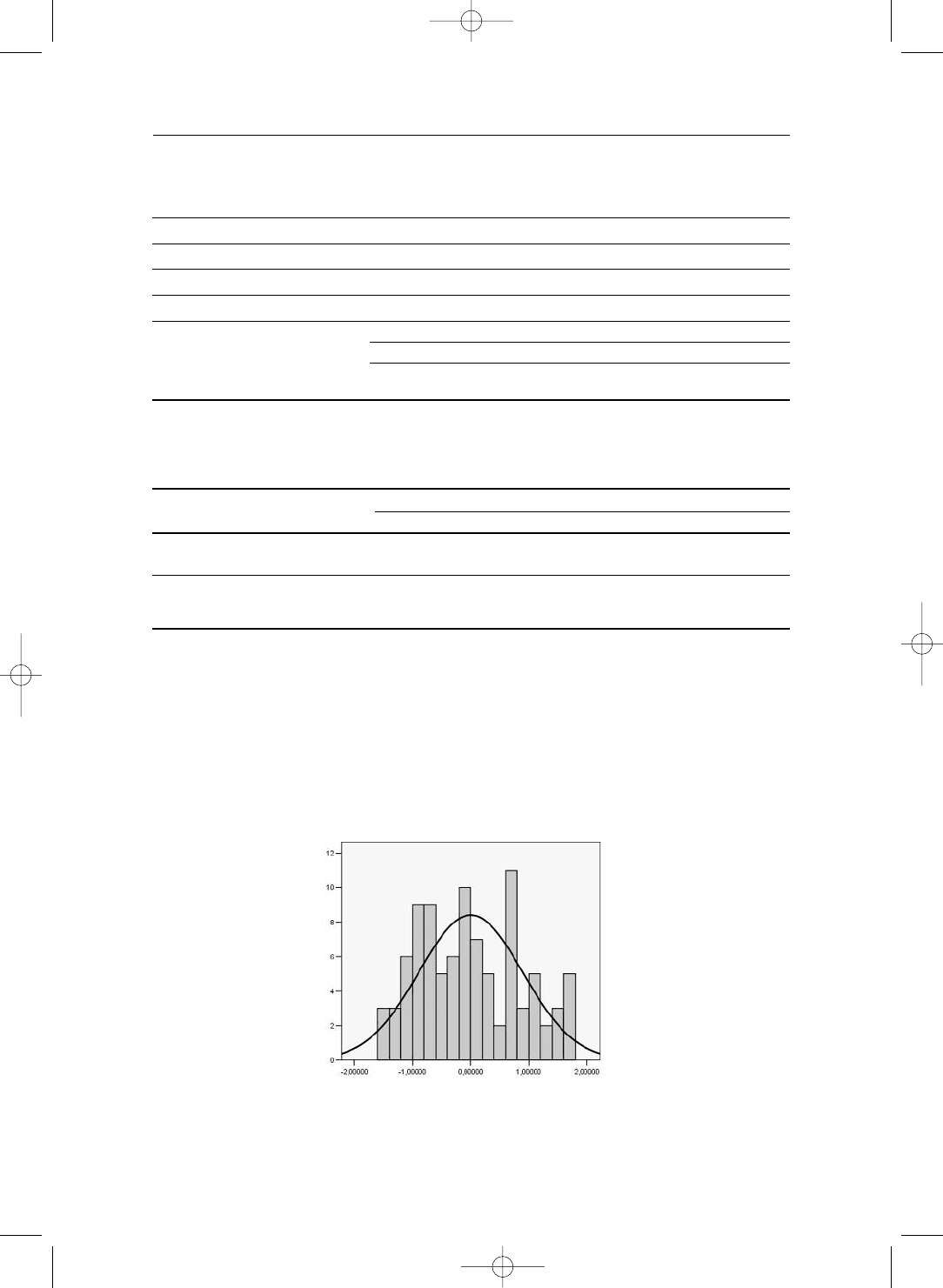
В первую группу вошли факторы №№ 2, 3 и 6, которые на уровне значи%

мости 0,01 можно считать нормально распределенными (рис. 20).

ФФааккттоорр 22

ффааккттоорр

ччаассттооттаа

O postroenii_verstka4.qxd 17.07.2006 15:55 Page 140