Venables J. Introduction to Surface and Thin Film Processes

Подождите немного. Документ загружается.

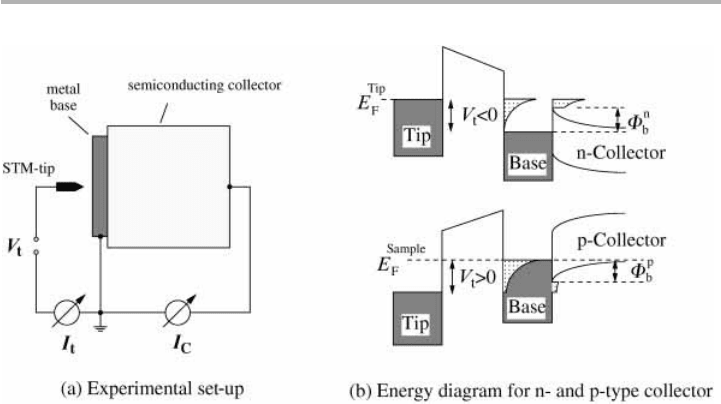
arrangement is shown in ﬁgure 8.6. BEEM can be understood as a hot electron triode,

in which the tunneling current (I

) into the metal serves as the source for the collected

current (I

) in the semiconductor. BEEM images can then be obtained by scanning the

tip, and compared with STM images of the same area, as shown for a thin metallic

CoSi

layer on Si(111) by von Känel et al. (1995). The application of STM and BEEM

to study silicides is reviewed by Bennett & von Känel (1999).

The corresponding spectroscopy (BEES) is possible, also spatially resolved at the

nanometer scale, and has become a very powerful means of determining local values

of the Schottky barrier height, as indicated in ﬁgure 8.7. Here I

is plotted against the

tip voltage V

for constant I

, and goes to zero as 2V

approaches

. These

values

are at least as good as those produced by large area electrical methods: a quite remark-

able achievement (Meyer & von Känel (1997).

It is a current research topic to understand the contrast mechanisms in both the

microscopy and spectroscopy. If the metal base electrode is featureless on the lateral

scale of interest, then BEEM contrast is thought to arise largely through eﬀects occur-

ring at the metal–semiconductor interface, though diﬀerences in experimental arrange-

ments may have lead to inconsistencies between diﬀerent groups. It is notable that

transmission through the base layer as a function of thickness oﬀers a direct measure-

ment of the inelastic mean free path (imfp) for low energy electrons, well below the

minimum in the imfp curves discussed earlier in section 3.3.4. For example, Ventrice et

al. (1996) show that for Au ﬁlms on Si(100) had

⬃ 13 nm at room temperature and

15 nm at 77 K, for an injected energy of around 1 eV above the Fermi level. It is thus

reasonable to use base electrodes with thickness up to tens of nanometers in these

techniques.

8.1 Metals and oxides in contact with semiconductors 267

Figure 8.6. (a) Schematic set-up of a BEEM experiment, indicating tunneling and collector

currents I

and I

and the tip voltage V

; (b) energy level diagrams for forward BEEM at an

n-type (top) and p-type collector (bottom) (after von Känel et al. 1995, reproduced with

permission).

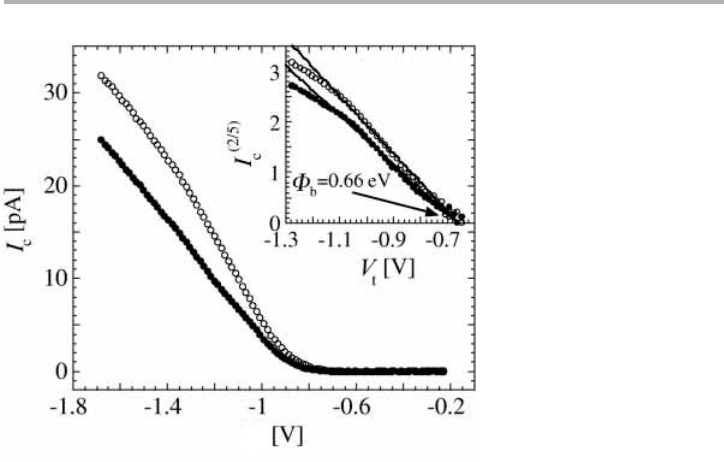
One of the possibilities of BEEM is to identify the defects responsible for surface

states. The images of misﬁt dislocations in the CoSi

/Si(111) interface can be seen at

high resolution to consist of a ‘string of pearls’ as shown in ﬁgure 8.8(b), rather than

a continuous line image which one might expect from a dislocation line. In the same

images there are also isolated point defects in the vicinity of the interface, and a sensi-

tivity of below 10

is claimed (Meyer & von Känel, 1997); the hypothesis is that

it is point defects trapped in the vicinity of dislocations, rather than the dislocations

themselves, which are electrically active.

This sensitivity level is particularly inviting in relation to the SiO

/Si and related

interfaces. One of the main reasons why the various MOS and CMOS silicon device

technologies work is the low density of surface states at the Si-SiO

interface, where

values below 10

(i.e. ⬃ 10

ML, or 10

on 1 mm

, or 10

on 1 mm

), can be con-

sistently achieved. However, it is extremely diﬃcult to deduce what these defects actu-

ally are; the technologist is primarily interested in getting rid of them, and often the

only means of assessing them are the same electrical properties which one is trying to

optimize: a sure recipe for a black art.

Recently, it has been shown that BEEM can address such problems. Using a base

electrode of thin granular Pt, electrons can be injected into, and can be trapped in, a

25 nm thick insulating ﬁlm of SiO

on Si. Trapping of very few (⬃ 10) electrons results

in a decrease of the BEEM current which can then be readily measured (Kaczer et al.

1996). A complementary (broad area) tool is electron spin resonance (ESR), which is

268 8 Surface processes in thin ﬁlm devices

Figure 8.7. Ballistic electron emission spectra I

) normalized to the tunneling current, taken

on top of (open circles) or next to (ﬁlled circles) an interfacial point defect. I

is higher on the

defect for V

close to the barrier height

. The inset shows the 2/5 power of I

, yielding a

value of

50.66 6 0.01 eV (after Meyer & von Känel 1997, reproduced with permisison).

very good for detecting unpaired electrons; these are typically the centers which give

rise to electron traps in SiO

, some of which are indicated in ﬁgure 8.9. These centers,

for example the P

center, which is an electron trapped on a Si dangling bond, are diﬀer-

ent in detail on surfaces of diﬀerent orientation (Helms & Poindexter, 1994). Another

sensitive wide beam technique is called Total reﬂection X-ray Fluorescence (TXRF),

which, by using glancing incidence X-rays, can detect below 10

(cm

) metal atoms on

ﬂat surfaces. It is now highly valued for examining the cleanliness of silicon wafers in

production plant environments (Schroder 1998, section 10.4).

8.1 Metals and oxides in contact with semiconductors 269

Figure 8.8. (a) STM topography image of a 2.8 nm thick CoSi

ﬁlm on Si(111), showing a

0.06 nm high line due to the strain ﬁeld of an interface dislocation (dashed line);

(b) corresponding BEEM image showing interfacial point defects, S and P, and those trapped

in the core of the interface dislocation D, which comprises empty (E) and occupied (O) regions

(after Meyer & von Känel 1997, reproduced with permisison).

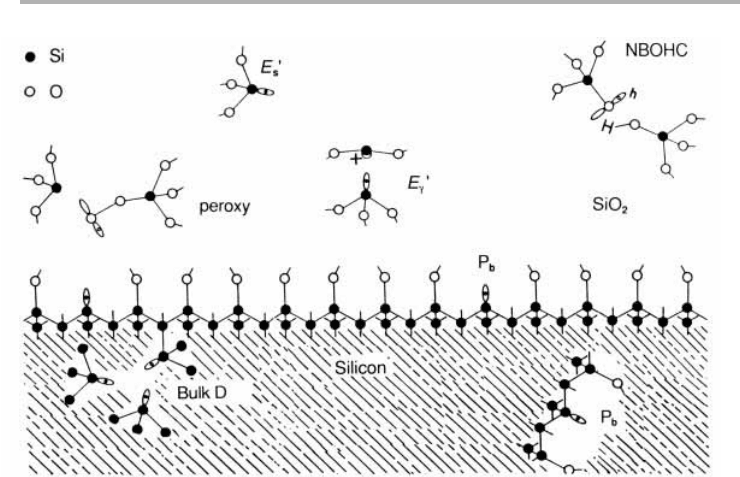
8.2 Semiconductor heterojunctions and devices

8.2.1 Origins of Schottky barrier heights

There has been much discussion of the origin of Schottky barrier heights, and other

related phenomena at metal–semiconductor and semiconductor–semiconductor inter-

faces. As often in physics, there are two limiting cases which can be addressed analyti-

cally, with reality either somewhere in between, or involving other elements not present

in either. The story starts with a half-page paper by Schottky (1938), and continues

with the opposing model of Bardeen (1947). The question to be answered is: what

determines the energy levels in the semiconductor?

In the Schottky model, we bring together the metal and the semiconductor, and

assume there is no electric ﬁeld in the space between them. This means that we can form

the barrier as the diﬀerence between the work function of the metal

, and the elec-

tron aﬃnity of the semiconductor

: i.e

. (8.7)

Equation (8.7) can be simply tested: pick any semiconductor, deposit a series of metals

on it, and measure the barrier height

. This should scale directly with the metal work

function

. The test has been done many times (see e.g. Brillson 1982, Rhoderick &

Williams, 1988 chapter 2, Lüth 1993/5 chapter 8) and the variation with metal work-

function is usually much weaker than this model implies. In the case of Mönch’s work

270 8 Surface processes in thin ﬁlm devices

Figure 8.9. Paramagnetic point defects which have been observed in SiO

/Si structures by

electron spin resonance. The NBOHC conﬁguration is the non-bridging-oxygen hole center

(after Helms & Poindexter 1994, reproduced with permission).

on Si(111)231 cited by Lüth, changing metals to give

varying from 2 to 5.5 eV

increases

modestly from 0.3 to 0.9 eV.

The opposite Bardeen model assumes that surface states are suﬃcient to pin the

Fermi level in the semiconductor, and notes that this energy level is placed at

above

the valence band edge. The top of the conduction band, which forms the barrier, is at

) above the Fermi level; thus

, (8.8)

and the barrier height shouldn’t vary at all with the work function of the metal. This

is also rarely satisﬁed in experiment, and we must consider that these two models con-

tinue to be discussed because they are simple limiting cases. Once one begins to think

in terms of the detailed mechanisms of what happens when two surfaces are put

together to form the interface, then the basis of both models falls apart. For example,

the two surfaces in vacuum may well be reconstructed, and this reconstruction will

change, and may be eliminated in the resulting metal–semiconductor interface. Also

the interfaces may well react chemically, and/or form a complex microstructure: do

such ‘metallurgical’ eﬀects have no inﬂuence on the result?

For many years these types of uncertainty lead to a whole series of tabulations of

data, and empirical models which were all more or less speciﬁc to particular systems.

This discussion was often played out at conferences, such as PCSI, Physics and

Chemistry of Semiconductor Interfaces, or ICFSI, International Conference on the

Formation of Semiconductor Interfaces, both still going at number 25 (January 1998,

published in J. Vac. Sci. Tech.) and number 6 (June 1997, published in Applied Surface

Science) respectively. Short of absorbing in detail a historical survey, such as those

written by Brillson (1982, 1992, 1994) or Henisch (1984), and to a lesser extent by

Rhoderick & Williams (1988) or Sutton & Balluﬃ (1995), the question for the ‘inter-

ested reader’ is: what can one extract of reasonable generality from this ﬁeld?

The model which has most appeal for me is that introduced in 1965 by Heine, and

developed by Flores & Tejedor (1979) and by Tersoﬀ (1984, 1985, 1986). There is also

an interestingly simple free electron model introduced by Jaros (1988). This topic is

reviewed by Tersoﬀ (1987) in the volume by Capasso & Margaritondo (1987), and by

Mönch (1993, 1994). Termed MIGS, this refers not to a Russian ﬁghter plane, but to

metal-induced gap states: i.e. to states which are present in the band gap of the semi-

conductor, and are populated due to the proximity of the metal. This leads to the result

that the Fermi level is pinned at an energy close to the middle of the gap, a similar result

to the Bardeen model, but for diﬀerent reasons. It further emphasizes the role of the

‘interface dipole’ and seeks to minimize this quantity. As such this becomes a (more or

less) quantitative statement of the underlying point that nature doesn’t like long range

ﬁelds, which I have been stressing from section 1.5 onwards. The bones of this argu-

ment are summarized without attribution in a useful introductory text by Jaros (1989).

The ingredients of this model can be seen in ﬁgure 8.10. We know that there are for-

bidden energy regions in a bulk semiconductor, with an energy gap of width E

. However, solution of the Schrödinger equation in a periodic potential does

not say that these gap states cannot exist, it merely says that they can’t propagate in an

8.2 Semiconductor heterojunctions and devices 271

inﬁnite medium. Mathematically this means that the k-vector has to have an imaginary

component iq, which ensures decay of the wavefunction; we have seen this as a condi-

tion for a surface state in section 1.5. This decay is slower nearer to the band edges, and

it is most rapid close to mid-gap.

Although this argument does depend in detail on the 3D reciprocal space geometry

of the particular crystal, the 1D model illustrated here, and worked through by Lüth

and by Mönch, gives the essential result. Thus the wavefunctions at these energies

decay into the semiconductor, and must be matched to the traveling-wave solutions in

the metal; this spill-over of charge creates an interface dipole, which is minimized if the

Fermi level is around mid-gap. We have already seen, in section 6.1, that an ML array

of relatively tiny electric dipoles can create quite large changes in electrostatic poten-

tial across the dipole sheet.

8.2.2 Semiconductor heterostructures and band offsets

The above points can be brought out even more forcefully by considering semiconduc-

tor heterostructures, as shown in ﬁgure 8.11. We bring together two semiconductors

and ask how the bands will line up. If the semiconductors are similar, but the align-

ment is as in ﬁgure 8.11(a), electrons will spill over from right to left; this creates, or is

the result of creating, a substantial interface dipole. However, in the more symmetric

alignment of diﬀerent semiconductors shown in ﬁgure 8.11(b), the electrons in the con-

duction band spill from right to left, whereas the sense is reversed in the valence band.

The resulting charge distribution is much more compensated, i.e. the interface dipole

is a lot smaller, and may even disappear. Simple, that’s the answer!

Considered in terms of the Fermi energy, this problem is rather diﬃcult to pose: we

want the Fermi levels to line up, but at low temperature there are no states at E

, so the

problem appears to be undeﬁned. In terms of the interface dipole, however, the

problem appears concrete, even if it is still just a bit elusive. As Tersoﬀ points out, if a

reference level can be found, then the problem is trivial, it has already been solved: this

272 8 Surface processes in thin ﬁlm devices

Figure 8.10. Elements of the MIGS model: (a) energy levels and wavefunction

(z) of states in

the gap close to a metal–semiconductor interface; (b) band diagram including the density of

states (DOS, dashed line) of the MIGS, which peak near the band edges. Note that the length

scale along z in panel (a) is much shorter than the scale d or L in ﬁgure 8.4, so that the bands

are shown to be only gently sloping (adapted from Lüth 1993/5).

(a)

z()

ψ( ) ~ ez

–qz

(b)

Valence

()

E k

E()

Conduction

DOS

is really what was going on in the Bardeen and Schottky models, but the reference levels

were assumed. Comparable models exist for semiconductor heterostructures. For

example the ionization potential model (often called the electron aﬃnity rule) is the

exact analogue of the Schottky model, where the vacuum potential is the reference

level, whereas the reference level in the case of metals is the Fermi energy. In Tersoﬀ’s

model, the reference point is the branching point energy E

, often called the charge

neutrality level, E

. It is diﬃcult to pin down the exact deﬁnition of this quantity, but

it corresponds to the energy where these states change over (branch) from being valence

band-like to conduction band-like, as in ﬁgure 8.10(b), and so usually the energy lies

near to mid-gap.

The electrostatic linear response model presented by Tersoﬀ is instructive, as it shows

why semiconductors are close to the metallic limit. In terms of a polarizability

, where

5«21, he ﬁnds that the valence band oﬀset (VBO) at the interface, DE

, is given by

/(11

)]DE

1[1/(11

)]DE

, (8.9)

where the ﬁrst quantity DE

is the diﬀerence between the charge neutrality levels, and

the second DE

is the diﬀerence between the ionization energy levels of the materials

in contact. Since for representative semiconductors,

⬃ 10, we can see that the ﬁrst

term on the right hand side of (8.9) dominates, unless DE

..DE

. The response (to

the lack of highly accurate ab initio calculations) has often been to make correlations

which are expected to be true if the basic model is on the right track. If metal–semi-

conductor and semiconductor–semiconductor band alignments are similar in origin,

then (E

) for the metal should parallel (E

) for the semiconductor, and this

equals the (negative of the) barrier height for a p-type metal-semiconductor contact

, since the relevant acceptor states are close to E

. This correlation, shown in ﬁgure

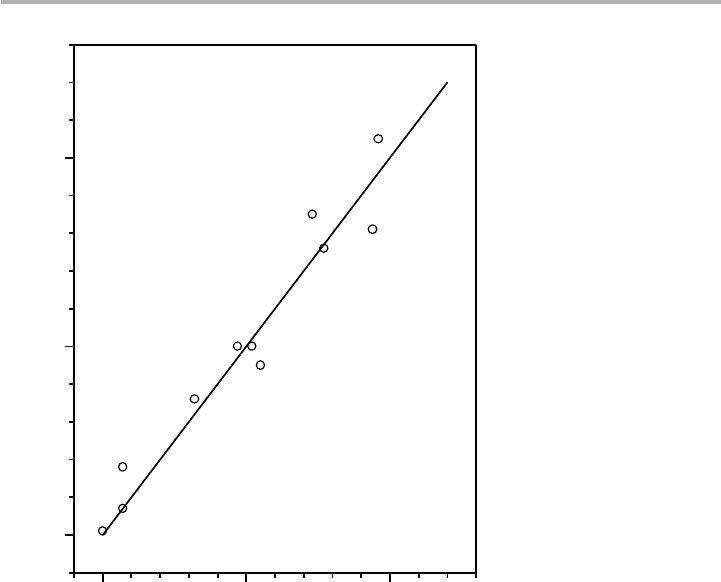
8.12, is perhaps the most successful prediction of the MIGS model.

The challenge for quantum mechanical calculations is that barrier heights and band

oﬀsets are of order 0.3–1.0 eV, and can be measured to 6 0.02 eV precision. As can be

seen in ﬁgure 8.12 and in table 8.1, predictions in the late 1980s were good to

⬃ 60.1–0.15 eV. Some calculations have improved to a secure 6 0.1 eV, but claims to

be much better are suspect. In particular, it is not easy to ensure that charge neutrality

8.2 Semiconductor heterojunctions and devices 273

Figure 8.11. Band lineups at semiconductor–semiconductor interfaces, which result in (a) a

strong interface dipole, (b) almost no interface dipole (after Tersoﬀ 1987, redrawn with

permission).

+ + +

- - -

(a)

+ + +

- - -

(b)

is maintained across the interface to the required accuracy. One important model of

semiconductor interfaces which builds in this requirement is the ‘model solid’ approach

originated by Van de Walle & Martin (1986, 1987), further developed by Van de Walle

(1989), and reviewed by Franciosi & Van de Walle (1996) and Peressi et al. (1998) as

discussed in the next section.

8.2.3 Opto-electronic devices and ‘band-gap engineering’

Several books (e.g. Butcher et al. 1994, Kelly 1995, Davies 1998) and many conference

articles make it clear that artiﬁcially tailored semiconducting heterostructures now

form the leading edge of device technology, and indeed have done so for the past 20

years. By alternating thin layers of, for example, GaAs with (AlGa)As, one can produce

structures with remarkable opto-electronic properties, such as the multiple quantum

well (MQW) laser, and many others. They are fabricated by techniques such as MBE

or MOCVD (see section 2.5) and can be patterned using optical or electron-based

lithography techniques to form real devices (see e.g Kelly 1995, chapters 2 and 3).

274 8 Surface processes in thin ﬁlm devices

Figure 8.12. Correlation of the p-type Schottky barrier height for Au contacts

with the

calculated position of the charge neutrality level (E

) for several 3–5 and 2–6

semiconductors (after Tersoﬀ 1987, replotted with permission).

0.0 0.5 1.0

0.0

0.5

1.0

Neutrality level

(eV)

Schottky height,

(eV)

These devices come in various geometries. Many devices use a material structured in

one dimension, perpendicular to the layers, so that the electrons are conﬁned in this

direction and move (freely) in the other direction; this is the basis of the 2D-electron

gas (2DEG) which is used for studying the quantum Hall eﬀect (QHE) and many other

eﬀects. As can be seen in the n-type case illustrated in ﬁgure 8.13, the 2DEG exists in

a thin layer where the conduction band of the narrower gap material dips below E

;

there are equivalent cases for p-type material. There are also 1D wires (1DEG) and

zero-D dots (0DEG).

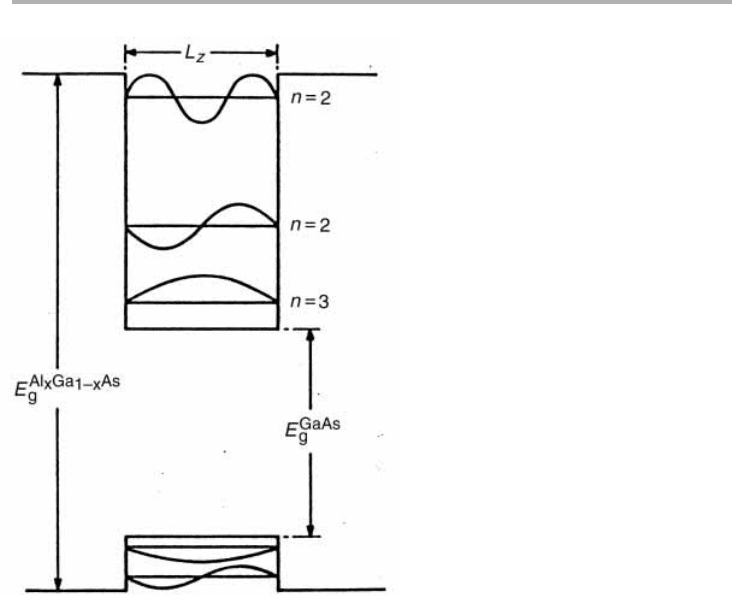
In a QW heterostructure, the electrons and holes are conﬁned in a thin ﬁlm of the

narrower band gap material, e.g. GaAs, with E

51.42 eV at room temperature or

1.52 eV at 0 K, surrounded by an alloy of (AlGa)As, as illustrated in ﬁgure 8.14 (the

band gap of AlAs is 2.15 eV at room temperature, see table 8.1). A key quantity is the

valence band oﬀset, DE

, or the conduction band oﬀset DE

, i.e. (DE

2DE

). The

energy levels in the well are determined by how the band gap diﬀerence DE

is parti-

tioned between DE

and DE

. The quantity Q

5DE

/DE

, the proportion of the gap

diﬀerence which appears in the conduction band, is often quoted in data tables, but

DFT and other theoretical models typically give DE

with best accuracy.

Although the quantization of the energy levels in the z-direction leads to the 2DEG,

electrons and holes can move in the x and y directions parallel to the interface; so what

is shown in diagrams such as ﬁgures 8.13(a) or 8.14 is not a unique level, but the onset

energy of a subband. Within a subband, the 2D density of states is a step function as

shown in ﬁgure 8.13(b). For GaAs and similar materials, there are also light and heavy

holes, related to spin-orbit splitting in the valence band, and the material, in contrast

to Si, has a direct band gap. Thus the optical properties of the well are now determined

by the electron and hole masses (three parameters), the well width L

,andQ

. Duggan

(1987) has given a useful introduction to the determination of optical properties, typ-

ically pursued via optical absorption or photoluminescence (PL) experiments;

another useful starting point is Kelly (1995, chapter 10). As shown in ﬁgure 8.15, the

optical absorption (transmission) spectrum shows peaks which can be identiﬁed with

light and heavy hole transitions. Note, in passing, that PL experiments only work at

low temperatures, as the transitions are too broad at room temperature, and the

8.2 Semiconductor heterojunctions and devices 275

Figure 8.13. A semiconductor heterostructure giving rise to a 2D-electron gas at zero bias in

n-type material. The energy levels shown in (a) are the onset energies of subbands whose

density of states, N(E), is indicated in (b).

(a)

(b)

∆E

()z

1st

subband

1st subband

2nd

3rd

2DEG

NE()

3D Envelope ~E

1/2

number of parameters involved causes quite a bit of diﬃculty for data analysis.

Nevertheless, several parameters can be determined (or assumed in order to get better

values of other parameters), the early work leading to Q

values typically in the range

0.6–0.8 for GaAs/AlGaAs heterostructures, and subsequently reﬁned towards the

lower end of this range (Yu et al. 1992, Davies 1998).

In the same volume (Capasso and Margaritondo 1987) there are extensive tabula-

tions of early experimental valence band oﬀsets DE

, obtained largely by photoemis-

sion, but also by other techniques including extensions of C–V proﬁling and DLTS.

Raman scattering has also found a useful niche (Menéndez et al. 1986, Menéndez &

Pinczuk 1988) to measure inter-subband transitions for electrons, and hence DE

Later compilations and comments are given by Yu et al. (1992), Butcher et al. (1994)

and Franciosi & Van de Walle (1996). Technology moved ahead in the 1990s, e.g. via

the infrared devices based on resonant tunneling via minibands (Capasso & Cho 1994),

but the science had more or less stabilized by the late 1980s. Table 8.1 gives some rep-

resentative DE

values for low strain interfaces.

However, it has become clear that pictures such as ﬁgures 8.10 and 8.11 are only a

ﬁrst step, and that too simple pictures may give a misleading impression. Valence band

276 8 Surface processes in thin ﬁlm devices

Figure 8.14. Simple energy levels in a quantum well, consisting of a narrower band gap

material (GaAs) surrounded by a higher band gap material (Al

12x

As). Note, however, that

the well wavefunctions must in practice spread into the surrounding layers, and the real band

structure modiﬁes this picture (from Duggan 1987, reproduced with permission).