Venables J. Introduction to Surface and Thin Film Processes

Подождите немного. Документ загружается.

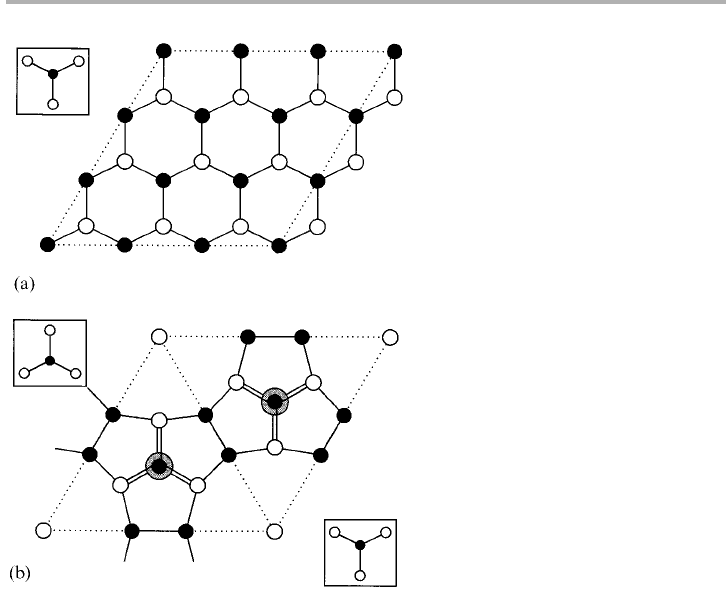
and the ring at the corners at the intersection of cell edges. Without the stacking fault,

we simply have the adatoms, which are arranged in a 232 array. The Ge(111) structure

is thought to be based simply on these adatoms; within the cell there are two local

geometries, subunits of 232 and c234; together they make the larger c238 recon-

struction as determined by X-ray diﬀraction (Feidenhans’l et al. 1988); reviews of this

technique plus many structural details are given by Feidenhans’l (1989) and Robinson

& Tweet (1992). In case you think it is always easy for great scientists, it isn’t; for

example, Takayanagi & Tanashiro (1986) generalized their Si(111) 737 model to

produce a model of Ge(111)c238 based on dimer chains – too bad, wrong choice!

The high temperature 131 structure is often written ‘131’, meaning ‘we know it

isn’t really’; both Si and Ge are thought to form a disordered structure of mobile

adatoms which may locally be in 232 or similar conﬁgurations. Diﬀuse scattering from

these adatoms has been seen for both Si and Ge(111), e.g. using RHEED (Kohmoto &

Ichimiya 1989) and medium energy ion scattering (MEIS) (Denier van der Gon et al.

1991). Similar structures are expected on Ge/Si mixtures, where Ge segregates to the

7.2 Case studies of reconstructed semiconductor surfaces 237

Figure 7.5. Simple Si(111) surface structures (a) bulk terminated, showing a 333 cell for

comparison with (b) 333 DAS structure. In (a) the open and full circles show unrelaxed atoms

of the ﬁrst layer (three-fold) and second layer (four-fold) coordinated. In (b) the second layer

atoms form the dimers along the (dotted) cell edges, which is coupled to the existence of the

stacking fault in the lower left hand half of the cell (small boxes). The larger shaded circles are

the adatoms, which are three-fold coordinated, each replacing three dangling bonds by one

(after Chadi 1989, redrawn with permission).

surface because the lower binding energy. These details are also fascinating and are dis-

cussed in section 7.3.3.

Are there any further checks on these models, and can we make sense of them? STM

has been invaluable; adatoms were seen in the original pictures by Binnig et al. (1982),

and subsequent work by many people showed up back bonds and other features of the

electronic structure; i.e. one gets diﬀerent pictures as a function of bias voltage, because

diﬀerent states are active. The most ambitious, yet relatively simple, attempt to under-

stand the various structures is that by Vanderbilt (1987), where he tries to estimate the

energy costs of the stacking fault (f) and of the corner holes (c), expressed as a ratio to

the dimer (domain wall) energy. He then draws a phase diagram, shown in ﬁgure 7.7.

This exhibits a series of DAS structures if f is small, which have increasing (2n11) peri-

odicity as c increases. At larger values of f, the stacking fault is unfavorable, and there

is a transition to an ordered adatom structure, notionally the c238.

This simple diagram explains how Si and Ge could be close together on such a

diagram, and yet have such diﬀerent structures. It also explains (in the same sense) how

the surface stress, quenching, or Ge addition to the surface can give rise to 535, 939,

and mixed surfaces. Beautiful STM pictures illustrating all these possibilities have been

published by Yang & Williams (1994); one example is shown here in ﬁgure 7.8. The

important point to note is that these diﬀerent reconstructions do not have the same

areal density of atoms; so the change from one structure to another requires a lot of

238 7 Semiconductor surfaces and interfaces

Figure 7.6. The equilibrium 737 DAS structure. All the DAS features are present, with 12

adatoms plus seven ‘rest atoms’, three in each half of the cell plus one in the middle of the

corner hole. There are thus 19 dangling bonds left out of 49 for the unreconstructed structure.

This reduction in energy is obtained at the cost of substantial internal strain energy, stretching

over at least four layers (after Takayanagi et al. 1985, redrawn with permission, and later

authors).

Adatoms

Second layer

and 'rest' atoms

Third layer

including dimers

Fourth layer

adatom movement, and can nucleate 2D islands or pits; the microstructure thus

becomes very complex, depending on the kinetics in detail.

7.2.4 Si, Ge and GaAs(001), steps and growth

The geometry of the basic 231 reconstruction of Si(001) was fully described in section

1.4. We need to recall the formation of the dimers, their organization into dimer rows

(perpendicular to the dimers), and the correlation with surface steps (Chadi 1979,

1989, Griﬃth & Kochanski 1990). There has been much debate as to whether the 23

1 reconstruction is symmetric, or asymmetric; by now you will realize that this is the

same question as whether the surface is metallic or semiconducting. A consensus has

emerged that the Si dimer is asymmetric, but that the energies are so close that the

dimer ﬂips between two equivalent states – either the left-hand or the right-hand atom

is up at any one time. At high temperature, this is like having a low frequency anhar-

monic vibrational mode; at low temperature, ordered arrays of up and down dimers

can give various superstructures, such as p232 or c234.

There are a host of such calculations in the literature: one (Ramstad et al. 1995) gives

the c432 as the lowest energy structure, and calculates by how much it is stable. The

dimerization gives a large energy gain over the unreconstructed 131 structure, about

2 eV per dimer. The asymmetric dimer is favored by a further 0.2 eV; ordering these

dimers into either the p232 or c432 gains a further 0.02 eV, and the eventual stabil-

ity of the c432 is a mere 0.002 eV/dimer. It is not entirely clear whether we should

believe this slender margin, but it is clear why the complex superstructures will not be

stable at high temperatures. Finite temperature molecular dynamics simulations have

mapped out the timescale on which the dimers ﬂip between the two positions; an

example which takes account of the actual p232 or c432 structure is shown in ﬁgure

7.9 (Shkrebtii et al. 1995). Here it can be seen that dimers ﬂip, and also twist, causing

7.2 Case studies of reconstructed semiconductor surfaces 239

Table 7.2. Calculated energies of reconstructed Si and Ge(111) surfaces

(eV/1

1 cell)

131231232333535737

Material relaxed cleaved adatom DAS DAS DAS

Si(111) ⬃1.39

1.239

⬃1.12

1.196

1.168

1.153

, 1.179

Ge(111) ⬃1.15

⬃1.04

0.88

⬃1.34 ,1.40

⬃1.08 ,1.20

References: (a) Payne (1987), Payne et al. (1989); (b) Meade & Vanderbilt (1989). The Ge

calculations were not well converged, and should be lower than the Si values; the ⬃values

assume that the changes on convergence are the same as for Si; (c) Stich et al. (1992); (d)

Brommer et al. (1992). The only experimental values available date from 1960 and are

1.24 J·m

for cleaved Si(111) (0.998 eV/131 cell) and 1.10 J·m

for Ge(111) (0.952 eV/131

cell) (Kern et al. 1979); these values are not unreasonable, but they have unknown error bars.

240 7 Semiconductor surfaces and interfaces

Figure 7.7. Model phase diagram of surface structures for the Si(111) surface; c and f are

measures of the eﬀective corner hole and stacking fault energies relative to the dimer (domain

wall) energies. The arrows show possible trajectories that can occur by increasing the adatom

density, and hence the chemical potential of Si which acts to compress the surface phase (after

Vanderbilt 1987, and Yang & Williams 1994, reproduced with permisison).

Figure 7.8. Coexistence of reconstructions on Si(111) (a) area approximately 1003 100 nm

showing 737, 939 and regions with higher densities of adatoms; (b) atomically resolved

image of a high adatom density area 43343 nm

showing 737, 939 and other

reconstructions where adatoms are seen individually (after Yang & Williams 1994).

(a)

(b)

7.2 Case studies of reconstructed semiconductor surfaces 241

Figure 7.9. Dimer buckling (z-motion) and twisting (y-motion) on Si(001) revealed in a ﬁnite

temperature molecular dynamics simulation at 900 K, showing two of the four dimers in a

(432) cell (after Shkrebtii et al. 1995, reproduced with permission).

changes of structure, roughly every 0.5–1 ps. The amplitudes are suprisingly large,

namely .0.05 nm up and down (buckling) and sideways (twist plus shift) ⬃0.03 nm at

900 K. These amplitudes correspond to tilt angles in the range 16–19°, though this

value does vary somewhat between the diﬀerent calculations (Krüger & Pollmann

1994, 1995, Ramstad et al. 1995, Srivastava 1997).

For Ge (001), and more recently Ge/Si (001) also, there has been great interest in

whether these surfaces are also asymmetric, in what way, and in establishing the trends

in bond angles (Tang & Freeman 1994). All these reconstructions reduce the symme-

try of the surface, which results in diﬀusion and growth properties that are very aniso-

tropic, and alternate across single height steps. The growth of devices based on

Ge/Si(001), or GaAs on Si or Ge(001) gives rise to many fascinating problems. There

is a vast literature on these topics, and even more unpublished empirical knowledge in

the ﬁrms who make devices based on such materials. Some of these issues are aired in

section 7.3; but the last word on these subjects is a long way in the future.

7.3 Stresses and strains in semiconductor ﬁlm growth

7.3.1 Thermodynamic and elasticity studies of surfaces

In the previous section we referred to the eﬀects of stress on surface reconstructions.

Before proceeding further it is time to return to section 1.1.3, where it was noted that

surface stress had the same units as surface energy, but that the stress

, sometimes

written f

, is a second rank tensor, whereas the surface energy

is a scalar quantity.

This complication is the main reason for delaying consideration of surface stress until

now. Somehow, the stress has potential to do work, but doesn’t actually do so unless

there is a surface strain

associated with it. In that case the stored internal energy,

assuming linear elasticity, is given as in bulk material by

DU5

⁄2兺

, (7.3)

where the summation is assumed to be over repeated suﬃces, and in the case of a

surface i, j51 or 2. The creation of a new surface, area A, in a strained solid proceeds

in two stages in either order: we can strain the solid ﬁrst and then create the surface, or

vice versa. The work done, dW analogous to (1.3) is then

dW5d(

A)5

dA1Ad

. (7.4)

Noting that dW5A兺

we can then deduce the relation for the individual compo-

nents of the stress tensor

g

«

, (7.5)

since dA5A

, where

is the Kronecker delta (i.e. 1 for i5j and zero otherwise).

If the surface has three-fold rotation symmetry or higher, then the oﬀ-diagonal terms

of (7.5) are zero and the diagonal terms are equal, so the surface stress

is isotropic in

the surface plane.

242 7 Semiconductor surfaces and interfaces

The thermodynamic background leading to (7.5) is given by Cammarata (1994),

who acknowledges that there has historically been much confusion on this topic. In

addition, his paper describes calculations on the values of surface and interface stresses

in particular materials. For example, noble metals are under positive surface stress if

they have unreconstructed surfaces, because the surface atoms want to immerse them-

selves in a higher electron density to compensate for the loss of neighbors caused by

the surface. The stress of the unreconstructed surfaces is calculated to be much larger

for Au than for Ag; this is consistent, qualitatively at least, with the fact that Au(111)

has the contracted 2331 herringbone structure, and Au(001) the more close-packed

5320 structures described in section 6.1.2, whereas Ag(111) and (001) are both unre-

constructed (Needs et al. 1991). For semiconductors such as Si and Ge(111), the diﬀer-

ent reconstructions are calculated to have diﬀerent surfaces stresses as well as energies,

and indeed it is thought that the stability of the 737 reconstruction results from partial

compensation of positive and negative stresses between diﬀerent layers (Meade &

Vanderbilt 1989). However, the point to remember is that the stability of these surfaces

depends on the surface energy, not the stress; the existence of the stress is only a reason

why the surface might want to adopt a diﬀerent structure.

This situation changes if we apply a stress to the surface by external means; now

work can be done by and on the surface, and the conﬁguration of the surface may

change in response to the applied stress. The 231 reconstruction on Si(001), discussed

in detail in section 1.4.4, is only mirror (2mm) symmetric, and so the surface stress

tensor is not isotropic. Since single-height steps are associated with a switch in domain

orientation, there is a change in surface stress across each step, and this can be por-

trayed as a force monopole F

at each step, alternating in sign between S

and S

steps

and numerically equal to the diﬀerence in stress tensor components (

⬜

Calculations for Si(001) indicate that the value of

is positive parallel to the dimer

bond direction, and

⬜

is negative in the direction perpendicular to it, thus parallel to

the dimer rows. If the steps can move, F

couples to the external strain, work is done,

and the equilibrium domain conﬁguration of the surface changes.

The classic experiment was the observation of changes in domain population on the

Si(001) surface at elevated temperature (⬃625 K) in response to bending a Si wafer,

studied by LEED and STM by Webb and co-workers (Webb 1994) illustrated in ﬁgure

7.10. With a surface strain of only 0.1%, the domain population as observed by LEED

half-order intensities was shifted from equal areas to more than a 90–10 distribution

(Men et al. 1988); follow-up studies by STM showed not only this distribution of areas,

but also the statistics of kinks along ledges (Swartzentruber et al. 1989, Webb et al.

1991). A model developed by Alerhand et al. (1990) was the among the ﬁrst to describe

the elastic and entropic interactions between the steps, and to ﬁt such experiments so

that energies for the direct step–step interactions, and for kink energies on S

and S

steps could be extracted. We should note in passing that the original straining experi-

ments were unsuccessful, since the steps cannot move at room temperature because of

insuﬃcient surface mobility. It is necessary that kinks can move, and that adatoms

and/or ad-dimers can diﬀuse along and detach from steps for local equilibrium to be

established.

7.3 Stresses and strains in semiconductor ﬁlm growth 243

A very interesting development consisted of depositing sub-ML amounts of Ge on

the Si(001) surface and repeating the same series of straining experiments (Wu &

Lagally 1995). By this means it was shown that the surface stress anisotropy could be

made to change sign as a function of Ge concentration, passing through zero at around

50.8. The anisotropy was measured for pure Si as F

51.0 6 0.3 eV/

, where

the area per 131 surface unit cell. For 2ML Ge/Si (001) F

had decreased to 20.9 6

0.3 eV/

. Comparison with calculations, including those by García & Northrup

(1993), indicated that the main change is the strong decrease in

with increasing Ge

coverage, with

⬜

staying essentially constant. There is clearly scope for studies on

other surfaces with low symmetry such as (113), which is a possible substrate for

quantum wires and grooves (Knall & Pethica 1992, Baski et al. 1997).

All these experiments should be seen in the context of the limited amount of data

which exist on the equilibrium form of Si and Ge crystals. These have either been

obtained on crystals of a few micrometers in size at relatively high temperatures

⬃1050°C, which parallel the data on metals explored in sections 1.2.3 and 6.1.4

(Bermond et al. 1995, Suzuki et al. 1995), or via the formation of ⬃10 nm size helium-

ﬁlled voids after ion implantation by annealing to temperatures between 600–800°C

(Follstaedt 1993, Eaglesham et al. 1993). For silicon, the latter authors agree that

111

is the minimum in the free energy, and estimate

001

111

51.09 6 0.07, and

110

111

244 7 Semiconductor surfaces and interfaces

Figure 7.10. The asymmetry of half-order LEED intensities from 231 and 132 domains on

Si(001) surfaces as a function of surface strain. The domain compressed along the dimer bond

is favored (after Men et al. 1988, replotted with permission).

1.07 6 0.03 (Follstaedt 1993); Eaglesham et al. (1993) give

001

111

in the range 1.11 6

0.03,

113

111

⬃1.12 and

110

111

⬃1.16 at ⬃800 °C.

However, at the higher temperature of 1050 °C (1323 K, which is above the 737to131

transition), Bermond et al. (1995) ﬁnd a smaller anisotropy (⬃4%), as one might expect,

but they also ﬁnd that the ordering has changed to

111

110

113

001

. A curious

feature is that the (001) face does not have a true cusp in the equilibrium form, which con-

sists largely of {111} and {113} facets and rounded regions. This is probably due to the

long range stress ﬁeld, and the associated strain energy, due to the (231) surface domains,

which results in the spontaneous formation of steps discussed by Alerhand et al. (1990)

and observed by using LEEM by Tromp & Reuter (1992, 1993). A reminder that impur-

ities can be inﬂuential in such measurements was shown by the (reversible) segregation of

0.3% carbon to create extra facets, which are not in the clean equilibrium form.

Many studies on facetting transitions on Si and Ge surfaces vicinal to (111), includ-

ing the eﬀect of the 737 to 131 transition for Si, have been made using LEED, LEEM

and STM by Bartelt, Williams and co-workers, as reviewed by Williams et al. (1993),

Williams (1994) and Jeong & Williams (1999). All this work suggests that at the higher

temperatures the free energy diﬀerences between the various faces {hkl} are quite

small, due to a subtle balance of substantial energetic and entropic factors. Large

amplitude motion of steps on Si(111) has been observed also by REM (Pimpinelli et

al. 1993, Suzuki et al. 1995), the analysis of which also implies a sizable adatom pop-

ulation on the terraces to mediate the step movement.

The surface entropies involved in these transitions are unknown, but microscopy is

beginning to visualize directly some conﬁgurations (and motion) involved on the time-

scale of 1 s and upwards. Molecular dynamics studies, as illustrated here by ﬁgure 7.9,

can be used to estimate the entropy associated with conﬁguration and motion on the

pico-second time scale. Another point to note is that the latent heats of melting of Si

and Ge are almost a factor of 2 higher than that of close-packed metals which melt at

similar temperatures. The interrelation of these apparently isolated facts can be

explored further via project 7.4; a link is the angular nature of sp

bonding in semicon-

ductors, and its (partial) disappearance in the liquid state.

7.3.2 Growth on Si(001)

The classic substrate for semiconductor growth is Si(001), since this has the simplest

structure, and is used for growth of most practical devices. Typically device growers use

a surface which is tilted oﬀ-axis by about 2–4°, to form a vicinal surface which contains

a regular step array. The reason for this is to promote layer by layer growth, sometimes

referred to as step-ﬂow, and to suppress random nucleation on terraces; nucleation is

typically not wanted, because it increases the possibility of incorporating defects (e.g.

threading dislocations) which have bad electrical properties. Thus the fact that higher

miscut angles favor double-height steps (Chadi 1987, Tong & Bennett 1991, de Miguel

et al. 1991, Men 1994) is of major importance for growing compound semiconductors

such as GaAs (on Si), since single steps produce anti-phase boundaries, across which

Ga and As are misplaced.

7.3 Stresses and strains in semiconductor ﬁlm growth 245

Moreover, materials grown on such a substrate typically have a sizable misﬁt, which

may be accommodated initially by strain, but eventually by missing dimer rows at the

atomic level, or by dislocations. Most growers search for low misﬁt systems, so that dis-

location introduction is delayed beyond the so-called critical thickness (Matthews

1975, Matthews & Blakeslee 1974, 1975, 1976, People & Bean, 1985, 1986). The

bonding changes during semiconductor growth are extremely complex, since any

surface reconstruction has to be undone in order for growth to proceed; at low temper-

atures there is the possibility of creation of many, largely unwanted, metastable struc-

tures. On the other hand if growth of complex multilayer structures, such as multiple

quantum wells (MQWs) with diﬀerent compositions, is conducted at too high temper-

atures then they will be degraded by surface segregation and interdiﬀusion. Device

engineers are always treading a ﬁne line in trying to grow crystals at the lowest practi-

cable temperature – reducing the ‘thermal budget’; many of the more technical

methods described in section 2.5 have been introduced solely for this reason.

There have been many studies of Si/Si(001) growth primarily using STM, in addi-

tion to spot proﬁle analysis using LEED (Heun et al. 1991, Falta & Henzler 1992) and

RHEED (Tong & Bennett 1991). Large area STM pictures such as ﬁgure 7.11 are very

helpful (Mo & Lagally 1991, Liu & Lagally 1997); one can identify both S

and S

single height steps which have very diﬀerent roughness due to diﬀerent edge energies

and the anisotropy of diﬀusion.

In one detailed study, the nucleation density N of 2D islands on the terraces was

observed as a function of R and T, and an analysis similar to that of section 5.2 per-

formed, but taking into account the diﬀusion anisotropy, and the anisotropy in binding

246 7 Semiconductor surfaces and interfaces

Figure 7.11. STM images of Si/Si(100) showing diﬀusional anisotropy of adatoms, and the

eﬀects of S

and S

steps, after 0.1 ML deposition at R50.15 ML/min, T5(a) 563 K,

(b) 593 K. The surface steps down from upper left to lower right. In (a) anisotropic islands can

be seen on all terraces; the underlying dimer rows are orthogonal to these islands. In

(b) diﬀusion is more rapid, so denuded zones are observed only on (231) terraces (after Mo &

Lagally 1991, reproduced with permission).

(a)

(b)