Venables J. Introduction to Surface and Thin Film Processes

Подождите немного. Документ загружается.

ations with this characteristic decay time

are caused by adatom diﬀusion in or out of

the probe hole, and

⬃r

/4D. So measuring the decay time yields the diﬀusion

coeﬃcient. The subtlety can be increased further: using a slot in diﬀerent orientations

allows one to explore diﬀusion anisotropy, since the measurement is dominated by

diﬀusion parallel to the short axis of the slot of half-width x;now

⬃x

/2D.An

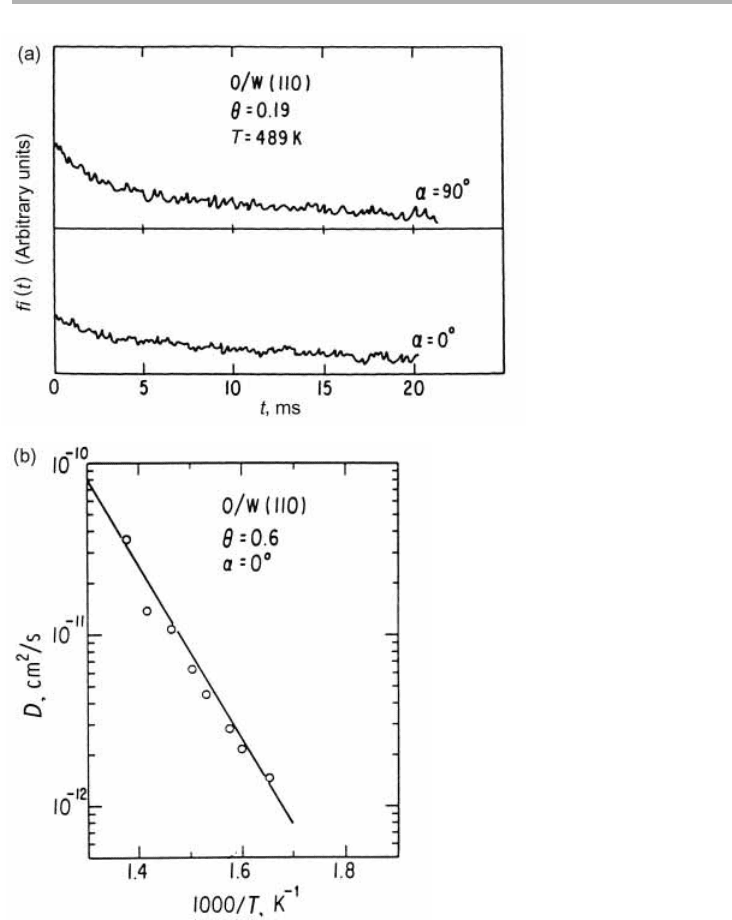
example of O/W(110) is shown in ﬁgure 6.15; in this case the work function of the

oxygen covered surface is greater than the clean metal, so the adsorbate reduces emis-

sion. Note that O-diﬀusion was found to be anisotropic in the ratio about 2:1, faster

parallel to [1

10] (Tringides & Gomer, 1985).

Adsorption is useful for an electron source if the adsorbate increases emission. The

stringent vacuum requirements of ﬁeld emission can be reduced somewhat if one both

increases the operating temperature, and also uses an adsorbed layer which reduces the

work function. This is thermal ﬁeld emission (TFE). Typical thin layers, which have

long been used in TV and other sealed tube applications, are refractory (Ba, Sr) oxides,

pasted onto, or indirectly heated by, the W ﬁlament; however, these coatings degrade

badly if let up to atmosphere.

For high performance SEM applications, W(001) tips coated with Zr/O have been

used as TFE sources; this cathode has

⬃2.6–2.8 V (Orloﬀ 1984, Swanson 1984).

When operated at T⬃1800 K, the molecules adsorbed from the vacuum, or diﬀused

from the support, do not remain on the surface long enough to cause the current to

decay with time; the tips can also have a larger radius than for CFE at a given anode

voltage V

, due to the lower

. In higher current applications, it is the angular current

density (I/

) which is more important than the brightness: the angular current density

can be in excess of 1 mA/sterad. TFE is a successful compromise for many applica-

tions: a reasonable current which is stable in moderate (,10

mbar) vacuum, an inﬁ-

nite lifetime barring accidents, requiring only routine preparation after bakeout: all of

which is just as well, considering the initial cost!

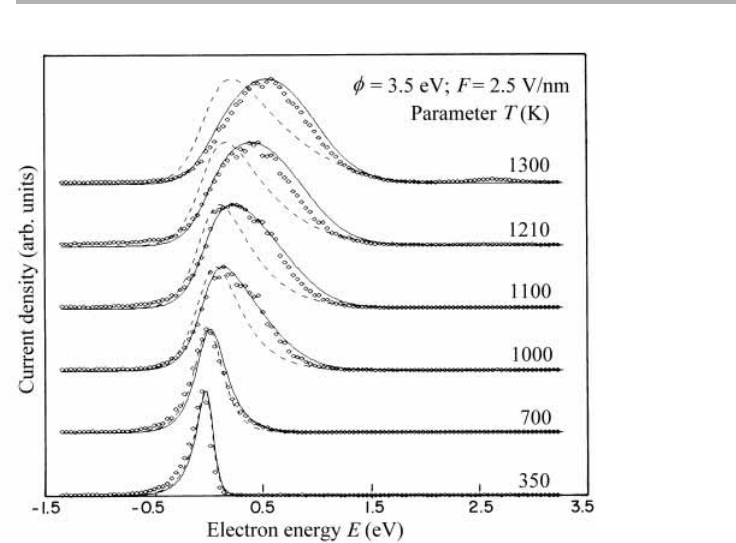
Research into alternative CFE/TFE emitters also continues, and papers occasionally

appear in the journals. An example detailing the TFE properties of LaB

(Mogren &

Reifenburger, 1991) emphasized that the emission process is rather more complex than

the simplest Fowler–Nordheim treatment presented here, and needs to take into

account the actual density of states in the material just above the Fermi level. This

eﬀect is indicated by the diﬀerence between the full and dashed lines in ﬁgure 6.16;

additionally, this paper showed that the current decay after ﬂashing may be due to the

removal of emission from surface states. Note that the narrow energy distribution is a

feature of CFE which gets lost to some extent in TFE. The highest performance ana-

lytical STEM and STEM-spectroscopy instruments use CFE primarily for this last

reason. Once the vacuum in the source region has been improved to ,10

210

mbar, the

advantages of CFE can be realized in such applications.

6.2.4 Secondary electron emission

When a sample is bombarded with charged particles, the strongest region of the elec-

tron energy spectrum is due to secondary electrons. We have discussed this extensively

6.2 Electron emission processes 207

in chapter 3, for example in relation to ﬁgure 3.7 in section 3.3, and to the operation of

the SEM. The secondary electron yield depends on many factors, and is generally

higher for high atomic number targets, and at higher angles of incidence. There is a lot

of information in this secondary electron ‘background’, but, unlike Auger and other

electron spectroscopies, it is not directly chemical or surface speciﬁc in general.

However, there are cases where the secondary electrons can be seen to convey more

208 6 Electronic structure and emission processes

Figure 6.15.(a) Current–current correlation functions for two orientations, diﬀusion

perpendicular and parallel to [1

10]; (b) diﬀusion coeﬃcients for O/W(110) parallel to [1

10]

(from Tringides & Gomer 1985, reproduced with permission).

speciﬁc surface information. Under clean surface conditions, a change of surface

reconstruction, or an adsorbed layer, will change the work function, the surface state

occupation, and may also, in a semiconductor, change the extent of band bending in

the surface region. A technique developed from this eﬀect is biased-secondary electron

imaging (b-SEI), since biasing the sample negatively (anywhere from 210 to ⬃2500

V) causes the low energy electrons to escape the patch ﬁelds at the surface. This signal

is much more sensitive for imaging than the corresponding Auger microscopy, as dis-

cussed in section 3.5. It has been shown that this technique is suﬃcient to detect sub-

ML deposits with good SNR, as illustrated in ﬁgure 3.21 for Ag/W(110). The case of

Cs/W(110), studied earlier by Akhter & Venables (1981), showed that phase transitions

could be observed and the activation energy for Cs surface diﬀusion measured, com-

plementing original values by Taylor & Langmuir in the 1930s. The patch ﬁeld eﬀect is

very strong in this case, extending for distances of more than 0.1 mm away from the

Cs/W boundary at low bias ﬁelds.

Once again, the corresponding spectroscopy is useful in determining the origin of

the contrast (Janssen et al. 1980, Futamoto et al. 1985, Harland et al. 1987). For 2 ML

Ag deposited onto W(110) an increase in the secondary yield at the lowest electron

energies E was observed, which is readily explained by a decrease in the work function.

This form of surface microscopy has been exploited to measure diﬀusion of sub-ML

6.2 Electron emission processes 209

Figure 6.16. Energy distributions during TFE from LaB

as a function of temperature. Full

lines are a calculation for a detailed ﬁeld emission model including the eﬀect of a peak in the

density of states at energies just above E

, compared with the Fowler–Nordheim expression

for

53.5 eV and F52.5 V/nm (Mogren & Reifenburger, 1991, reproduced with permission).

and multilayer deposits over large distances (.10 mm) for both Ag/W(110) (Jones &

Venables 1985) and Ag/Fe(110) (Persaud et al. 1994, Noro et al. 1996), as described in

section 5.5.2. However, in the metal–semiconductor case of sub-ML Ag/Si(111) there

is also a yield increase at higher E, a change in band-bending is involved, as discussed

later in section 8.1. In the case of sub-ML Cs/Si(100), the detection sensitivity of b-SEI

was pushed to below 1% of a ML, reﬂecting the large surface dipole moment caused

by Cs adsorption at low coverage (Milne et al. 1994, 1995).

6.3 Magnetism at surfaces and in thin ﬁlms

In this section, some concepts that are important in magnetism at and near surfaces

are introduced, and examples of techniques sensitive to magnetic eﬀects are given.

Magnetism has a long history, and it is not possible to cover this adequately in one

section of one chapter. If you are going to study thin ﬁlm magnetism in detail, you will

also need access to a modern textbook (e.g. Jiles 1991 or Craik 1995), plus review arti-

cles and chapters (e.g. Heinrich & Cochran 1993, Heinrich & Bland 1994). Here we ﬁrst

consider aspects of symmetry and symmetry breaking in relation to phase transitions,

and then introduce some surface techniques which are sensitive to magnetic eﬀects.

Finally, we discuss some aspects which may become important in the next generation

of thin ﬁlm devices based on magnetism.

6.3.1 Symmetry, symmetry breaking and phase transitions

Arguments about symmetry, and symmetry breaking, ﬁgure strongly in the magnetic

literature. Magnetism is often the prototype system in discussions of phase transitions.

The Weiss theory of ferromagnetism published in 1908 (Ashcroft & Mermin, chapter

33, or Kittel, chapter 15) for example, is one of the earliest examples of a mean ﬁeld

theory applied to a (second order) phase transition. Onsager’s exact solution of the 2D

Ising model in 1944 was couched in terms of a magnetic transition. In the book series

edited by Domb, Phase Transitions and Critical Phenomena, many of the articles and

theorems stem from magnetic interests. There is a discussion of Onsager’s papers in

volume 1 of this series by Temperly (1972).

One such theorem is that due to Mermin & Wagner, which shows that magnetic long

range order (in the absence of anisotropy) is impossible for a Heisenberg spin system

in 2D or 1D, whereas it is clearly possible in 3D systems. The argument goes as follows.

In an ordered lattice of magnetic spins which can have any orientation, such as exists

in a ferro- or antiferro-magnet, the excitations are spin waves at low temperature. In

these waves, the spins on neighboring lattice sites twist with respect to each other,

giving rise to a magnetic energy

(k) proportional to k

; these quantized excitations are

called magnons. Then we count the number of magnons, using Bose–Einstein statis-

tics and obtain

兰

g(k) 冓n(k)冔dk, (6.10)

210 6 Electronic structure and emission processes

integrating from zero to inﬁnity, with the density of states g(k)5dn/dk5k/2p appro-

priate for

5Ak

. The number of magnons, n

, then is given by substituting for 冓n(k)冔,

and in the high temperature limit, this gives

兰

(k k

T/hAk

)dk⬃

兰

dk/k⬃[ln (k)], (6.11)

which diverges at the lower limit.

This means that theoretically we cannot have long

range order in 2D, because long wavelength (low k) excitations are possible in these

systems with negligible energy. The same Mermin–Wagner theorem applies to posi-

tional order in 2D, due to the divergence, also logarithmic, of long range positional

correlations; thus the corresponding theorem has also been invoked in theoretical

studies of adsorption, as discussed in chapter 4.

This theorem has been shown to be of interest in some situations, but usually the

length scales are too long to be of practical interest, and what happens ﬁrst has to do

with symmetry breaking. For instance, you can’t make a free standing monolayer, or a

truly 2D magnetic system. Once we have a monolayer or a magnetic system on a sub-

strate, we have broken the symmetry. Logarithmic divergences are very easy to break;

examples are the ﬁnite energies in the core of dislocations due to atomic structure, or

the inductance of a ﬁnite, versus an inﬁnitesimal diameter, wire. The breakdown of the

Mermin–Wagner theorem for such practical reasons is another case.

6.3.2 Anisotropic interactions in 3D and ‘2D’ magnets

In 3D magnetic systems we have many examples of symmetry breaking. The basic mag-

netic interaction is the exchange interaction related to the spins on a lattice as

E52兺JS

·S

, (6.12)

where the summation is typically limited to neighboring sites only; this is referred to as

the Heisenberg Hamiltonian between spins S

and S

with exchange coupling constant

J. In the presence of an external magnetic ﬁeld H, a unique axis is imposed (orienta-

tional symmetry breaking), because E

52兺m

·H. The combination of these two

terms for S

561/2 is the Ising model which Onsager solved exactly to ﬁnd the magnet-

ization M as a function of T. The approach to the Curie temperature, above which the

system is paramagnetic, goes like

M⬃(T2 T

)

1/8

, (6.13)

rather than the mean ﬁeld exponent of 1/2. These critical exponents are characteristic

of the models as T

is approached, and the dimensionality (two, three or higher dimen-

sions), but are not dependent on the details of the interactions. This is the basis of

interest in universality classes, within which the critical exponents are the same: impress

your friends with ‘… as in the 2D XY model, we can see that …’! An introduction to

these critical exponents is given by Stanley (1971), and the details for 2D systems are

6.3 Magnetism at surfaces and in thin ﬁlms 211

Note that we use k

for Boltzmann’s constant in this section and the next, to distinguish it from the wave-

number k.

described by Schick (1981), Roelofs (1996) and others, as discussed in section 4.5.1.

Magnetism has many other symmetry breaking interactions, and we can’t realisti-

cally discuss them all here. But one very important case is the magneto-crystalline

anisotropy (MCA) energy E

, which is due to the anisotropic charge distribution in the

crystal ﬁeld, and orients the magnetic moments along speciﬁc crystalline axes. The

form of this energy depends on the crystal symmetry, the most often encountered being

uniaxial anisotropy, which, for example, makes the c-axis in h.c.p. cobalt the easy axis

of magnetization; the leading term has the form Ksin

. In a cubic crystal, such as b.c.c.

Fe, we have cubic anisotropy, which is expressed in terms of the direction cosines

to the three cube axes as

(

)1K

1. . . (6.14)

We can see that there won’t be a second order term because

51. The easy

axis for Fe is along the 冓100冔 directions, and this corresponds to K

.0 and K

.2K

/9;

for Ni the easy axis is 冓111冔 (Craik 1995, section 1.11). A practical example is the use of

Fe–4% Si for transformer cores. Why? Not because Si does anything wonderful for the

magnetization of Fe, but because it gives polycrystalline Fe a {100} texture, making it

easy to magnetize in the plane of transformer laminations, leading to small energy

losses when used with alternating currents.

There are several other anisotropic terms, which can be important in particular

circumstances. A very important term is the demagnetizing energy, which is a macro-

scopic eﬀect caused by the shape of the sample, and derives from the magnetic self

energy, E

. This self energy can be expressed as either the interaction of the demag-

netization ﬁeld inside the sample with the magnetization, or equivalently, the integral

of the energy density of the stray ﬁeld over all space. If, for example, the magnetiza-

tion is perpendicular to a thin ﬁlm, there is a large energy due to the dipolar ﬁeld

outside the ﬁlm; but if the magnetization is in the plane of the ﬁlm, this eﬀect is mini-

mized. In real ﬁlms, this causes the formation of domains. These domains can be seen

in transmission, even in quite small samples (not necessarily single crystals), by

Lorentz microscopy (coherent Fresnel, Foucault, and diﬀerential phase contrast

imaging), as described in several papers from Chapman’s group in Glasgow (e.g.

Chapman et al. 1994, McVitie et al. 1995, Johnston et al. 1996, Chapman & Kirk

1997). They can also be seen using electron holography as developed initially by the

Möllenstedt school in Germany and Tonomura’s group in Japan, and further devel-

oped and reviewed by Mankos et al. (1996). In uniaxial crystals such as h.c.p. cobalt,

there will still be a small ﬁeld outside the ﬁlm, connecting two oppositely oriented

domains. In cubic crystals, even this can be avoided, by the formation of small closure

domains at the ends of the ﬁlm. The price paid for these domains is the energy of the

interfaces between oppositely magnetized regions: these are known as Bloch or Néel

walls, depending on the details of how the spins rotate from one domain to the other

(Kittel 1976).

Another term relevant to thin ﬁlms is magnetoelastic anisotropy, or magnetostric-

tion. In this eﬀect, the crystal parameters change because of the magnetism; this

also implies that structure and symmetry changes will inﬂuence the magnetism, as

212 6 Electronic structure and emission processes

exempliﬁed by the much studied system Fe/Cu(001). Fe is b.c.c. in bulk at temperatures

below the b.c.c.–f.c.c. transition at 917°C; the Curie temperature in b.c.c. is at 770 °C,

and f.c.c. Fe is overall non-magnetic, although the calculated details depend very sen-

sitively on the lattice constant. However, when Fe is deposited on a cold (77 K) Cu(001)

substrate, and warmed to room temperature, the magnetization is perpendicular to the

ﬁlm for a coverage ,5 ML, and is parallel for .5 ML. But below 10 ML, Fe is not

b.c.c., but is pseudomorphic with the Cu(001) and is nominally f.c.c.

The detailed structure is actually f.c.t. (face-centered tetragonal), where the expan-

sion parallel to the ﬁlm plane causes compression along the normal direction. This type

of distortion is very common, occurring in the opposite sense for Ge/Si(001) as dis-

cussed in section 7.3.3. In the magnetic case, the tetragonality induces uniaxial anisot-

ropy favoring perpendicular magnetization, which overcomes the shape eﬀects favoring

parallel alignment, if the ﬁlm is thin enough. The particular system Fe/Cu(001) is in

fact rather complicated, because in deposition even at room temperature, we can get

exchange diﬀusion of Fe into the Cu, since, on surface energy grounds, the Cu wants

to cover the Fe layer. There are now several similar examples (Fe/Ag, Fe/Au, Co/Cu,

etc.), which have been seen by Auger spectroscopy, STM and other methods. The

extreme sensitivity of the magnetism to the exact lattice parameter and micro-struc-

tural condition of the ﬁlm means that there are (too many) contradictory results in the

literature. These points have started to become clear in recent research papers; they are

discussed further here in sections 5.5.3 and 8.3.

6.3.3 Magnetic surface techniques

Investigation of magnetic surfaces and thin ﬁlms proceeds at two levels: structural and

microstructural examination can be done using the same techniques as for non-mag-

netic materials, as described in chapter 3, where some relevant examples were given.

Some techniques which are speciﬁc to magnetism are described here in outline. These

include optical rotation (Faraday and Kerr eﬀects plus magnetic circular dichroism

(MCD)) and spin-polarized electron techniques. For analysis of domain structures,

several microscope based methods have been developed which display magnetic con-

trast. These include SEMPA, SMOKE microscopy, TEM (Lorentz or holography,

described in the last section), spin-polarized LEEM and magnetic force microscopy

(MFM), which are explained below.

Optical techniques work in magnetic materials via the rotation of the plane of polar-

ized light. The dielectric constant « is a tensor, with oﬀ-diagonal terms of the form

6i«

, in addition to the usual diagonal terms, so that right- and left-handed circularly

polarized light behave diﬀerently. The eﬀects are called the Faraday eﬀect in transmis-

sion and the Kerr eﬀect in reﬂection. The most commonly used technique is called

MOKE (magneto-optic Kerr eﬀect) and the acronym SMOKE is used when this tech-

nique is applied to surfaces. Depending on the light polarization with respect to the

magnetization of the sample, one can measure diﬀerent Kerr signals which have com-

ponents perpendicular and parallel to the sample. By varying the magnetic ﬁeld cycli-

cally, one can obtain hysteresis loops to characterize the magnetic state of the sample.

6.3 Magnetism at surfaces and in thin ﬁlms 213

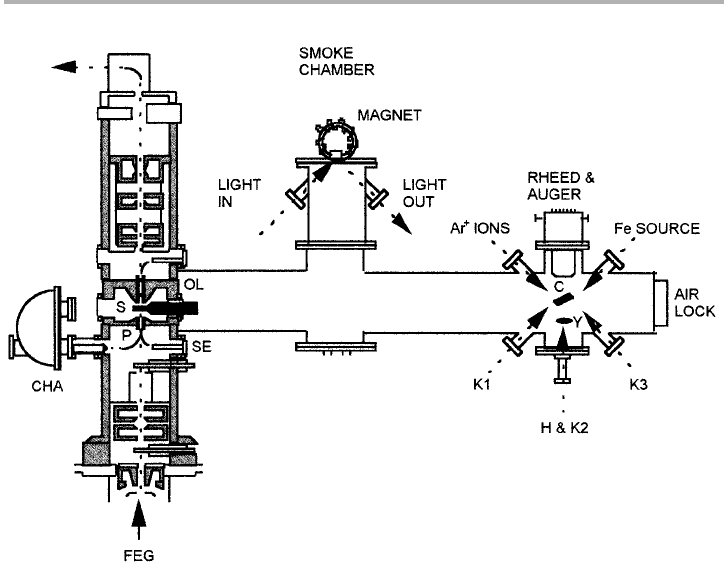
A diagram of the geometry of the preparation chamber of MIDAS at Arizona State

University, and typical Kerr loops, are shown in ﬁgures 6.17 and 6.18. This conﬁgura-

tion has enabled in situ comparisons of structural and magnetic properties of a range

of thin ﬁlm magnetic systems.

Magnetic circular dichroism (MCD) is a powerful recent technique which is a cross

between photoemission and MOKE. By using spin-orbit split core levels, separated by

10 eV or more, the magnetism of thin ﬁlms, including internal interfaces, can be

studied. The core levels are speciﬁc to particular elements, and the rotation of the plane

of polarization is speciﬁc to the magnetism at the sites of these elements. A special

merit of MCD is that it enables spin-speciﬁc and element-speciﬁc measurements to be

made concurrently (Bader & Erskine 1994). This is particularly powerful, e.g. (a) in fer-

rimagnetic systems where diﬀering spin sublattices have diﬀerent orientations; (b) in

trilayers and multilayers such as Fe/Cr/Fe(001), where the magnetic alignment is

diﬀerent in the various layers (Idzerda et al. 1993). MCD is typically performed using

214 6 Electronic structure and emission processes

Figure 6.17. The MIDAS column and preparation chamber arranged for magnetic studies.

The column shows the position of the sample (S), objective lens (OL), electron parallelizers

(P) and secondary electron detector (SE), all of which are shown in more detail in ﬁgure 3.24,

plus the ﬁeld emission gun (FEG). The sample can be transported from the airlock to the

sample preparation station, which has multiple ports used as shown plus those for sample

heating (H) and extra Knudsen cell evaporators (K1–K3); the YAG screen (Y) is for viewing

the RHEED pattern. After preparation, the copper sample (C) can be transported to the

SMOKE station before being examined by high resolution SEM and analysis (after Heim et

al. 1993, reproduced with permission).

a synchrotron radiation source, and is a powerful application of display analyzers, as

shown in ﬁgure 3.9(d) (Daimon et al. 1995).

Electron spectroscopy can be used to study magnetic domains. Electrons emitted

from a magnetic material are spin polarized, because the spin up and spin down bands

are populated diﬀerently. This is a strong eﬀect for low energy secondary electrons,

where the polarization can reach 640%, with ⬃620% for Fe and ⬃610% for Co at

6.3 Magnetism at surfaces and in thin ﬁlms 215

Figure 6.18. Polar and longitudinal hysteresis loops from Fe/Cu(001) grown and measured at

room temperature, taken with the SMOKE setup in MIDAS shown in ﬁgure 6.17 with an

angle of incidence of 45°: (a) and (b) 2.1 ML, no remanent magnetization; (c) and (d) 3.5 ML,

remanent, mostly out of plane; (e) and (f) 4.7 ML remanent, in plane; (g) and (h) 10 ML, non-

magnetic f.c.c. Fe ﬁlm (after Hembree et al. 1994, reproduced with permission).

higher energies, where the spectrum reﬂects the polarization of the valence band

(Kirschner 1985, Landolt 1985, Hopster 1994). Combined with SEM, this has lead to

the development of scanning electron microscopy with polarization analysis

(SEMPA). The extra element is the addition of a spin polarization detector. These

detectors detect left–right (or up–down) asymmetries caused by spin-orbit (Mott) scat-

tering, typically in a heavy target such as gold. Clear views of the domain structure,

completely diﬀerent from the normal SEM image of the same area, can be obtained as

shown in ﬁgure 6.19 (Hembree et al.1987; Scheinfein et al. 1990).

There are several versions of such detectors, and the polarization P is determined by

an algorithm of the form

P5C(L2R)/(L1R), (6.15)

using the two signals L and R. The sensitivity of this technique depends on the eﬀective

Sherman function S

eﬀ

⬃0.1–0.3 typically, increasing with incident electron energy in

the range 10–100 keV, and the constant C⬃S

eﬀ

. The ﬁgure of merit for the detector

is proportional to the ratio of the detected to the incident current (I

)·S

eﬀ

which is

typically small (,10

). Typically, magnetic eﬀects can be enhanced by reversing the

ﬁeld and taking diﬀerence signals, but this is not always necessary if one is prepared to

live with an oﬀset signal arising from possible alignment errors in the detector system.

Spin-polarized AES is also possible using an electron spectrometer in addition to a

spin-polarized detector. As may be imagined, SPAES signal levels are very small, and

long collection times are required to achieve an adequate SNR.

The above techniques use unpolarized electron sources, but spin polarized sources

can be made using circularly polarized photoemission from spin-polarized valence

bands. The most commonly used source is p-type GaAs(001), selectively exciting the

heavy hole (p

3/2

) band with 1.4 eV photons. This puts spin-polarized electrons into the

conduction band. The trick is then to activate the surface to negative electron aﬃnity,

by coating the surface with a Cs/O layer. This strongly reduces the work function of

GaAs, such that the bottom of the conduction band is above the vacuum level; elec-

trons therefore spill out into the vacuum, and are suﬃciently intense to form a source,

even for a microscope. Comprehensive reviews of this technique have been given by

Pierce et al. (1980) and Pierce (1995).

Spin-polarized LEEM is a technique which is being developed for magnetic materi-

als. Phase sensitive detection to eliminate unwanted background signals is possible, by

modulating the laser polarization, and detecting the electrons in synchronism. This

work is in its infancy at present, but progress has been reviewed (Bauer 1994); more

recent results are given by Bauer et al. (1996). An example of a SPLEEM image from

the last reference is shown in ﬁgure 6.20.

Magnetic force microscopy is a development of AFM which measures the ﬁeld gra-

dient above ferromagnets; the force on a magnetic moment

in the z-direction

/dz, and lateral force measurements are also possible. Typically, a cantilever

with a etched Si tip of radius r ⬃10 nm is sputter coated with a ferromagnetic material.

If the coercivity is high, this allows the magnetization distribution of the tip to remain

ﬁxed as the ﬁelds on the sample are changed. The ﬁeld emanating from the tip falls oﬀ

216 6 Electronic structure and emission processes