Venables J. Introduction to Surface and Thin Film Processes

Подождите немного. Документ загружается.

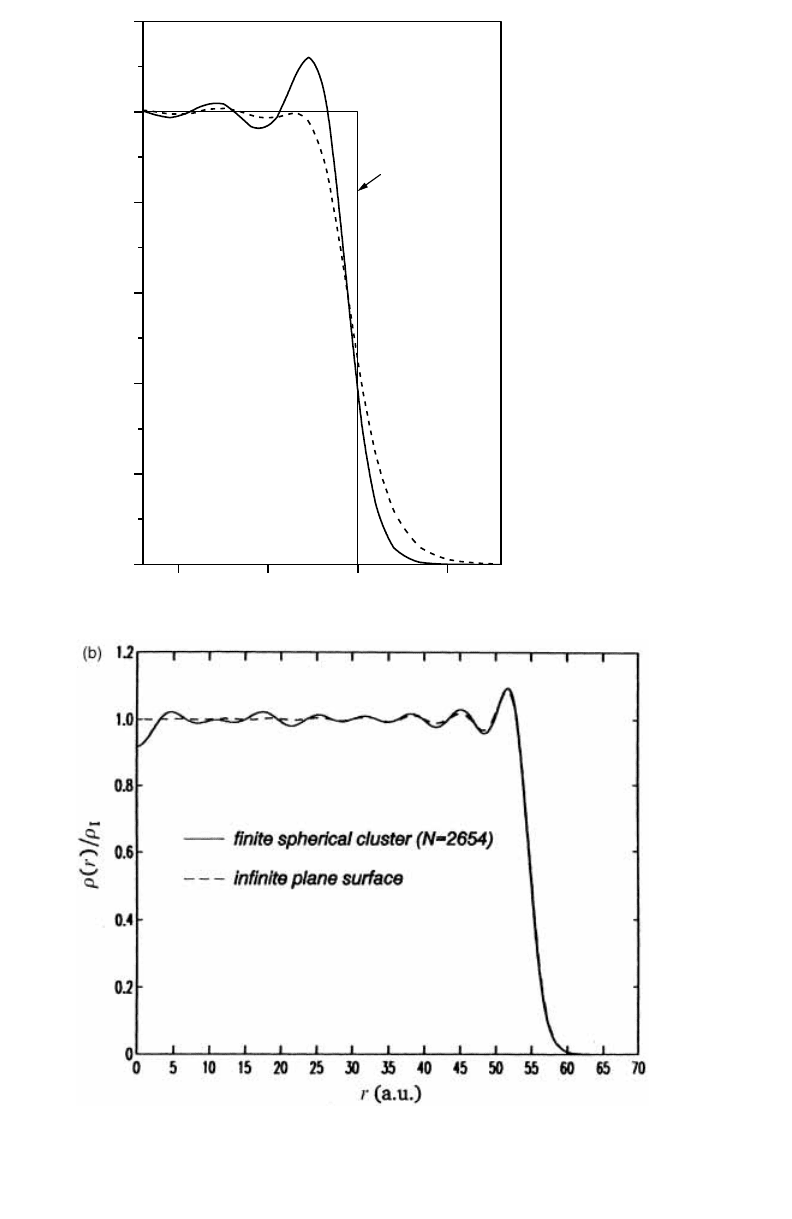
Figure 6.2. Electron density at a metal surface in the jellium model: (a) Lang & Kohn (1970)

for r

52 and 5; (b) comparison between a spherical cluster of 2654 simulated Na atoms

53.96) and a planar surface for r

54 (after Genzken & Brack 1991, and Brack 1993,

reproduced with permission).

–1.0 –0.5 0.0 0.5

0.0

0.2

0.4

0.6

0.8

1.0

1.2

(a)

Positive

background,

–

for

= 2

–

for

= 5

Distance

(Fermi wavelengths)

Charge density (relative to bulk)

(or dip) varies with electron energy and is dominated by the highest occupied states

which vary with the exact cluster size, whereas the oscillations close to the surface are

independent of such details.

The oscillations in the electron density are called Friedel oscillations; these occur

when a more or less localized change in the positive charge density (the discontinuity

at the jellium model surface being an extreme case) is coupled with a sharp Fermi

surface. In other words, they are a feature of defects in metals in general, not just sur-

faces, and are an expression of Lindhard screening, which is screening in the high elec-

tron density limit. Screening in metals is so eﬀective that there are ripples in the

response, corresponding to overscreening.

Recently, these electron density oscillations have been seen dramatically in STM

images both of surface steps, and of individual adsorbed atoms on surfaces, reported

in several papers from Eigler’s IBM group. By assembling adatoms at low temperature

into particular shapes, these ‘quantum corrals’ can produce stationary waves of elec-

tron density on the surface which are sampled by the STM tip, and the corresponding

Friedel oscillations are energy dependent; two examples from a circular assembly of 60

Fe atoms on Cu(001) are shown in ﬁgure 6.4.

Whether or not these eﬀects can be explained in detail as yet (Fe and Cu are both

188 6 Electronic structure and emission processes

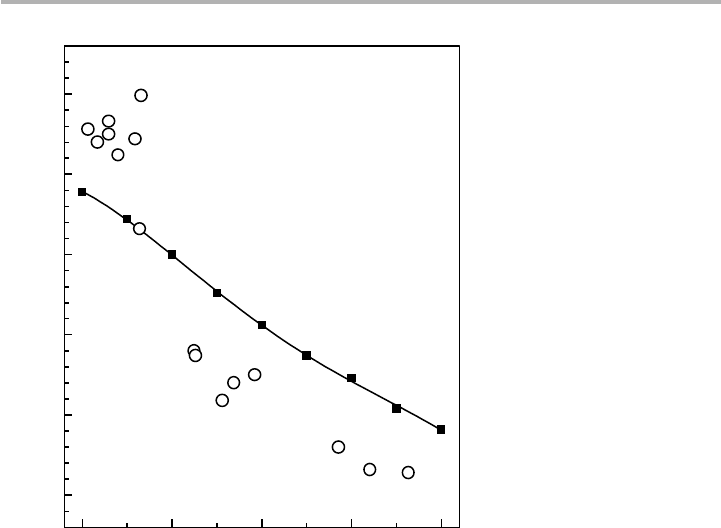
Figure 6.3. Work functions in the jellium model (full squares, Lang & Kohn 1971), compared

with experimental data for polycrystalline alkali and alkaline earth metals (open circles:

Michaelson 1977). The elements plotted are after Lang (1973) and the solid line fourth-order

polynomial ﬁt to these points has been added.

23456

2.0

2.5

3.0

3.5

4.0

4.5

Work function,

(eV)

radius,

(a.u.)

transition metals with important d-bands), these oscillations are present in free elec-

tron theory. To see how such eﬀects arise, one needs to do as simple a calculation as

possible, and try to understand how the physics interacts with the mathematics. The

calculation done by Lang & Kohn goes roughly as follows, using ﬁgure 6.5 as a guide.

Consider pairs of states, ordered by their k-vector perpendicular to the surface, k

and 2k. Their wavefunction is

⬃

(z) exp i(k

x1k

y), and when 6k are combined

to vanish in the vacuum (outside the surface),

(z)⬃sin(kz -

), where

is a phase

factor, dependent on k

, since the origin doesn’t have to be exactly at z50. Draw a

Fermi sphere, radius k

, with the k-axis (perpendicular to the surface) as a unique axis,

as in ﬁgure 6.5. Make a slice at k,dk thick; the density of states g(k) is just the area of

this slice which is p(k

). Now we can write

5n(z)5p

兰

g(k)|

dk, (6.3)

where the limits of integration are 0 and k

, and with a bit of manipulation you should

get the result

n(z)5n¯ [113cos{2(k

)}/(2k

1O(2k

], (6.4)

6.1 The electron gas 189

Figure 6.4. A ‘quantum corral’ of 60 Fe atoms assembled and viewed on Cu(001) by STM at

4K. The tip imaging parameters are (a) V

5110 mV and (b) 210 mV, with current I51 nA

(after Crommie et al. 1995, reproduced with permission).

(a) (b)

Figure 6.5. (a) Cross section of the free electron Fermi surface, radius k

; (b) the combination

of traveling wave states 6k near a surface. See text for discussion.

(a)

(b)

(2k)()

–1

where the O-notation means ‘of order (2k

’. Here n¯ is the electron density in the

bulk; the symbols n¯ and

are used interchangeably. The point which is speciﬁc to 2D

surfaces and interfaces is the dependence on (2k

. For impurities or point defects,

the result is O(2k

, which is due to 3D geometry. For corrals on the surface with

cylindrical geometry, we encounter various types of Bessel function, for the same

reasons as in chapter 5. In scattering/perturbation theory terms, the characteristic

length, (2k

)

, is due to scattering across the Fermi surface without change of energy.

The same length occurs in the theory of superconductivity and charge density waves;

these features can be explored further via problem 6.1.

It is interesting that the jellium model also gives, though not so impressively, values

for the surface energy of the same metals as shown later in ﬁgure 6.10. The agreement

is again excellent for the heavier alkali metals, but fails dramatically for small r

. This

arises from the need to include the discreteness of the positive charge distribution asso-

ciated with the ions, a point which was recognized in Lang & Kohn’s original paper.

With a suitable choice of pseudopotential, agreement is much improved (Perdew et al.

1990, Kiejna 1999).

6.1.2 Beyond free electrons: work function, surface structure and energy

There have been many developments since Lang & Kohn to extend this approach, ﬁrst

to s-p bonded metals and then to the complications of transition metals involving d-

electrons, and in the case of the rare earths, f-electrons as well. The d-electrons give an

angular character to the bonding, often resulting in structures which are not close-

packed, e.g. b.c.c. (Fe, Mo, W, etc.) or complex structures like

-Mn. This is in contrast

to s-p bonded metals which typically are either f.c.c. or h.c.p. There are many chal-

lenges left for models of metallic surfaces.

To start we need a few names of the methods, for example ‘nearly-free electron’

method, pseudopotentials, orthogonalized plane waves (OPW), augmented plane

waves (APW), Korringa–Kohn–Rostoker (KKR), tight-binding, etc. These long-

standing methods are described by Ashcroft & Mermin (1976). For surfaces, an intro-

ductory account of electronic structure is given by Zangwill (1988), which contrasts

with a highly detailed version from Desjonquères & Spanjaard (1996). Typically tight-

binding (where interatomic overlap integrals are thought of as small) is taken as the

opposite extreme to the nearly free electron model (where Fourier coeﬃcients of the

lattice potential are thought of as small). However, this is more apparent than real, in

that both pictures can work for arbitrarily large overlap integrals or lattice potentials;

the only requirement is that the basis sets are complete for the problem being studied.

This of course can lead to some semantic problems: methods which sound diﬀerent

may not in fact be so diﬀerent; in particular, when additional eﬀects are included they

are almost certainly not simply additive.

The basic feature caused by including the ions via any of these methods is that the

electron density near the surface is now modulated in x and y with the periodicity of

the lattice; an early calculation which shows this for the lowest atomic number metal

lithium is given in ﬁgure 6.6. So there are now two length scales in the problem which

190 6 Electronic structure and emission processes

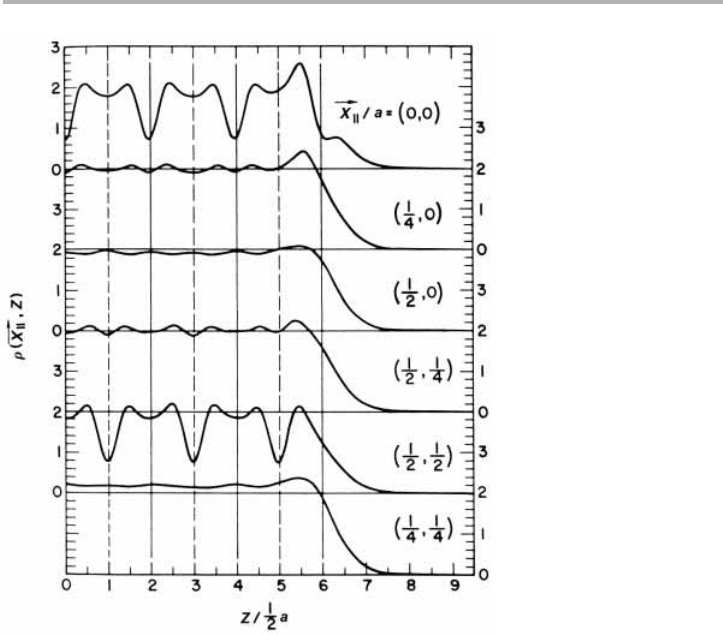
compete; surface states have oscillation periods with no simple relation to the lattice

period in the z-direction.

Contrary to the free electron starting point, it has more recently proved fruitful to

consider models based on wavefunctions relatively localized in real, rather than recip-

rocal, space, and to construct interatomic potential functions arising from atomic-like

entities interacting with the electron gas in which the ‘atom’ is embedded (Sutton 1994,

Pettifor 1995, Sutton & Balluﬃ 1995). The resulting methods are known as embedded

atom models (EAM) or eﬀective medium theories (EMT); in these models the embed-

ding energy DE is expressed in terms of the cohesive function E

(n), as

DE5E

(n)1DE

, (6.5)

where the correction energy DE

diﬀers between the various schemes, but is relatively

small.

The cohesive function E

(n) is a function of the homogeneous electron gas density n

in which the atom is embedded (Jacobsen et al. 1987, Jacobsen 1988, Nørskov et al.

1993). The cohesive energy, and the component E

(n¯) at the optimum density n¯ is

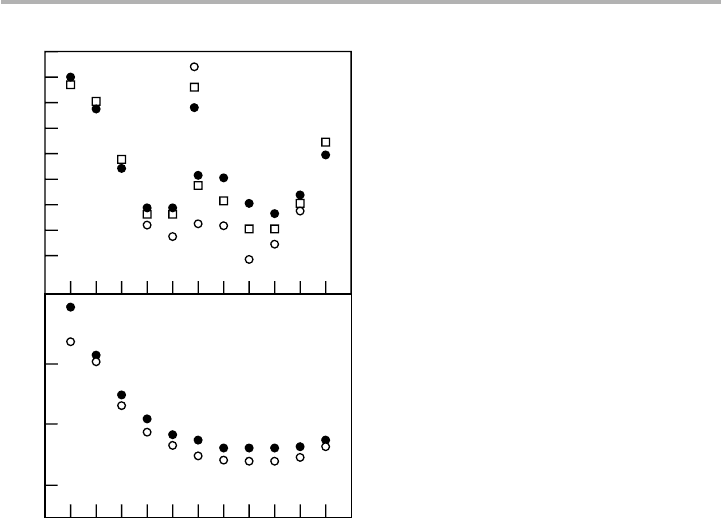
shown for the 3d transition metals in ﬁgure 6.7. A major eﬀect of these models is to

6.1 The electron gas 191

Figure 6.6. Valence electron density at several x

points for Li(001) in a pseudopotential

calculation (from Alldredge & Kleinman 1974, reproduced with permission, after Appelbaum

& Hamann, 1976).

show clearly that metallic binding is strongly non-linear with coordination number.

The ﬁrst ‘bonds’ to form are strong, and get progressively weaker as extra metal atoms

are added to the ﬁrst coordination shell. Some of these eﬀects were exhibited by the

experimental examples described in section 5.4. There are many subtleties in the 3d

series resulting from magnetism; here the overall cohesion peaks before and after the

middle of the transition series, unlike the 4d and 5d series, where cohesion from the d-

bands peaks in the middle. Note that this particular calculation does not include spin-

correlation eﬀects, but some of these are discussed in relation to magnetism in section

6.3.

Many metal surface relaxations and reconstructions are due to competing electronic

and vibrational eﬀects of a quite complex kind. For example, reconstructions of tran-

sition metals are often subtle, such as the W(001)231 and the ‘almost 231’ incom-

mensurate Mo(001) structures at low temperatures mentioned in section 1.4.3. These

structures are driven by (angular) bonding instabilities at low temperature and by

anharmonic lattice dynamics at high temperature (Inglesﬁeld 1985, Estrup 1994,

Titmus et al. 1996). F.c.c. noble metal surfaces can be strongly aﬀected by their d-elec-

trons, interacting with the ions and the other electrons. Although Ag(111)(131) is

unreconstructed, Au(111) has a uniaxially compressed herringbone (roughly 2331)

192 6 Electronic structure and emission processes

Figure 6.7. Calculated cohesive energies and the equilibrium radius r

for the 3d transition

series, comparing eﬀective medium theory (EMT) (open circles) with KKR methods

(Morruzzi et al. 1978, closed circles). The modiﬁed EMT (open squares) corresponds to EMT

applied at the density given by the KKR method (Jacobsen et al. 1987, and Jacobsen 1988;

redrawn with permission).

K Ca Sc Ti V Cr Mn Fe Co Ni CuK Ca Sc Ti V Cr Mn Fe Co Ni Cu

Radius, (a.u.)

Radius,

(a.u.)r

Cohesive ener

gy (eV/atom)

Cohesive ener

gy (eV/atom)

EMT

Modified EMT

Moruzzi et al.

EMT

Modified EMT

Moruzzi et al.

reconstruction, Au(001) has a quasi-hexagonal surface layer giving a (roughly 2035)

diﬀraction pattern (Van Hove et al. 1981, Barth et al. 1990), and Pt(111) has a 737

reconstruction which can be removed by depositing Pt adatoms (Needs et al. 1991,

Bott et al. 1993). This last case shows that the surface structure and lattice parameter

of a metal can be a function of the supersaturation D

of its own vapor, and that

adatoms and surface reconstructions can change the surface stress. This possibility is

also well known from adsorption studies of rare gases on graphite, as discussed in

section 4.4.

An increasing number of theorists are suﬃciently practical and public-spirited that

they collaborate closely with experimentalists, and make their computer codes avail-

able to others for work on speciﬁc problems. It is a welcome recent development that

theorists have addressed the problem of ‘understanding’. By this I mean that they

acknowledge that the ‘true’ solution is obtained by keeping all the terms in the

Schrödinger equation that they can think of, but that this doesn’t necessarily help one

understand trends in behavior, or help one make predictions. Pettifor (1995), for

example, starts with a quote from Einstein: ‘As simple as possible, but not simpler’.

This is excellent: with such an attitude there is real prospect that we can ‘understand’

a higher proportion of theoretical models than we would be able to otherwise.

Increasingly what counts is the speed of the computer code; if this speed scales with

a lower power of the number, N, of electrons in the system, then more complex/larger

problems can be tackled; O(N) methods are in! For example, because the interactions

between atoms and the electron gas are parameterized initially, EMT calculations are

fast enough that they can be used to simulate dynamic processes such as adsorption,

nucleation or melting on metal surfaces; here an approximate electronic structure cal-

culation is being done for each set of positions of the nuclei, i.e. at each time step

(Jacobsen et al. 1987; Stolze 1994, 1997). This requires computer speeds that would

have been inconceivable just a few years ago. It is now feasible to download EMT pro-

grams from a website in Denmark (see Appendix D) in order to run them for a class

project in Arizona! There are real possibilities for experiment–theory collaborations

here which were impractical just a few years ago.

6.1.3 Values of the work function

There are several methods of measuring the work function, as described by Woodruﬀ

& Delchar (1986, 1994), by Swanson & Davis (1985) and by Hölzl & Schulte (1979)

amongst others. The work function varies with the surface face exposed, as shown for

several elemental solids in table 6.2. Note that for b.c.c. metals, the surfaces decrease

in roughness in the order (111), (100), (110) presented, whereas for f.c.c. the same order

corresponds to an increase in roughness. These variations are responsible for several

interesting eﬀects, as described here and in the next section.

A polycrystalline material, with diﬀerent faces exposed, gives rise to ﬁelds outside the

surface, referred to as patch ﬁelds. Such ﬁelds are very important for low energy elec-

trons or ions in vacuum, and can thereby inﬂuence measurement accuracy in surface

experiments. Molybdenum is often used for such critical parts of UHV apparatus,

6.1 The electron gas 193

194 6 Electronic structure and emission processes

Table 6.2. Experimental work functions for metals assembled by Michaelson (1977),

compared with calculations by Perdew, Tran & Smith (1990; PTS), Skriver &

Rosengaard (1992; SR) and Methfessel, Hennig & Scheﬄer (1992; MHS), plus

others as indicated in the last column

Model

Metal/ Face Experiment* Model Model (MHS)

structure {hkl} (eV) (PTS) (SR) 1 others*

Li 111 2.90

b.c.c. 100 2.9 (poly) 2.92 3.15 3.03

110 3.09 3.33 3.27

Na 111 2.54

b.c.c. 100 2.75 (poly) 2.58 2.76 2.66

110 2.75 2.94 2.88

K 111 2.17

b.c.c. 100 2.30 (poly) 2.21 2.34 2.27

110 2.37 2.38 2.44

Cs 111 1.97

b.c.c. 100 2.14 (poly) 2.01 2.03 2.04

110 2.17 2.09 2.19

Al 110 4.06 3.81

f.c.c. 100 4.4160.03

3.62 4.50

111 4.24 3.72 4.54 4.09

Cu 110 4.48 4.48

f.c.c. 100 4.59 5.26

111 4.98 5.30

Ag 110 4.52 4.40 4.23

f.c.c. 100 4.64 5.02 4.43

111 4.74 5.01 4.67

Au 110 5.37 5.40

f.c.c. 100 5.47 6.16

111 5.31 6.01

Nb 111 4.36

b.c.c. 100 4.02 3.68

110 4.87 4.80 4.66

Mo 111 4.55

b.c.c. 100 4.53 4.49

110 4.95 5.34 4.98

W 111 4.47

b.c.c. 100 4.63

110 5.25 5.62

Note: *Error bars and other calculations by: (a) Inglesﬁeld & Benesh (1988); (b) Perdew

(1995).

because the work function doesn’t vary more than 0.4 V between the low index faces

(table 6.2), whereas Nb and W, which are otherwise similar, have variations of around

0.8 V.

The origin of this face-speciﬁc nature of the work function can be seen qualitatively

by considering jellium again. First, we can see from ﬁgures 6.1 and 6.2 that the nega-

tive charge spills over into the vacuum, causing a dipole layer, whose dipole moment is

directed into the metal. Now we use Gauss’ law and show that

DV(volts)5

5pN/

, (6.6)

where the sheets of charge, surface charge density

, are separated by a distance d.To

get an idea of how big the potential change is, think of each atom on the surface

(Nm

) having a charge of 1 electron separated by 0.1 nm (1 ångström). With N523

, p51.6310

229

Cm, and

58.854310

212

, we get DV536.14 V. This

value is perhaps 2–5 times as large as most voltage (energy) diﬀerences between the

vacuum level and the bottom of the valence band (which is also the conduction band

in monovalent metals).

So a charge separation of ,0.5Å is needed to produce the desired eﬀect. Is it a coin-

cidence that this is the same order of magnitude as the Bohr radius, a

50.0529 nm?

Not really: the reasons for both eﬀects, the spill over of electrons due to the need to

reduce kinetic energy, are the same! This is, of course, a zero order argument: to get the

numbers right we have to go back to exchange and correlation energies, and the details.

However, models may contain rather arbitrary parameters. For example, the ‘corruga-

tion factor’ introduced into the ‘structureless pseudopotential model’ (Perdew et al.

1990) sounds rather dubious, although it moves the model in the right direction

(Perdew 1995). Brodie (1995) has proposed a model, building on the idea of corruga-

tion, which is ‘too simple’ in Einstein’s sense; this model should be ignored since it is

incapable of further elaboration.

While on this subject, we can note the unit to describe dipole moments, the Debye

(D). This is 10

218

esu·cm53.33310

230

Cm. Thus 1 electron charge31Å54.81 D.

Adsorbed atoms change the work function considerably, but only alkalis give rise to

dipole moments this large; for example Cs adsorbed on W(110) at low coverages has

been calculated to have a dipole moment of at least 9D (see e.g. table 2.2. in Hölzl and

Schulte 1979); in this case the single electron charge distribution would be shifted by

about d50.2 nm. This simple picture is illustrated in ﬁgure 6.8(a), and corresponds to

(partial) ionization of the alkali, a model ﬁrst introduced by Langmuir in 1932 and

developed by Gurney in 1935. But we need to be careful about inclusion of the image

charge, and the nature of bonding, which varies with coverage and is the subject of

ongoing discussion (Diehl & McGrath 1997).

The same arguments about electron spillover tell us that stepped, or rough surfaces

will have lower work function than smooth surfaces, due to dipoles associated with

steps, pointing in the opposite direction to the dipole previously considered for the ﬂat

surface. A schematic (top view) of this situation, referred to sometimes as the

Smoluchowski eﬀect after a 1941 paper, is shown in ﬁgure 6.8(b). Experiments on

vicinal surfaces, close to low index terraces, do indeed show that the work function

6.1 The electron gas 195

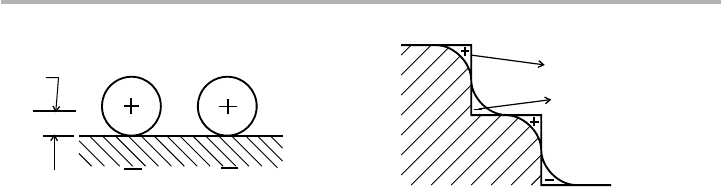
decreases linearly with step density, as shown in ﬁgure 6.9; this implies that there is a

well deﬁned dipole moment per ledge atom, around 0.3 D for steps parallel to [001] on

W(110) and varying with step direction on Au and Pt(111) surfaces (Krahl-Urban et

al. 1977; Besocke et al. 1977; Wagner 1979).

Fascinatingly, work function changes as a function of temperature can be used to

deﬁne 2D solid–gas phase changes via these same eﬀects. An adatom has a dipole

moment which depends both on its chemical nature and on its environment. In a solid

ML island the dipole moment per atom is considerably smaller than in the 2D gas. This

eﬀect has been used to map out the gas–solid phase boundary for Au/W(110) at high

temperatures (Kolaczkiewicz & Bauer 1984). Phase changes in adsorbed layers are dis-

cussed in more detail in chapter 4.

6.1.4 Values of the surface energy

While the work function is a sensitive test of electronic structure models, particularly

exchange and correlation, surface energies are sensitive tests of our understanding of

cohesion. Surface energies clearly increase, in general, with sublimation energies, and

this has led to many studies trying to embody such relationships into universal poten-

tial curves, or into other semi-empirical models (Rose et al. 1983, deBoer et al. 1988).

But the eﬀective medium and density functional models have proven to be more

durable, and we may well now have arrived at the point where these models are more

accurate than the experiments, which were almost all done a long time ago on poly-

crystalline samples, sometimes under uncertain vacuum conditions. An example of a

microscope based sublimation experiment for Ag, which has stood the test of time, and

which agrees with recent calculations within error, is that by Sambles et al. (1970).

Some experimental and theoretical values for a range of metals are given in table 6.3.

As in the case of the work function, the starting point for models of alkali and other

s-p bonded metals has been the jellium model. As was shown in the original Lang &

Kohn papers, jellium has an instability at small r

values, which is due to the neglect of

the ion cores. This topic has been pursued by Perdew et al. (1990), Perdew (1995) and

Kiejna (1999), who have been interested in exploring the simplest feasible pseudopo-

tential models for such metals, and in particular obtaining trends in calculations as a

196 6 Electronic structure and emission processes

Figure 6.8. Origins of face- and adsorbate-speciﬁc work function: (a) dipoles due to charge

transfer from adsorbates; (b) top-view of a stepped surface showing smoothing of the charge

distribution around the steps (after Gomer 1961, and Woodruﬀ & Delchar 1986, redrawn with

permission).

(a) (b)

image chargesimage charges

+ve

-ve

charge