Venables J. Introduction to Surface and Thin Film Processes

Подождите немного. Документ загружается.

Kelly, M.J. (1995) Low-dimensional Semiconductors (Oxford University Press) chapters

1–3.

Liu, W.K. & M.B. Santos (Eds.) (1999) Thin Films: Heteroepitaxial Systems (World

Scientiﬁc).

Lüth, H. (1993/5) Surfaces and Interfaces of Solid Surfaces (2nd/3rd Edn, Springer)

chapter 6.

Mönch, W. (1993) Semiconductor Surfaces and Interfaces (Springer) chapters 7–18.

Pettifor, D.G. (1995) Bonding and Structure of Molecules and Solids (Oxford University

Press) chapters 3 and 7.

Sutton, A.P. (1994) Electronic Structure of Materials (Oxford University Press) chap-

ters 6 and 11.

Sutton, A.P. & R.W. Balluﬃ (1995) Interfaces in Crystalline Materials (Oxford

University Press) chapter 3.

Tsao, J.Y. (1993) Materials Fundamentals of Molecular Beam Epitaxy (Academic).

Yu, P.Y. & M. Cardona (1996) Fundamentals of Semiconductors: Physics and Materials

Properties (Springer) chapter 2.

Zangwill, A. (1988) Physics at Surfaces (Cambridge University Press) chapter 4.

Problems and projects for chapter 7

Problem 7.1. Band structures of Si, Ge and GaAs

Look up the calculated band structures of bulk Si, Ge and GaAs, and explain the

meaning of the following terms in relation to these three solids:

(a) the existence of a direct versus an indirect band gap, and the position of the con-

duction band minimum;

(b) spin-orbit splitting and the diﬀerences between light and heavy holes;

Project 7.2. Band structures in tight binding models

Tight-binding pseudopotential models of tetrahedral semiconductors such as Si or Ge

treat the valence s- and p-electrons as moving in the potential ﬁeld of the nuclei plus

closed shell electrons. Consult selected references for section 7.1, and show one of more

of the following.

(a) That eight electrons are required to describe the system, resulting in the need to

diagonalize an 838 matrix to solve for the band structure as a function of the wave

vector k.

(b) That a possible approach to this problem is to use sp

hybrid states as the basis set,

formed by linear combinations of 1 s- and 3 p-electrons as in equation (7.1). Find

the relations between the overlap (or hopping) integrals expressed in the s, p

system and the sp

system. What is the potential advantage of the sp

basis?

Problems and projects for chapter 7 257

or other of these basis sets, and particular values of the matrix elements, using a

matrix diagonalization package, display your results graphically, and compare

your results to the literature.

(d) That the simplest model of band structure associated with the 231 reconstruction

on Si or Ge(001) involves ﬁxing the atoms below the surface plane in their bulk

positions, and constructing a matrix as a function of wavevectors, k

, k

in the

plane of the surface, and k

perpendicular to the surface, again involving an 838

matrix, but now with some of the matrix elements set equal to zero. What is needed

in addition to calculate the equilibrium position of the surface atoms and the

resulting surface band structure and surface states?

Problem 7.3. Removal of long range ﬁelds in polar crystals via surface

reconstruction

Draw the planar structure of GaAs to scale, viewed perpendicular to [111], and

(a) identify the planes containing Ga and those containing As, and the [111] versus the

] directions.

If both Ga and As assume the sp

conﬁguration,

(b) use Gauss’s law to work out the average internal electric ﬁeld along [111]. Note that

a suitable choice of unit cell for the Gaussian surface may convince you that all the

long range ﬁeld is due to the surface layers.

7.4) plus the same numbers of As atoms from the (1

) B face removes this inter-

nal ﬁeld.

Project 7.4. Adatoms, surface vibrations, roughening and melting

transitions on Si and Ge

The melting temperature and latent heat of melting of Si and Ge, Fe and Ag are listed

by Honig & Kramer (1969) as in table 7.4.

(a) From these data evaluate the entropy of melting for the four elements, using

Appendix C to express the results in units of k/atom.

(b) Do a literature search to ﬁnd out whether any of the low index surfaces of these

258 7 Semiconductor surfaces and interfaces

Table 7.4. Melting temperatures and enthalpies of metals and semiconductors

Si Ge Fe Ag

Atomic mass (u) 28.1 72.6 55.8 107.9

(K) 1685 6 3.0 1210.4 1809 1234

(kcal/mole) 12.0 6 1.0 8.83 3.3 6 0.1 2.7 6 0.1

elements are known actually to undergo roughening or melting transitions, and if

so under what conditions.

600 K, but experiments at T51300 K seem to suggest that their free energies are

roughly equal (Bermond et al. 1995). Using the tables in the text, what can you

deduce about the diﬀerence in surface excess entropies between the two faces?

Estimate the surface excess entropy involved (in k/atom units), and compare

with the melting entropy, in the following situations, using equations from section

4.2 as appropriate.

(d) We have a certain concentration of ad-dimers on Si(001). Evaluate the conﬁgura-

tional entropy at T51300 K, assuming that the concentration shown in ﬁgure 7.10

corresponds to ad-dimers. What is the additional entropy if these ad-dimers are

moving around as a 2D gas?

(e) We have asymmetric dimers on Si or Ge(001), each of which can be either up or

down with equal probability. Show that this answer must also represent an upper

limit to the entropy due to a single step moving freely across the surface. This is a

(very rough) approximation to the entropy involved in the roughening transition,

discussed in more detail by Desjonquères & Spanjaard (1996, chapter 2).

(f) The amplitude of z-motion of the surface atoms is increased from say 0.01 to 0.05

nm when the p232 or c432 ordered dimer phases on Si(001) disorder into to the

‘231’ (Shkrebtii et al.1995). Is this entropy the same as in (e) or are they additive?

Problems and projects for chapter 7 259

8 Surface processes in thin ﬁlm

devices

This chapter discusses surface and near-surface processes that are important in the

context of the production and use of various types of thin ﬁlm device. In section 8.1

the role of band bending at semiconductor surfaces is considered along with the impor-

tance, and the perfection, of oxide layers and metal contacts on silicon surfaces.

Section 8.2 describes models which have been developed to understand electronic and

optical devices based on metal–semiconductor and semiconductor–semiconductor

interfaces. Then section 8.3 describes conduction processes in both non-magnetic and

magnetic materials, and discusses some of the trends which are emerging in new tech-

nologies based on thin ﬁlms with nanometer length scales. The ﬁnal section 8.4 dis-

cusses chemical routes to manufacturing, including novel forms of synthesis and

materials development. The treatment in this chapter is rather broad; my aim is to

relate the material back to topics discussed in previous chapters, so that, in conjunc-

tion with the further reading and references given, emerging technologies may be better

understood as they appear.

8.1 Metals and oxides in contact with semiconductors

This section covers various models of metals in contact with semiconductors, and the

oxide layers on semiconductors. Such topics are important for MOS (metal–oxide–

semiconductor) and the widely used CMOS (complementary-MOS) devices. Models

in this ﬁeld have been extremely contentious, so sometimes one has felt that little

progress has been made. However, recent developments and some new experimental

techniques have shed light on what is happening.

8.1.1 Band bending and rectifying contacts at semiconductor surfaces

Band bending can occur just below free semiconductor surfaces, and when metals or

oxides come into contact with semiconductors. Models of this eﬀect are given in many

places; the major eﬀect is caused by the presence of surface states in the band gap,

which pins the Fermi level and induces band bending. As indicated in ﬁgure 8.1 for an

n-type semiconductor, the bands bend upwards towards the interface. This bending is

associated with a dipole layer beneath the surface corresponding to the depletion

260

region, where the n-type impurities are ionized, and the surface states are negatively

charged. For a p-type semiconductor, band bending is reversed and surface states are

charged positively, as indicated earlier in ﬁgure 1.23(a). If the semiconductor is in

contact with a metal, the Fermi level is ﬁxed by the metal, so that band bending or band

ﬂattening can be induced depending on changes from the previous surface state distri-

bution.

The main electrical eﬀects of this band bending arise from the asymmetry in the

current ﬂow under bias, as shown in ﬁgure 8.1. In the conduction band, the electron

energy distribution corresponds to the tail of the Fermi function, so that at the

Schottky barrier height

, the number of electrons above the barrier scales as

exp[2(q

/kT)], where q is the (eﬀective, positive) electron charge. In the equilibrium

case, when the Fermi levels are equal on both sides of the junction, the energy distri-

butions above the barrier must be the same, and the current ﬂow has to be zero, as indi-

cated in ﬁgure 8.1(a). However, under bias voltage V, there is current ﬂow. Using the

formulae for thermionic emission over the barrier (see section 6.2), we have a current

density J, given by

J5J

5A*T

exp[2(q

/kT)]{exp(qV/kT)21}, (8.1)

where the ‘Richardson constant’, A* for the barrier, depends on the details of band

structures and interface chemistry. The rectifying character of the contact is deter-

mined by the asymmetry with respect to 6V, shown schematically in ﬁgures 8.1(b) and

(c). For forward bias (positive V) the current J

can increase without limit, but under

reverse bias, the current is limited to a low constant value J

by the Schottky barrier

height

. For higher reverse bias, catastrophic breakdown can occur.

This topic has a very long history, starting with the discovery of rectifying proper-

ties by Braun in 1874, and the use of ‘cats’ whiskers’ as detectors in the early days of

radio (Mönch 1990, 1994). The two classical means of checking (8.1) are given by Sze

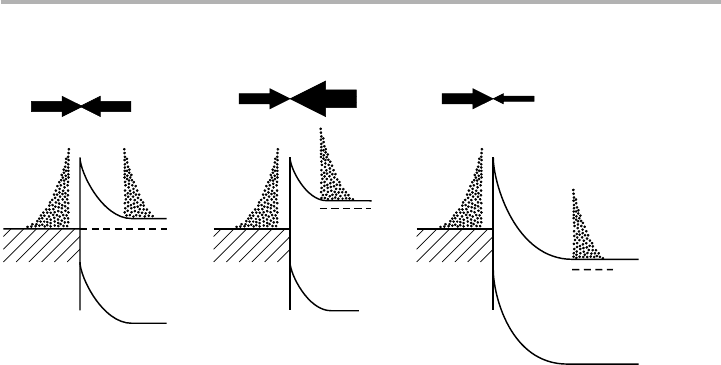
(1981). Figure 8.2 is a log–log plot of the forward bias current density J

as a function

8.1 Metals and oxides in contact with semiconductors 261

Figure 8.1. Band bending at the surface of an n-type semiconductor under diﬀerent biassing

conditions: (a) thermal equilibrium; (b) forward bias; (c) reverse bias.

(a)

(b) (c)

of V

, which gives a straight line whose slope is q/kT (Crowell et al. 1965). If q turns

out not to be equal to e, the charge on the electron, then so be it. Device engineers

replace q by q/n, where n is referred to as an ‘ideality factor’, with typical values of n5

1.02 to 1.04; i.e. the approximation that q5e is pretty good, but ‘non-ideality’ can be

used to cover several types of disagreement with this simple model. An Arrhenius plot

of the reverse barrier current I

, as (log I

) versus T

shown in ﬁgure 8.3, shows

that both A* and

for the important Al–Si diodes depend on processing conditions

(Chino 1973). This sensitivity to cookery has plagued the ﬁeld for a long time; both

recipes and theories have on occasion become so complex as to be completely unbe-

lievable. But, before discussing these points, the next topic is the width of the depletion

region.

262 8 Surface processes in thin ﬁlm devices

Figure 8.2. Logarithmic plot of forward current density J

versus forward voltage V

W–Si and W–GaAs diodes (from Crowell et al. 1965, after Sze 1981, reproduced with

permission).

8.1.2 Simple models of the depletion region

Models of the depletion region are well developed in the literature, and to dwell on

these here would take us too far from the topic of ‘surface processes’. The important

point to determine is the length scale over which (electron or hole) depletion is

observed, and to establish the connection with electrical and optical properties. The

key concept is screening, which was introduced brieﬂy in section 1.5, and the closely

related values of the (relative) dielectric constant

. Screening is very eﬀective in metals,

with screening lengths ⬃ (2k

)

, and moderately strong, but dependent on the doping

level, in semiconductors. It is weak in insulators, where for example it depends on ionic

defects in crystals such as NaCl, and photographic materials including AgBr. In

metals, Lindhard screening is required to describe the resulting Friedel oscillations (see

section 6.1), but in semiconductors and insulators, classical Thomas–Fermi screening

provides a suﬃcient description.

Consider a potential V(z) away from the surface, where the zero of V is in the bulk

8.1 Metals and oxides in contact with semiconductors 263

Figure 8.3. Arrhenius plot of the barrier current (I

) of Al–Si Schottky barrier diodes

under reverse bias for diﬀerent processing conditions (from Chino 1973, after Sze 1981,

reproduced with permission).

of the crystal, and an associated charge density

(z). This charge density may consist

of both ionized donors and acceptors, whose values are N

and N

respectively, and

the electron and hole density, n(z) and p(z), whose values are n

and p

in the bulk. In

the bulk, the charges have to be compensated, so that N

– N

2 p

. The elec-

tron and hole charge distribution is biased in the presence of V(z), which is diﬀerent

from zero near the surface, and gives

(z)51q[n

(exp(2qV(z)/kT)21) 2p

(exp(1qV(z)/kT) 21)]. (8.2)

Note that the positive sign arises because the donor and acceptor distributions stay the

same, while the electron and/or hole distribution responds to V(z); care is needed with

signs throughout this argument, which takes the electron to have q52e.

Equation (8.2) needs to be solved self-consistently, which is done within classical

electrostatics using the Poisson equation

V(z)/dz

(z)/

««

. (8.3)

This can be solved numerically, but is typically expressed within one of two limiting

approximations, for either n- or p-type semiconductors, i.e. when N

..N

or vice

versa. In the weak space charge approximation, we make a linear approximation to the

exponentials in (8.2) which gives

(z)5(n

or p

V/(

««

kT), (8.4)

where we use n

or p

for n- or p-type doping. This results in V(z)5V

exp (2z/L), where

is the potential at the surface; the screening length L is given by

(Lq)

««

kT)/(n

or p

). (8.5)

In the other limit we acknowledge that if V

is large compared to kT, then

(z) will

approximate to a step function, such that all the charges are ionized up to a depth d

below the surface, i.e.

(z)5q(N

or N

) for 0,z,d. Integrating (8.3) twice then gives

a quadratic dependence:

V(z)52q(N

or N

)(d2z)

/(2««

), (8.6)

for 0,z,d, with V(z)50 for z$d, which is known as the Schottky approximation, see

ﬁgures 8.4(b) and (c). A detailed discussion with examples is given by Lüth (1993/5,

chapter 7).

The key point is to realize how the screening length L and depletion length d depend

on the doping level in typical semiconductors. Inserting a set of values into (8.5), for

Si with

511.7 or Ge with

516, a low doping level n

510

(or equivalently 10

) gives L5410 nm for Si and 480 nm for Ge. However, for a typical surface poten-

tial V

50.8 V, the depletion length d is greater than 3 mm; since d.L the Schottky

model is most appropriate. These lengths are very long relative to atomic dimensions;

although they will decrease as (n

or p

) increase, they are much greater than 10 nm, at

least until samples are heavily doped, and have properties approaching those of metals.

Thus it is not surprising that models of the electrical behaviour of semiconductors are

typically not unduly concerned with atomic scale or surface properties. On the other

264 8 Surface processes in thin ﬁlm devices

hand, as devices get smaller, such eﬀects can be pervasive throughout the whole device,

and the unwanted statistical distribution of impurities may well pose a limit to device

dimensions in future.

8.1.3 Techniques for analyzing semiconductor interfaces

Classical experiments to determine the depth of the depletion layer and the barrier

heights include C–V proﬁling, where the same types of arguments as used above show

that C

is linearly proportional to the bias voltage V, with an intercept which gives

and the photo-electron yield or photocurrent, where the square root of the yield versus

photon energy gives a straight line with intercept

(Sze 1981, Schroder 1998). By

biasing the sample with a d.c. oﬀset, and using a.c. techniques for probing and detect-

ing, more subtle techniques including deep level transient spectroscopy (DLTS) have

been developed, and used to study the distribution of electrically active defects with

depth. An example related to point defects produced during InGaAs thin ﬁlm growth

is given by Irving & Palmer (1992); but it is noticeable that deductions about the nature

of the defects responsible are at best rather indirect.

Semiconductor devices are very demanding in terms of analytical techniques, since

one would like to know the density and depth distribution of the dopants, and of other

impurities (Schroder 1998). Of the wide range of surface analytical techniques avail-

able, so far only secondary ion mass spectrometry (SIMS) has been widely applied;

although it is destructive, it does have the necessary sensitivity, and it speciﬁcally iden-

tiﬁes the elements in question. The calculation in section 8.1.2 above can be used to

estimate the sensitivity needed: to detect 10

dopants in a depletion layer of

thickness 400 nm, over 1 mm

sample area means detecting and quantifying 4310

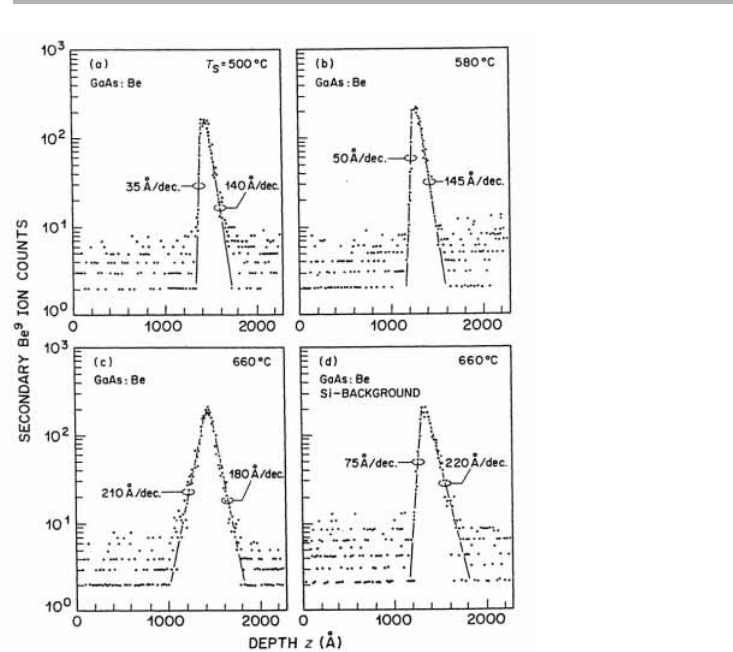
atoms. A determination of the depth distribution of (delta-doped) Be dopants in GaAs

by SIMS is shown in ﬁgure 8.5. Note that deductions about the eﬀects of annealing

temperature and ‘knock-on’ eﬀects during implantation have been made (reliably) from

proﬁles containing a maximum of only 200 counts/channel (Schubert 1994).

Although STM and related spectroscopies (STS) have revolutionized surface

imaging since the early 1980s, it is perhaps less clear whether similar advances in

8.1 Metals and oxides in contact with semiconductors 265

Figure 8.4. Depletion layer below an n-type semiconductor surface: (a) band bending showing

ionized donors above the Fermi level E

; (b) charge density

(z); and (c) potential variation

V(z) in the Schottky approximation.

(a)

(b)

(c)

Vz()

ρ()z

dLor

imaging buried interfaces, such as delta-doped layers, can be made. However, ex situ

TEM/HREM and diﬀraction are very powerful, and have been widely applied to semi-

conductor interfaces. There are several related techniques including Fresnel (out of

focus) imaging, which can image layers in proﬁle with ML precision (Shih & Stobbs

1991). Convergent beam electron diﬀraction (CBED, see ﬁgure 3.1(d)) and convergent

beam imaging (CBIM) are powerful means of measuring small strains and distortions

in multilayers (Humphreys et al. 1988). In situ studies of reactions in UHV are very

demanding research projects, which have been pursued by relatively few groups; but

semiconductor interfaces have been prime targets for the application of these tech-

niques (Yagi 1993, Ross et al. 1994, Gibson et al. 1997, Collazo-Davila et al. 1998,

Marks et al. 1998).

One new STM-based technique has enabled some relevant device oriented studies to

be performed on a microscopic scale, as described below. This variant, known as bal-

listic energy emission microscopy (BEEM) was invented in the late 1980s (Kaiser & Bell

1988, Bell & Kaiser 1988). Reviews of this rapidly developing area have been given by

Prietsch (1995), by Bell & Kaiser (1996) and von Känel et al. (1997). The schematic

266 8 Surface processes in thin ﬁlm devices

Figure 8.5. SIMS proﬁle of Be delta-doped GaAs grown by MBE at: (a) 500, (b) 580 and

(after Schubert 1994, reproduced with permission).