Venables J. Introduction to Surface and Thin Film Processes

Подождите немного. Документ загружается.

oﬀsets are often divided into three classes: type I, or straddling alignment, is as illus-

trated in ﬁgure 8.11(b) is appropriate for Ge/GaAs or GaAs/AlAs; type II, or staggered

alignment, is as shown in ﬁgure 8.11(a), which is observed in the InAs/AlSb system.

There is also a type III, or broken-gap alignment, observed for InAs/GaSb in which the

bands do not overlap at all

(Davies 1998, section 3.3). There are two types of problem,

one apparent, one real; let us get appearances out of the way ﬁrst. Figure 8.11 shows

schematically the energy positions E

and E

, but it does not show the dependence of

these energies on the k-vector, i.e. the detailed band structure, which is shown sim-

pliﬁed, in a rather unrealistically symmetric alignment, in ﬁgure 8.10.

Band structures are rather diﬀerent for the various bulk semiconductors, as can be

explored via the problems and projects given for chapter 7. When calculating energies

such as E

, a detailed integration is done for both the valence and conductions bands

over the entire 3D Brillouin zone. In the integration, the

-point (k50) contributes

negligibly; high densities of states are typically concentrated at the zone boundaries

and near various maxima and minima, such as the valleys associated with indirect gaps.

The calculation reﬂects the ‘center of gravity’ of the two bands. Zone boundary states

correspond to standing waves, and in a bulk compound semiconductor such states may

be preferentially located over one type of atom. The shift in E

is associated with

(partial) electron transfer from cations to anions which diﬀers across the interface, also

associated with diﬀerent band structures (curvatures) in the two materials.

8.2 Semiconductor heterojunctions and devices 277

Table 8.1. Some calculated valence band oﬀsets across low misﬁt (001) interfaces in

comparison with experimental DE

values

Unstrained misﬁt Band gaps at Calculations Experiment

Interface at 300 K (%)

300 K (eV)

(eV) DE

(eV)

Ge/GaAs 10.09 0.66/1.42 20.63

, 0.32

20.53

20.58–0.62

20.5160.09

GaAs/AlAs 20.12 1.42/2.15 20.37

, 0.55

20.50

20.5860.06

20.5060.05

InAs/AlSb 21.27 0.35/1.62 20.05

20.13

20.1760.1

20.1860.05

InAs/GaSb 20.62 0.35/0.75 20.38

,–0.40

20.51

20.5460.02

20.5560.05

References: (a) Van de Walle & Martin 1986; (b) Tersoﬀ 1987; (c) range of values from Yu et

al. 1992, mostly excluding measurements without error bars; (d) Montanari et al. 1996; (e)

Peressi et al. 1998, (e*) for the two-layer mixed interfaces discussed in the text; (f) Davies 1998,

Appendix 2, (f*) section 3.3.

Note that the language here can be confusing: Yu et al. (1992) have two subsets of type II to cover these

two materials, and a diﬀerent type III; there is also a sign convention which is unevenly applied. Here we

use a negative sign for DE

if the valence band edge of the narrower gap material is lower in energy than

that of the wider gap material. This has the advantage of not having to remember which type is involved

when interpreting DE

and Q

. There does not seem to be an accepted standard convention.

So what real problems remain? Although the MIGS and related models are relatively

satisfying, professionals in this ﬁeld clearly do not believe that they contain the whole

story, and can demonstrate that interface chemistry/ segregation plays an important

role in addition (Brillson 1994, Mönch 1994). They can then consider tailoring the

interfacial layers to produce particular desired oﬀsets (Franciosi & Van de Walle 1996).

For example, we can show that the composition of the interface layer does play a role.

As argued by Peressi et al. (1998), the Tersoﬀ model for the diﬀerences in DE

between

diﬀerent heterostructures with the same substrate, or between diﬀerent Schottky

barrier heights D

with the same metal as shown in ﬁgure 8.12, indicates that these

diﬀerences are largely due to bulk properties. On the other hand, the absolute values

are not merely bulk quantities, and the models discussed so far only work for non-polar

interfaces, or for polar interfaces between homovalent materials, such as Ge/Si(001),

which is of course strongly strained. The supposedly simple Ge/GaAs (001) junction

would have two extreme ways of forming a sharp interface, i.e. termination with Ga or

As, but as such an interface would be charged it must either reconstruct and/or inter-

278 8 Surface processes in thin ﬁlm devices

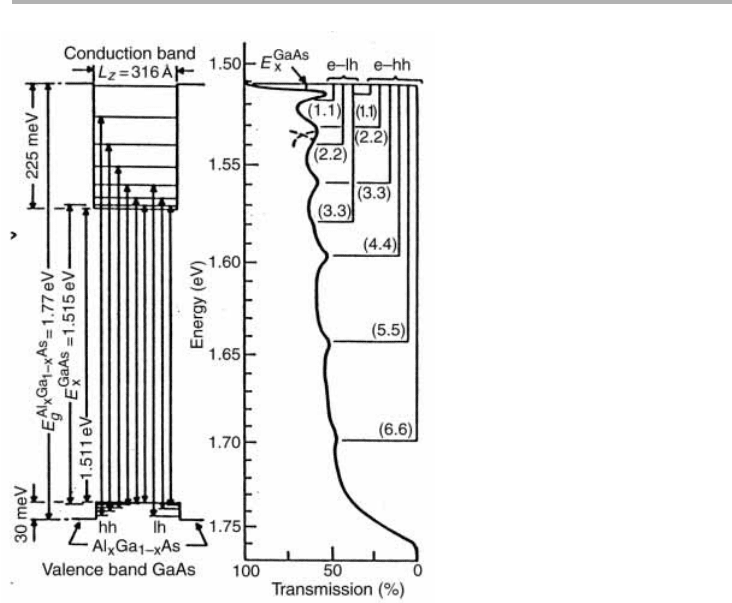
Figure 8.15. Eﬀective mass analysis of a particular GaAs quantum well, surrounded by

12x

As with x50.21. The left hand panel shows the predicted heavy and light hole

transitions and band oﬀsets, and the well thickness, all of which were deduced from the

absorption spectrum shown in the right hand panel (from Duggan 1987, reproduced with

permission).

mix. There are two possibilities for an isolated neutral mixed plane, (AsGe)

1/2

(GaGe)

1/2

, which were calculated to have valence band oﬀsets diﬀering by 0.6 eV; this

diﬀerence is much greater than the uncertainty in experimental values, but the average

is closely the same as for the non-polar (110) interface.

The real material has many possible ways to intermix and thereby minimize charge

imbalance across the interface, and a better option was thought to be mixing over two

planes, so that the interface dipole could be reduced to zero. Again there are two

options involving (Ga

Ge)

1/4

followed by (GaGe

)

1/4

, or vice versa. Now the calcula-

tions shown in table 8.1 give 0.62 and 0.58 eV, much closer to each other and to experi-

ment (Biasiol et al. 1992). To ﬁnd the actual structure and the VBO at the same time is

a challenge, since there are several structures worthy of attention which have similar

energies. Nonetheles, Peressi et al. (1998) conclude that MIGS-related (or better

termed, linear response theory) models form a very good starting point, provided one

discusses the interface that is actually present. For the ‘model solid’ approach (Van de

Walle 1989), the eﬀects of strain can be incorporated in a natural way without further

approximation; this method is therefore favored for calculations on strained layer inter-

faces.

The examples where these models clearly don’t work correlate with strong chemi-

cal/metallurgical reactions and/or steps or other defects at the interface, with asso-

ciated trapped charges and/or dipoles. One could counter by saying that in these cases,

the interface is simply not what was initially postulated. If one adds the evidence now

being obtained from BEEM about large lateral variations in barrier heights, and in

transmission coeﬃcients across such interfaces, then variability is not surprising.

Technology in one sense is all about processing: in that context variability which one

cannot control is the real disaster. But in making the transition to scientiﬁcally based

industry, understanding is also very important. Without it, any small change in pro-

cessing conditions forces a return to trial and error, with typically a huge parameter

space to explore – preferably by yesterday, or you are out of business!

8.2.4 Modulation and

-doping, strained layers, quantum wires and dots

In heterostructures, we also have to have provide carriers via doping. But if the layers

are narrow enough, we may be able to put the dopants at diﬀerent positions and

thereby increase carrier mobilities by strongly reducing charged impurity scattering.

This is one of the key points behind modulation doping, and is a factor in

-doping,

i.e. doping on a sub-ML scale, which can be used to change the shape of quantum wells

(Schubert 1994). A limit to such techniques is the fact that dipoles are set up between

the layers, which will also bend the bands. Depending on the doping level, the various

length scales may or may not be comparable, and the models used will be diﬀerent in

detail. Understanding the eﬀect of diﬀerent length scales in models of condensed

matter has a long history (Anderson 1972, Kelly 1995 chapter 3) and the topic contin-

ues to attract comment (Jensen 1998). Transitions in dimensionality, from 3D to 2D

and so on down to 0D, are also of interest in the same sense. For example, a layered

8.2 Semiconductor heterojunctions and devices 279

heterostructure which behaves as a 2DEG in zero magnetic ﬁeld, becomes a 0DEG dot-

like structure in a strong magnetic ﬁeld, as the size of the cyclotron orbit becomes less

than the lateral device dimensions. This is a key aspect of various devices based on

‘quantum conduction’: often the leading edge devices only work at low temperatures

and/or in a high B ﬁeld. Such devices are competitive in applications where ultimate

sensitivity is required (e.g. telephone/TV satellite transmission and reception, or in

astronomy), but not in domestic receivers whose emphasis is on optimum room tem-

perature performance, where high electron mobility transistors (HEMTs) based on

GaAs/(AlGa)As are a success story (Kelly 1995 chapter 5).

Some of these dimensional transitions are exempliﬁed in strained layers, of which

the archetype consists of GeSi alloys of various compositions on Si(100). The com-

pressive strain due to 4.2% larger lattice constant of Ge means that the layers have a

tetragonal distortion, which lifts the degeneracy of the four valence band minima with

k parallel to the layer from the two with k perpendicular to the layer. This, and the

switch of the position of the conduction band minimum at high Ge composition, inﬂu-

ences both the band gap and oﬀsets as a function of both composition and strain (see

e.g. Kelly 1995 chapter 14, or Davies 1998 chapter 3). A realistic feel for the amount of

work done on this one system may be obtained from the reprint collection made by

Stoneham & Jain (1995), and the other references cited in section 7.3.3.

Quantum wires can be formed on a linear surface structures, the most obvious of

which are vicinal surfaces consisting of arrays of steps. Experiments on a variety of

conﬁgurations based on GaAs and AlGaAs are described by Petroﬀ (1994). The

problem is that individual steps are typically too rough to make this approach work,

unless regular multi-atomic height steps can be reliably fabricated; this is a current

research eﬀort. It is not yet clear that such approaches can supplant lithography tech-

niques (Prokes & Wang 1999). Similarly, quantum dots, in Ge/Si for example, need to

be rather uniform in size to be useful; the question of whether one can persaude them

to do this during growth of their own accord (i.e. via self-organization), or whether one

uses lithographically patterned substrates is also a hot topic, which is discussed further

in section 8.4. A discussion of early results using patterned layers is given by Kapon

(1994); these eﬀorts overlap with the topics discussed here in sections 5.3 and 7.3.

8.3 Conduction processes in thin ﬁlm devices

The conductivity and the resistivity

are among the simplest material parameters to

measure, one only needs a voltmeter and an ammeter. They are also some of the most

useful properties, especially when they are non-linear and can thereby be used to

amplify or store currents or voltages, as in essentially all active electronic devices. Yet

it is an irony that what is easiest to measure and experience can also be the hardest to

set on a ﬁrm scientiﬁc foundation, or to describe quantitatively with few unknown

parameters. Here we explore in the simplest terms why this is the case, and indicate the

role that surface and interface processes play in electrical and magnetic properties of

thin ﬁlms.

280 8 Surface processes in thin ﬁlm devices

8.3.1 Conductivity, resistivity and the relaxation time

All electrical properties of thin ﬁlm devices depend essentially on the number of charge

carriers and the scattering processes to which these charges are subjected. To study

such topics we need access to a book describing conduction processes in the relevant

type of material. For normal metals and alloys, Rossiter (1987) is excellent; however,

this book does not discuss superconductors or semiconductors even in outline. The

reason is simply that these three topics are enormous ﬁelds, each with its own appro-

priate starting point. For superconductors, much eﬀort has to be expended to describe

the thermodynamic and quantum mechanical nature of the superconducting state,

before one can consider the eﬀects of bulk scattering and then thin ﬁlm and surface

eﬀects (Tinkham 1996). The fabrication of useful high-T

ceramic wires and tapes is a

major technical challenge.

In particular, we can note that in semiconductors, most attention is paid to the

number and type of carriers, and then we consider scattering processes which deter-

mine carrier mobility. For example, we write the conductivity

5q(n

or p

), (8.10a)

in terms of the electron or hole mobilities

and

, given by

/m*, (8.10b)

where both the densities, n or p, and the scattering processes which lead to the eﬀective

scattering time

, are determined by the defect density. Note that the word or is used

here in the same sense as in section 8.1.2, to avoid too detailed a discussion of what

happens if both n- and p-type dopants are present simultaneously, when extra care is

always required. The eﬀective mass is inversely proportional to the band curvature, and

is in general a tensor quantity.

In metals, the number of carriers is essentially ﬁxed, and the spotlight is on scatter-

ing processes. Elementary considerations start with the Drude model, and show that

the conductivity is proportional to the density n of conduction electrons and the relax-

ation, or scattering, time

between collisions as in equations (8.10) and (8.11). Moving

to the quantum model with the correct Fermi–Dirac distribution function f

, we realize

that only those electrons n(k) close to the Fermi energy participate in the scattering,

and that the scattering time is now quite a complex average of all scattering processes.

In the regime where the linearized Boltzmann transport equation (Rossiter 1987,

chapter 1) is appropriate and we consider only elastic scattering,

5(2p)

兰

dk9Q

kk9

(12 f

), (8.11)

where Q

kk9

is the matrix element for scattering processes from k to k9 which conserve

energy.

In general, the conductivity, relating the current density J to the electric ﬁeld E is a

second rank tensor J

and the conductivity can be expressed as an integral over

the Fermi surface S as

5{e

/(2p

h)}

兰

(k)v

(k)dS/ |v(k)|, (8.12a)

8.3 Conduction processes in thin ﬁlm devices 281

where v(k) is the Fermi velocity. For a cubic or amorphous metal, where the relaxation

time is a function of the magnitude of k, but not of direction, (8.12a) simpliﬁes to

5{e

/(6p

h)}

兰

v(k)dS, (8.12b)

so that

and

are both scalar quantities and

. But, even so, we note that if a

new scattering mechanism is added in (8.12), this will contribute to

, where the

shortest time will dominate, but that the contribution to

(in (8.12) as in (8.10)) is pro-

portional to

. Thus the contribution of a new scattering process to the resistivity

as an inverse of an inverse.

8.3.2 Scattering at surfaces and interfaces in nanostructures

Given that many materials in general, and surface scattering in particular, are not

intrinsically isotropic, the contribution of surface or 2D interface processes to the resis-

tivity can be quite complicated. The ﬁrst model applicable to thin ﬁlms, which assumed

an isotropic Fermi surface, was summarized by Sondheimer (1952) in terms of a single

parameter p which characterized whether the scattering at the surface was specular (p

51) versus diﬀuse (p50). Diﬀerent formulae are applicable to wires or grain boundar-

ies (Sambles & Preist 1982, Rossiter 1987 chapter 5), but for the thin ﬁlm case, the

Fuchs–Sondheimer formula is

512 (t

) (8.13)

where

is d/

, and t is the integration variable corresponding to the direction of elec-

tron travel. This formula clearly shows that as p →1 there is no extra scattering due to

the surface, but if the scattering has a diﬀuse component, then the resistivity ratio

rises rapidly as the ﬁlm thickness d becomes less than the scattering mean free path

in the corresponding bulk material, i.e. as

→0. This formula is not the most accurate,

but it is the simplest which has analytic limits.

The earliest comparisons with experiment typically showed agreement with (8.13)

with p close to zero, the diﬀuse scattering limit. However, these early experiments were

largely limited to thin polycrystalline ﬁlms in which grain-boundary scattering played

a crucial role. In several experiments, Al ﬁlms were used which has a rough oxide on

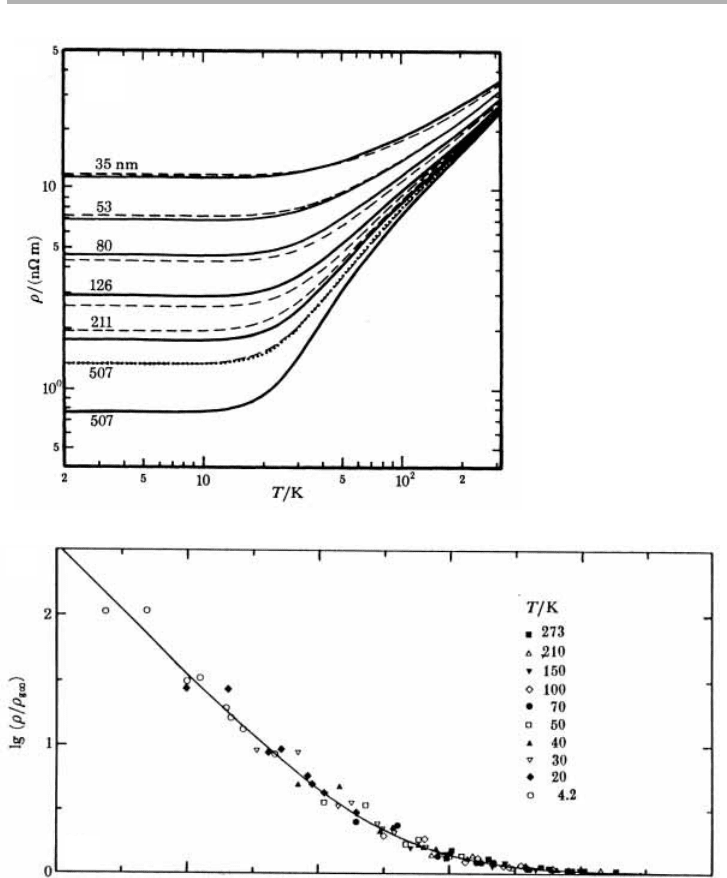
the surface. A particularly careful study of the resistivity of Au ﬁlms grown on mica

and KBr was made by Sambles et al. (1982), as illustrated in ﬁgure 8.16. Here Au(111)

samples of diﬀerent thicknesses were grown on mica, and the resistivity measured as a

function of temperature. We can see in ﬁgure 8.16(a) that at low temperatures there is

a substantial residual resistivity which increases with decreasing ﬁlm thickness. The

same data plotted on a logarithmic scale of

versus

shown in ﬁgure 8.16(b) gives

a good ﬁt to the more detailed model of Soﬀer (1967), but the ﬁt may not be uniquely

due to surface scattering. Internal surfaces such as grain boundaries can mimic surface

scattering if the grain size is larger in thicker ﬁlms (Sambles 1983). He concluded that

‘p’ in such ﬁlms can be as high as 0.65, and that grain and twin boundary scattering

冢

1 2 exp( 2

1 2 p exp( 2

冣

冥

冤

3(1 2

)

冕

282 8 Surface processes in thin ﬁlm devices

can also be strong. Thus from here on we consider both internal interfaces and exter-

nal surfaces as sources of scattering.

Electron transport in semiconductor structures with dimensions down to a few

nanometers have many interesting (and sometimes disturbing) properties for future

devices. There is a limit due to the statistical distribution of donors, acceptors and scat-

tering centers. A simple calculation shows that a device based on 10

donors or

8.3 Conduction processes in thin ﬁlm devices 283

Figure 8.16. (a) Temperature dependence of the resistivity of Au(111) ﬁlms of diﬀerent

thicknesses grown on mica, showing strongly thickness dependent residual resistivity; (b) the

same data on a log–log plot of

versus

5d/

(after Sambles et al. 1982, reproduced with

permission).

(a)

(b)

acceptors, a relatively high doping level, will have only one impurity somewhere in the

width of a 10 nm square wire. Chaotic eﬀects are expected once the number of elec-

trons/ impurities drop to below ⬃10 per device cross section, so the size region ,30 nm

is considered very dubious. We are not there yet: the next generation of 0.13 mm

(130 nm) linewidth devices is in the pipeline, but it is not too soon to start worrying

about these topics.

Second, the size eﬀect on electronic energy levels, as illustrated in ﬁgure 8.14 for

quantum well structures, means that via electron–electron interactions, energy levels in

the device depend on the occupation numbers of the diﬀerent electron energy levels.

This is of course the same as in individual atoms and molecules, but in the case of

.10 nm sized devices, the energy levels are much closer together. Thus at suitably low

temperatures, conduction processes through these devices will be aﬀected by the eﬀects

known collectively as the Coulomb blockade. This is a rich ﬁeld for theoretical research

and experiments at low temperature and high magnetic ﬁelds (Ferry & Goodnick

1997), and is the origin of collective aspects of electronic behavior behind the frac-

tional quantum Hall eﬀect and the 1998 Nobel prize for Physics awarded to Luttinger,

Störmer and Tsui (Mellor & Benedict 1998, Schwarzschild 1998).

But before we all get carried away, we should note that the reason these subtleties

can be observed at all is due to the low temperature and high magnetic ﬁelds which

allow the closely spaced energy levels to be separated. As Störmer himself noted on the

award of the prize ‘No, it won’t revolutionize telecommunications’ (Schwarzschild

1998). Devices which operate at room temperature (or even 77 K) need to be more

robust in this sense. But many groups are involved in the race to demonstrate single

electron transistors (SETs) which work at room temperature. The active regions of such

devices must have a characteristic dimension ,10 nm (Devoret & Glattli 1998). This

is the principal reason for believing that if even smaller devices are to become impor-

tant in future, then the carrier density needs to be higher than in typical semiconduc-

tors. For example, such devices are increasingly sensitive to random radiation eﬀects as

the number of carriers is reduced. Interest is therefore turning to metallic systems, and

in particular to magnetic eﬀects which can be used in non-volatile devices; some of

these are described in the next section.

8.3.3 Spin dependent scattering and magnetic multilayer devices

The giant magneto-resistance (GMR) eﬀect is the reduction of (longitudinal) resis-

tance in the presence of a (parallel) magnetic ﬁeld, typically in a magnetic multilayer.

In a large ﬁeld, where the magnetization in all the layers are lined up, the ‘spin-ﬂip’ scat-

tering of the conduction electrons is minimized, whereas when some of the layers are

aligned antiparallel it is greater. The biggest eﬀects observed are changes of up to 80%

of the resistance at high ﬁelds at low temperatures. Note that the sign of the magnetor-

esistance in ferromagnetic materials, decreasing as the ﬁeld is increased, is opposite to

that in normal metals, where the helical paths followed by electrons in an external ﬁeld

yield more opportunities for scattering. This distinction is spelled out in an inﬂuential

report (Falicov et al. 1990), which was largely responsible for setting the agenda for

284 8 Surface processes in thin ﬁlm devices

research on magnetic materials and thin ﬁlm devices during the 1990s. The push is now

on to integrate magnetic superlattices with semiconductors, with the goal of high

density non-volatile memory a realistic prospect in the not too distant future (DeBoeck

& Borghs 1999, Daughton et al. 1999).

In magnetic materials we have to consider that there are two resistivity channels

↑

and

↓. At low temperatures in ferromagnetic materials, spin-ﬂip scattering is frozen

out, meaning that the spin-up and spin-down channels behave independently and that

conductivities add as

↑1

↓, or equivalently

↑)

↓)

. Within each

resistivity channel, we have the diﬀerent scattering mechanisms contributing in propor-

tion to inverse relaxation times as discussed in section 8.3.1, and at ﬁnite temperatures

magnon scattering, which tends to equalize the contributions of the two spin channels,

is also possible. Thus it is not surprising that this topic can get quite complicated quite

quickly; a useful introduction in the context of magnetic multilayer devices, where spin

dependent scattering at interfaces is the most important eﬀect, is given by Fert & Bruno

(1994). Spin dependent scattering of the same type has also been demonstrated at

aligned domain walls in pure Co and Ni ﬁlms (Gregg et al. 1996).

Multilayer devices can be constructed in various diﬀerent geometries, limiting cases

being when the current is either in the plane (CIP) or perpendicular to the plane (CPP).

The way in which one of the two resistivity channels can short circuit the other depends

on the device geometry. For a sizable device, the CIP geometry tends to have the higher

resistance, but the boundaries between the layers are less eﬀective in producing spin

ﬂips than in the CPP geometry, which has higher resistivity. But the low resistance of

the conventional CPP geometry means that the eﬀects due to the thin device are very

diﬃcult to measure, because all the other resistances add in series. This CPP problem

has lead some workers to go to considerable lengths to create structures in the CAP

geometry, with the current at an angle to the plane, which can be done by using ridged

substrates at an angle

, is illustrated in ﬁgure 8.17(a).

The conductivity in the CAP geometry combines those of the other geometries as

CAP

CIP

cos

CPP

sin

, (8.14)

and there are similar formulae for the combination magneto-resistance (Levy et al.

1995). Ono & Shinjo (1995) and Ono et al. (1997) have used Si(001) wafers, and have

etched V-grooves with {111} facets into this substrate, on which the multilayers are

grown. By varying the angle of the current direction

, they could measure

CAP

and

CIP

on the same samples, and use interpolation formulae to estimate

CPP

. The results

of a particular sample are shown in ﬁgure 8.17(b); this corresponds to a 4 mm thick,

91-layer stack of four individual layers with composition Co(1.2)/Cu(11.6)/NiFe(1.2)/

Cu(11.6), where the layer thickness in nm is given in brackets. Note that the MR ratio

for this system in the CAP geometry reaches almost 50% at low temperature and is

around 10% at room temperature. Although one could use higher values, these are

8.3 Conduction processes in thin ﬁlm devices 285

This notation allows one to write an article entitled The art of sp↑n electron↓cs (Gregg et al. 1997), but the

large number of authors on this paper suggests that they know they could only do this once and get away

with it.

286 8 Surface processes in thin ﬁlm devices

Figure 8.17. (a) Schematic illustration of a multilayer constructed on a substrate containing

V-grooves at characteristic angle

, with the current ﬂowing in a direction given by the angle

;

(b) the measured magneto-resistance observed as a function of temperature in the CIP and

CAP geometries, and the estimated CPP results, for a composite multilayer of Co/Cu/NiFe/Cu

as described in the text (from Shinjo & Ono 1996, reproduced with permission).

(a)

(b)