Venables J. Introduction to Surface and Thin Film Processes

Подождите немного. Документ загружается.

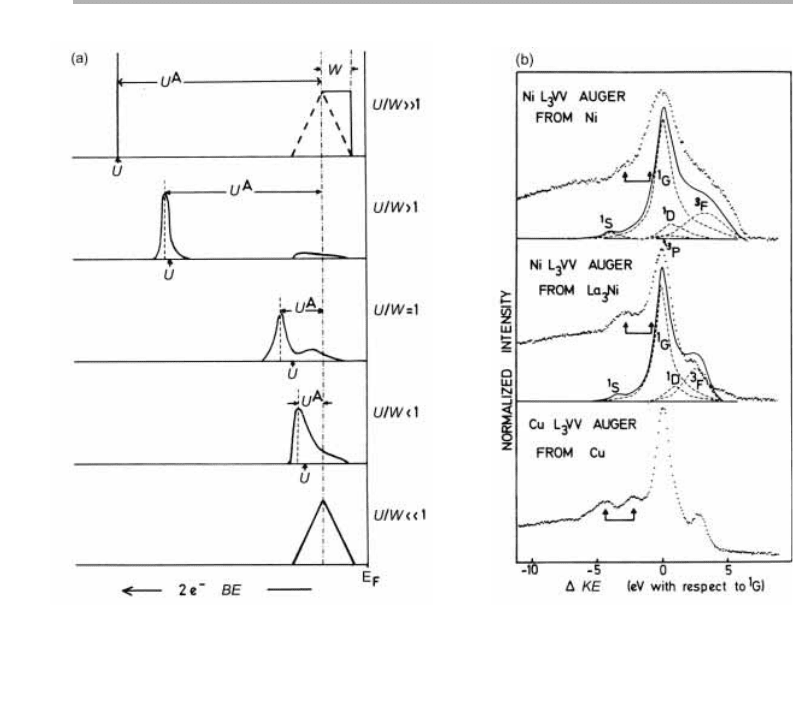
atom (the correlation energy U, often associated with the ‘Hubbard’ model), versus the

valence band width, W (Verdozzi & Cini 1995). If U/W is ,,1, we see an unshifted self

convolution (self fold) of the valence band, corresponding to a delocalized, band-like

ﬁnal state; in the other limit (W/U ,,1) we see a shifted, but atomic-like, line. The

Auger CVV transitions then show multiplet structure where the details depend on the

variation of the matrix elements with the orbital character of the ﬁnal state.

As a result of these considerations the lineshape can switch from one type to the

other across a series of alloys. This eﬀect happens particularly for nearly ﬁlled d-shells,

as in Pd or Ni alloys and silicides. A schematic diagram of this eﬀect plus an example

of Ni LVV in Ni-based alloys (Fuggle et al. 1982, Bennett et al. 1983) is shown in ﬁgure

3.16, but there is ongoing discussion about how such models apply to unﬁlled bands,

where many diﬀerent possibilities for screening exist. This type of work is reviewed by

Weightman (1982, 1995) and Hüfner (1996), and is becoming more important as the

ﬁner aspects of electron spectroscopy, including spin-polarized electron spectroscopy

of magnetic materials as discussed in chapter 6, can be interpreted in terms of the elec-

tronic structure.

All these electron spectroscopies derive their surface sensitivity from the low inelas-

tic mean free path (imfp) of electrons, which has a minimum in the neighborhood of

3.3 Inelastic scattering techniques 87

Figure 3.16. (a) Calculated Auger emission spectrum as a function of U/W for a CVV Ni

spectra; (b) comparison of Ni L

VV in Ni and in La

Ni with Cu L

VV Auger spectra,

including calculated (full and dashed) lines based on appropriate values of U for the diﬀerent

atomic states (after Bennett et al. 1983, reproduced with permission).

50–100 eV, and a typical minimum value of around 0.5 nm. Calculating the imfp has

become a major activity in its own right (Powell 1994, Powell et al. 1994), but it is only

in special cases that it can be readily obtained experimentally. One case which is soluble

is when a deposit grows in the layer by layer mode. We consider this in connection with

AES quantiﬁcation in the next section; other techniques are not considered here, but

the approaches and problems are all very similar.

The general form of

(E) has been given as

(in ML)5538/E

10.41 (aE)

1/2

, where

a is the ML thickness in nm (Seah & Dench 1979). This formula, widely used in the

1980s for want of a better alternative, shows a minimum at about 50eV, but the form

used is not rigorous; if you are doing detailed work you will need a more accurate

expression, such as that given by Tanuma et al. (1991, 1993). The underlying physics is

that at high E, we have the Bethe loss law for inelastic electron scattering, which shows

that (2dE/dx)⬃E

ln(E/I), with I equal to the mean ionization energy ⬃10–15 eV.

(E) increases as E/ln(E/I), approximated by E

1/2

in the Seah & Dench formula, since

is ⬃(dE/dx)

. At lower energy

(E) goes up strongly as E decreases, because of the

lack of states into which the electron can be scattered. For example, if the main scat-

tering mechanism is creation of plasmons with an energy of ⬃15 eV, then if the energy

is within 15 eV of the Fermi level, the scattering cannot occur because the ﬁnal state is

already occupied. This then becomes a phase space limitation at low E, which has an

dependence.

3.4 Quantiﬁcation of Auger spectra

3.4.1 General equation describing quantiﬁcation

The general equation governing the Auger electron current, I

caused by a probe

current I

can be written down straightforwardly, but is not immediately transparent,

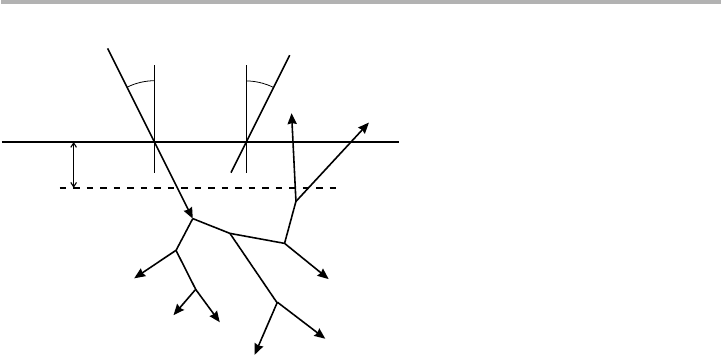
and really needs to be explained using a schematic drawing, such as ﬁgure 3.17. The

incoming electron causes an electron cascade below the surface, whose spatial extent is

typically much greater than the imfp. For example, the spatial extent is about 0.5 mm

at an incident energy E

520 keV, but also depends on the material and the angle of

incidence,

. As a result Auger electrons can be produced by the incoming primary

electron beam, and also by the backscattered electrons as they emerge from the sample;

the Auger signal intensity thus contains the backscattering factor, R, which is a func-

tion of the sample material, E

and

The ratio I

can be expressed as a product of terms describing the production and

detection of the Auger electrons, as ﬁrst developed by Bishop & Rivière (1969). The

Auger yield Y is the number of Auger electrons emitted into the total solid angle

(

5 4p sterad). It is therefore not dependent on the details of the analyzer. The detec-

tion eﬃciency D of the analyzer can be written as (T·«), where T is a function f(

/4p),

being the solid angle collected by the analyzer, and « is f(DE/E), most simply

«5(DE/E). Thus

88 3 Electron-based techniques

5Y·D5[

R]·sec

·N

(T·«). (3.8)

Here we have Y expressed as the cross section for the initial ionization event (

), the

Auger eﬃciency (

), discussed in outline in section 3.3, and the factor R. The sec

term

describes the extra ionization path length caused by having the primary beam at an

angle to the sample normal. Finally N

is the eﬀective number of atoms/unit area con-

tributing to the (particular) Auger process.

What we actually want to know is: given a measured signal I

, how many A-atoms

are there on the surface? Typically there is not a unique answer to such a simple ques-

tion, because the signal depends not only on the number of atoms but also on their dis-

tribution in depth. There are two cases which can be solved uniquely, which are

instructive in showing how such analyses work. The ﬁrst is when all the atoms are in

the surface layer: then N

, and if one knew all the other terms in the equation, we

could determine N

The second case is when the atoms are uniformly distributed in depth: in this case

we can show that N

, where N

is the bulk (3D) density of A-atoms. The proof

of the second case is as follows. We work out

·T)5(1/4p)

兰兰兰

N(z) exp(2z/

cos

)·sin

dz, (3.9)

where the integral is over the two analyzer angles (

) and depth z. The path length

in the sample in the direction of the analyzer is z/cos

, so we are assuming exponen-

tial attenuation without change of direction; this is reasonable for inelastic scattering

of the outgoing electrons. Because N(z)5N

is constant, we can do the integration

over z ﬁrst. This gives

3.4 Quantiﬁcation of Auger spectra 89

Figure 3.17. Schematic diagram of electron scattering in a solid, indicating the incident and

detected angles,

and

, plus the role of backscattered electrons in determining the Auger

signal strength. The escape depth is qualitatively the thickness of the region from which most

of the detected Auger electrons originate, of the same order as the imfp discussed in the text.

Auger electron

Backscattered

electrons

Auger

escape

depth

Primary

electron

beam

Electron

cascade

·T)5

·(1/4p)

兰兰

cos

·sin

·f(

). (3.10)

The angular double integral is just the cosine electron emission distribution, integrated

over the solid angle of the analyzer; so f5T, N

, as required.

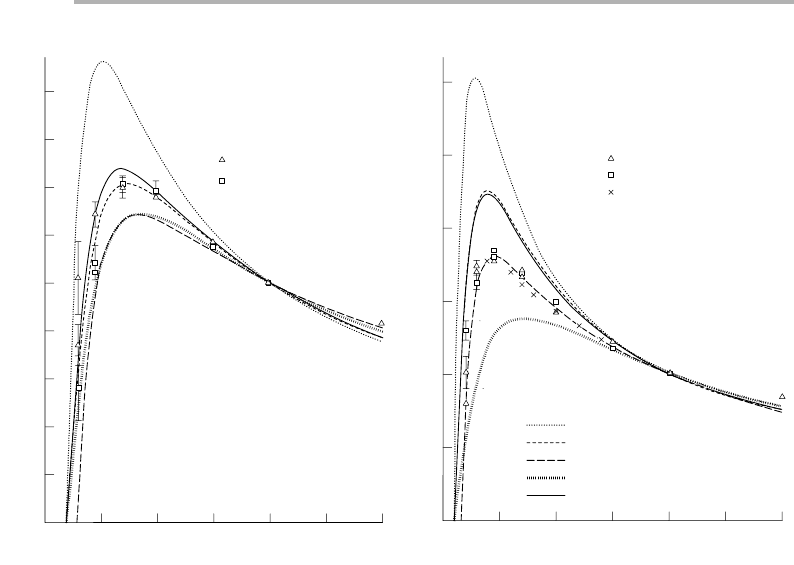
A detailed experimental and computational study of the Auger signals from bulk

elements has been performed, amongst others, by Batchelor et al. (1988, 1989). These

studies show that the dependence of the Auger peak height on primary beam energy

explores the variation of (

R) as shown in ﬁgure 3.18 for Si KLL and Cu L

MM;

the variation with

is determined by (Rsec

·T). The dependence on atomic number

Z is complicated, since all the above material variables and the Auger energy are prop-

erties of the individual element in question.

To make these comparisons we took a particular ionization cross section, and cal-

culated the Auger backscattering factor R511r with this cross section, where r is

deﬁned as

r5(1/

) sec

)

兰兰

(E)(d

/dEd

)sin

dE, (3.11)

where the normal electron backscattering factor

is given by

兰兰

/dEd

)sin

dE. (3.12)

90 3 Electron-based techniques

Figure 3.18. Auger peak heights for (a) Si KLL and (b) Cu L

MM as a function of primary

energy E

, normalized to 20 keV, measured on Auger microprobe instruments at Harwell and

Sussex, compared to the product (

R) calculated with the cross sections indicated (after

Batchelor et al. 1989, reproduced withpermission).

1.8

1.6

1.4

1.2

1.0

0.8

0.6

0.4

0.2

0.0

3.0

2.5

2.0

1.5

1.0

0.5

0.0

10 15 20 25 30

(a)

Silicon 1610 eV θ

= 65°

0 5 10 15 20 25 30

Primary beam energy

(keV)Primary beam energy

(keV)

Normalised signal (20 keV)

Signal normalised to 20 ekV

Harwell MA500

Sussex HB50

Copper 914 eV θ

= 65°

Harwell MA500

Sussex HB50

Ichimuras results

Calculations

Worthington–Tomlin

Powell

Gryzinski

Lotz

Hartree–Fock

(θ

= 45°)

(b)

This means that the Auger backscattering factor can be written as R511

, where

the factor

is typically greater than 1, and depends on the energy and angular distri-

bution of backscattered electrons, and the Auger energy in relation to the beam energy.

Comparison of the energy dependences of the cross sections and other checks on abso-

lute values has advanced knowledge of which cross sections are reliable (Batchelor et

al. 1988, Seah & Gilmore 1996).

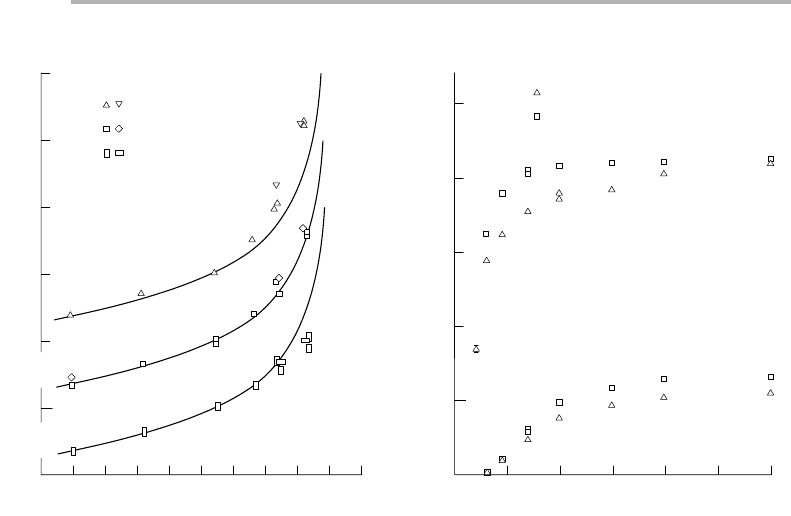
The peak to background ratio (P/B or PBR) can be measured accurately and is very

useful as an approximate compensation for topographic eﬀects. The angular depen-

dence is rather ﬂat as shown in ﬁgure 3.19(a) for Cu, Si and W Auger electrons meas-

ured in two diﬀerent instruments. The lines are a simple model calculation based on

P/B ~ sec(

)R(

(

), (3.13)

and it is seen that this model, normalized at normal incidence, gives a good ﬁt out to

at least

570°. At high incidence angle, there is much less variation in the back scat-

tering factor as a function of atomic number, and the background becomes dominated

by secondary electrons, which have similar excitation mechanisms to Auger electrons.

This is mirrored in the PBR as a function of E

, shown in ﬁgure 3.19(b). Above 15–20

keV both Cu L

MM and Si KLL show no dependence on E

; this eﬀect sets in at lower

for lower energy transitions, where the background comprises secondary rather than

backscattered electrons (Batchelor et al. 1989).

3.4 Quantiﬁcation of Auger spectra 91

Figure 3.19. Variation of Auger peak to background ratio for (a) Si, Cu and W with incidence

angle

, compared with model calculation based on (3.13); (b) Si and Cu with primary beam

energy E

at two incidence angles

565 and 75° (after Batchelor et al. 1989, reproduced with

permission).

4.0

3.0

2.0

1.0

0.0

–10 0 10 20 30 40 50 60 70 80 90

Tilt angle (deg)

Harwell MA500

Silicon

Copper

Tungsten

(a)

2.5

2.0

1.5

1.0

0.5

0.0

(b)

0 5 10 15 20 25 30

Primary beam energy

(kV)

Harwell MA500

Incident angle, θ

65°

75°

Tungsten 1730 eV

Silver 345 eV

Peak to background ratio

Signal normalized to 45

3.4.2 Ratio techniques

Detailed study of the basic quantiﬁcation equation leads to some interesting physics,

and often to a determination of one or more parameters of the experiment, but it does

not lead directly to easy sample analysis. For this we have to keep many of the experi-

mental parameters ﬁxed, and use standard samples for comparison. Ratio techniques

are common in all forms of quantitative analysis, principally because they allow one

to eliminate instrumental variables. The measurement is then the value of (I

) for

the sample (s), ratioed to the same quantity for the (pure element) standard (el).

Comparing the terms in the quantiﬁcation equation, we can see that the only terms

which do not cancel out, for bulk, uniformly distributed samples, are

)

/(I

)

5(R

)·(N

); (3.14)

the last bracket is what we want to know, and the previous term is a ‘matrix dependent’

factor. Without detailed calculation it is not obvious how such terms behave, but they

can sometimes vary slowly. For example, it has been shown that the matrix dependent

factors often vary linearly with composition in binary alloy systems (Holloway 1977,

1980). If one is stuck, one can establish standards closer to the composition of inter-

est. This might be seen as a last resort: it is clear that the smaller extrapolation one

makes, the more accurate the result is likely to be.

Many authors have developed programs for studying such eﬀects, and national stan-

dards organizations (National Institute for Standards and Technology (NIST),

National Physical Laboratory (NPL), etc.) are involved on an ongoing basis. The

author most concerned in the USA is C.J. Powell of NIST, who has written extensively

on this topic; his UK counterpart is M.P. Seah, who works for NPL; he has published

an interesting commentary on the needs of, and competing pressures in this ﬁeld (Seah

1996), and they have written several updates on the whole ﬁeld (e.g. Powell & Seah

1990). It is no accident that they have concerned themselves with these aspects of quan-

titative analysis, and indeed run conferences with the title Quantitative Surface Analysis

(QSA) at which such matters are discussed in great detail (Powell 1994); QSA-10 was

held in 1998. Round-robins, which use standard samples to be tested in the diﬀerent

laboratories, are one of the methods used to ﬁnd out where there is common ground

and where there are diﬃculties. By characterizing the analyzers carefully, the spectra

can be calibrated on an absolute scale, such as the example given earlier for Ge in ﬁgure

3.13 (Seah & Gilmore 1996).

There are also major consulting businesses based on such analyses, since the services

and expertise are often very expensive to maintain in-house; the best known may be

C.A. Evans and Associates. These topics are not discussed further here, but the ﬂavor

of this work can be obtained from the specialist books, especially Smith (1994); he too

worked for NPL, and gives a list of signiﬁcant papers by the above authors and others.

The brochures and web-sites of such organizations are an increasing resource, which

can be accessed via Appendix D.

A typical ‘surface science’ application of quantitative AES is to distinguish layer by

layer from other types of growth. Layer growth is a case which one can work out easily

92 3 Electron-based techniques

if we disregard (the minor) changes in the backscattering factor; the experimental ratio

is (I

) for a multilayer divided by (I

) for a ML. Here we assume that there are N

atoms in the ﬁrst layer, N

in the second and so on, and their spacing is d. Then we can

work out the signals at a coverage

between n and n11 ML from both the layers and

the substrate, as sums which take into account the attenuation. For example, if n51,

and we neglect attenuation within the ﬁrst layer

[(22

)1(

21)exp(2d/

cos

)]1N

, (3.15)

where the ﬁrst (second) term in square brackets correspond to the proportion of the

ﬁrst layer which is uncovered (covered) by the second layer, and so on. This relation

leads to a series of straight lines, often plotted as a function of deposition time, from

which the

can be deduced in favorable cases.

The simplest case, where there are the same numbers of atoms in each completed

ML, can be worked out explicitly. In that case, the slope of the second ML line ratioed

to that of the ﬁrst ML gives exp(2d/

cos

), from which d/

can be extracted if the

eﬀective analyzer angle

is known. This eﬀective angle is given by

cos

5(1/

)

兰兰

cos

·sin

, (3.16)

with the integrals taken over the analyzer acceptance. For detailed studies, it is advis-

able to construct computer programs which take the analyzer geometry into account,

and then perform the angular integration numerically. There has been much discussion

over what

really is in such experimental comparisons; it is now accepted to be the

attenuation length (AL), which is shorter than the imfp due to elastic (wide angle) scat-

tering (Dwyer & Matthew 1983, 1984, Jablonski 1990, Matthew et al. 1997, Cumpson

& Seah 1997). However, as pointed out by the last authors, unless the integration of

(3.16) is performed separately (as implied here), the AL also depends on the type of

analyzer used and the angular range accepted; thus in some papers the AL is not a

material constant, and one should beware of using published values uncritically.

There are many layer growth analyses in the literature, in some cases with a large

number of data points showing relatively sharp break points at well-deﬁned coverage,

such as for Ag/W(110) (Bauer et al. 1977). Experiments with fewer data points can still

lead to ﬁrm conclusions, using the comparison with a layer growth curve of the type

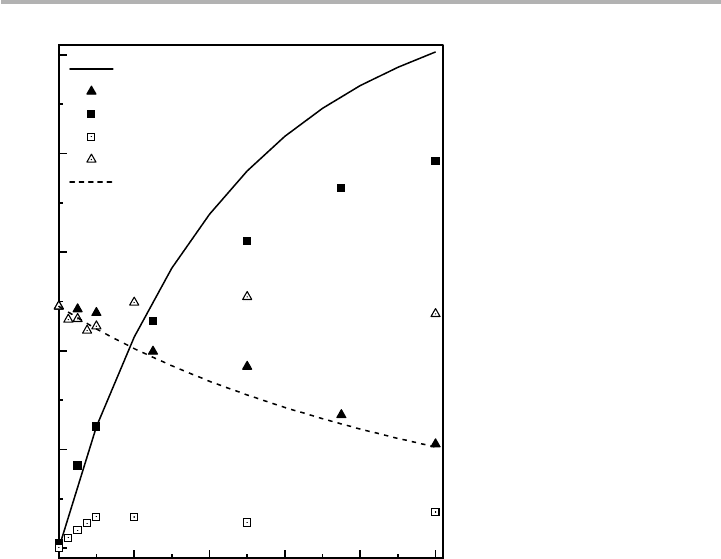
reported here. Such an analysis is shown in ﬁgure 3.20, which shows both the Auger

spectra for a series of Ag deposits on Si(001) and the corresponding Auger curves as a

function of coverage at both room and elevated temperature (Hanbücken et al. 1984,

Harland & Venables 1985). This is a case where growth more or less follows the ‘layer

plus island’, or Stranski–Krastanov (SK) mode, discussed in more detail in chapter 5.

From the Auger curves we see that at room temperature, layer growth is followed for

approximately 2 ML, but then experiment diverges from the model, indicating rough-

ening or islanding. The high temperature behavior is much more extreme, as the ﬁrst

layer is #0.5 ML thick, and islands grow on top of, and in competition with, this dilute

layer (Luo et al. 1991, Hembree & Venables 1992, Glueckstein et al. 1996).

The Ag/Si(111) and Ag/Ge(111) systems have also been studied, with the 冑3 recon-

structed layer at high temperatures having a thickness of around 1 ML. The exact

3.4 Quantiﬁcation of Auger spectra 93

coverage of such layers has been quite controversial (Raynerd et al. 1991, Metcalfe &

Venables 1996, Spence & Tear 1998), because the layers are only slightly more stable

than the islands, and consequently kinetic eﬀects play an important role. There are now

many examples, from these and other growth systems, which show characteristic Auger

curves associated with layer, island and SK growth. It is only by detailed quantitative

analysis, with for example known imfp values, that one can make such deﬁnitive state-

ments from Auger curves on their own.

Some recent examples are discussed by Li et al. (1995), Venables et al. (1996),

Venables & Persaud (1997) and Persaud et al. (1998), where the layer growth analysis

was used to investigate interdiﬀusion in Fe/Ag/Fe(110) and surface segregation in

Si/Ge/Si(001) hetero-structures. The purpose of a detailed layer growth analysis is

often to show that the system does not follow the layer growth mode, as discussed for

these cases in sections 5.5.3 and 7.3.2. Many authors have used deposition time as the

dose variable, and then state that the break point corresponds to 1 ML coverage; this

is unfortunately bad logic, since the coverage is the independent variable and the Auger

94 3 Electron-based techniques

Figure 3.20. Auger E·N(E) peak intensities versus coverage for Ag/Si(001) at deposition

temperatures T5293 K (closed squares for Ag and triangles for Si) and at T5773 K (open

symbols). The lines are numerical layer growth calculations using the actual analyzer geometry

and for an inelastic mean free path

50.82nm for Ag (355eV) in Ag (solid line) and

51.90nm for Si (1620 eV) in Ag (dashed line) (after Hanbücken et al. 1984, replotted with

permission).

0246810

200

400

600

800

1000

Ag (0.82 nm)

Si KLL (RT)

Ag LMM (RT)

Ag LMM (793 K)

Si KLL (793 K)

Si (1.9 nm)

Peak height (arb. units)

Ag coverage (ML)

intensity is the dependent variable. Used in the way described here, the Auger curve

needs to be calibrated independently, e.g. via a quartz oscillator or Rutherford back-

scattering spectroscopy (RBS), as discussed, for example, by Feldman & Mayer (1986).

3.5 Microscopy-spectroscopy: SEM, SAM, SPM, etc.

3.5.1 Scanning electron and Auger microscopy

Scanning electron microscopy (SEM) is now a routine tool which has been extensively

commercialized; many experimental scientists need access to a high performance, but

non-UHV, SEM. For example, in nanotechnology, the sizes of the structures are so

small that they cannot be seen with optical microscopes; SEM is often the easiest

choice to obtain better resolution. Electron beam lithography is an important fabrica-

tion technique, particularly for mask manufacture, and SEM is used routinely in

quality control of the devices produced in this (and other) ways. Via my son’s profes-

sion in biology/biochemistry, I have seen that SEM pictures of cells and cell organiza-

tion have taken a central place in even the introductory text books on these subjects.

Thus SEM is in danger of being taken for granted, due to the life-like, apparently 3D

images which are so readily produced. At the same time, contrast mechanisms are typ-

ically not understood in detail, due to the relatively complex nature of secondary elec-

tron production in solids and the ill-deﬁned collector geometry.

In a UHV, clean surface environment, there are several SEM-based techniques which

are surface sensitive at the ML and sub-ML level. The main SEM signal is based on col-

lecting secondary electrons, which typically form a large proportion of the emitted elec-

trons (see ﬁgure 3.7). In several papers with collaborators, we have shown that the low

energy secondary electron signal is very sensitive to work-function and other surface-

related changes; by biasing the sample negative to a bias voltage V

between 210 and

2500V, we can obtain biased secondary electron images (b-SEI), and ML and multi-

layer deposits can be readily visualized and distinguished (Futamoto et al. 1985). UHV-

SEM is particularly useful when combined with AES and RHEED (Venables et al.

1986, Ichikawa & Doi 1988). Progress in understanding secondary electron contrast

mechanisms, including in a clean-surface context, has been reviewed by Howie (1995).

Scanning Auger microscopy (SAM) is the child of AES and SEM. A ﬁne primary

beam is used, scanned sequentially across the sample at positions (x,y) as in SEM, and

the emitted electrons are energy analyzed as in AES. We can now (attempt to) perform

various types of analysis, such as a spot mode analysis (scan the analysis energy E at

ﬁxed (x

)), an energy-selected line scan (scan x at ﬁxed y

and analysis energy E

), or

an energy-selected map or image (scan x and y at analysis energy E

). These attempts

are subject to having a long enough data collection time and high enough beam current

to achieve a satisfactory SNR. Some examples are shown in ﬁgures 3.21 and 3.22. In

particular, you can notice that the SNR of the b-SE linescans is very good, and the b-

SE images are reasonably clear; next good are the energy-selected line scans. The most

diﬃcult/time-consuming are energy-selected images, especially if diﬀerence images are

3.5 Microscopy-spectroscopy 95

96 3 Electron-based techniques

Figure 3.21. Biased secondary electron images of 5 ML Ag/W(110), deposited past a mask

edge at T5 673 K and deposition rate R50.5 ML/min, observed with a 30 keV probe beam at

570°; the tilt is around the horizontal axis, so the vertical scale is compressed by cosec

(a) Zero bias, with Ag islands showing dark, and the layers essentially invisible; (b) bias

voltage V

52200V, showing the islands bright, and the 1 and 2 ML steps clearly visible (after

Jones & Venables 1985, reproduced with permission).