Venables J. Introduction to Surface and Thin Film Processes

Подождите немного. Документ загружается.

An isobar is a graph/cut/contour at constant pressure, giving a plot of

(T), with

ln(p) or

as the parameter. The meaning is the same as used on weather charts, but

the context is a little diﬀerent (is the weather an equilibrium phenomenon?). In many

single surface experiments, a more or less directed beam is aimed at the substrate to

establish a steady state concentration which is almost a true equilibrium, but not quite.

In particular, the temperature of the beam T

is typically not the same as that of the

adsorbate T

; the question of whether or not to correct the pressure for this thermo-

molecular eﬀect, of order (T

)

1/2

, recurs in the experimental literature.

An isostere is a contour on a p(T ) plot at constant coverage. Typically log(p) varies

as 1/T, and the energy associated with such an Arrhenius plot is called the isosteric heat

of adsorption. This is the energy associated with the adsorbed phase at that coverage,

and it comprises the adsorption energy and lateral binding energies, their derivatives

4.3 Phase diagrams and phase transitions 117

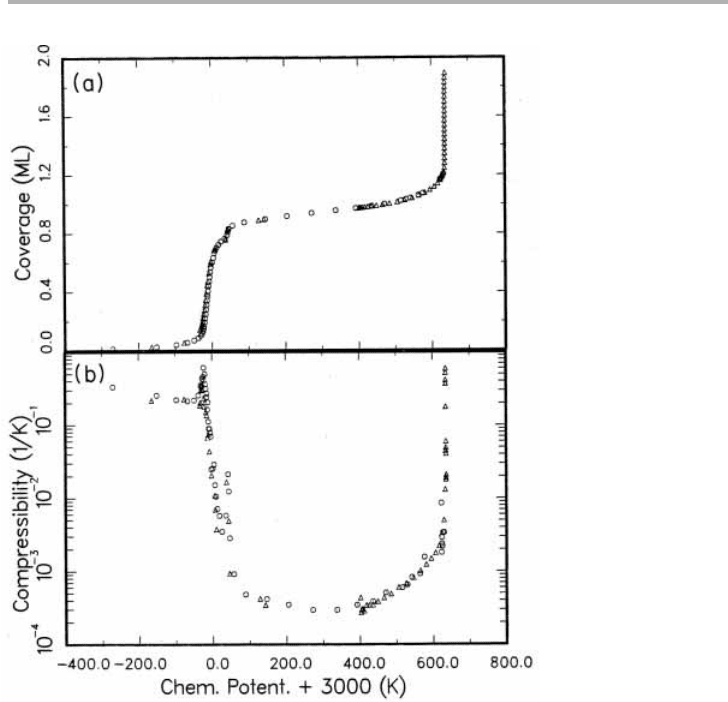
Figure 4.5. (a) Isotherm and (b) compressibility on a logarithmic scale in the monolayer and

bilayer region of Xe on graphite at T5105.4 K. Note the large range and high measured

accuracy of compressibility, and the reproducibility of two runs taken at T5105.456 and

105.435 6 0.001 K, with absolute values 6 0.1 K (from Gangwar et al. 1989, reproduced with

permission).

with respect to coverage, and various terms related to the atomic vibrations (as you

would by now expect).

4.3.2 Adsorption out of equilibrium with the gas phase

The examples of physisorption, discussed above, are typically, but not always, in equi-

librium with the gas phase. In these cases the state of the system depends on T, and

also on p. But at low T, exchange with the gas phase can be extremely, even inﬁnitesi-

mally, slow. Phase diagrams which use

and T as axes are favored by experimentalists

in chemisorption, and more generally at low T, where the pressure goes exponentially

to zero. Often in these diagrams the pressure is not known, and there may thereby be

some uncertainty about the true nature of the equilibrium. In this case, which can

occur for physisorption and frequently occurs for chemisorption, the gas pressure is

not only immeasurably low, but is irrelevant for discussion of the behavior of the

system.

Typically such systems are treated as closed 2D systems, the equilibrium (or lack of

it) with the 3D gas being ignored. This is reasonable for dissociative chemisorption at

low and moderate temperatures, owing to the very high adsorption energy of the

atoms: they are literally conﬁned to the surface layer. A metal–metal chemisorption

example where the equilibrium with the gas is taken into account at higher tempera-

ture is the AES and work function (D

) data for Au/W(110) (Kolaczkiewicz & Bauer

1984). In this data, AES is sensitive to the total Au coverage

within the ﬁrst ML, but

depends on whether the atoms are in the form of large islands (

higher) or as iso-

lated adatoms (

lower). Thus the data are suﬃcient to map out the 2D gas–2D solid

phase equilibrium on a

–T plot.

Two examples from the recent physisorption literature will be suﬃcient to illustrate

these various points. There have been several sets of experiments where sub-ML

amounts of Xe have been condensed onto metal surfaces. One of these involved STM

experiments at liquid helium temperatures (4 K), where the STM tip was used to move

the Xe atoms over the surfaces and construct the impressive if somewhat predictable

IBM (Eigler & Schweizer 1990). Xe/Ni(110) is a typical physisorption system, yet at

4 K the atoms stay where they are pushed/put for hours, and never leave the surface

during the duration of the experiment, unless one engages in (again non-equilibrium)

experiments to pick them up and transport them with the STM tip.

A second example is the detailed T-dependent study of Xe/Pt(111) (Horch et al.

1995). Good STM pictures could be produced below about 30 K, where nuclei of solid

ML Xe were shown to grow; above this temperature, however, STM pictures were

blurred, due to the motion of Xe atoms over the surface. This temperature is well below

that needed for Xe to desorb from the surface – only then is the full equilibrium state

obtainable. Note that observations of the average structure are then quite possible with

diﬀraction techniques, but that observation of the local structure by STM is impos-

sible. At low T, what we are observing is really the ﬁrst stage of Xe crystal growth,

rather than equilibrium adsorption. Another way to look at this is to note that we can

have a local equilibrium within the 2D system at lower temperature than that needed

118 4 Surface processes in adsorption

for full 3D equilibrium: this point recurs when considering models of (epitaxial) crystal

growth in chapter 5 and section 7.3. Chemisorption examples are discussed in section

4.5.

4.4 Physisorption: interatomic forces and lattice dynamical models

4.4.1 Thermodynamic information from single surface techniques

Once one applies ‘single surface’ techniques to adsorbed layers with sub-ML sensitiv-

ity, several types of phase and phase transition can be observed on many materials; the

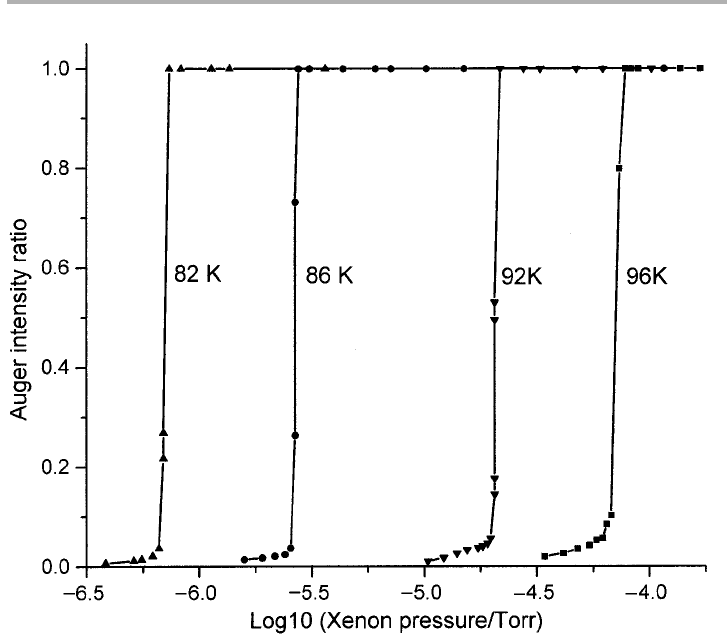
following examples are highly selective towards rare gases on graphite. Figure 4.6 shows

the AES amplitude for Xe/graphite as a function of log(p). These curves are adsorption

isotherms, taken as the pressure is varied through the gas–solid transition. The ﬁrst

order character of the transition is seen very clearly. At the same point that the AES

amplitude jumps, spots appear in LEED (or other diﬀraction technique) characteristic

4.4 Physisorption 119

Figure 4.6. AES amplitude of Xe/graphite as a function of log(p), showing a ﬁrst order

gas–solid phase transitions at p and T values indicated (after Suzanne et al. 1973, 1974, 1975,

reproduced with permission).

of an ordered ML solid. Understanding the thermodynamics of this 2D gas–solid tran-

sition enables one to measure both the cohesive energy of the 2D adsorbed solid, and

the pre-exponential factor, which can be related to the entropy of adsorption. This

results in an estimate of the change in vibration frequencies between the adsorbed 2D

phase and the bulk 3D phase. In this case, the entropy is negative, corresponding to the

eﬀective vibration frequencies being higher in the adsorbed state than the bulk phase

(Suzanne et al. 1974, 1975).

We can see how this arises by reference to the vapor pressure equation introduced in

section 1.3.1, coupled with the discussion of monolayer vibrations in section 4.2. The

2D gas–solid phase transition line on an Arrhenius plot has a slope measured experi-

mentally as 2780 6 50 K/atom, and this corresponds approximately to the sublimation

energy L

of the 2D solid phase. We note that this is considerably higher than the

(T50) sublimation energy L

51937 K/atom of 3D bulk Xe given in chapter 1, table

1.1, which is the basic reason why the adsorbed layer is stable.

The intercept of this 2D transition line on the log(p) axis at T

50 is actually higher

than that of the 3D bulk sublimation line intercept, and the diﬀerence in ln(p)

52DS/k, where DS is the entropy diﬀerence between 2D and 3D solids. This has also

been measured as DS5– 2 6 1 cal/mole/K, or in more useful units, DS/k521.0 6 0.5.

In the high temperature limit of the Einstein model (see equations 1.14 and 4.6), we

can see that DS/k53ln(

), where

is the geometric average of three vibration fre-

quencies in the 2D adsorbed solid. Thus, taking

50.73 THz from chapter 1, table 1.1,

we can estimate

as ⬃1.0 THz, with of course a substantial error bar; the error limits

indicate 0.86,

,1.20 THz. The vertical vibration frequency has been measured by

interpreting the hydrogen atom scattering Debye–Waller factor for Xe/graphite, as 0.90

THz (Ellis et al. 1985). Consequently, the thermodynamic DS/k estimate implies that

the lateral vibrations in the completed solid ML are also higher than bulk values.

Although this is consistent with the compression of ML solid Xe at low temperatures,

such a result is not inevitable. For example, a non-compressed sub-ML solid may well

have a larger DS than the 3D counterpart at low temperatures, due to low-lying vibra-

tional and translational modes.

The thermodynamics of these models are given in several places (e.g. Cerny 1983 or

Price & Venables 1976); many have referred to earlier work by Lahrer (1970). This last

reference is a relatively rare example of a Ph.D. thesis which was widely circulated, but

which never appeared in the same form in the open literature. Because they are not gen-

erally available, some of the more useful thermodynamic relationships are reproduced

here in Appendix E.2.

4.4.2 The crystallography of monolayer solids

The crystallography of the 2D solid phase of Xe/graphite was observed by diﬀraction

techniques (LEED and THEED). The THEED work had high enough precision to

detect that this solid was incommensurate (I), having a lattice parameter some 6–7%

larger than graphite under the conditions of ﬁgure 4.6. At lower T and p, these experi-

ments showed that the layer was compressed into a commensurate (C) phase, i.e. an

120 4 Surface processes in adsorption

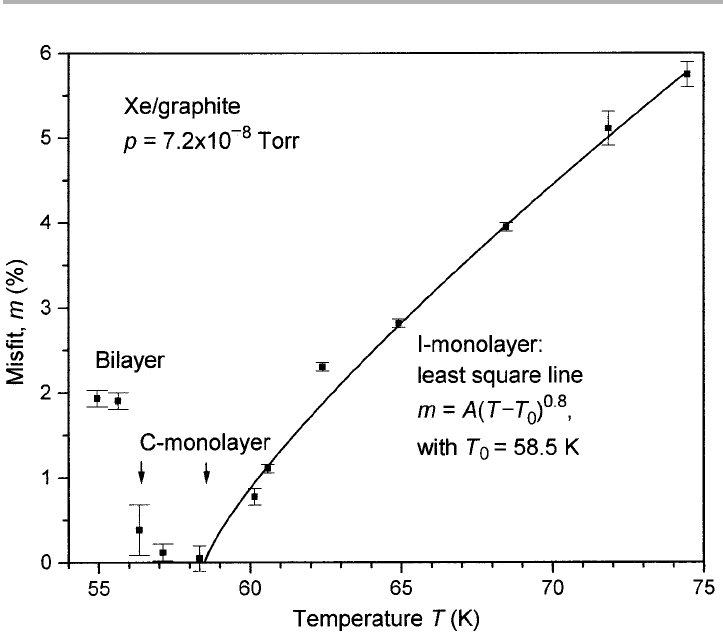
I–C phase transition was observed, as shown in ﬁgure 4.7 (Schabes-Retchkiman &

Venables, 1981, Kariotis et al. 1987, Hamichi et al. 1989, 1991). The opposite situation

happens for Kr/graphite: Kr ﬁrst condenses into the C-phase, and then compresses into

the I-phase, where the Kr lattice parameter is a bit smaller than the corresponding

graphite spacing. This C–I transition was observed by both THEED and LEED.

The I-phase has a modulated lattice parameter; this gains energy from having more

of the adsorbate in the potential wells of the substrate, but costs energy in the alter-

nate compression and rarefaction of the adsorbate. For example, if we consider the

substrate to provide a template on which the adsorbed monolayer sits, then the inter-

action potential varies periodically, and can be expressed as a Fourier series:

V(r)5V

1兺

exp(ig·r), (4.14)

where the sum is over as many 2D reciprocal lattice vectors g as are needed to describe

the corrugation of the potential adequately. Typically, only one term in V

, consistent

4.4 Physisorption 121

Figure 4.7. I–C and monolayer–bilayer phase transitions for Xe/graphite as measured by

THEED, where the misﬁt is the diﬀerence in lattice parameter of the adsorbed layer relative to

the commensurate 冑3 structure. As the temperature is lowered at constant pressure

(p57.2 310

Torr) within the ML regime, the misﬁt decreases to zero at T⬃58 K. About 2 K

lower, the bilayer condenses with a misﬁt ⬃2% (after Kariotis et al. 1987, Hamichi et al. 1989;

reproduced with permission).

with the symmetry of the underlying lattice, is retained; this does not mean that higher

order components are not present in the potential, just that there is not enough detail

in the model to ﬁnd out more by comparison with experiment.

If the geometry of all these phases is not clear, a pictorial description of the I-phase,

and its representation in terms of domain walls, solitons or misﬁt dislocations, is shown

here in ﬁgure 1.17 (Venables & Schabes-Retchkiman 1978). There are in fact two types

of I-phase: the aligned (IA) phase and the rotated (IR) phase, with another possibility

of a phase transition. The IR phase was ﬁrst discovered for Ar/graphite using LEED

(Shaw et al. 1978), and is even more pronounced in the case of Ne/graphite shown in

ﬁgure 4.8 (Calisti et al. 1982).

In a rotated phase, the diﬀraction spots are split, corresponding to two domains

rotated in opposite directions. Why does this happen? The misﬁt is accommodated by

compression and rarefaction; but typically shear waves cost less energy than compres-

sion waves, so it pays to include a bit of shear if the misﬁt is large enough. This eﬀect

was ﬁrst described quantitatively as a static distortion, or mass density, wave

Novaco & McTague (1977), and has been further developed by several other workers

including Shiba (1979, 1980), as described by Bruch et al. (1997, chapters 3 and 5). The

energies/atom gained by rotation for the various rare gases on graphite are indicated in

ﬁgure 4.9. It is remarkable how small these energies can be, and still be suﬃcient to sta-

bilize the rotated phase; this is because of the large numbers of atoms in each domain,

and because the domain walls cannot act independently of their neighbors, unless they

are far apart. In that limit, we enter new regimes, such as a domain wall ﬂuid; but let’s

not get too complicated at this stage.

These observations mean we can get C–IA–IR transitions in sequence, which have

been observed for both Kr and Xe/graphite. In the case of Xe/graphite, a large body of

THEED data has been obtained at relatively low pressures, close to the C–IA and

IA–IR transitions; one data set is shown in ﬁgure 4.7. These C, IA and IR phases have

also been observed for Xe/Pt(111) using helium atom scattering (Kern et al. 1986). We

can also get 1D incommensurate, or ‘striped’ phases, where the misﬁt is zero in one

direction, and non-zero in the other. Then the symmetry is reduced, for example from

hexagonal to rectangular as observed for Xe/Pt(111) at low misﬁt. The reasons why

such striped phases occur (or not) depend on details of the domain wall interactions,

as discussed by Kern & Comsa (1988) and by Bruch et al. (1997, chapter 5).

Near to the C–IA transition, the lattice dynamics can be split into two components,

involving low-lying vibrational modes of the domain walls, and faster vibrations of the

atoms within their local cells. This is seen both in computer simulations (Koch et al.

1984, Schöbinger & Abraham 1985) and in various analytical models (Kariotis et al.

1987, 1988, Shrimpton & Joós 1989). For Xe/graphite, it was possible to use the posi-

tion of the transition in the (T, p ) plane, shown in ﬁgure 4.7, to determine the depth of

the potential well DV52616 3 K/atom; similar analyses have been attempted for

other adsorption systems. Here, DV is the diﬀerence in energy between the atoms in the

122 4 Surface processes in adsorption

Note that the acronym SDW is sometimes used for static distortion wave, but that SDW more usually

means spin density wave in relation to magnetic materials.

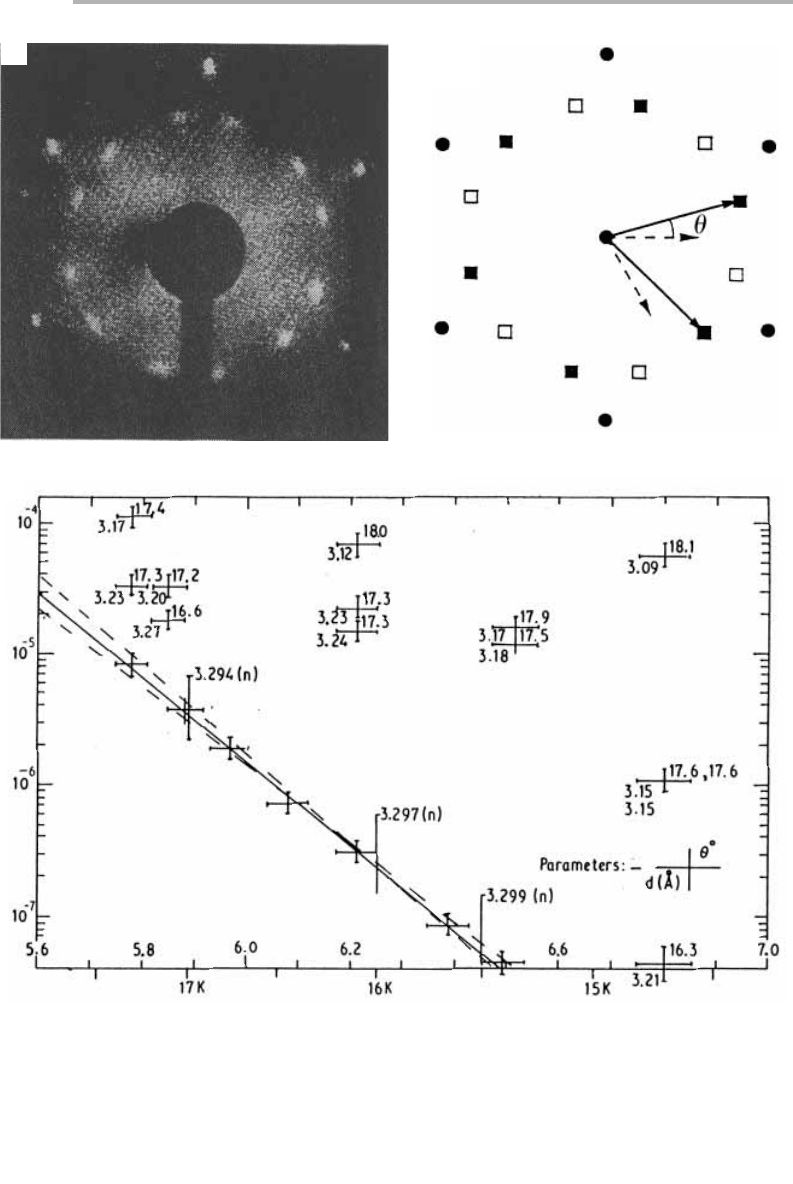
4.4 Physisorption 123

Figure 4.8. Rotated monolayer phases: the LEED pattern of (a) adsorbed Ne/graphite; (b)

schematic diagram of the diﬀraction spots from the two domains; (c) measurements of lattice

parameter and rotation (after Calisti et al. 1982, reproduced with permission).

(a)

(b)

(c)

center of the hexagon and on top of a carbon atom, which is some factor times

), introduced in section 4.2. By following through the algebra in problem 4.2,

one can evaluate this factor, and thereby show that (E

)536 K is a reasonable

value for the calculation presented in ﬁgure 4.1b. We can note in passing that the factor

relating DV to (E

) does depend on the assumption that only one Fourier

coeﬃcient V

is important in (4.14). The error involved in this assumption can be

explored further via problem 4.2.

4.4.3 Melting in two dimensions

There has also been much interest in the melting transition. The major question is

whether melting proceeds in two stages, via a hexatic phase, in which long range posi-

tional order is lost, but some ‘bond orientational order’ is preserved. Interest in this

topic is primarily due to the importance of liquid crystals, where the hexatic phase in

free-standing ﬁlms is well documented (Brock et al. 1989, Strandburg 1992).

Additional interest arises from regarding physisorbed monolayers as model 2D

systems, in which properties speciﬁc to two dimensions can be demonstrated. Melting

has been thought to be such a case, following an inﬂuential series of papers describing

the statistical mechanics of topological defects in ML systems. These papers

124 4 Surface processes in adsorption

Figure 4.9. Calculated energies as a function of rotation angle for the rare gases on graphite,

after Novaco & McTague (1977), reproduced with permission. Note the small energies

(0.5–2.5 K/atom) involved, which are nevertheless suﬃcient to stabilize the rotated phases.

(Kosterlitz & Thouless 1973, Halperin & Nelson 1978, Nelson & Halperin 1979, and

Young 1979), which together became known as KTHNY, formed a springboard for

subsequent work. The central idea was that dislocations that thread the ML are point

defects, which are present in thermal equilibrium. At low temperature, such defects

exist only in bound pairs, but they can unbind above a certain critical temperature.

In the context of the six-nearest neighbor hexagonal crystal structure of rare gas

layers, isolated point dislocations destroy translational order exponentially, but orien-

tational order decays more slowly as a power law. A high density of isolated, or free,

dislocations was identiﬁed with the hexatic phase. However, the cores of dislocations

themselves can unbind to produce disclinations, where the local orientational order is

alternately ﬁve- and seven-fold; if we have many of these, we have a true 2D liquid. The

questions arising were then whether the hexatic phase in general existed, and if so, what

was the order of the phase transitions. The role of computer simulation in this argu-

ment was interesting. These studies essentially always gave ﬁrst order transitions, but

theorists could always invoke ‘ﬁnite size eﬀects’ to claim that the sample size in the sim-

ulation was not large enough.

Experimental melting studies on Xe/graphite include thermodynamic studies

(Gangwar et al. 1989, Jin et al. 1989) and many sets of diﬀraction data. Our own

THEED studies of melting (Zerrouk et al. 1994) do indeed observe the hexatic phase

in a narrow temperature region. But it seems that the thermodynamic experiments are

most sensitive to the expansion involved in the hexatic–liquid transition, whereas

diﬀraction is most sensitive to orientation changes across the solid–hexatic transition.

Models are complicated by the fact the solid ML Xe melts from the aligned (IA) phase.

This means that the orientational order provided by the substrate, via the term V

(4.14), must be a signiﬁcant term in the free energy balance. Detailed discussions of

such systems have also emphasized the importance of the organization of dislocations

into grain boundaries (Venables & Schabes-Retchkiman 1978, Chui 1983), and the role

of anharmonicity (Joós & Duesbery 1985, Bruch et al. 1997). Both of these eﬀects tend

to cut oﬀ the second order transitions predicted by KTHNY, producing weakly ﬁrst

order transitions. These arguments tend to back the claims of computer simulations

(Abraham 1982), who claimed that disclination unbinding represents the highest T at

which the 2D solid can be metastable, rather than the thermodynamic melting temper-

ature; this type of argument can get quite heated!

One can appreciate that the details of all these phases and their transitions involve

competing interactions, often quite subtle. Physisorbed layers are thus test-beds for

exploring interatomic forces and dynamics at surfaces, and the rich variety of experi-

mental observations produce constraints on feasible models; however, the search for

truly 2D model systems with which to test the elegant theories is, from an experimen-

tal viewpoint, somewhat elusive.

4.4.4 Construction and understanding of phase diagrams

The combination of all the information from diﬀerent types of experiment into a

phase diagram is still very much a research project, but one which proceeds in ﬁts and

starts, depending on individual enthusiasm, patience and the availability of funds and

4.4 Physisorption 125

time. For example, the current Ne/graphite (log(p), 1/T) phase diagram dates from

Calisti et al. (1982). Phase diagrams (T,

) for Ar, Kr, and Xe/graphite are shown by

Zangwill (1988, chapter 11), and many examples of both types of diagram are given

in Bruch et al. (1997, chapter 6). Note how it is impossible to portray all the informa-

tion on these 2D cuts of the 3D (T,logp,

) data. With rotation, as shown for

Ne/graphite in ﬁgure 4.8(c), we have really four-dimensional information, and this has

only been mapped in the barest outline. Quantum cell models of Ne/graphite have

been developed by Bruch and by others in order to understand these results, as refer-

enced in Bruch et al. (1997).

For the heavier gases, the cell model works remarkably well, and this simple model

has been carried through for Kr and Xe/graphite (Schabes-Retchkiman & Venables,

1981) as shown in ﬁgure 4.10; parts of this diagram have been elaborated in later

papers. These diagrams show the expansion of the layers with increasing T at constant

p, and the compression of the layers with increasing p at constant T. The lines are iso-

steres, lines of constant coverage, or density as determined by the lattice spacing, where

n51 corresponds to the C-phase. As can be seen they are slightly steeper than the phase

transition lines. These diagrams are, however, by no means complete; there are now a

126 4 Surface processes in adsorption

Figure 4.10. Outline phase diagrams of (a) Kr/graphite and (b) Xe/graphite in a multi-

parameter potential model using Einstein vibrations for the vertical motion and the cell model

for lateral motion. The isosteres plotted have a coverage parameter n, where n51 corresponds

to the C-phase (one atom to every third graphite hexagon). Experimental points from the

literature (after Schabes-Retchkiman & Venables, 1981, reproduced with permission).

10 12 14 16 18 20

-8

-7

-6

-5

-4

-3

-2

-1

C-phase

1000/T (K

-1

)

0.90

0.89

1.0

Xe/graphite:

monolayer cell model

isosteres n = 0.89, 0.9 to 1.0,

∆

n = 0.02 ML

3D sublimation

Bilayer

sublimation

Triple

point

Cell model

calculation

Xe ML

sublimation

g (p/Torr)

10 12 14 16 18 20

-8

-7

-6

-5

-4

-3

-2

-1

C-phase

1000/T (K

-1

)

1.12

1.10

1.0

Kr/graphite:

monolayer cell model

isosteres n = 1.0 to 1.12,

∆

n = 0.02 ML

3D sublimation

Bilayer

sublimation

Triple

point

Cell model

calculation

Kr ML

sublimation

Log (p/Torr)

(a)

(b)