Васюков В.Н. Теория электрической связи

Подождите немного. Документ загружается.

2.10. Ряд Фурье и интеграл Фурье

Пример 2.22. Автокорреляционная

функция прямоугольного импульса дли-

тельности

имеет вид треугольника

(рис. 2.27).

Максимальное значение АКФ равно

, где

– амплитудное (максималь-

ное) значение импульса. ◄

Пример 2.23. С точки зрения точно-

сти синхронизации выгодно использовать

сигнал, который имеет «острую» (иголь-

чатую) АКФ, близкую по форме к -функции. Реальные сигналы с

конечной шириной спектра к этому идеалу могут только прибли-

жаться. Одним из хороших приближений является сигнал Баркера,

состоящий из

разнополярных прямоугольных элементарных им-

пульсов; пример такого сигнала при

5N 

показан на рис. 2.28, а.

Отличительное свойство сигнала Баркера состоит в том, что его

АКФ (рис. 2.28, б) имеет лепестковый вид, причем ширина каждо-

го лепестка равна удвоенной длительности элементарного импуль-

са, а уровни боковых лепестков в

раз меньше, чем уровень

главного лепестка (равный, очевидно,

). К сожалению, сиг-

налы Баркера существуют только при

 

2, 3, 4, 5, 7,11,13N 

. Та-

ким образом, максимальное превышение главного лепестка над

боковыми, которое определяет эффективность (помехоустойчи-

вость) синхронизации

, не может быть для сигналов Баркера

больше, чем 13. Бóльшее превышение достигается для длинных

последовательностей разнополярных прямоугольных импульсов,

называемых m-последовательностями (для них, однако, уровни бо-

ковых лепестков могут быть лишь в

раз меньше главного). ◄

x(t)

–

– 3

( )

а б

Рис. 2.28. Сигнал Баркера (

) и его АКФ

Чем больше указанное превышение, тем меньше вероятность принять боковой

лепесток за главный из-за шумовых выбросов.

–

( )

Рис. 2.27. АКФ прямо-

угольного импульса дли-

тельности

2. ОСНОВЫ ТЕОРИИ СИГНАЛОВ

2.11. ДИСКРЕТИЗАЦИЯ СИГНАЛОВ.

ТЕОРЕМА ОТСЧЁТОВ

Коэффициенты обобщенного ряда Фурье, составляющие

спектр некоторого сигнала относительно полного ортонормального

базиса, вычисляются путем скалярного умножения этого сигнала

на базисные функции. Существует счетный базис, для которого эта

операция эквивалентна взятию отсчѐтов мгновенных значений

аналогового сигнала через равные промежутки времени. Таким

образом, аналоговый сигнал однозначно представляется дискрет-

ной последовательностью своих отсчѐтов. Такая дискретизация

аналоговых сигналов имеет огромное значение для современной

техники, так как является основой цифровой обработки сигналов.

Следует сразу же отметить, что, как и базис Фурье, упомяну-

тый базис не обладает свойством полноты в пространстве

( , )L   

, поэтому он непригоден для представления с заданной

точностью любых аналоговых сигналов ограниченной энергии, од-

нако для подпространства сигналов, спектральная плотность кото-

рых сосредоточена на конечном интервале

 

вв

,FF

частотной

оси

, этот счетный базис полон.

Условие финитности спектра не является слишком обремени-

тельным, так как спектральные плотности всех сигналов из

( , )L   

при

f   

быстро убывают

, поэтому их можно

с любой точностью аппроксимировать финитными функциями.

При выборе конкретного базиса в качестве конечного интервала

 

вв

,FF

принимается так называемая эффективная ширина спек-

тра сигнала. Эффективной шириной спектра можно считать ши-

рину частотного интервала, в котором сосредоточена заданная до-

ля (например, 99 %) всей энергии сигнала. Обычно на практике

перед дискретизацией сознательно ограничивают ширину спектра

сигнала путем его предварительной фильтрации, так как это

уменьшает ошибку восстановления аналогового сигнала.

Возможность представления аналогового сигнала последо-

вательностью его отсчетов и условия применимости такого пред-

ставления устанавливаются теоремой отсчетов. Приведенное

Напомним, что такие функции называются финитными.

См. по этому поводу п. 2.10.2.

2.11. Дискретизация сигналов. Теорема отсчетов

ниже доказательство теоремы отсчетов принадлежит

В.А. Котельникову

Рассмотрим произвольный сигнал

()xt

, спектральная плот-

ность которого

()Xf

равна нулю вне конечного интервала

 

вв

,FF

частотной оси. Выразим функцию спектральной плотно-

сти

()Xf

в виде ряда Фурье

()

j kf

X f C e









, (2.55)

вполне аналогичного комплексному ряду Фурье (2.39), представ-

ляющему временнýю функцию на интервале

 

2, 2TT

, с той

очевидной разницей, что базисные функции здесь зависят не от

а от

. Очевидно, коэффициенты ряда находятся как

()

j kf

C X f e df







,k   

Выразим сигнал

()xt

через его обратное преобразование Фу-

рье, подставляя в качестве спектральной плотности еѐ представле-

ние рядом Фурье (2.55)

вв

( ) ( )

j f t k

j ft

x t X f e df C e df

















  





cos 2

C f t k df











  













sin 2

F t k































. (2.56)

Владимир Александрович Котельников (1908–2005) – выдающийся русский

инженер и математик; доказал теорему отсчетов в 1933 г. Известны также ва-

рианты доказательства теоремы отсчѐтов, связанные с именами Э. Уиттекера

(1916), Х. Найквиста (1928), Д. Габора (1946), К. Шеннона (1948).

2. ОСНОВЫ ТЕОРИИ СИГНАЛОВ

Заметим, что

()

j kf

C X f e df







вв

()

j ft

X f e df



















. (2.57)

Подставив (2.57) в (2.56) и введя обозначение для интервала

(шага) дискретизации



, запишем сигнал в виде ряда

 

sin sin

()

t kT t nT

x t x kT x nT

t kT t nT



 

   



   

   

  





(2.58)

известного под названием ряда Котельникова. Коэффициенты

 

x nT

этого ряда представляют собой отсчеты (мгновенные

значения) аналогового сигнала

()xt

, взятые через равные про-

межутки времени



. Базисные функции ряда Котельни-

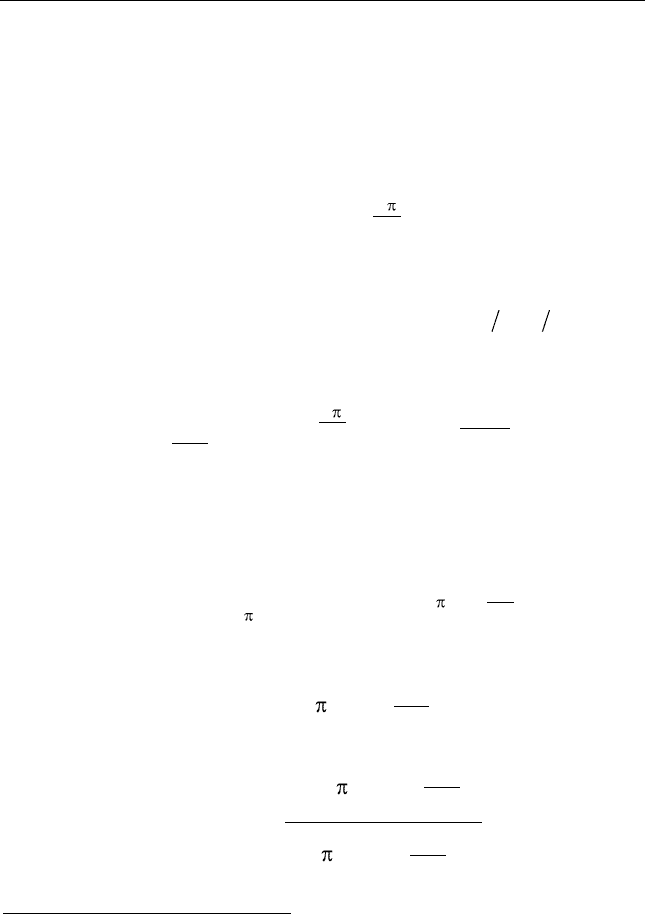
кова получаются сдвигами на такие же промежутки времени

единственной функции. Обозначим эту исходную функцию

( ) sin

t t t

   



   

   

, тогда базис будет совокупностью

 

( ), ,

  

( ) ( )

t t nT

. Несколько базисных функ-

ций показаны на рис. 2.29. Этот ряд даѐт точное представление

(интерполяцию) значений сигнала

()xt

в любой точке

временнóй оси по известным значениям сигнала в дискретном

множестве еѐ точек (узлов интерполяции). Следовательно, нет

необходимости передавать или хранить всѐ непрерывное множе-

ство (континуум) значений аналогового сигнала с финитным

спектром, достаточно передать (или зафиксировать на некото-

2.11. Дискретизация сигналов. Теорема отсчетов

ром носителе) счетную последовательность его дискретных от-

счетов

 

 

[ ] , ,

x n x nT n   

, по которым при необходимости

сигнал может быть точно восстановлен.

()

Рис. 2.29. Базисные функции ряда Котельникова при

n = – 1, 0, 3, 7

Чтобы выяснить свойства полученного базиса, найдем скаляр-

ное произведение пары базисных функций. Сравним выражения

(2.56) и (2.55) для сигнала и его спектральной плотности. Очевид-

но, функция

sin 2

F t k























имеет спектральную плотность, равную

j kf

на частотном ин-

тервале

 

вв

,FF

, и нулю вне его. Тогда согласно обобщенной

формуле Рэлея скалярное произведение

-й и

-й функций бази-

са Котельникова равно

()

( , )

j k m f

k m km

e df







Таким образом, базис Котельникова ортогонален, но не норми-

рован. По существу, базис Котельникова во временной области –

это базис Фурье в частотной области [ср. (2.55) и (2.56)]. Поэто-

му свойства ортогональности и полноты одинаково справедливы

для этих базисов.

Чтобы восстановить (интерполировать) аналоговый сигнал по

последовательности его отсчетов, необходимо просуммировать все

2. ОСНОВЫ ТЕОРИИ СИГНАЛОВ

базисные функции Котельникова при

,n   

с весовыми коэф-

фициентами, равными отсчѐтам

 

x nT

. Технически эту операцию

можно в принципе осуществить, располагая ЛИС-цепью, имеющей

импульсную характеристику, совпадающую с функцией Котельни-

кова

()t

, и подавая на вход этой цепи в моменты

nT n   

воздействия в виде -функций с амплитудными множителями

 

x nT

,n   

. Следовательно, на вход такой цепи должен по-

даваться возбуждающий сигнал в виде

-периодической после-

довательности -функций, умноженных на отсчеты аналогового

сигнала

( ) ( ) ( )

v t x nT t nT









. Откликом цепи на воздействие

()

t nT

является сдвинутая на

импульсная характеристика

( ) ( )

t t nT

. С учетом линейности и стационарности цепи

очевидно, что отклик на воздействие

()vt

представляет собой пра-

вую часть выражения (2.58), поэтому на выходе цепи наблюдается

восстановленный сигнал

()xt

Учитывая, что -функция имеет нулевую длительность, можно

представить возбуждающий сигнал в виде

( ) ( ) ( ) ( ) ( ) ( ) ( )

d d d

v t x nT t nT x t t nT x t t



 

    





, (2.59)

где

( ) ( )

t t nT











– периодическая последовательность

-функций. Считая (нестрого!) -функцию «коротким импуль-

сом», можно назвать сигнал

()vt

идеализированным сигналом с

амплитудно-импульсной модуляцией (иАИМ-сигналом). Посколь-

ку иАИМ-сигнал равен произведению (2.59), его спектральная

плотность равна свертке спектральных плотностей сигналов

()xt

()t



. Найдем спектральную плотность последовательности

()t



Для этого вначале запишем

-периодическую последователь-

ность в виде ряда Фурье

()

j nt

t S e











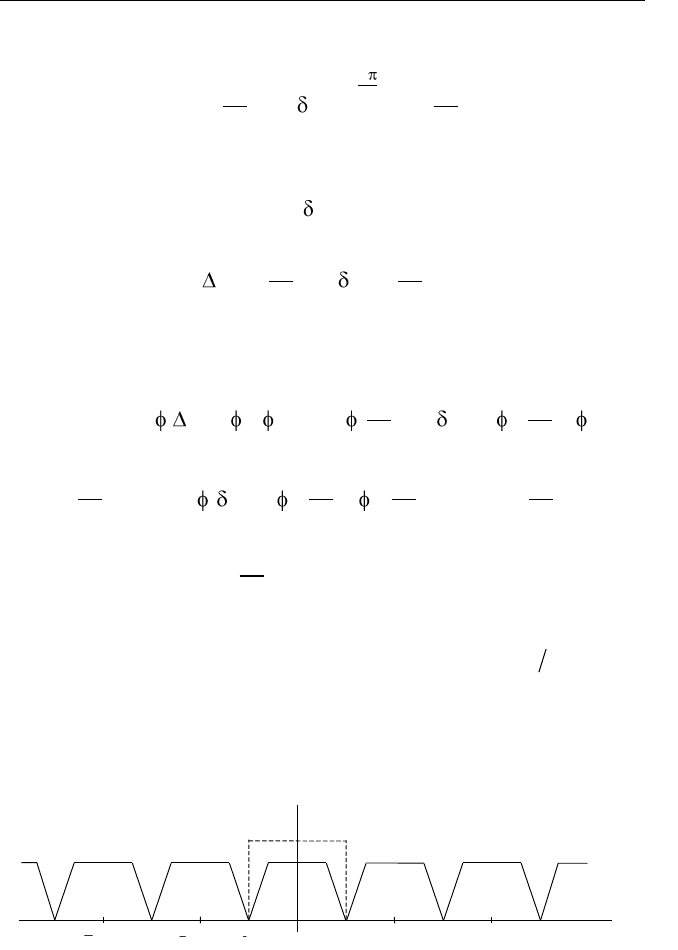
2.11. Дискретизация сигналов. Теорема отсчетов

коэффициенты которого, определяемые согласно (2.41), равны:

()

j nt

S t e dt







Поэтому, учитывая выражение (2.52), запишем спектральную

плотность последовательности

()t



в виде

()

















Теперь найдем спектральную плотность иАИМ-сигнала как

свертку:

( ) ( ) ( ) ( )

V f X f d X f d







 



     











()

d d d d

X f d X f

T T T T





 



   

     

   

   





()

X f nF









Таким образом, спектральная плотность иАИМ-сигнала пред-

ставляет собой с учетом масштабного коэффициента

сумму

(суперпозицию) бесконечного множества копий спектральной

плотности аналогового сигнала

()xt

, отличающихся друг от друга

сдвигами по оси частот, кратными частоте дискретизации

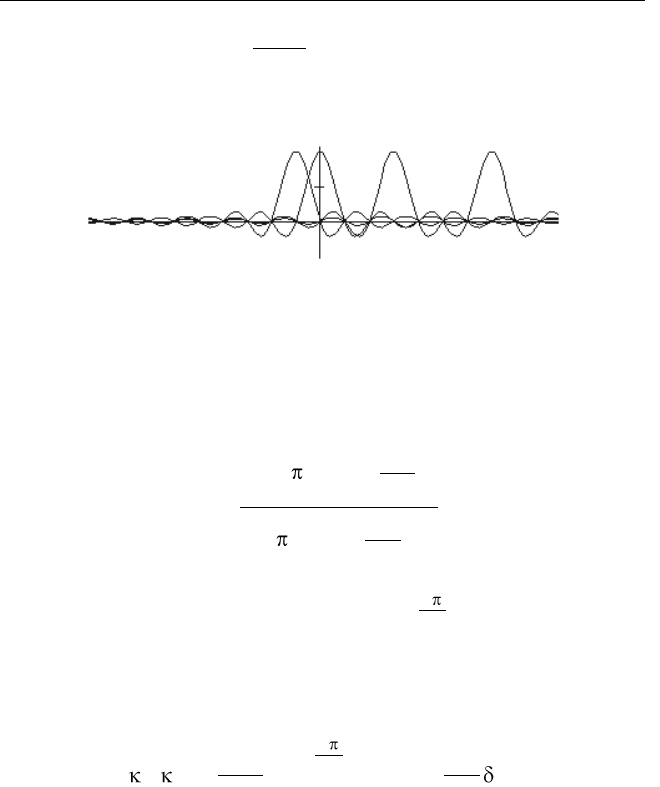
(рис. 2.30).

( ), ( )V f H f

Рис. 2.30. Спектральная трактовка восстановления сигнала

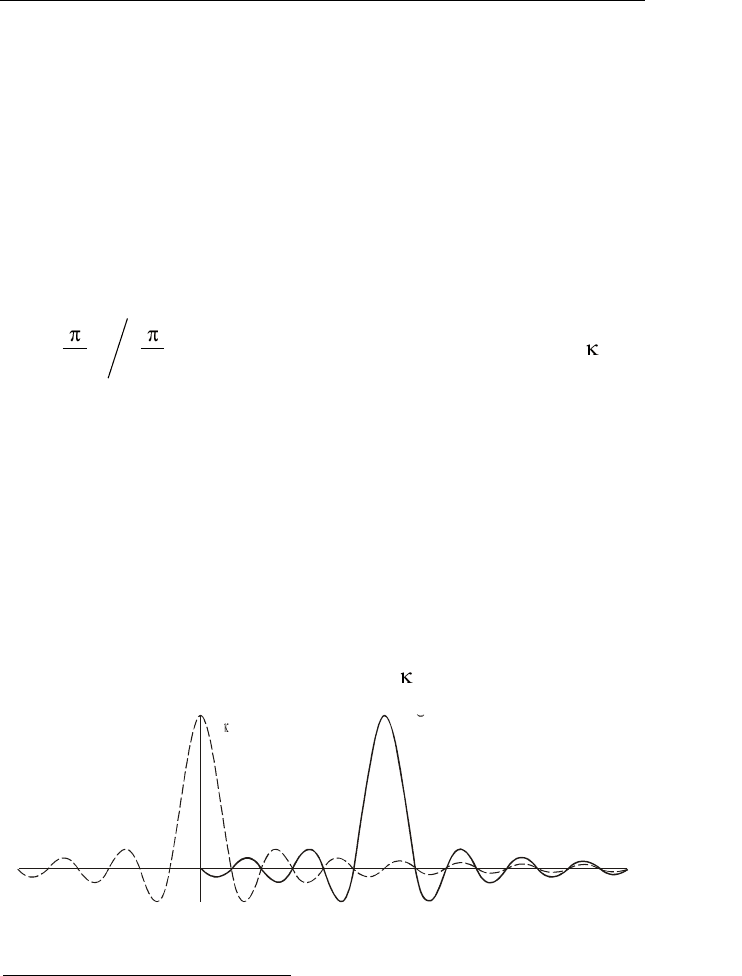
2. ОСНОВЫ ТЕОРИИ СИГНАЛОВ

Следовательно, восстановление аналогового сигнала интерпо-

лирующей цепью равносильно подавлению в спектре сигнала

()vt

всех спектральных составляющих, не принадлежащих интервалу

 

вв

,FF

, поэтому интерполирующий фильтр должен иметь

П-образную (прямоугольную) комплексную частотную характери-

стику (на рис. 2.29 показана штриховой линией):

вв

, ,

()

0 в противном случае.

T F f F

  









(2.60)

Легко убедиться, что идеальная интерполирующая цепь должна

в таком случае иметь импульсную характеристику

()ht 

sin

   











, совпадающую с базисной функцией

()t

Таким образом, спектральный подход к восстановлению аналого-

вого сигнала по его отсчетам приводит к тому же выводу, что и

временной.

Идеальная интерполирующая цепь, строго говоря, нереализуе-

ма, так как еѐ импульсная характеристика имеет бесконечно боль-

шую протяженность в области отрицательных времен. Однако в

принципе можно построить цепь, сколь угодно точно еѐ аппрокси-

мирующую, правда, при этом восстановленный сигнал будет полу-

чаться с задержкой (тем бóльшей, чем выше требуемая точность

аппроксимации)

. В самом деле, физическая реализуемость пред-

полагает каузальность импульсной характеристики, т.е. выполне-

ние условия (2.34). На рис. 2.31 показаны импульсная характери-

стика идеальной интерполирующей цепи

()t

(штриховая линия)

(t)

ht( )

Рис. 2.31. Аппроксимация импульсной характеристики интерполирующей

цепи

Сложность цепи при этом также возрастает.

2.11. Дискретизация сигналов. Теорема отсчетов

и аппроксимирующая ее функция

()ht



(сплошная линия). Очевид-

но, при соблюдении условия каузальности повышение точности

аппроксимации неизбежно приводит к сдвигу функции вправо, а

значит, увеличивает задержку восстановленного сигнала.

Нереализуемым является и сигнал, описываемый выражением

(2.59), так как в него входят -функции. На практике вместо них

используются короткие

импульсы.

Необходимо отметить, что выражение (2.59), описывающее

процесс восстановления аналогового сигнала по его отсчетам, ино-

гда неправильно связывают с процессом дискретизации сигнала.

На самом деле взятие (одиночного) отсчета аналогового сигнала в

произвольный момент времени

представляет собой стробиро-

вание и описывается выражением типа свертки

0 0 0

( ) ( ) ( ) ( ) ( )x t x t t t dt x t t t dt



 

   



, (2.61)

а не умножения, как в (2.59).

Реальное взятие отсчета производится устройством, в котором

выполняется свертка аналогового сигнала не с -функцией, как в

выражении (2.61), а с некоторым реальным импульсом

()dt

. Этот

импульс должен быть «похож» на -функцию, в частности, он

должен быть коротким и интеграл от него должен быть равен 1.

Для простоты примем в качестве

()dt

прямоугольный импульс

длительности и амплитуды

. Свертке сигнала

()xt

с таким

импульсом соответствует умножение спектральной плотности

()Xf

на спектральную плотность прямоугольного импульса,

имеющую, как известно, форму функции вида

sin /xx

, поэтому

при стробировании реальным импульсом конечной длины всегда

происходит искажение спектра сигнала. Для уменьшения такого

искажения необходимо стремиться к уменьшению длительности

импульса

()dt

, при этом форма импульса не играет заметной роли.

Все реальные сигналы имеют конечную длительность, поэтому

спектральная плотность реального сигнала не может быть фи-

нитной. Нефинитность спектра сигнала приводит к тому, что «хво-

сты» копий спектральной плотности

()Xf

при периодическом

Здесь импульс считается коротким, если его длительность много меньше вели-

чины

1/ F

2. ОСНОВЫ ТЕОРИИ СИГНАЛОВ

повторении накладываются друг на друга и суммируются, приводя

к необратимому искажению сигнала

. Применяемая до дискрети-

зации фильтрация сигнала при помощи фильтра нижних частот с

характеристикой, близкой к прямоугольной, подавляет эти «хво-

сты», уменьшая погрешность интерполяции.

Итак, точному восстановлению аналогового сигнала по после-

довательности его отсчѐтов препятствуют:

1) конечная длительность любого реального сигнала и, как

следствие, бесконечная ширина его спектра;

2) конечная длительность реального стробирующего импульса

и, как следствие, искажение формы спектра сигнала при дискрети-

зации;

3) невозможность точно реализовать интерполирующий

фильтр.

Несмотря на эти ограничения, дискретизация широко применя-

ется на практике, в частности, она является необходимой частью

цифровой обработки сигналов.

2.12. АНАЛИТИЧЕСКИЙ СИГНАЛ

В теории электрических цепей, как известно, широко исполь-

зуется метод представления гармонических колебаний комплекс-

ными векторами (метод комплексных амплитуд), состоящий в том,

что гармоническое колебание

cos(2 )

U ft 

рассматривается как

вещественная часть комплексной функции

(2 )j ft



, которая

изображается вектором в комплексной плоскости, вращающимся с

постоянной угловой скоростью

2 f

; при этом вектор имеет

длину

и при

0t 

составляет с вещественной осью комплекс-

ной плоскости угол . Аналогичное представление можно ввести

для сигнала произвольной формы

( ) Re{ ( )}x t z t

где

( ) ( ) ( )z t x t j x t  

– комплексное колебание (аналитический

сигнал), мнимая часть которого

()xt

должна однозначно опреде-

ляться исходным сигналом

()xt

Это явление называется подменой частот; в англоязычной литературе исполь-

зуется название aliasing.