Васюков В.Н. Теория электрической связи

Подождите немного. Документ загружается.

2.9. Частотное описание ЛИС-цепей

ражение

( ) ( ) ( )Y f H f X f

, связывающее выходной сигнал ЛИС-

цепи с входным сигналом. Заметим, что это выражение соответст-

вует в конечномерном случае умножению вектора на диагональ-

ную матрицу (2.29).

Подытоживая, можно сказать, что представление входного сиг-

нала относительно собственного базисного ядра

2j ft



имеет пре-

имущество перед динамическим представлением, так как вместо

интегрального выражения свертки связь входного сигнала с вы-

ходным описывается произведением спектральных плотностей.

Уместно еще раз напомнить, что «естественное» временнóе пред-

ставление сигнала

()xt

– это также спектральная плотность,

только относительно ядра

()t 

Выражение

( ) ( ) ( )Y f H f X f

устанавливающее связь спектральных плотностей сигналов на вхо-

де и выходе ЛИС-цепи через еѐ комплексную частотную характе-

ристику, служит основой спектрального метода анализа линей-

ных стационарных цепей, широко используемого благодаря своей

простоте. Именно этим объясняется исключительная роль ряда и

интеграла Фурье в теории сигналов и цепей.

Функция

()Hf

в общем случае является комплексной,

()

( ) ( )

H f K f e

, что неудобно. Часто рассматривают еѐ модуль

и аргумент по отдельности, при этом модуль

( ) ( )K f H f

назы-

вают амплитудно-частотной характеристикой (АЧХ), а аргумент

()f

– фазочастотной характеристикой (ФЧХ) цепи.

Пример 2.18. RC-фильтр нижних частот, представленный на

рис. 2.18, имеет амплитудно-частотную характеристику и фазоча-

стотную характеристику, показанные на рис. 2.21.◄

(

)

( )

а б

Рис. 2.21. Амплитудно-частотная характеристика (а) и фазочастотная

характеристика (б) RC-фильтра нижних частот

2. ОСНОВЫ ТЕОРИИ СИГНАЛОВ

Значение комплексной частотной характеристики при заданной

частоте

может в принципе быть измерено как отношение сигна-

ла на выходе ЛИС-цепи к входному сигналу, если этот входной

сигнал – функция

2j ft



. Таким образом, функция

2j ft



при про-

извольно задаваемой частоте

может рассматриваться, как ис-

пытательный сигнал, позволяющий получить описание цепи

(КЧХ). Другим испытательным сигналом является -функция, ко-

торая могла бы быть использована для получения отклика цепи в

виде импульсной характеристики. Поскольку КЧХ и импульсная

характеристика связаны друг с другом взаимно однозначно (через

пару преобразований Фурье), должна существовать связь и между

соответствующими им испытательными сигналами. В самом деле,

-функция может рассматриваться как интегральная сумма одно-

временно воздействующих на вход цепи функций

2j ft



, так как еѐ

спектральная плотность

( ) 1

j ft

t e dt











Каждая из комплексных гармонических функций умножается

цепью на соответствующее значение КЧХ, поэтому импульсная

характеристика – отклик на -функцию

( ) ( ) 1

j ft

h t H f e df







  



представляет собой, образно говоря, «равнодействующую» откли-

ков на все такие функции.

Заметим, что указанные измерения КЧХ и импульсной харак-

теристики на практике точно выполнить нельзя. Даже если бы су-

ществовали абсолютно точные измерительные приборы, потребо-

валось бы бесконечное время для генерирования функций

2j ft



(нельзя забывать, что они определены на всей временнóй оси!) и

измерения отношений выходных сигналов к входным с бесконечной

точностью при всех значениях частоты

. В свою очередь, -функ-

ция представляет собой «бесконечно короткий импульс бесконечно

большой амплитуды», который также не может быть реализован

точно. На практике КЧХ и импульсная характеристика ЛИС-цепи

могут быть измерены приближенно с помощью отрезков гармониче-

ских испытательных сигналов конечной продолжительности и ко-

ротких импульсов большой (но конечной) амплитуды.

2.10. Ряд Фурье и интеграл Фурье

Часто в выражениях, связанных со спектральным анализом

сигналов и ЛИС-цепей, вместо частоты

используется круговая

частота

2 f

. Пара (2.18) – (2.19) преобразований Фурье в ре-

зультате замены переменных принимает вид

( ) ( )

H h t e dt











( ) ( )

h t H e d









2.10. РЯД ФУРЬЕ И ИНТЕГРАЛ ФУРЬЕ

Как было показано выше, гармонические функции

2j ft



иг-

рают исключительно важную роль в анализе цепей, как собствен-

ные функции любого линейного стационарного оператора. Благо-

даря этому среди всех базисов пространств сигналов, применяемых

в теории и практике, базис Фурье получил наибольшее распро-

странение и заслуживает более детального изучения.

2.10.1. РЯД ФУРЬЕ, ЕГО ФОРМЫ, СВОЙСТВА СПЕКТРОВ

Для пространства сигналов конечной длительности и огра-

ниченной энергии

()LT

ортонормальный базис

j kt













,k   

является полным, следовательно, всякий сигнал

( ) ( )x t L T

можно на интервале

 

/ 2, / 2TT

представить обоб-

щенным рядом Фурье по ортонормальным функциям

()

j kt

x t e









(2.38)

или рядом Фурье по ортогональным функциям

()

j kt

x t C e









. (2.39)

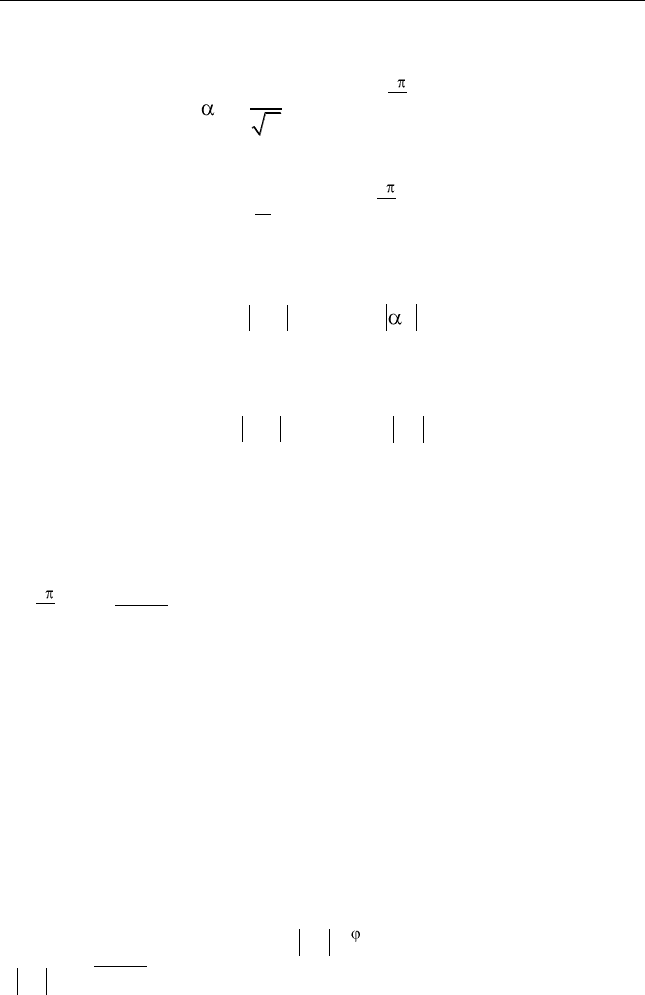
2. ОСНОВЫ ТЕОРИИ СИГНАЛОВ

Спектральные коэффициенты для этих рядов определяются выра-

жениями

()

j kt

x t e dt







(2.40)

()

j kt

C x t e dt







. (2.41)

Для ряда (2.38) справедливо равенство Парсеваля

()

x t dt













Для ряда (2.39) выполняется равенство

()

x t dt T C













До сих пор базисные функции рассматривались на конечном

временнóм интервале

 

/ 2, / 2TT

. Нетрудно видеть, что эти

функции могут рассматриваться и вне этого интервала, т.е. на всей

бесконечной временнóй оси. Поскольку все функции

 

j kt

ek  

периодичны, причем для их периодов величина

– наименьшее общее кратное, ряды (2.38) и (2.39), рассматри-

ваемые на всей временнóй оси, определяют периодическую функ-

цию, которая представляет собой сигнал

()xt

, повторяющийся с

периодом

Таким образом, ряд Фурье одинаково пригоден для представ-

ления сигналов конечной длительности и периодических сигналов.

Коэффициенты в обоих случаях находятся по формулам (2.40) или

(2.41). Далее будет рассматриваться комплексный ряд Фурье в

форме (2.39).

Коэффициенты ряда Фурье (2.39) даже для вещественного сиг-

нала в общем случае являются комплексными. Для удобства гра-

фического представления рассматривают отдельно модули и аргу-

менты коэффициентов

C C e

, при этом совокупность

 

Ck  

называется амплитудным спектром, а

2.10. Ряд Фурье и интеграл Фурье

 

  

– фазовым спектром сигнала. Для наглядности

амплитудный и фазовый спектр изображают решетчатыми спек-

тральными диаграммами, на которых соответствующие величины

показаны длинами отрезков, а сами эти отрезки размещены на час-

тотной оси с шагом, равным в выбранном масштабе частоте повто-

рения сигнала

1FT

(рис. 2.22).

–1

–2

–3

–4

2 F 3F 4F

–F–F2

–F3

–F4

F 3F 4F2 F

–F–F2

–F3

–F4

–1

–2

–3

–4

а б

Рис. 2.22. Амплитудная и фазовая спектральные диаграммы веще-

ственного сигнала

Если сигнал

()xt

принимает вещественные значения, ампли-

тудный спектр обладает свойством четности, а фазовый – свойст-

вом нечетности. Действительно, для произвольного спектрального

коэффициента

()

j kt

C x t e dt







с учетом вещественности сигнала

*( ) ( )x t x t

/ 2 / 2

( ) ( )

j kt j kt

C x t e dt x t e dt C







  







Таким образом, коэффициенты комплексного ряда Фурье ве-

щественного сигнала попарно комплексно сопряжены. Пользуясь

этим свойством, для вещественных сигналов можно получить дру-

гую форму ряда Фурье, также находящую применение.

Просуммируем пару базисных функций с номерами (индексами)

()k

с учетом соответствующих спектральных коэффициентов:

2 2 2 2

j kt j kt j kt j kt

T T T T

k k k k

C e C e C e C e





   

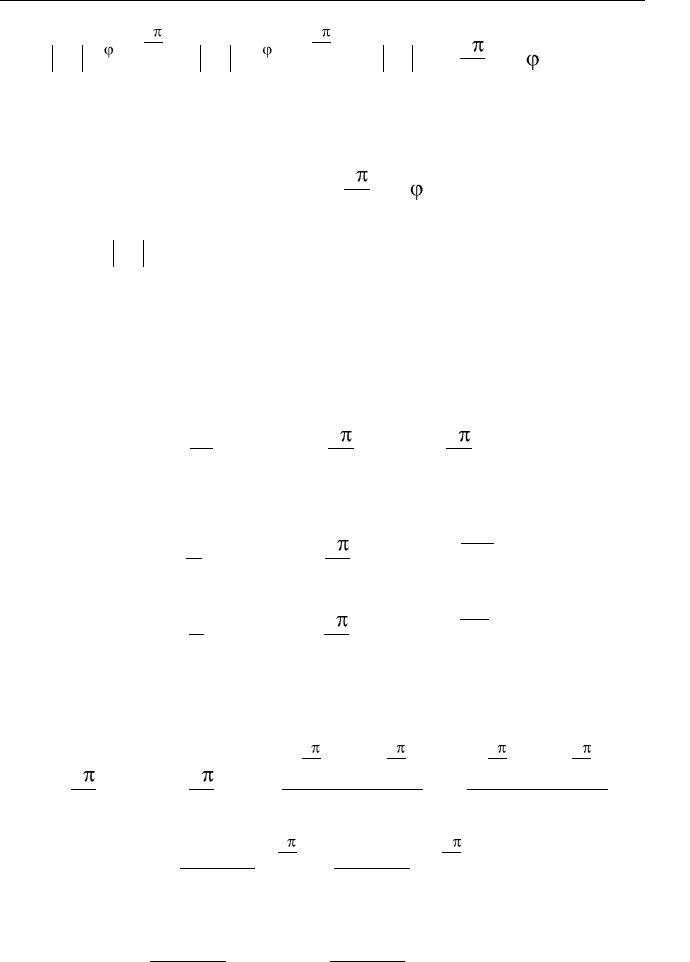
2. ОСНОВЫ ТЕОРИИ СИГНАЛОВ

2 cos

j kt j kt

k k k k

C e e C e e C kt





   





. (2.42)

Тогда ряд Фурье (2.39) можно записать в тригонометрической

форме

( ) cos

x t A kt















, (2.43)

где

2 , 0,

, 0;

















все коэффициенты

вещественны.

Ещѐ одна форма ряда Фурье для вещественных сигналов осно-

вана на разложении по тригонометрическим функциям, образую-

щим ортогональный базис

( ) cos sin

x t a kt b kt







  







со спектральными коэффициентами

( )cos , 0,

a x t kt dt k





  







( )sin , 1,

b x t kt dt k





  







Сложим с учетом коэффициентов две функции этого базиса,

имеющие одинаковую частоту, и воспользуемся формулой Эйлера:

2 2 2 2

cos sin

j kt j kt j kt j kt

T T T T

k k k k

e e e e

a kt b kt a b

T T j





   

j kt j kt

k k k k

a jb a jb







Сравнивая полученное выражение с выражениями (2.42), ви-

дим, что

a jb





, а

a jb







, откуда следуют связи

2.10. Ряд Фурье и интеграл Фурье

между спектральными коэффициентами для различных форм ряда

Фурье:





C 

k k k

A a b

A 

arctg



Очевидно, если сигнал представляет собой четную функцию, то

все синусоидальные компоненты ряда равны 0; аналогично, все

косинусоидальные компоненты равны нулю, если сигнал – нечет-

ная функция (при этом равна нулю и постоянная составляющая).

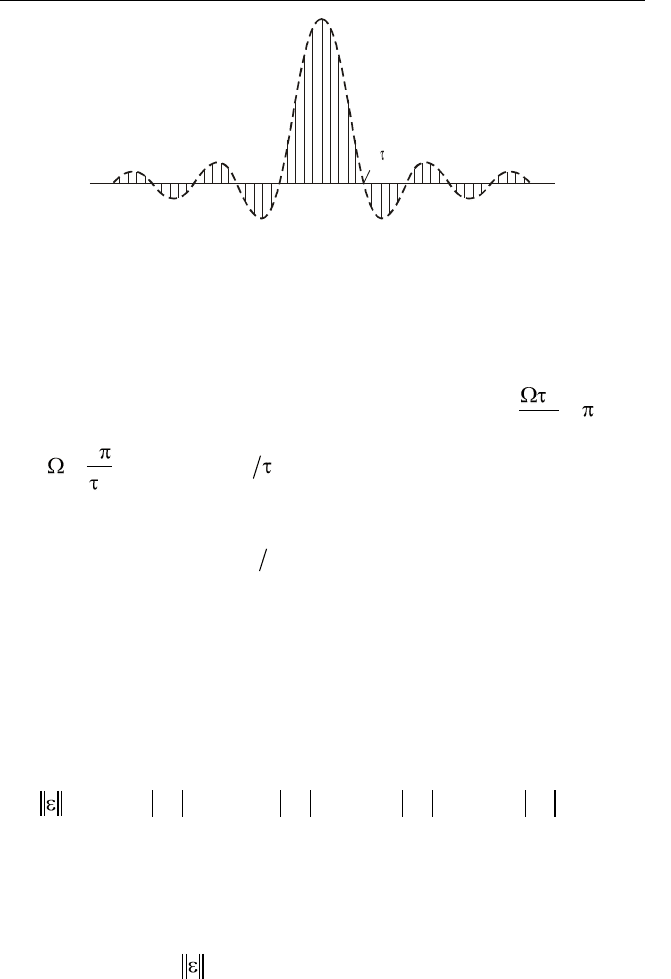
Пример 2.19. Периодическая с периодом

последователь-

ность прямоугольных импульсов амплитуды

и длительности

показана на рис. 2.23.

Спектральные коэффициенты комплексного ряда Фурье нахо-

дятся как

/ 2 / 2

1 1 2

( ) cos

j kt

C x t e dt U kt dt

T T T







  







ии

sin / 2

где введено обозначение круговой частоты

2 F



. Таким

образом, диаграмма амплитудного спектра сигнала, показанная на

рис. 2.24, имеет огибающую в форме известной функции вида

sin x

. Заметим, что все коэффициенты

оказались веществен-

ными, так что фазовый спектр равен нулю для всех

. Значение

постоянной составляющей сигнала

C U q



, где

qT

–

параметр импульсной последовательности, называемый скважно-

стью.

ut( )

–2Т –Т Т 2Т

Рис. 2.23. Периодическая последовательность

прямоугольных импульсов

2. ОСНОВЫ ТЕОРИИ СИГНАЛОВ

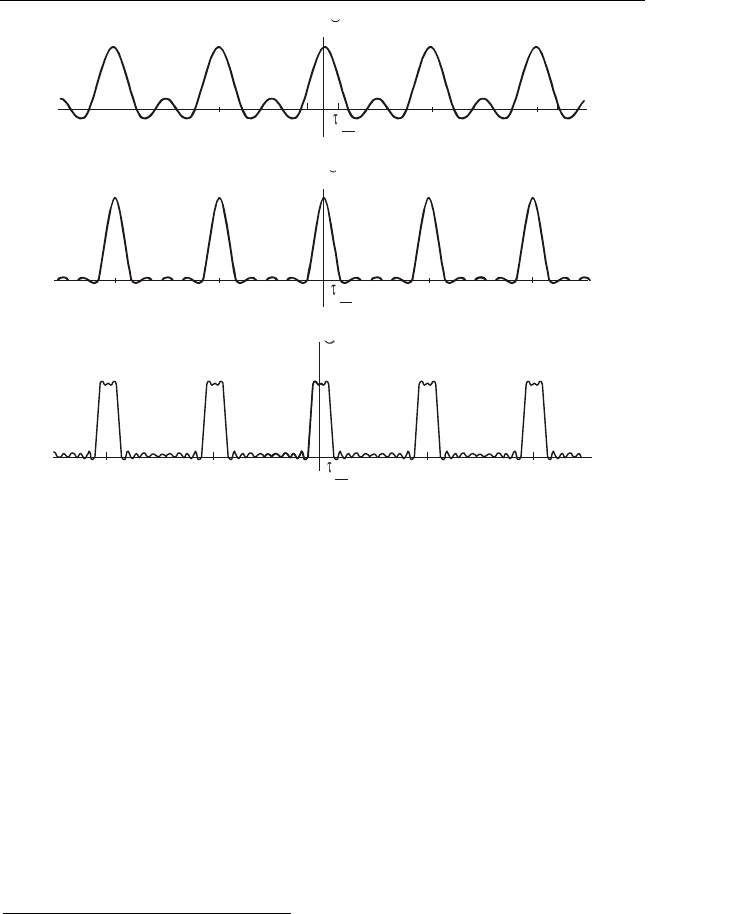
Рис. 2.24. Спектр периодической последовательности

прямоугольных импульсов

Последовательности прямоугольных импульсов широко при-

меняются в радиотехнике и связи в качестве моделей реальных

сигналов, поэтому спектр данного сигнала достоин более внима-

тельного рассмотрения. Прежде всего, обратим внимание, что оги-

бающая спектра впервые пересекает ось частот при



, т.е.

при



или при

1f 

. Таким образом, численное значение

скважности прямоугольной импульсной последовательности пока-

зывает, во сколько раз полуширина главного лепестка огибающей

спектра больше шага

1FT

следования по оси частот спектраль-

ных составляющих.

Конечная сумма ряда Фурье может служить аппроксимацией

сигнала. На рис. 2.25 показаны конечные суммы комплексного ря-

да Фурье периодической последовательности прямоугольных им-

пульсов при числе слагаемых 5, 11 и 25. Видно, что аппроксимация

становится точнее с ростом количества слагаемых. Ошибка ап-

проксимации при удержании в сумме

21N 

слагаемых (от

N

-го

до

-го) может быть найдена на основе равенства Парсеваля как

2 2 2 2

k k k k

k k N k k N

T C T C T C T C

   

    

   

   

. ◄

При увеличении числа слагаемых ряда Фурье ошибка аппрок-

симации периодического сигнала стремится к нулю по норме про-

странства

()LT

, т.е.

 

( ) ( ) 0

x t x t dt





  



. (2.44)

2.10. Ряд Фурье и интеграл Фурье

xt()

–2Т –Т Т 2Т

xt()

–2Т –Т Т 2Т

xt()

Рис. 2.25. Аппроксимация периодической последовательности,

показанной на рис. 2.23, суммой 5, 11 и 25 членов ряда Фурье

Здесь

()xt



– аппроксимация сигнала

()xt

. При этом максимальное

значение разности стремится не к нулю, а к конечной величине

(порядка 9 % от амплитуды импульса). Это явление известно как

явление Гиббса

. Причиной явления Гиббса является неравномер-

ная сходимость

ряда Фурье для разрывных функций. При равно-

мерной сходимости предел последовательности непрерывных

функций, каковыми являются конечные суммы ряда Фурье, сам

должен быть непрерывной функцией; в рассматриваемом же при-

мере пределом является разрывная (скачкообразная) функция.

В некоторых практических задачах таких, как синтез цифровых

фильтров, явление Гиббса нежелательно; существуют методы

уменьшения гиббсовских пульсаций (осцилляций), основанные на

коррекции коэффициентов ряда Фурье [5].

Джосайя Уиллард Гиббс (1839–1903) – выдающийся американский физик, один

из основателей статистической физики.

Сходимость, описываемая выражением (2.44), называется среднеквадратиче-

ской.

2. ОСНОВЫ ТЕОРИИ СИГНАЛОВ

2.10.2. СВОЙСТВА ПРЕОБРАЗОВАНИЯ ФУРЬЕ

Ряд Фурье представляет собой удобный инструмент анали-

за сигналов, заданных на конечном временном интервале, а также

периодических колебаний, так как позволяет заменить несчетное

множество (континуум) значений аналогового сигнала счетным

множеством спектральных коэффициентов. Базис Фурье

 

j kt

ek  

полон в пространстве

()LT

, поэтому любой

сигнал из

()LT

можно сколь угодно точно аппроксимировать ко-

нечной суммой ряда Фурье, выбрав достаточно большое число сла-

гаемых. Среди всех полных в

()LT

базисов базис Фурье имеет то

преимущество, что он составлен из функций, собственных для лю-

бого ЛИС-оператора. Это максимально упрощает анализ воздейст-

вия периодических сигналов на ЛИС-цепи.

Для пространства

( , )L   

сигналов ограниченной энергии,

заданных на всей временной оси, базис

 

j kt

ek  

не явля-

ется полным ни при каком

и, следовательно, непригоден для

представления сигналов, так как ошибку аппроксимации нельзя в

общем случае сделать произвольно малой путем учета достаточно-

го числа слагаемых ряда Фурье. В самом деле, если сигнал имеет

бесконечную длительность и конечную энергию, т.е. принадлежит

пространству

( , )L  

, то он должен убывать при стремлении

t  

, и притом достаточно быстро. При любом выборе

ряд

Фурье для такого сигнала определяет периодическую функцию,

которая может совпадать с заданным сигналом только на интерва-

ле длительности

, а за его пределами неизбежно будет отличать-

ся от него. Более того, периодическая функция всегда имеет беско-

нечную энергию, поэтому и ошибка аппроксимации при любом

будет иметь бесконечную норму. Это и означает неполноту счет-

ного базиса Фурье в

( , )L  

. Итак, единственным способом

использовать комплексные экспоненты в качестве базисных функ-

Напомним, что в

( , )L

существуют полные ортонормальные счетные

базисы (например, базис, составленный из функций Эрмита [3]), но они, к со-

жалению, не являются собственными для ЛИС-цепей.