Васюков В.Н. Теория электрической связи
Подождите немного. Документ загружается.


2.5. Гильбертово пространство
43
Действительно, пусть вектор
x
представлен рядом (2.12). Его
норма
*
2
, , ,
k k m m k m k m
k m k m
x x x u u u u
2
*
k m km m
k m m
. (2.13)
Таким образом, доказано равенство Парсеваля. В пространст-
вах
2
L
и
2
l
равенство Парсеваля для сигналов, заданных спектра-
ми
,,
m
m
и
,,
m
m
относительно полных орто-
нормальных базисов, принимает соответственно вид
2
2
| ( ) |
m
m
x t dt
и
2
2
[]
m
nm
xn
.
Пусть два вектора представлены в некотором полном ортонор-
мальном базисе выражениями
kk
k
xu
и
kk
k
yu
. Тогда
их скалярное произведение
( , ) ,
k k m m
km
x y u u
**
k m km m m
k m m
. (2.14)
Это выражение носит название обобщенной формулы Рэлея. Зна-
чение этих равенств состоит в возможности оперировать вместо
сигналов коэффициентами их представления в полных ортонор-
мальных базисах (спектрами), даже не интересуясь конкретным
видом базиса.
Обобщенный ряд Фурье (ОРФ), представляющий сигнал из
бесконечномерного пространства
L
, содержит в общем случае
бесконечно много слагаемых. Часто на практике приходится рас-
сматривать усеченный ряд, сумма
x
которого аппроксимирует
данный сигнал
x
:
1
K
kk
k
x x u
.

2. ОСНОВЫ ТЕОРИИ СИГНАЛОВ
44
Усеченный ОРФ представляет сиг-
нал в виде линейной комбинации
K
базисных векторов, поэтому
x
принад-
лежит
K
-мерному подпространству
K
L
пространства
L
. Поскольку все ба-
зисные векторы взаимно ортогональны,
ошибка аппроксимации
xx
орто-
гональна по отношению к
K
L
и при-
надлежит ортогональному дополнению
L
, такому, что
K
L L L
(рис. 2.9).
Символ
обозначает прямую сумму
пространств (например, трехмерное евклидово пространство мож-
но представить прямой суммой плоскости и прямой, ортогональ-
ной этой плоскости). Очевидно,
2
2 2 2 2
2
2 2 2 2
11
2
| | 0
KK
k k k
kk
x x x u x
,
откуда следует неравенство Бесселя
2
2
2
1
||
K
k
k
x
, (2.15)
которое означает, что при аппроксимации сигнала конечной сум-
мой обобщенного ряда Фурье энергия аппроксимирующего сигна-
ла не может превзойти энергию аппроксимируемого сигнала. Ра-
венство возможно только в том случае, если сам сигнал
принадлежит подпространству
K
L
.
С увеличением размерности подпространства
K
L
, т.е. с увели-
чением числа слагаемых, входящих в конечную сумму обобщенно-
го ряда Фурье, норма ошибки стремится к нулю (в этом и состоит
практический смысл требования полноты базиса). Таким образом,
располагая полным ортонормальным базисом, можно обеспечить
сколь угодно точную аппроксимацию сигнала суммой конечного
числа наперед заданных функций с соответствующими весовыми
коэффициентами; при этом гарантируется, что при заданном числе
слагаемых ошибка аппроксимации будет минимальной.
Пример 2.10. Прямоугольный импульс длительности
и
и ам-
плитуды
A
, изображенный на рис. 2.10, на интервале
( / 2, / 2)TT
,
x
L
K
x
Рис. 2.9. Конечномерная
аппроксимация сигнала

2.5. Гильбертово пространство
45
ut( )
A
/2
t
и
– /2
и
k
2A
и
Т
0
Рис. 2.10. Прямо-
угольный видеоим-
пульс
Рис. 2.11. Спектральная диа-
грамма прямоугольного им-
пульса, заданного на конечном
временнóм интервале
и
,T
можно представить рядом (2.9) с коэффициентами, най-
денными согласно выражению
и
и
2
/2
и
и
и
/2
sin /
2
1
/
j kt
T
k
kT
A
Ae dt
kT
TT
.
Диаграмма, отображающая спектр прямоугольного импульса
относительно ортонормального базиса Фурье, приведена на
рис. 2.11. Аппроксимации прямоугольного импульса, полученные
как конечные суммы
2
1
()
K
j kt
T
k
kK
x t e
T
при
5K
,
10K
и
20,K
показаны различными линиями на рис. 2.12. ◄
ut()
t
Рис. 2.12. Аппроксимации прямоугольного
импульса конечными суммами ряда Фурье
Пример 2.11. Базис, составленный из функций Уолша, является
ортонормальным полным базисом для
2
( 1/ 2,1/ 2)L
. Графики че-
тырѐх первых функций Уолша относительно нормированного вре-
мени
/tT
показаны на рис. 2.13. Функции Уолша привлекли
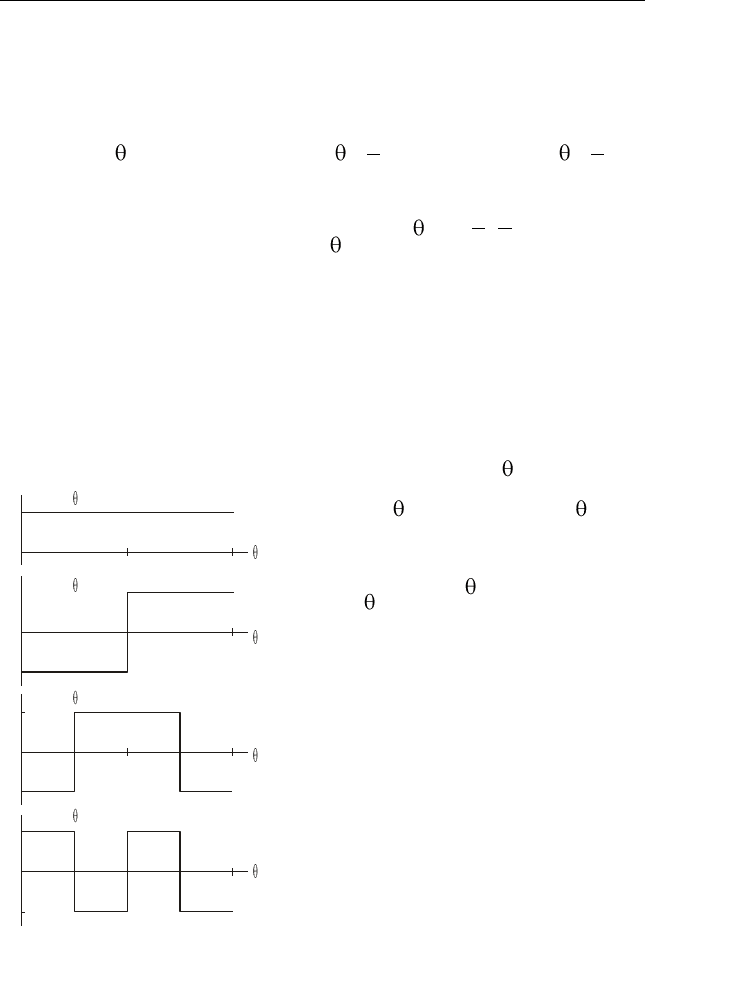
2. ОСНОВЫ ТЕОРИИ СИГНАЛОВ
46
внимание благодаря простоте их генерирования при помощи пере-
ключательных схем.
Функции Уолша определяются с помощью рекуррентного со-
отношения
/2
11
wal 2 , ( 1) wal , 2 ( 1) wal , 2
22
np
np
n p n n
,
0,1, 2,...n
,
0,1;p
11
1, , ,
wal 0,
22
0 в противном случае.
Здесь
/2n
обозначает целую часть числа
/2n
.
Иногда используют систему функций Уолша, заданную на ин-
тервале нормированного времени
(0;1)
. Эта система составляет
полный ортонормальный базис для пространства
2
(0,1)L
; такие
функции Уолша определяются рекуррентными соотношениями
wal 2 ,
wal , 2 ( 1) wal , 2 1 ,
np
np
nn
0,1, 2,...n
,
0,1;p
1, 0,1 ,
wal 0,
0 в противном случае.
Известны также способы опреде-
ления функций Уолша через матри-
цы Адамара; при этом получаемые
системы функций отличаются нуме-
рацией (способом упорядочения);
подробнее см., например, [23]. ◄
Разложение сигналов в различ-
ных ортонормальных или орто-
гональных базисах применяется на
практике в тех случаях, когда опери-
ровать спектром сигнала удобнее,
чем его временнóй функцией. Уст-
ройство, вычисляющее спектральные
коэффициенты сигнала, называется
анализатором спектра (рис. 2.14).
1
1
1
1
1
1
1
wal(0, )
wal(1, )
wal(2, )
–1/2 0 1/2
wal( , )3
–1/2 0 1/2
–1/2 0 1/21/4–1/4
–1/2 0 1/21/4–1/4
Рис. 2.13. Функции Уолша
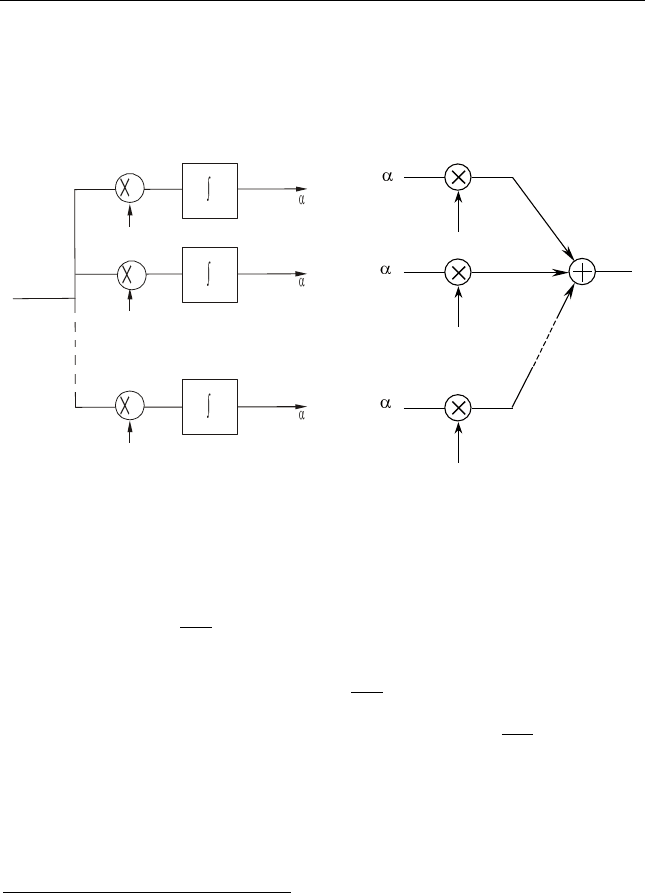
2.5. Гильбертово пространство
47
Зная спектральные коэффициенты и базисные функции, можно
восстановить сигнал, т.е. выполнить его синтез согласно рис. 2.15.
Разложение сигналов относительно неортогонального базиса также
возможно, но оно сложнее и его результаты труднее интерпрети-
ровать.
u*
1
u*
2
u*
K
xt()
2
1
K
()xt
1
()ut
2
()ut
()
K
ut
1
2
K
Рис. 2.14. Структура анализатора
спектра
Рис. 2.15. Синтез сигнала
по его спектру
Существует алгоритм, называемый процедурой Грама –
Шмидта
22
, позволяющий по имеющемуся набору линейно незави-
симых функций (векторов) построить ортонормальный базис.
Пусть
, 1,
k
vk
– совокупность линейно независимых век-
торов, на основе которой требуется построить ортонормальный
базис. Введем обозначение
, 1,
k
wk
для вспомогательной со-
вокупности векторов, а также обозначение
, 1,
k
uk
для орто-
нормального базиса, который получается в результате выполнения
следующих шагов:
1) первый вспомогательный вектор приравнивается первому
вектору исходного линейно независимого базиса
11
wv
; первый
22
Йорген Грам (1850 – 1916) – датский математик, известен исследованиями в
области математической статистики, теории чисел, теории приближения функ-
ций рядами; Эрхард Шмидт (1876 – 1959) – немецкий математик, известен ре-
зультатами исследований в области интегральных уравнений и функциональ-
ного анализа.

2. ОСНОВЫ ТЕОРИИ СИГНАЛОВ
48
вектор результирующего ортонормального базиса получается нор-
мировкой
11
1
2
1
uw
w
;
2) второй вспомогательный вектор
2
w
получается вычитанием
из второго вектора
2
v
исходной совокупности его проекции на уже
построенный вектор
1
u
ортонормального базиса, после чего произ-
водится его нормировка и получается второй вектор ортонормаль-
ного базиса
2 2 2 1 1
( , )w v v u u
,
22
2
2
1
uw
w
;
3) третий вспомогательный вектор
3
w
формируется путем вы-
читания из очередного вектора
3
v
исходной совокупности его про-
екций на уже построенные векторы
1
u
и
2
u
ортонормального ба-
зиса, после чего этот вектор нормируется
3 3 3 1 1 3 2 2
( , ) ( , )w v v u u v u u
,
33
3
2
1
uw
w
и т.д.
Продолжая процедуру Грама – Шмидта, можно построить ор-
тонормальный базис любой размерности.
Пример 2.12. Множество
23
4 0 1 2 3
{ ( ) 1, ( ) , ( ) , ( ) },S v t v t t v t t v t t
где
1,1t
, линейно независимо (см. пример 2.1). В результате
u
1
2
0
3
u
u u
–1 –0,5
0
0,5 1
t
–1
2
–2
1
Рис. 2.16. Базис, полученный при-
менением процедуры Грама–Шмидта
к совокупности степенных функ-
ций, показанной на рис. 2.7

2.6. Непрерывные представления сигналов
49
применения процедуры Грама – Шмидта получается ортонормаль-
ный базис, состоящий из четырех функций, показанных на
рис. 2.16. Это известные полиномы Лежандра, нормированные к
единице по норме пространства
2
( 1,1)L
. ◄
Очевидно, в пространствах аналоговых и дискретных сигналов
можно построить бесконечно много ортонормальных базисов. Вы-
бор наиболее подходящего базиса определяется конкретной ре-
шаемой задачей.
2.6. НЕПРЕРЫВНЫЕ ПРЕДСТАВЛЕНИЯ
СИГНАЛОВ
Обобщенный ряд Фурье представляет сигнал в виде взвешен-
ной суммы счетного
23
множества базисных функций. Иногда счет-
ный базис неудобен или не годится для описания сигнала. Напри-
мер, счетный базис Фурье, полный в
2
()LT
, не полон в
2
( , )L
и поэтому непригоден для представления сигналов бесконечной
длительности. С другой стороны, известные полные в
2
( , )L
счетные базисы не обладают теми привлекательными свойствами,
которые обусловили широкое применение базиса Фурье в теории и
практике и о которых далее будет сказано подробно (см. разд. 2.9).
Гармонические функции, аналогичные функциям базиса Фурье,
могут применяться для представления сигналов из
2
( , )L
, но
для этого мощность их множества должна быть больше мощности
счетного множества (иначе говоря, множество должно быть не-
прерывным).
Таким образом, понятие обобщенного ряда Фурье подвергается
дальнейшему обобщению. Суть этого обобщения заключается в
замене суммы бесконечного счетного множества базисных функ-
ций, умноженных на спектральные коэффициенты, интегралом от
функции двух переменных (которая представляет собой «несчет-
ное множество» базисных функций), умноженной на функцию од-
ной переменной, называемой спектральной плотностью.
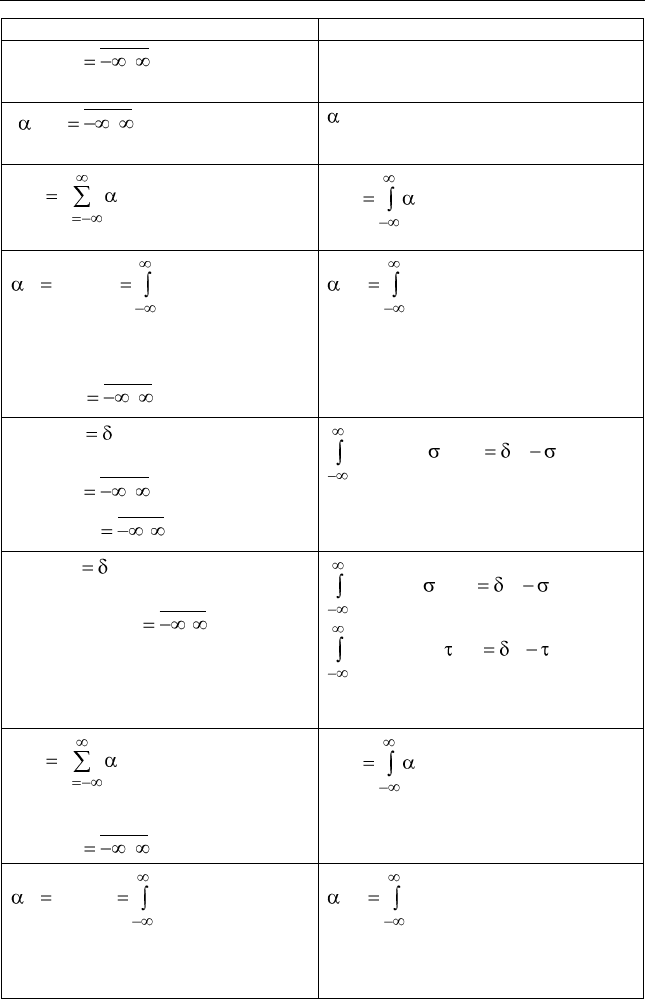
Ниже приведены попарно термины и формулы, соответствую-
щие дискретному и непрерывному (интегральному) представлени-
ям аналоговых сигналов.
23
Элементы счетного множества могут быть пронумерованы, т.е. поставлены в
соответствие элементам множества целых неотрицательных чисел.
2. ОСНОВЫ ТЕОРИИ СИГНАЛОВ
50
Дискретное представление
Интегральное представление
( ), ,
k
v t k
– базис (необя-
зательно ортогональный)
( , )v s t
– базисное ядро интеграль-
ного представления
,,
k
k
– спектр сигнала
относительно выбранного базиса
()s
– спектральная плотность сиг-
нала относительно выбранного ядра
( ) ( )
kk
k
x t v t
– дискретное
представление сигнала
( ) ( ) ( , )x t s v s t ds
– интеграль-
ное представление сигнала
*
, ( ) ( )
k k k
x w x t w t dt
–
формула нахождения спектрально-
го коэффициента с использованием
сопряженного (взаимного) базиса
( ), ,
k
w t k
*
( ) ( ) ( , )s x t w s t dt
– (2.16)
формула нахождения спектральной
плотности с использованием сопря-
женного ядра
( , )w s t
,
k m km
vw
– условие взаимно-
сти (сопряженности) базисов
( ), ,
k
v t k
и
( ), ,
k
w t k
*
( , ) ( , ) ( )v s t w t dt s
– (2.17)
условие сопряженности ядер
( , )v s t
и
( , )w s t
,
k m km
uu
– условие ортонор-
мальности (самосопряженности)
базиса
( ), ,
k
u t k
*
( , ) ( , ) ( )u s t u t dt s
и
*
( , ) ( , ) ( )u s t u s ds t
– усло-
вия самосопряженности базисного
ядра
( , )u s t
( ) ( )
kk
k
x t u t
– обобщенный
ряд Фурье (представление сигна-
ла в ортонормальном базисе
{ ( ), , })
k
u t k
( ) ( ) ( , )x t s u s t ds
– интеграль-
ное представление сигнала относи-
тельно самосопряженного базисно-
го ядра
( , )u s t
*
, ( ) ( )
k k k
x u x t u t dt
–
формула нахождения спектрально-
го коэффициента относительно
ортонормального базиса
*
( ) ( ) ( , )s x t u s t dt
– формула
нахождения спектральной плотно-
сти относительно самосопряженно-
го ядра
( , )u s t

2.6. Непрерывные представления сигналов
51
Таким образом, интегральное представление имеет много об-
щего с обобщенным рядом Фурье.
Пример 2.13. Для представления сигналов из пространства
2
( , )L
очень часто используется базисное ядро
2
( , )
j ft
u f t e
(вместо переменной
s
в обозначении ядра исполь-
зовано общеупотребительное обозначение частоты буквой
f
). Яд-
ро является самосопряженным, так как
* 2 2
( , ) ( , )
j ft j t
u f t u t dt e e dt
2 ( )
sin2 ( )
lim lim ( )
()
T
j f t
TT
T
Tf
e dt f
f
(аналогично доказывается и второе условие самосопряженности).
Поэтому спектральная плотность сигнала
()xt
относительно
данного ядра, которую обозначим
()Xf
, определяется выражением
2
( ) ( )
j ft
X f x t e dt
, (2.18)
известным как преобразование Фурье; формула интегрального
представления сигнала
2
( ) ( )
j ft
x t X f e df
(2.19)
называется обратным преобразованием Фурье. ◄
Запишем скалярное произведение двух сигналов
()xt
и
()yt
,
выразив сигналы через спектральные плотности при помощи об-
ратного преобразования Фурье:
* 2 * 2
( , ) ( ) ( ) ( ) ( )
j t j ft
x y x t y t dt X e d Y f e df dt
* 2 ( )
( ) ( )
j f t
X Y f e dtdfd
**
( ) ( ) ( ) ( ) ( )X Y f f dfd X f Y f df
.

2. ОСНОВЫ ТЕОРИИ СИГНАЛОВ
52
Таким образом, получена обобщенная формула Рэлея
**
( ) ( ) ( ) ( )x t y t dt X f Y f df
(2.20)
для интегрального представления сигналов относительно базисно-
го ядра Фурье
2j ft
e
. Аналогичное выражение будет справедливо
для интегрального представления сигналов относительно любого
самосопряженного ядра.
Подставляя в (2.20)
( ) ( )y t x t
, получаем равенство Парсеваля
22
| ( ) | | ( ) |x t dt X f df
. (2.21)
Симметричная форма левых и правых частей выражений (2.20)
и (2.21) должна наводить на мысль, что «естественное» временнóе
представление сигнала есть на самом деле представление относи-
тельно некоторого самосопряженного ядра. Справедливость такого
утверждения устанавливается в следующем примере.
Пример 2.14. Для пространства сигналов
2
( , )L
примем в
качестве базисного ядра сдвинутую (задержанную) -функцию
( , ) ( )u t t
(вместо переменной
s
использовано обозначение
задержки буквой ). Это ядро является самосопряженным [2]. По-
этому спектральная плотность сигнала
()xt
относительно данного
ядра определяется выражением
( ) ( ) ( )x x t t dt
, (2.22)
а интегральное представление сигнала задается формулой
( ) ( ) ( )x t x t d
. (2.23)
Полученное выражение, описывающее стробирующее свойство
-функции и совпадающее с динамическим представлением сиг-
нала (2.4), явно демонстрирует тот факт, что обычное временнóе
представление сигнала можно рассматривать как интегральное
(спектральное) представление относительно базисного ядра
( , ) ( )u t t
со спектральной плотностью
()x
. Иными слова-
ми, временная функция
()x
, описывающая сигнал, есть не что
