Васюков В.Н. Теория электрической связи

Подождите немного. Документ загружается.

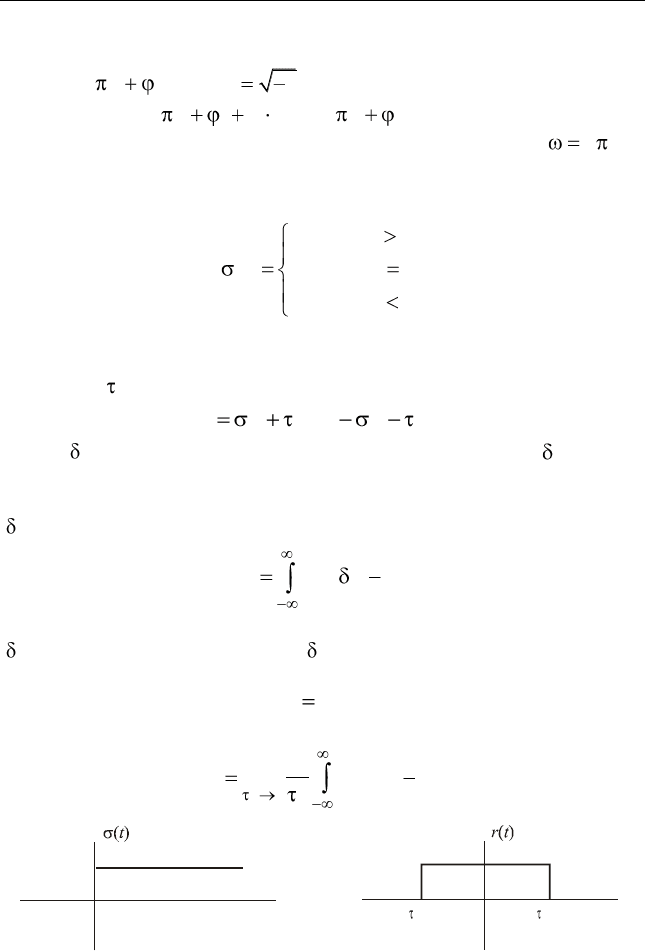
2.1. Сигналы и их математические модели

часто используют косинус. Кроме того, во многих случаях рас-

сматривается комплексное гармоническое колебание

exp (2 )A j ft

, где

. Это колебание можно представить

суммой

cos(2 )A ft

sin(2 )j A ft

. Иногда в описаниях

гармонических колебаний используют круговую частоту

2 f

Б) Функция включения Хевисайда (рис. 2.1, а), определяемая

выражением

1 при 0,

( ) 0,5 при 0,

0 при 0.

(2.1)

Функцию Хевисайда, в частности, удобно использовать для пред-

ставления прямоугольного импульса единичной амплитуды и дли-

тельности

(рис. 2.1, б):

ии

( ) ( /2) ( /2)r t t t

В) -функция Дирака (читается «дельта-функция»)

()t

, кото-

рая на самом деле является обобщенной функцией, т.е., строго

говоря, не функцией в обычном смысле слова [1]. Определяется

-функция выражением

( ) ( ) ( )f t f t t t dt

, (2.2)

которое известно как стробирующее (фильтрующее) свойство

-функции. Оно означает, что -функция, входящая в произведе-

ние под знаком интеграла, выделяет бесконечно узкий «срез» (от-

счѐт) функции

()ft

в точке

. Выражение (2.2) можно пони-

мать как предел

( ) lim ( ) ( )f t f t r t t dt

– /2

а б

Рис. 2.1. Функция Хевисайда (а) и прямоугольный импульс (б)

2. ОСНОВЫ ТЕОРИИ СИГНАЛОВ

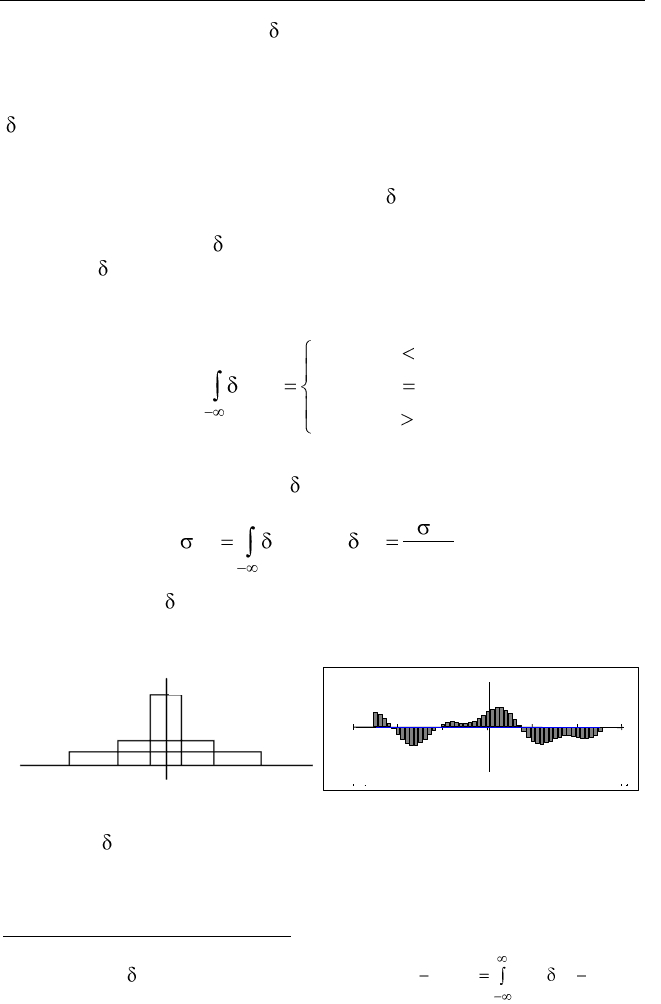
С такой точки зрения -функцию можно рассматривать как

предел последовательности все более коротких прямоугольных

импульсов со все большей амплитудой, так что площадь всех

импульсов одинакова и равна 1. Тогда (нестрого) можно считать

-функцию «импульсом» нулевой длительности и бесконечной

амплитуды с единичной площадью (рис. 2.2, а). Не следует, одна-

ко, забывать, что это не обычная, а обобщенная функция, которая

имеет особые свойства: так, например, -функцию можно диффе-

ренцировать

, но нельзя возводить в квадрат. Поэтому, например,

выражение «энергия -функции» не имеет смысла. Нужно отме-

тить, что -функция играет в теории сигналов совершенно исклю-

чительную роль, и в дальнейшем часто будет использоваться.

Очевидно, что интеграл

0 при 0,

( ) 0,5 при 0,

1 при 0.

t dt t

Сопоставляя это выражение с формулой (2.1), легко видеть, что

функция Хевисайда связана с -функцией выражениями

( ) ( )

t t dt

;

()

; (2.3)

таким образом, -функцию можно формально использовать для

дифференцирования разрывных функций.

x(t)

а б

Рис. 2.2. -функция, как предел последовательности прямоугольных

импульсов (а) и представление аналогового сигнала «суммой

импульсов» (б)

Производная -функции определяется выражением

'( ) ( ) '( )f t f t t t dt

2.1. Сигналы и их математические модели

Выражение (2.2), переписанное для сигнала

()xt

с учетом чет-

ности -функции в виде

( ) ( ) ( )x t x t d

, (2.4)

можно представить, как предел

ии

()

( ) lim ( )

r t n

x t x n

описывающий сигнал «сплошной суммой бесконечно узких им-

пульсов» (рис. 2.2, б). Такое представление часто называют дина-

мическим. Для сигнала, удовлетворяющего условию

( ) 0xt

при

, возможна другая форма динамического представления, осно-

ванная на функции Хевисайда

()

( ) (0) ( ) ( )

x t x t t d

(2.5)

и получаемая предельным переходом при

, примененным к

выражению

( 1) ( )

( ) (0) ( ) ( )

x n t x n t

x t x t t n t t

где

– временной интервал.

Для представления дискретных сигналов используются функ-

ции целого аргумента

, обладающие свойствами, аналогичными

свойствам функций (А – В).

а) Гармонические последовательности

[ ] sin( )x n A n

[ ] cos( )x n A n

и комплексная экспоненциальная последова-

тельность

[ ] exp[ ( )]x n A j n

б) Ступенчатая последовательность (рис. 2.3, а), аналогичная

функции Хевисайда и определяемая выражением

1 при 0,

[]

0 при 0.

в) Функция дискретной переменной, называемая -последова-

тельностью и играющая в теории дискретных сигналов роль, ана-

2. ОСНОВЫ ТЕОРИИ СИГНАЛОВ

логичную роли -функции для аналоговых сигналов, определяется

выражением

1, 0,

[]

0, 0

и является вполне обычной функцией, которую можно представить

графиком (рис. 2.3, б).

0 n

а б

Рис. 2.3. Ступенчатая единичная последовательность (а)

и -последовательность (б)

Операция дифференцирования для функций дискретного аргу-

мента не имеет смысла и заменяется вычислением разности сосед-

них отсчетов, поэтому выражениям (2.3) соответствуют очевидные

соотношения

[ ] [ ]

u n k

[ ] [ ] [ 1]n u n u n

Дискретный сигнал

[]xn

можно описать выражени-

ем, аналогичным динамическому представлению аналогового сиг-

нала (2.4):

[ ] [ ] [ ]

x n x k n k

. (2.6)

Это очевидное выражение означает, что сигнал

[]xn

представля-

ется суммой сдвинутых -последовательностей при всевозможных

целых сдвигах

, при этом каждая -последовательность умножа-

ется на соответствующий амплитудный коэффициент, равный

[]xk

Используя функции (А – В) и (а – в) при различных значениях

параметров (амплитуд, частот и начальных фаз для гармонических

функций, а также амплитуд и временных сдвигов для остальных),

можно получить математические описания (модели) для очень ши-

рокого класса сигналов (континуальных и дискретных), фактиче-

ски для всех сигналов, применяемых на практике. Однако во мно-

гих случаях удобнее оказываются иные модели.

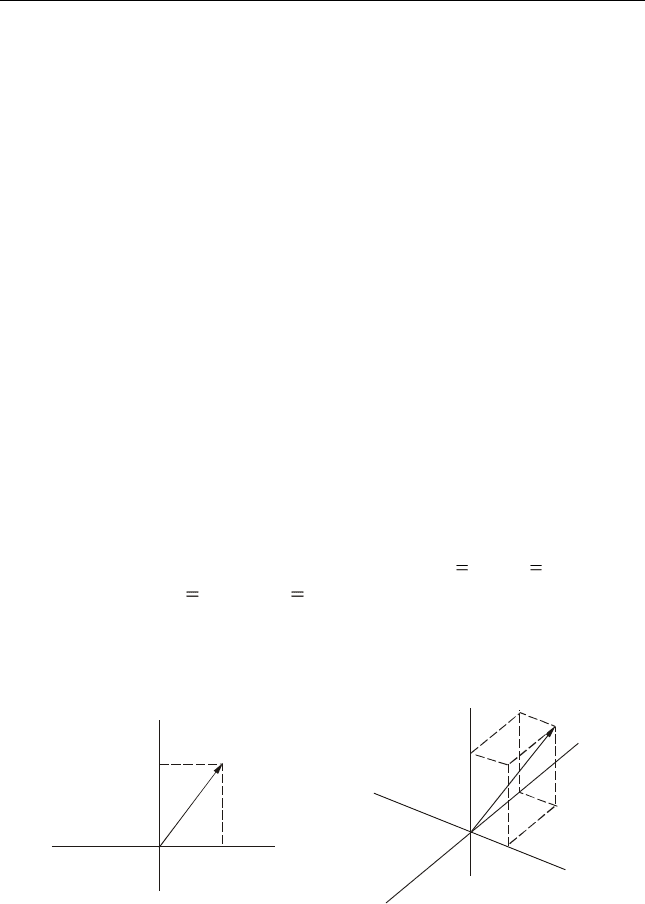
2.1. Сигналы и их математические модели

Представление сигнала (колебания) в виде графика описываю-

щей его функции является наглядным и привычным. В самом деле,

большинство сигналов описываются функциями времени, а одним

из наиболее распространенных приборов для измерения характе-

ристик электрических сигналов является осциллограф, отобра-

жающий именно временной график сигнала.

Временнóе представление не является, однако, ни единственным,

ни самым лучшим, и на практике при решении конкретных задач сле-

дует выбирать наиболее удобные формы описания сигналов.

Основное неудобство, связанное с временным представлением

сигналов, заключается в том, что сигналу соответствует сложный

объект (функция, изображаемая графиком) в простом пространстве

(на плоскости). В современной теории сигналов используется изо-

бражение сигнала простым объектом (точкой) в сложном простран-

стве [2]. Это пространство представляет собой множество всевоз-

можных сигналов, рассматриваемых в данной задаче, наделенное

соответствующими структурными свойствами. При этом свойства

сигналов получают наглядное геометрическое истолкование, а для

синтеза и анализа сигналов и систем их обработки применяется ап-

парат современной математики (функциональный анализ).

Основные идеи такого подхода проще изложить для дискретно-

го сигнала. Рассмотрим для примера множество дискретных сигна-

лов, таких, что все значения (отсчеты) этих сигналов равны нулю,

за исключением значений, соответствующих

. Прида-

вая значениям

[1]xx

[2]xx

сигнала

[]xn

смысл абсциссы и

ординаты точки (вектора) на плоскости, получаем представление

всего множества таких сигналов множеством векторов в двумер-

ном евклидовом пространстве (рис. 2.4, а). Множество сигналов,

x[2]

x[1]

x[2]

x[]3

а б

Рис. 2.4. Представление сигнала точкой (вектором) на плоскости (а)

и представление сигнала вектором в трехмерном пространстве (б)

2. ОСНОВЫ ТЕОРИИ СИГНАЛОВ

которые могут иметь три ненулевых отсчета (например, при

), представляется множеством векторов в трехмерном

пространстве (рис. 2.4, б).

Продолжая рассуждения, приходим к представлению множест-

ва всех сигналов, определяемых их значениями в конечном множе-

стве точек дискретной временнóй оси

1, 2,...,nN

множеством

векторов

-мерного евклидова пространства. Каждый такой век-

тор представляет собой упорядоченный набор чисел (координат),

равных значениям сигнала в соответствующие моменты времени.

Ясно, что такое представление является взаимно однозначным, а

следовательно, не приводит к потере информации.

Несмотря на то, что евклидово пространство размерности выше

трѐх обычный человек вообразить не в состоянии,

-мерное евкли-

дово пространство является весьма обычным и удобным инструмен-

том исследования, так как свойства евклидова пространства сохра-

няются при любой его размерности. Кроме того, в большинстве

случаев рассматриваются пары сигналов (векторов), а любые два

вектора лежат в общем для них двумерном подпространстве (плос-

кости). Таким образом, даже не очень богатого пространственного

воображения оказывается вполне достаточно для того, чтобы ориен-

тироваться в сигнальном пространстве любой размерности.

Устремляя

к бесконечности, получаем бесконечномерное

евклидово пространство, пригодное для представления всех дис-

кретных сигналов, определенных на бесконечной целочисленной

временнóй оси

. Это пространство имеет бесконечное,

но счетное множество «координатных осей». Каждому сигналу

взаимно однозначно соответствует бесконечный (счетный) упоря-

доченный набор координат вектора, равных, например, отсчетам

этого сигнала в соответствующие моменты времени.

Переходя к континуальным сигналам, получаем бесконечно-

мерное пространство с несчетным множеством (континуумом)

«координатных осей», при этом сигналу соответствует бесконеч-

ный несчетный упорядоченный «набор координат» вектора, рав-

ных (нестрого говоря) отсчетам этого сигнала в соответствующие

моменты времени, которые теперь следуют друг за другом «беско-

нечно плотно», т.е. непрерывно. Таким образом, и дискретные, и

аналоговые сигналы могут быть представлены векторами в линей-

ных пространствах соответствующих размерностей.

Чтобы использовать преимущества таких моделей, следует

вначале убедиться в том, что действиям над элементами линейного

пространства (векторами) соответствуют операции, применимые к

реальным сигналам.

2.2. Сигналы и действия над ними

2.2. СИГНАЛЫ И ДЕЙСТВИЯ НАД НИМИ

В каждой практической задаче, связанной с получением (ге-

нерированием), передачей, приемом и обработкой сигналов, рас-

сматриваются сигналы из определенного множества. Так, можно,

например, рассматривать множество

()MT

всех континуальных

сигналов, заданных на конечном временнóм интервале

[0, ]tT

(интервале наблюдения), или множество всех дискретных сигна-

лов, определенных на конечном участке дискретной временнóй оси

1,nN

. Сигналы из одного множества обладают некоторыми об-

щими свойствами, что и позволяет рассматривать множество как

целое.

На практике над сигналами выполняются некоторые действия

(операции), такие, например, как сложение (суммирование). Для

этого применяются устройства, называемые сумматорами. Кроме

того, суммирование выполняется естественным путем при распро-

странении различных сигналов в общем канале связи или в про-

странстве, и в этом случае гово-

рят о взаимных помехах. Сум-

мирование применимо к сигна-

лам, имеющим общую область

определения. Например, склады-

вая сигналы

()st

, опре-

деленные на конечном интервале

[0, ]T

, получаем сигнал

()st

определенный на этом же интер-

вале (сумма сигналов из множе-

ства

()MT

снова принадлежит

()MT

, рис. 2.5. В таких случаях

говорят, что множество замкну-

то относительно сложения.

Вторая операция, часто при-

меняемая на практике, – умно-

жение на некоторый постоянный

коэффициент. Множитель может

быть больше единицы, что соот-

ветствует усилению сигнала, или

меньше единицы, тогда имеет

место ослабление. Ослабление

может быть естественным

st ( )

Рис. 2.5. Сигнал (а), помеха (б)

и сумма сигнала и помехи (в)

2. ОСНОВЫ ТЕОРИИ СИГНАЛОВ

(вследствие затухания сигнала в линии передачи или рассеяния

энергии в пространстве) или преднамеренным, выполняемым, на-

пример, с помощью устройств, называемых аттенюаторами.

Усиление выполняется при помощи усилителей. Множитель может

быть и отрицательным, тогда меняется полярность сигнала, а соот-

ветствующее устройство называют инвертирующим усилителем,

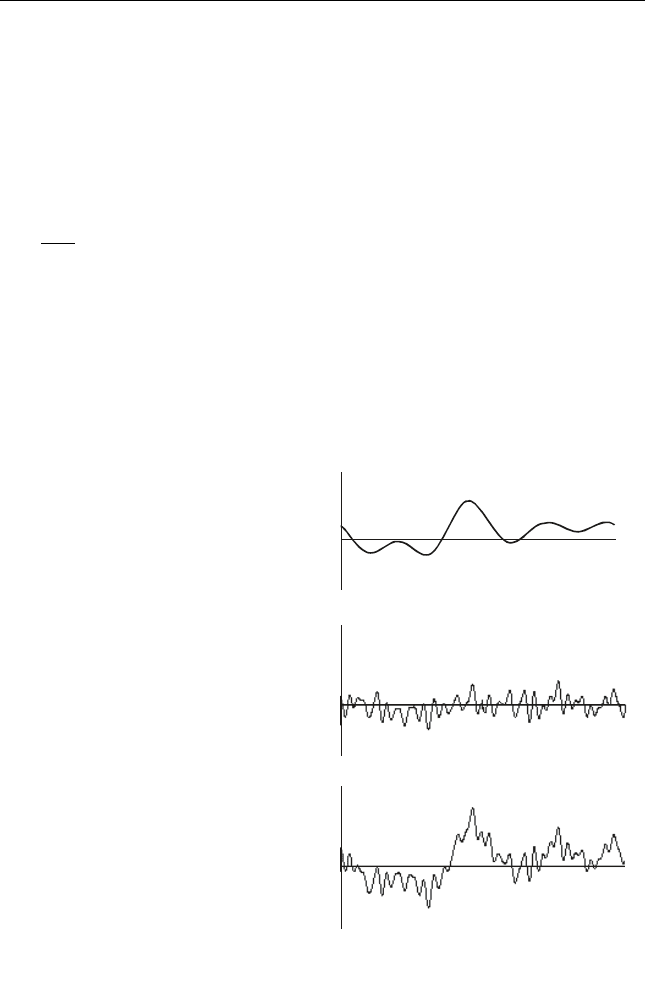
или инвертором. На рис. 2.6 сплошной линией показан исходный

сигнал, пунктиром тот же сигнал, усиленный вдвое, а штриховой

линией – инвертированный сигнал.

Обычно предполагается, что множество сигналов замкнуто от-

носительно умножения на число, таким образом, усиление или ос-

лабление сигнала не нарушает его принадлежности к данному

множеству.

xt ( )

Рис. 2.6. Исходный, усиленный и инвертированный

сигналы

Возможность выполнения указанных операций над сигналами

обусловливает глубокое сходство множества сигналов с линейным

(векторным) пространством. Это позволяет использовать линейное

пространство в качестве модели для множества сигналов, которое в

таком случае становится пространством сигналов.

2.3. ЛИНЕЙНОЕ ПРОСТРАНСТВО

Линейным пространством называется множество

объектов

(векторов), удовлетворяющее следующим аксиомам.

А. Для любых двух векторов из

определена операция сло-

жения, причем сумма вновь принадлежит

(множество

замкнуто относительно сложения), т.е.

:( )x M y M x y M     

(



читается «для всех»).

2.3. Линейное пространство

Выполняются следующие аксиомы сложения:

1) ассоциативность

, , :x y z M

( ) ( )x y z x y z    

;

2) существование нейтрального элемента (нулевого вектора)

0 : : 0M x M x x     



(



читается «существует»);

3) существование противоположного элемента

( ) : ( ) 0x M x M x x       



;

4) коммутативность

,:x y M x y y x    

Перечисленные аксиомы известны в высшей (абстрактной) ал-

гебре, как аксиомы коммутативной группы

по сложению.

Б. Для любого вектора из

определена операция умножения

на скаляр



(элемент некоторого поля



– как правило, поля



вещественных или поля



комплексных чисел)

, причем ре-

зультирующий вектор снова принадлежит

Иными словами,

множество

замкнуто относительно умножения на скаляр:

: .x M x M    

Выполняются следующие аксиомы умножения на скаляр:

1) ассоциативность

( ) ( ) ,x x x x M     

;

2) существование в поле скаляров особого элемента – единицы

1 : :1x M x x    

;

3) дистрибутивность сложения векторов и умножения вектора

на скаляр

( ) , ,

( ) , .

x y x y x y M

x x x x M

      





      







Нетрудно убедиться непосредственной проверкой, что все эти

аксиомы выполняются для сигналов как аналоговых, так и дис-

кретных – вещественных и комплексных. Поэтому сигналы можно

рассматривать как векторы и называть векторами.

В радиотехнике и связи часто используются комплексные сиг-

налы, принимающие значения из поля



комплексных чисел. Да-

лее, если явно не сказано обратное, всегда подразумевается, что

Коммутативная группа называется также абелевой группой в честь Н.Х. Абеля

(1802 – 1829), выдающегося норвежского математика.

Полем в алгебре называется множество с определенными на нем двумя бинар-

ными операциями, называемыми сложением и умножением, которое является

коммутативной группой относительно обеих операций, за исключением суще-

ствования элемента, противоположного по умножению нейтральному по сло-

жению элементу (запрещено деление на нуль). Кроме полей вещественных и

комплексных чисел в теории связи используются конечные поля Галуа (см.

разд. 8).

2. ОСНОВЫ ТЕОРИИ СИГНАЛОВ

сигналы комплексные; вещественные сигналы можно рассматри-

вать как комплексные с нулевой мнимой частью. Таким образом,

далее сигналы считаются элементами комплексного пространства

(компоненты векторов являются комплексными числами и склады-

ваются при сложении векторов, а также умножаются на скаляры по

правилам комплексной арифметики).

Очевидно, множество всех аналоговых сигналов, заданных на

бесконечной временной оси, можно рассматривать как линейное

(векторное) пространство (обозначим его

). Большой практиче-

ский интерес представляет его подмножество – пространство сиг-

налов ограниченной энергии, заданных на бесконечной временной

оси, которое принято обозначать

( , )L  

или просто

. В ча-

стных случаях пространство сигналов сужают, например, до под-

пространства

()LT

сигналов ограниченной энергии, определен-

ных на данном конечном временнóм интервале (сигналов конечной

длительности

тождественно равных нулю вне интервала

[0, ]T

или подпространства

()LF

сигналов с ограниченной полосой час-

тот

. Линейным пространством является и множество

всех

дискретных сигналов ограниченной энергии, заданных на всей

дискретной временной оси

,n   

. Между двумя последними

пространствами, как будет показано ниже, можно установить вза-

имно однозначное соответствие, что делает возможной цифровую

обработку сигналов, изначально аналоговых, с последующим пре-

образованием результата снова в форму аналогового колебания

(см. разд. 12).

Поскольку определено сложение векторов и умножение векто-

ра на скаляр, определена и линейная комбинация конечной сово-

купности произвольных векторов

 

, 1,

x k N





, (2.7)

где

 

, 1,



– произвольный набор скаляров.

Совокупность векторов

 

, 1,



линейно независима, если

равенство

k







возможно лишь при условии



1,kN

. Другими словами, линейная независимость означает, что