Васюков В.Н. Теория электрической связи
Подождите немного. Документ загружается.


2.10. Ряд Фурье и интеграл Фурье
73
ций является переход к непрерывному представлению сигналов из
2
( , )L
интегралом Фурье
2
( ) ( )
j ft
x t X f e df
, (2.45)
где
2
( ) ( )
j ft
X f x t e dt
(2.46)
– спектральная плотность.
Между рядом и интегралом Фурье имеется тесная связь. Рас-
смотрим непериодический сигнал
()xt
конечной длительности
c
.
(Функция, равная нулю всюду за пределами интервала конечной
длины, называемого носителем функции, называется финитной.)
Спектральная плотность
()Xf
сигнала
()xt
определяется выра-
жением прямого преобразования Фурье (2.46). Повторение финит-
ного сигнала
()xt
с периодом
T
, большим, чем длительность
c
,
дает периодический сигнал
( ) ( )
k
x t x t kT
, который в силу
своей периодичности может быть представлен рядом Фурье со
спектральными коэффициентами, определяемыми выражением
(2.41). Сравнивая выражения (2.46) и (2.41) и учитывая, что инте-
грал в бесконечных пределах от финитной функции равен интегра-
лу по интервалу, содержащему носитель функции, можно записать
равенство
2
2
2
11
()
T
j kt
T
k
T
k
C x t e dt X
T T T
. (2.47)
Таким образом, спектральная плотность импульсного сигнала
имеет форму огибающей спектральных коэффициентов ряда Фурье
периодической последовательности, образованной повторением
данного импульсного сигнала с произвольным периодом. Заметим,
что с ростом периода повторения спектральные составляющие
следуют друг за другом по оси частот все более плотно. Неперио-
дический сигнал представляет собой предельный случай периоди-
ческого при
T
, поэтому можно считать (нестрого!), что спек-
тральная плотность – это «сплошная» совокупность спектральных
коэффициентов. Следует, однако, иметь в виду, что «амплитуда»
каждой спектральной составляющей при этом также стремится к
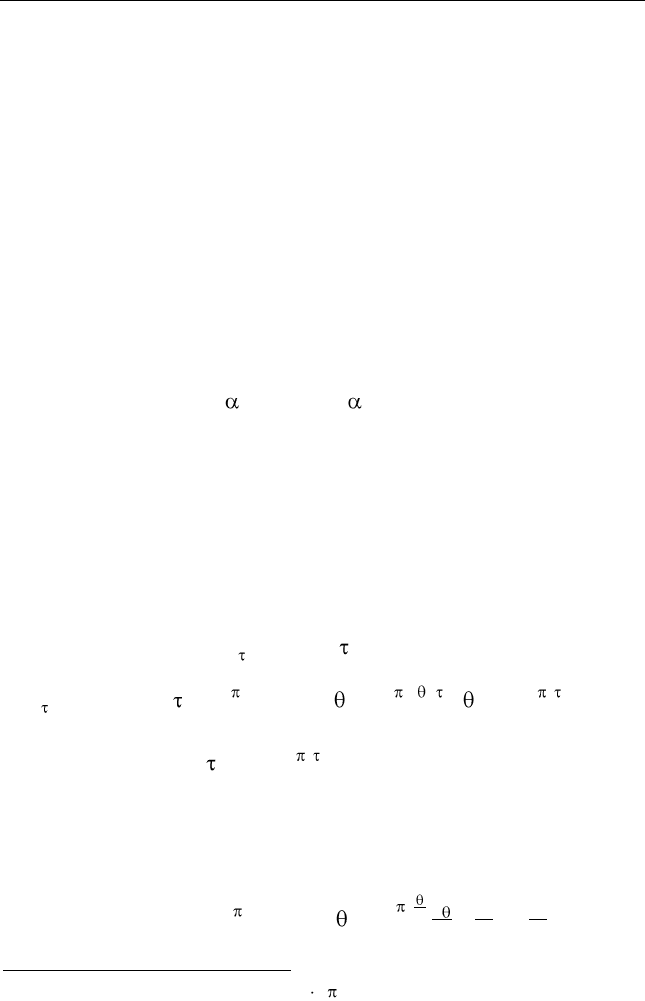
2. ОСНОВЫ ТЕОРИИ СИГНАЛОВ
74
нулю, в отличие от спектральной плотности. Кроме того, не следу-
ет забывать, что для сигнала
()xt
, имеющего размерность напря-
жения, спектральная плотность
()Xf
имеет размерность
[Вольт/Герц], в то время как единицей измерения коэффициентов
ряда Фурье (2.41) является Вольт
35
. Поэтому спектр периодическо-
го сигнала и спектральная плотность финитного сигнала – два раз-
личных объекта. Тем не менее формальное сходство, выражаемое
формулой (2.47), можно использовать, например, для расчета спек-
тра последовательности, полученной периодическим повторением
финитного сигнала с известной спектральной плотностью.
Рассмотрим основные свойства преобразования Фурье, кото-
рые полезно знать при практическом его использовании. Для крат-
кости будем использовать обозначение
( ) ( )x t X f
для функций
времени и частоты, связанных парой преобразований Фурье.
1. Линейность
( ) ( )
k k k k
kk
x t X f
.
2. Дуальность (частотно-временная симметрия)
( ) ( )x f X t
, (2.48)
где
()x
понимается как спектральная плотность временной функ-
ции
()X
.
Читателю предлагается доказать это свойство в качестве уп-
ражнения.
3. Теорема сдвига
Рассмотрим сигнал
( ) ( )x t x t
. Его спектральная плотность
2 2 ( ) 2
( ) ( ) ( ) ( )
j ft j f j f
X f x t e dt x e d e X f
.
Таким образом,
2
( ) ( )
jf
x t e X f
.
4. Теорема изменения масштаба
Рассмотрим сигнал
( ) ( )
m
x t x mt
, представляющий собой сиг-
нал
()xt
, сжатый по оси времени в
m
раз,
0m
. Его спектральная
плотность
2
2
1
( ) ( ) ( )
m
jf
j ft
d
m
m
f
X f x mt e dt x e X
mm
. (2.49)
35
Подразумевается, что функция
exp( 2 )j ft
физической размерности не имеет.

2.10. Ряд Фурье и интеграл Фурье
75
Теперь положим, что множитель
0m
. Тогда
2
2
( ) ( ) ( )
jf
j ft
d
m
X f x t e dt x e
2
11
()
f
j
f
x e d X
. (2.50)
Итак, объединяя (2.49) и (2.50), можно окончательно записать
1
()
f
x mt X
mm
.
5. Теорема дифференцирования
Обозначим через
( ) ( )
d
x t dx t dt
производную по времени
сигнала
()xt
. Спектральная плотность производной равна
2 2 2
()
( ) ( ) 2 ( )
j ft j ft j ft
d
dx t
X f e dt x t e j f x t e dt
dt
.
Здесь использована формула интегрирования по частям. Первое
слагаемое полученного выражения равно нулю, так как сигнал
()xt
в силу принадлежности
2
( , )L
, т.е. ограниченности энергии,
стремится к нулю при
t
. Таким образом,
()
2 ( )
dx t
j f X f
dt
.
6. Теорема интегрирования
Обратной к теореме дифференцирования является теорема ин-
тегрирования
1 (0) ( )
( ) ( )
22
t
Xf
x t dt X f
jf
. (2.51)
7. Теорема модуляции
Под модуляцией здесь подразумевается умножение сигнала
()xt
на комплексную экспоненциальную функцию
0
2j f t
e
:
00
2 2 ( )
2
0
( ) ( ) ( )
j f t j f f t
j ft
x t e e dt x t e dt X f f
,
так что
0
2
0
( ) ( )
j f t
x t e X f f
.

2. ОСНОВЫ ТЕОРИИ СИГНАЛОВ
76
8. Теорема свѐртки
( ) ( ) ( ) ( )x t y t X f Y f
была фактически доказана в разд. 2.9.
9. Теорема умножения
( ) ( ) ( ) ( )x t y t X f Y f
справедлива в силу теоремы свѐртки и свойства дуальности преоб-
разования Фурье.
10. Теорема сопряжения
Если комплексному сигналу
()xt
соответствует спектральная
плотность
()Xf
, то для комплексно сопряженного сигнала спра-
ведливо соответствие
**
( ) ( )x t X f
:
*
* 2 2 ( ) *
( ) ( ) ( )
j ft j f t
x t e dt x t e dt X f
.
11. Теорема обращения
Обращение сигнала означает перемену знака аргумента (време-
ни). Обозначим сигнал
()xt
, обращенный во времени,
_( ) ( )x t x t
. Его спектральная плотность:
22
( ) ( ) ( ) ( )
j ft j f
X f x t e dt x e d
2 ( )
( ) ( )
jf
x e d X f
,
так что обращение временнóй оси в обычном временнóм описании
сигнала эквивалентно обращению оси частотной в его спектраль-
ном представлении:
( ) ( )x t X f
.
Рассмотренные свойства преобразования Фурье справедливы
для произвольных комплексных сигналов. На практике часто име-
ются дополнительные сведения о сигнале, которые позволяют уп-
ростить решение задачи спектрального анализа с учѐтом частных
свойств спектральных плотностей.
Например, предположение о том, что сигнал
()xt
является ве-
щественным, приводит к свойству сопряженной симметрии спек-
тральной плотности:
*
( ) ( )X f X f
,

2.10. Ряд Фурье и интеграл Фурье
77
или, что равносильно,
( ) ( )X f X f
и
arg ( ) arg ( )X f X f
.
В самом деле,
**
2 2 2 ( )
( ) ( ) ( ) ( )
j ft j ft j f t
X f x t e dt x t e dt x t e dt
.
Это обстоятельство следует учитывать при решении практиче-
ских задач, так как в большинстве случаев рассматриваются имен-
но вещественные сигналы. В частности, такая симметрия спектра
(спектральной плотности) используется в технике связи: для
уменьшения требуемой пропускной способности каналов связи
применяются амплитудно-модулированные сигналы с одной боко-
вой полосой (ОБП-сигналы).
Если сигнал является вещественным и четным, то его спек-
тральная плотность также вещественна и чѐтна:
( ) ( )X f X f
.
Это утверждение следует из того, что обращение во времени не
изменяет вещественного чѐтного сигнала, а следовательно, не
влияет и на его спектральную плотность, которая должна, таким
образом, быть инвариантной к обращению частоты, т.е. вещест-
венной и чѐтной.
Если сигнал является вещественным и нечетным, то его спек-
тральная плотность – мнимая и нечетная:
( ) ( )X f X f
.
Действительно, обращение во времени изменяет знак нечѐтного
сигнала, следовательно, его спектральная плотность также должна
при обращении частоты лишь менять знак, но, поскольку спек-
тральная плотность вещественного сигнала сопряженно-
симметрична, отсюда следует, что еѐ вещественная часть равна
нулю, т.е. спектральная плотность является мнимой.
Спектральная плотность сигнала
0
2j f t
e
как «обычная функ-
ция» не существует, так как
0
2j f t
e
не принадлежит пространству
2
( , )L
. В то же время решение многих задач упрощается, если
все же определить спектральную плотность комплексной экспо-
ненты в терминах теории обобщенных функций. Отыскание спек-
тральной плотности сигнала
0
2j f t
e
сводится к нахождению пря-
мого преобразования Фурье отрезка функции
0
2j f t
e
длительности

2. ОСНОВЫ ТЕОРИИ СИГНАЛОВ
78
и предельному переходу при
. В том, что спектральная
плотность сигнала
0
2j f t
e
представляет собой -функцию (являет-
ся сингулярной)
36
, легко убедиться, если найти сигнал, соответст-
вующий спектральной плотности
0
()ff
, через обратное преоб-
разование Фурье:
0
2
2
0
()
j f t
j ft
f f e df e
.
Спектральные плотности гармонических сигналов
0
cos(2 )ft
и
0
sin(2 )ft
легко находятся с учетом формул Эйлера:
0 0 0
1
cos(2 ) ( ) ( )
2
f t f f f f
,
0 0 0
1
sin(2 ) ( ) ( )
2
f t f f f f
j
.
Пример 2.20. Балансно-модулированное колебание (см. разд. 5)
может быть получено путем перемножения модулирующего сигна-
ла
()xt
и несущего гармонического колебания
0
cos(2 )ft
. Спек-
тральную плотность балансно-модулированного сигнала можно
найти, воспользовавшись теоремой умножения с учетом вида спек-
тральной плотности косинусоидального колебания:
00
0
( ) ( )
( )cos(2 )
22
X f f X f f
x t f t
.
Тот же результат можно получить на основе теоремы модуляции и
свойства линейности преобразования Фурье. ◄
Во многих задачах одновременно присутствуют периодические
и непериодические сигналы. Для того чтобы можно было пользо-
ваться общим математическим аппаратом интеграла Фурье, найдем
спектральную плотность
T
-периодического сигнала, который
можно записать в виде ряда Фурье
2
()
j kt
T
k
k
x t C e
.
36
От англ. single – единственный; в названии отражается тот факт, что вся спек-
тральная «масса» сосредоточена в одной точке частотной оси.

2.10. Ряд Фурье и интеграл Фурье
79
Учитывая линейность преобразования Фурье и зная спектраль-
ную плотность комплексной экспоненциальной функции, запишем
спектральную плотность в виде
2
()
k
k
X f C f k
T
. (2.52)
Таким образом, спектральная плотность периодического сигна-
ла сингулярна, т.е. состоит из -функций, сосредоточенных на
частотах, кратных частоте повторения сигнала.
2.10.3. КОРРЕЛЯЦИОННО-СПЕКТРАЛЬНЫЕ
ХАРАКТЕРИСТИКИ ДЕТЕРМИНИРОВАННЫХ
СИГНАЛОВ
Согласно обобщенной формуле Рэлея (2.20) скалярное про-
изведение двух детерминированных сигналов может быть найдено
как во временной, так и в частотной области:
**
( , ) ( ) ( ) ( ) ( )x y x t y t dt X f Y f df
.
Подынтегральное выражение правой части этого равенства
*
( ) ( ) ( )
xy
W f X f Y f
называется взаимной спектральной плотностью сигналов
()xt
и
()yt
.
В частном случае при
( ) ( )x t y t
взаимная спектральная плот-
ность превращается в энергетический спектр сигнала
2
( ) ( )
x
W f X f
.
Смысл энергетического спектра выясняется, если выразить
энергию сигнала через скалярное произведение
*
( , ) ( ) ( ) ( )
xx
E x x X f X f df W f df
.
Таким образом, функция
()
x
Wf
описывает распределение
энергии сигнала по частотной оси (поэтому правильнее было бы
называть ее спектральной плотностью энергии). Заметим, что

2. ОСНОВЫ ТЕОРИИ СИГНАЛОВ
80
спектральная плотность сигнала
()Xf
является комплексной
функцией, аргумент которой теряется при переходе от
()Xf
к
()
x
Wf
, поэтому в общем случае сигнал нельзя восстановить по
его энергетическому спектру
37
.
Взаимная спектральная плотность характеризует сходство сиг-
налов в том смысле, что интеграл от нее равен их скалярному про-
изведению. В частности, для ортогональных сигналов взаимная
спектральная плотность такова, что при интегрировании дает 0, т.е.
различные частотные составляющие взаимной спектральной плот-
ности ортогональных сигналов при интегрировании компенсируют
друг друга.
Для энергетического спектра и взаимной спектральной плотно-
сти, как функций частоты, можно определить при помощи обрат-
ного преобразования Фурье (если оно существует) соответствую-
щие временные функции. Запишем вначале обратное
преобразование Фурье для взаимной спектральной плотности
2 * 2
( ) ( ) ( ) ( )
j f j f
xy xy
B W f e df X f Y f e df
.
Обозначим
* 2 *
( ) ( )
jf
Y f e Y f
, где
2
( ) ( )
jf
Y f Y f e
–
спектральная плотность сигнала
( ) ( )y t y t
, равного сигналу
()yt
, задержанному на величину . Тогда
**
( ) ( ) ( ) ( ) ( ) ( , )
xy
B X f Y f df x t y t dt x y
.
Полученная функция характеризует сходство сигнала
()xt
и
сигнала
( ) ( )y t y t
в зависимости от значения сдвига, и назы-
вается взаимно корреляционной функцией (ВКФ) детерминирован-
ных сигналов
()xt
и
()yt
.
Аналогично функция
2 * 2
( ) ( ) ( ) ( )
j f j f
xx
B W f e df X f X f e df
,
37
Заметим, что в частных случаях это можно сделать, если имеются дополнитель-
ные сведения, например о том, что
()Xf
есть вещественная четная функция.

2.10. Ряд Фурье и интеграл Фурье
81
характеризующая сходство сигнала
()xt
и его задержанной копии
( ) ( )x t x t
**
( ) ( ) ( ) ( ) ( ) ( , )
x
B X f X f df x t x t dt x x
, (2.53)
называется автокорреляционной функцией (АКФ) детерминиро-
ванного сигнала.
Автокорреляционная функция обладает некоторыми свойства-
ми, которые важно знать для ее правильного использования.
1. Автокорреляционная функция достигает максимума при
0
и равна при этом значении аргумента энергии сигнала:
(0) max ( )
x x x
B B E
. (2.54)
Доказать это свойство легко при помощи неравенства Шварца.
2. Автокорреляционная функция обладает свойством сопря-
женной симметрии:
**
( ) ( ) ( ) ( ) ( )
x
B x t x t dt x x d
*
**
( ) ( ) ( )
x
x x d B
.
В частности, АКФ вещественного сигнала – четная функция.
Взаимно корреляционная функция указанными свойствами не
обладает: например, для ортогональных сигналов она равна нулю
при нулевом сдвиге; в остальном ее форма определяется формами
обоих сигналов.
Введенные функции играют очень важную роль, в частности,
при выборе сигналов для синхронизации систем связи, что иллюст-
рируется следующим примером.
Пример 2.21. Многие системы связи нуждаются в синхрониза-
ции, т.е. в одновременном начале (с точки зрения устройств пере-
дачи и приема) интервалов времени, в течение которых передаются
и принимаются сигналы
38
. Для того чтобы синхронизировать при-
емник, необходимо время от времени передавать некоторый спе-
38
Говоря здесь об одновременности, мы для простоты не учитываем время пере-
дачи сигнала по каналу связи.
2. ОСНОВЫ ТЕОРИИ СИГНАЛОВ
82
циальный сигнал, играющий роль временнóй метки, временнóе
положение которой приемник должен измерить, чтобы «сверить
часы». Измерение временнóго положения синхронизирующего
сигнала производится при помощи многоканального устройства,
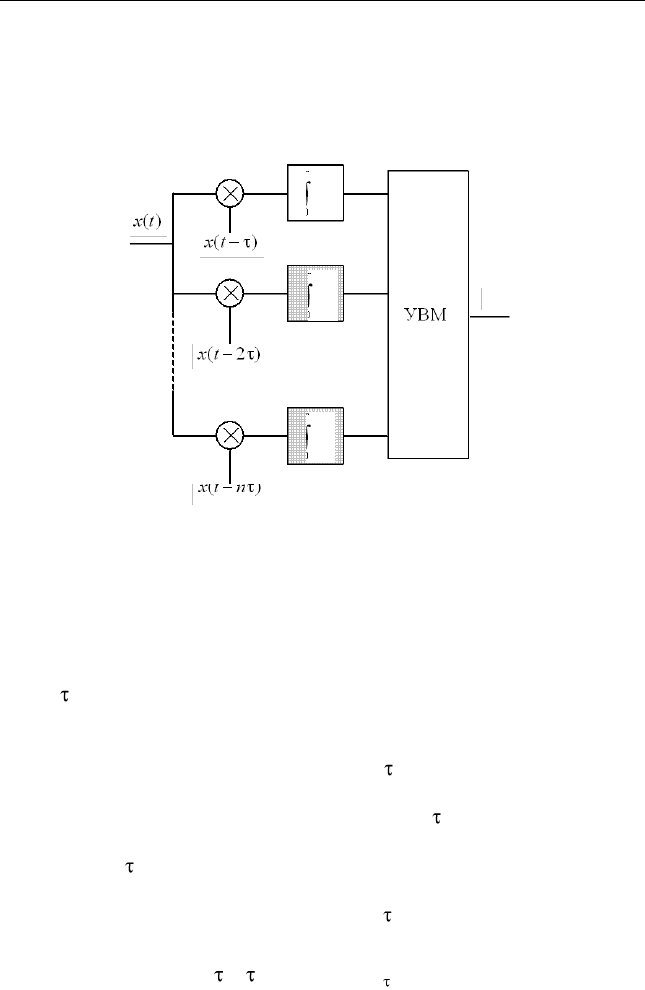
структурная схема которого показана на рис. 2.26.
Рис. 2.26. Измерение временнόго положения
синхронизирующего сигнала
В каждом канале вырабатывается значение взаимно корреляци-
онной функции принятого сигнала и одного из
n
опорных сигна-
лов; каждый из опорных сигналов представляет собой копию
входного сигнала, задержанную на величину, кратную некоторому
шагу . Шаг выбирается исходя из требуемой точности измерения
задержки, при этом для достижения большей точности шаг необ-
ходимо уменьшать. Число каналов
n
определяется диапазоном из-
меряемых задержек и величиной шага . Легко видеть, что вели-
чины на выходах интеграторов представляют собой отсчеты АКФ
принимаемого сигнала, взятые с интервалом .
С учетом 1-го свойства АКФ, если задержка входного сигнала
составляет
k
, то на выходе
k
-го канала значение ВКФ достигнет
максимума и будет равно энергии сигнала. Устройство выбора
максимума УВМ вырабатывает оценку
по номеру канала, на вы-
ходе которого имеет место максимальное значение интеграла
arg max( , )
k
k
xx
◄
