Васюков В.Н. Теория электрической связи

Подождите немного. Документ загружается.

3.1. Случайные величины и их характеристики

113

чального момента) возможно только в том случае, если вся «веро-

ятностная масса» сосредоточена в точке

0x 

. Таким образом,

роль нулевого вектора в рассматриваемом пространстве играет

случайная величина, которая принимает значение 0 с вероятностью

1 (ПРВ такой случайной величины равна

()x

Норма случайной величины определяется через скалярное про-

изведение, как

( , )x x x x

, а метрика задается через норму

( , ) ( )d x y x y x y   

Итак, множество случайных величин, определенных на общем

пространстве элементарных событий, становится гильбертовым

пространством. К нему применимы все ранее введенные для гиль-

бертова пространства понятия, такие, как базис, ортонормальный

базис, ортогонализация Грама – Шмидта, равенство Парсеваля и т.п.

В следующем примере предполагается, что математическое

ожидание случайных величин равно нулю, тогда средний квадрат

совпадает с дисперсией, а корреляционный момент – с ковариаци-

онным (вторым смешанным центральным моментом).

Пример 3.3. Задача оптимальной фильтрации состоит в том,

чтобы по наблюдаемому колебанию

()zt

наилучшим образом оце-

нить полезный (случайный) сигнал

()xt

. И наблюдаемый, и полез-

ный сигналы здесь будем понимать, как наборы случайных вели-

чин – отсчетов сигнала (их множество может быть несчетным, т.е.

«сплошным»). Оптимальный линейный фильтр – это линейный

оператор

{}

, вырабатывающий на основе колебания

()zt

оценку,

такую, что дисперсия ошибки оценивания

[ ( ) { ( )}]x t z t 

мини-

мальна.

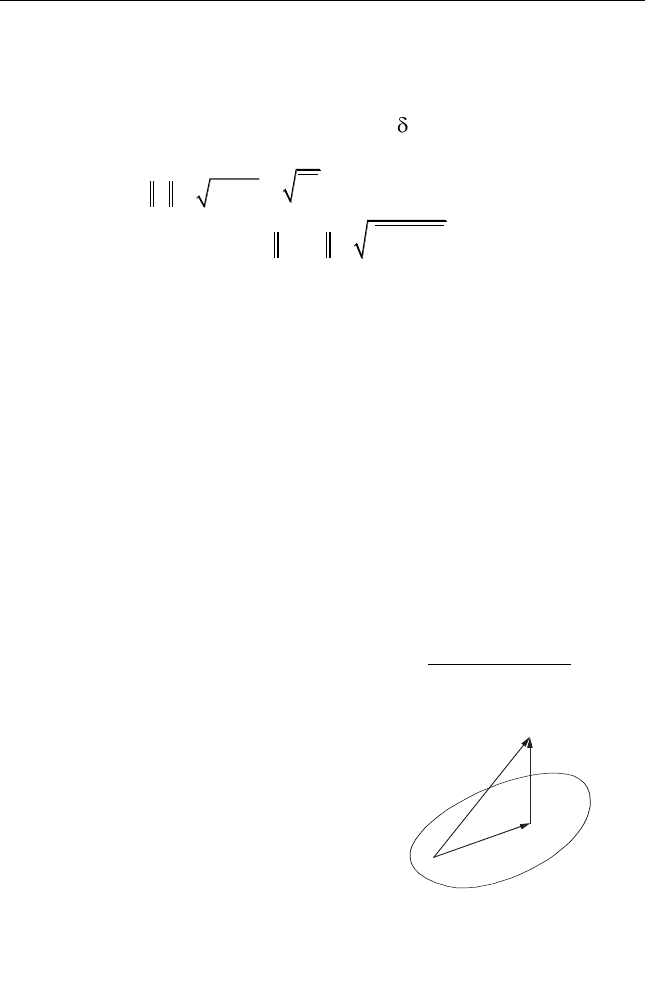
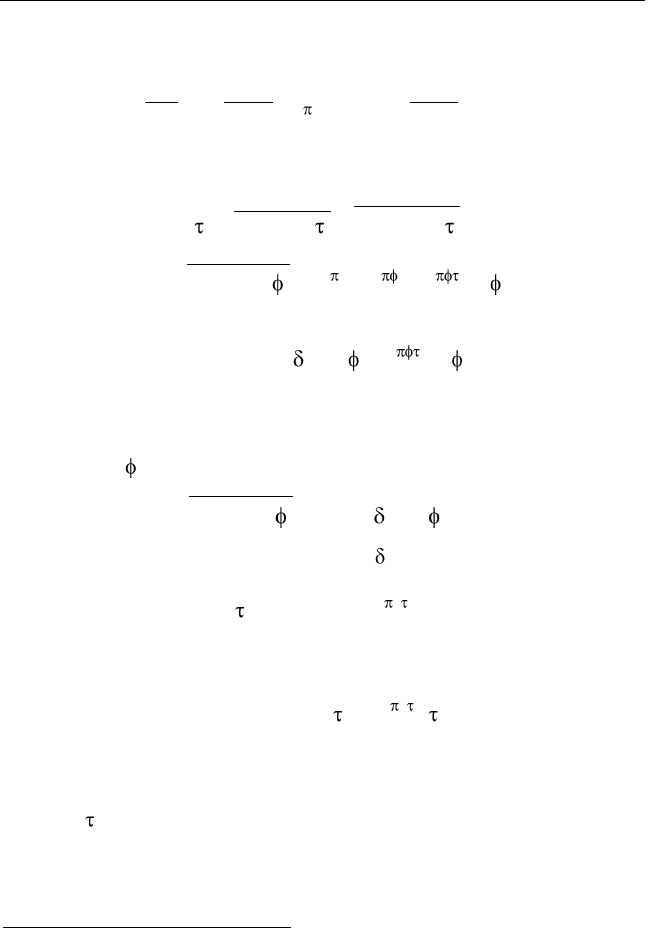
Результат воздействия на сигнал

()zt

линейного оператора – это, нестро-

го говоря, линейная комбинация всех

отсчетов сигнала. Поэтому оценка

принадлежит линейной оболочке отсче-

тов сигнала

()zt

, или подпространст-

ву, натянутому на эти отсчеты (кото-

рые представляют собой случайные

величины, т.е. векторы). Полезный сиг-

нал

()xt

в общем случае лежит вне это-

го подпространства (рис. 3.4) .

xt()

[ ()– { ()}]xt zt

{()}zt

Рис. 3.4. Геометрическая

интерпретация принципа

оптимального линейного

оценивания

3. СЛУЧАЙНЫЕ ПРОЦЕССЫ

114

Из геометрических соображений ясно, что СКО ошибки оцени-

вания (норма ошибки) будет минимально в том случае, если вектор

ошибки будет ортогонален этому подпространству (ошибка не

коррелирована с наблюдаемым сигналом в произвольный момент

времени ), отсюда условие оптимальности оператора

[ ( ) { ( )}] ( ) 0x t z t z

Учитывая, что линейный оператор выражается интегралом, для

оптимальной линейной оценки получаем

( ) ( , ) ( ) ( ) 0x t h t z d z















где

( , )ht

– весовая функция (ядро оператора), имеющая смысл

отклика фильтра в момент времени

на значение наблюдаемого

сигнала в момент ; – переменная, имеющая размерность вре-

мени. Раскрывая скобки и выполняя усреднение, получаем

( ) ( ) ( , ) ( ) ( ) 0x t z h t z z d









откуда следует уравнение Винера – Хопфа

( , ) ( , ) ( , )

zz xz

h t k d k t









где

( , ) ( ) ( )

k z z

– второй смешанный момент отсчетов слу-

чайного процесса

()zt

в моменты времени и , называемый

функцией автокорреляции процесса

()zt

, а

( , ) ( ) ( )

k t x t z

–

второй смешанный момент отсчетов различных процессов, назы-

ваемый функцией взаимной корреляции процессов

()xt

()zt

(см. п. 3.2).

Характеристика

( , )ht

оптимального линейного устройства

оценивания находится, как решение уравнения Винера – Хопфа

(подробнее см. разд. 10).◄

3.2. СЛУЧАЙНЫЕ ПРОЦЕССЫ И ИХ ОПИСАНИЕ

В теории связи большую роль играют случайные процессы, яв-

ляющиеся математическими моделями как сигналов, так и помех.

Случайный процесс – это колебание, принимающее в любой за-

данный момент времени значение, которое невозможно точно

3.2. Случайные процессы и их описание

115

предсказать. Таким образом, можно понимать случайный процесс

как упорядоченную последовательность случайных величин, сле-

дующих друг за другом в порядке возрастания некоторой перемен-

ной (чаще всего времени). Перейти от описания случайной вели-

чины к описанию случайного процесса можно, рассматривая

совместные распределения двух значений процесса в различные

моменты времени, трех значений и т.д. В частности, рассматривая

процесс в

временных сечениях (при

,...,

t t t

), получаем

-мер-

ные совместные функцию распределения и плотность распределе-

ния вероятностей случайных величин

( ),xt

…

()

, определяемые

выражением

 

1 1 1 1 1

,..., ( ,..., ) ... ( ,..., ) ...

n n n n n

x x F x x w x x dx dxP

 

   



Здесь и далее зависимость от времени явно не указана для упроще-

ния записи. Для

-мерной ПРВ выполняется условие нормировки

... ( ,..., ) ... 1

w x x dx dx



 





Случайный процесс считается полностью определенным, если

для любого

можно записать его совместную ПРВ при любом

выборе моментов времени

,...,

. Следует отметить, что на прак-

тике это удается сделать крайне редко

Часто при описании случайного процесса можно ограничиться

совокупностью его смешанных начальных моментов (если они су-

ществуют, т.е. сходятся соответствующие интегралы)

... 1 1 1

... ... ( ,..., ) ...

k k n n n

m x x w x x dx dx



 





(3.6)

и смешанных центральных моментов

... 1 1 1

... ( ) ...( ) ( ,..., ) ...

k k x n x n n

M x m x m w x x dx dx



 

  



(3.7)

при целых неотрицательных

,...,

и целом

Исключение составляют гауссовские и марковские процессы, а также

процессы с распределением Гиббса.

3. СЛУЧАЙНЫЕ ПРОЦЕССЫ

116

В частности, полагая в (3.6)

1k 

... 0

kk  

, получаем

первый начальный момент (математическое ожидание) при

tt

;

при

2k 

... 0

kk  

выражение (3.6) определяет средний

квадрат, а выражение (3.7) – дисперсию в соответствующем сече-

нии. Если под случайным процессом подразумевается сигнал в

форме напряжения, то математическое ожидание имеет смысл его

среднего значения («медленной» составляющей), средний квад-

рат – полной мощности, а дисперсия – мощности флюктуационной

(«быстрой») составляющей.

В общем случае моменты совместной ПРВ зависят от располо-

жения сечений на оси времени и называются моментными функ-

циями. Чаще всего используют второй смешанный центральный

момент

11 1 2 1 2 1 2 1 2

( , ) ( )( ) ( , ) .

x x x

M R t t x m x m w x x dx dx



 

    



( )( )

x m x m  

называемый функцией автокорреляции или автокорреляционной

функцией

(АКФ). Напомним, что здесь и далее явно не указана

зависимость от времени, в частности, функциями времени являют-

ся

()

m m t

()

m m t

Можно рассматривать совместно два случайных процесса

()xt

()yt

, которые в общем случае не являются независимыми в веро-

ятностном смысле; такое рассмотрение предполагает их совмест-

ное описание в виде совместной многомерной ПРВ, а также в виде

совокупности всех моментов, в том числе смешанных. Наиболее

часто при этом используют второй смешанный центральный мо-

мент

1 2 1 2 1 2 1 2

( , ) ( )( ) ( , )

xy x y

R t t x m y m w x y dx dy



 

   



( )( )

x m y m  

Ни в коем случае не следует путать понятия АКФ для случайных про-

цессов и для детерминированных сигналов, которые имеют совершенно

разный смысл!

3.2. Случайные процессы и их описание

117

называемый взаимно корреляционной функцией

( , )

R t t

. Как и

АКФ, взаимно корреляционная функция (ВКФ) является функцией

двух переменных.

Среди всех случайных процессов выделяют СП, для которых

совместная

-мерная ПРВ не изменяется при одновременном из-

менении (сдвиге) всех моментов времени на одну и ту же величи-

ну. Такие процессы называются стационарными в узком смысле,

или строго стационарными.

Чаще всего на практике ограничивают рассмотрение случай-

ными процессами с ослабленным условием стационарности. СП

называется стационарным в широком смысле, если при одновре-

менном сдвиге сечений не изменяются лишь его моменты не выше

второго порядка. Практически это означает, что СП

()xt

стациона-

рен в широком смысле, если он имеет постоянные среднее (мате-

матическое ожидание

) и дисперсию

, а АКФ зависит только

от разности моментов времени, но не от их положения на

временнóй оси:

()

m t m

1 2 2 1

( , ) ( ) ( )

x x x

R t t R t t R  

Заметим, что

(0)

RD

, откуда и следует постоянство диспер-

сии.

Нетрудно убедиться, что процесс, стационарный в узком смыс-

ле, стационарен и в широком смысле. Обратное вообще неверно,

хотя существуют процессы, для которых стационарность в широ-

ком смысле означает и стационарность в узком смысле.

Пример 3.4. Совместная

-мерная ПРВ отсчетов

,...,

гаус-

совского процесса, взятых в моменты времени

,...,

, имеет вид

()

2| |

/ 2 1/ 2

( , ,...., )

(2 ) .... | |

w x x x e









(3.8)

где

– определитель квадратной матрицы, составленной из по-

парных коэффициентов корреляции отсчетов;

– алгебраиче-

ское дополнение элемента

этой матрицы.

Как видно из выражения (3.8), совместная ПРВ полностью оп-

ределяется математическими ожиданиями, дисперсиями и коэффи-

3. СЛУЧАЙНЫЕ ПРОЦЕССЫ

118

циентами корреляции отсчетов. Таким образом, зная моментные

функции не выше второго порядка, при любом

можно записать

совместную ПРВ. Если процесс стационарен в широком смысле,

то все математические ожидания одинаковы, все дисперсии (а зна-

чит, и СКО) равны друг другу, а коэффициенты корреляции опре-

деляются только тем, насколько моменты времени

,...,

отстоят

друг от друга. Тогда, очевидно, ПРВ (3.8) не изменится, если все

моменты

,...,

сдвинуть влево или вправо на одну и ту же вели-

чину. Отсюда следует, что гауссовский процесс, стационарный

в широком смысле, стационарен и в узком смысле (строго ста-

ционарен). ◄

Среди стационарных случайных процессов часто выделяют бо-

лее узкий класс эргодических случайных процессов. Для эргодиче-

ских процессов моменты, найденные усреднением по ансамблю,

равны соответствующим моментам, найденным усреднением по

времени

единственной реализации

()t

   

( ) lim ( )

m x t t dt







   

( ) lim ( )

M x t m t m dt



   



(здесь



– символическое обозначение оператора усреднения по

времени).

В частности, для эргодического процесса математическое ожи-

дание, дисперсия и АКФ равны соответственно:

( ) lim ( )

m x t t dt







   

( ) lim ( )

D x t m t m dt



   



  

( ) ( ) ( ) ( ) ( )R x t m x t m x t x t m       

lim ( ) ( ) .

t t dt m



  



Строгое определение эргодичности выходит за рамки учебника (см.,

напр., [7]).

3.2. Случайные процессы и их описание

119

Эргодичность представляет собой весьма желательное свойст-

во, так как дает возможность практически измерять числовые ха-

рактеристики случайного процесса. Дело в том, что обычно на-

блюдателю доступна лишь одна (хотя, возможно, достаточно

длинная) реализация случайного процесса. Эргодичность означает,

по существу, то, что эта единственная реализация является полно-

правным представителем всего ансамбля.

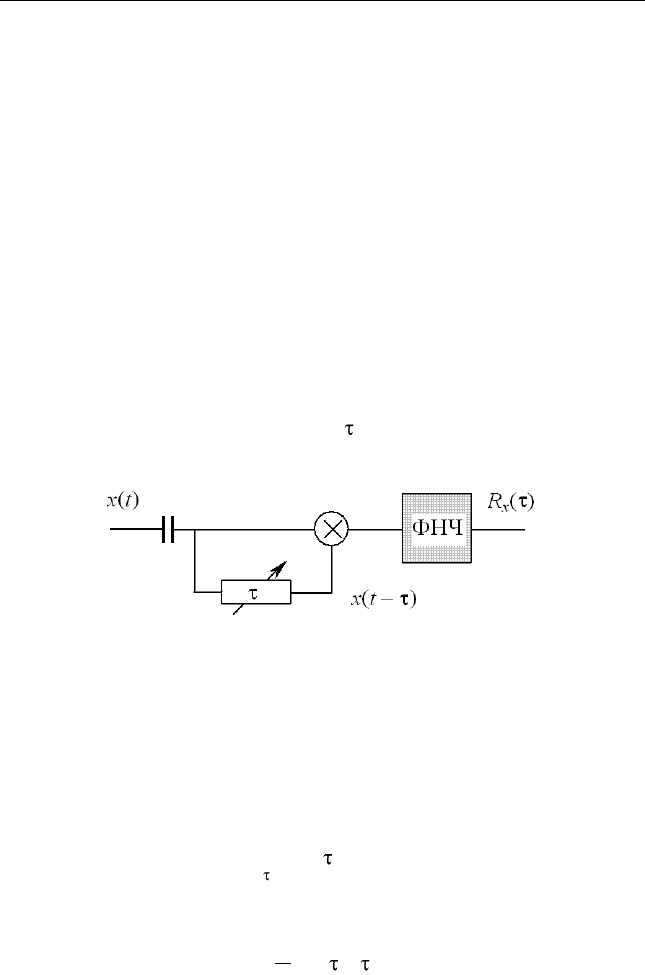
Пример 3.5. Измерение характеристик эргодического процесса

может быть выполнено при помощи простых измерительных уст-

ройств; так, если процесс представляет собой напряжение, завися-

щее от времени, то вольтметр магнитоэлектрической системы

измеряет его математическое ожидание (постоянную составляю-

щую), вольтметр электромагнитной или термоэлектрической сис-

темы, подключенный через разделительную емкость (для исклю-

чения постоянной составляющей), – его среднеквадратическое

значение (СКО). Устройство, структурная схема которого показана

на рис. 3.5, позволяет измерить значения функции автокорреляции

при различных значениях задержки .

Рис. 3.5. Измерение автокорреляционной функции

эргодического процесса

Фильтр нижних частот играет здесь роль интегратора, конден-

сатор выполняет центрирование процесса, так как не пропускает

постоянную составляющую тока. Это устройство называется кор-

релометром.◄

Достаточными условиями эргодичности стационарного слу-

чайного процесса служат условие стремления АКФ к нулю

lim ( ) 0R





а также менее сильное условие Слуцкого

lim ( ) 0







3. СЛУЧАЙНЫЕ ПРОЦЕССЫ

120

3.3. КОРРЕЛЯЦИОННО-СПЕКТРАЛЬНАЯ ТЕОРИЯ

СЛУЧАЙНЫХ ПРОЦЕССОВ

Точное решение задач, связанных с анализом случайных про-

цессов и их воздействия на ЛИС-цепи, сопряжено с большими

трудностями, так как предполагает отыскание совместной

-мерной

ПРВ для выходного процесса. Значительно проще решается задача

анализа, если интересоваться только моментными характеристиками

первого и второго порядка, которые определяют свойство стацио-

нарности в широком смысле. Учитывая, что большинство реально

наблюдаемых процессов удовлетворительно описываются гауссов-

ской моделью, а гауссовские процессы полностью определяются

моментными характеристиками не выше второго порядка, во многих

случаях ограничиваются анализом на уровне математических ожи-

даний (средних) и корреляционных функций.

Рассмотрим вещественный стационарный случайный процесс

()xt

с нулевым средним. Его реализация, как детерминированная

функция, может быть представлена обратным преобразованием

Фурье

( ) ( )

j ft

t f e df











где

()f

– спектральная плотность реализации. (Следует иметь в

виду, что почти все

реализации стационарного СП не принадле-

жат пространству сигналов конечной энергии

, поэтому их

спектральные плотности можно рассматривать лишь в терминах

обобщенных функций, так как соответствующие интегралы в клас-

сическом смысле расходятся. Однако, поскольку нас будут интере-

совать лишь усредненные величины и функции, важна лишь ин-

тегрируемость соответствующих математических ожиданий.)

Случайный процесс

()xt

можно записать в виде

( ) ( )

j ft

x t X f e df











где

()Xf

– также случайный процесс (в соответствии с природой

преобразования Фурье – это тот же процесс, представленный в

другом «базисе»). Выясним, что это за процесс.

Заметим, что здесь выражение «почти все» понимается в строгом веро-

ятностном смысле и означает «с вероятностью единица».

3.3. Корреляционно-спектральная теория cлучайных процессов

121

Поскольку

()xt

– случайный процесс с нулевым средним,

()Xf

также имеет нулевое среднее:

( ) ( ) 0 ( ) 0

j ft

x t X f e df X f







   



Автокорреляционная функция вещественного процесса

()xt

( ) ( ) ( ) ( ) ( )

R x t x t x t x t

    

* 2 2 2

( ) ( )

j ft j t j

X f X e e e dfd



   

 





( ) ( )

W f f e dfd





 





Последнее равенство записано на том основании, что АКФ не

зависит от переменной

, а это может быть только при том усло-

вии, что

f 

, т.е.

( ) ( ) ( ) ( )

X f X W f f



. (3.9)

С учетом стробирующего свойства -функции можно записать

( ) ( )

R W f e df











, (3.10)

а следовательно,

( ) ( )

W f R e d











. (3.11)

Выражения (3.10) – (3.11) составляют запись теоремы Винера –

Хинчина

При

0

из выражения (3.10) следует

(0) ( )

R W f df









Александр Яковлевич Хинчин (1894 – 1959) – русский математик, из-

вестен своими трудами в области теории вероятностей, теории функ-

ций, теории массового обслуживания и др.

3. СЛУЧАЙНЫЕ ПРОЦЕССЫ

122

а поскольку

(0)

RD

– мощность случайного процесса (с нуле-

вым средним), функция

()

называется спектральной плотно-

стью мощности (СПМ). Очевидно, СПМ – неотрицательная функ-

ция. Если процесс имеет ненулевое математическое ожидание

то к СПМ добавляется слагаемое

()mf

Для вещественного процесса АКФ – четная вещественная

функция, тогда СПМ – тоже четная вещественная. Поэтому иногда

используется односторонняя СПМ:

( ) ( )cos(2 )

R N f f df







Очевидно,

( ) 2 ( ), 0.

N f W f f

Иногда нет необходимости знать точный вид АКФ и СПМ и

можно ограничиться числовыми характеристиками, в роли кото-

рых выступают интервал корреляции и эффективная ширина спек-

тра. Интервал корреляции определяют по-разному, в частности,

известны следующие определения.

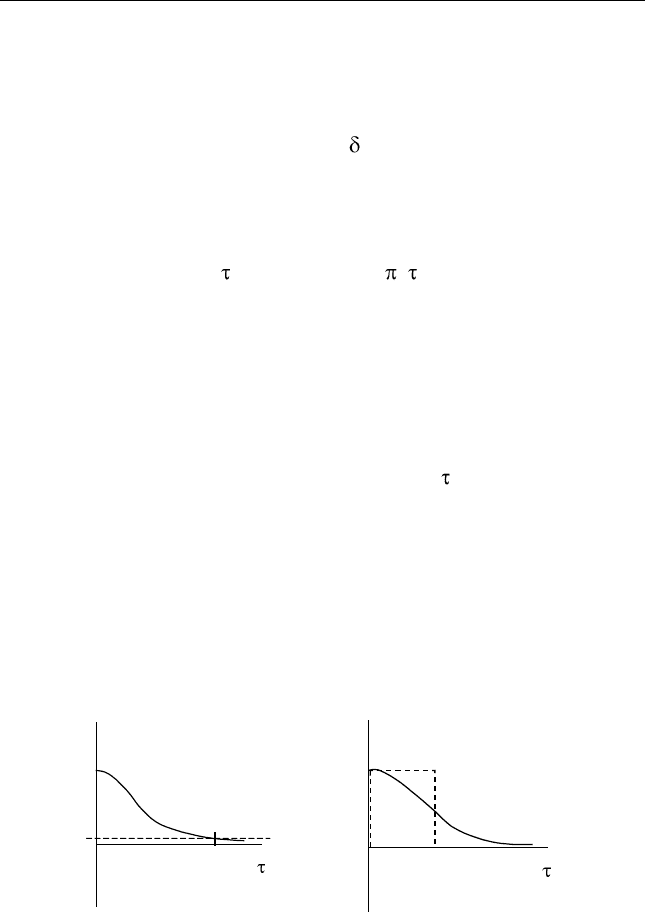
1. Интервал корреляции – такое значение , при котором АКФ

спадает до заданного уровня, например до 1/10 максимального

значения (рис. 3.6, а).

2. Интервал корреляции – основание прямоугольника, имеюще-

го площадь, равную площади под графиком АКФ (рис. 3.6, б).

Эффективную ширину спектра определяют по спектральной

плотности мощности способами, аналогичными показанным на

рис. рис. 3.6, а и 3.6, б.

Очень часто используют следующие две модели стационарных

случайных процессов.

(τ)

а б

Рис. 3.6. К определению интервала корреляции