Васюков В.Н. Теория электрической связи

Подождите немного. Документ загружается.

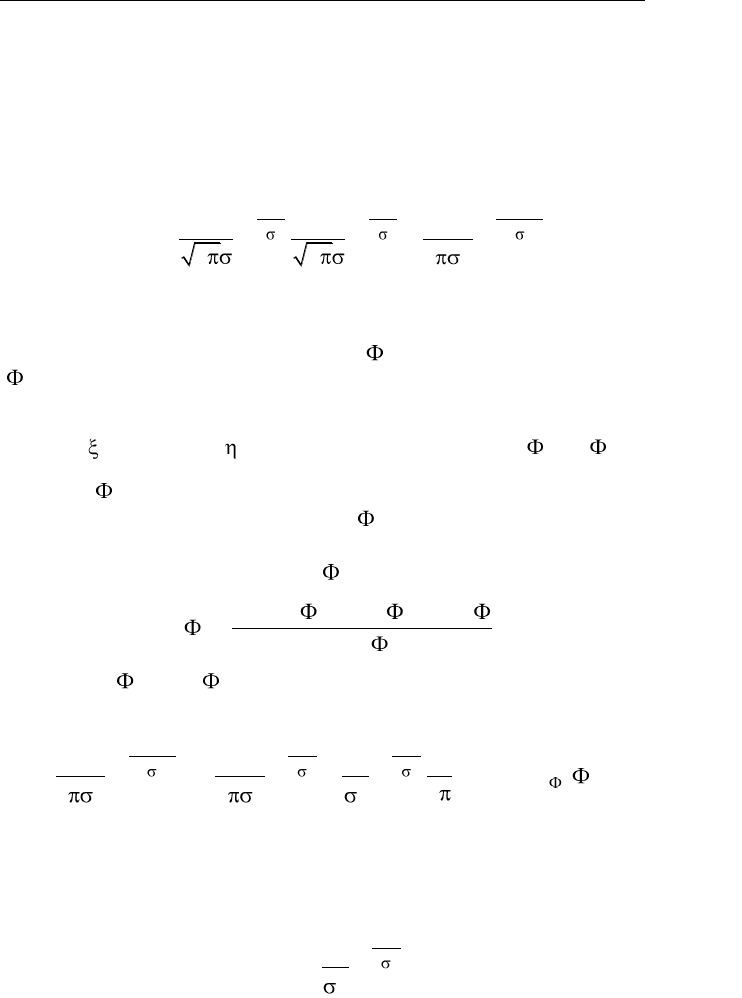
3.6. Узкополосные случайные процессы

133

В совпадающие моменты времени значения процессов

()xt

некоррелированны, а следовательно, в силу гауссовости, и

независимы. Кроме того, они имеют одинаковую дисперсию, по-

этому можно записать совместную плотность распределения веро-

ятностей отсчетов

процессов

()xt

в некоторый мо-

мент времени

2 2 2 2

2 2 2

1 1 1

( , )

x y x y

w x y e e e



  



Рассматривая

как декартовы координаты точки на плос-

кости, введем элементарную площадку

dxdy

, которая в полярных

координатах выражается, как

dA Ad

, где

– длина радиуса,

– угол. Вероятность того, что точка с координатами

по-

падает в элементарную площадку

dxdy

, равна

 

, ( , ) ( , )x x dx y y dy w x y dxdy W A dAd

P        

где

( , )WA

– совместная плотность распределения вероятностей

огибающей

и начальной фазы комплексного случайного

процесса в момент времени

. Исходя из этого очевидного равен-

ства и выражая

через

и , можно записать

 

( , ), ( , )

( , )

w x A y A AdAd

dAd



(здесь

( , ), ( , )x A y A

– обратные функции, описывающие пре-

образование полярных координат в декартовы)

2 2 2 2

2 2 2

( ) ( )

x y A A

e A e e W A W



  

   

Из полученного выражения видно, что огибающая и начальная

фазы в некоторый фиксированный момент времени представляют

собой независимые случайные величины с плотностями распреде-

ления вероятностей

()

W A e





(3.22)

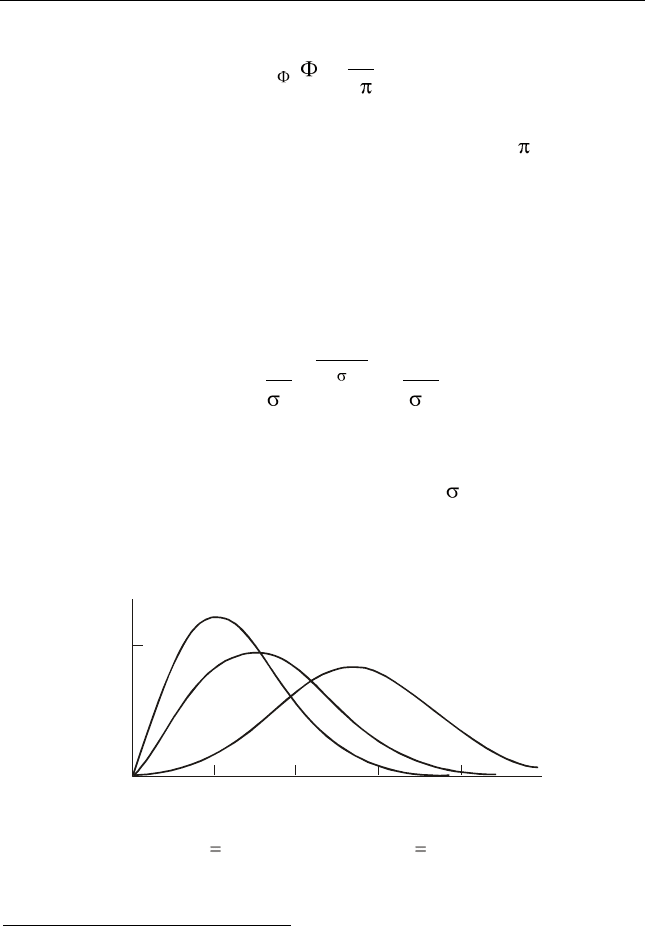
3. СЛУЧАЙНЫЕ ПРОЦЕССЫ

134

()

W 

Плотность (3.22) называется рэлеевской

(рис. 3.10, кривая 1).

Начальная фаза имеет равномерное в интервале

(0,2 )

распреде-

ление. Если случайный процесс имеет ненулевое математическое

ожидание (в задаче анализа помехоустойчивости приема сигнала

на фоне шума это соответствует присутствию полезного сигнала

в принимаемом колебании), то распределение вероятностей оги-

бающей становится более сложным и принимает вид обобщенного

распределения Рэлея, или распределения Рэлея – Райса с плотно-

стью

()

A AU

W A e I













где

– амплитуда сигнала,

()I 

– модифицированная функция

Бесселя нулевого порядка. Плотность обобщенного распределения

Рэлея показана на рис. 3.10, кривые 2, 3 (

1, 1A 

Распределение начальной фазы для этого случая не является

равномерным; его точный вид достаточно сложен и здесь не рас-

сматривается.

()

0,5

0 1 2 3 4

Рис. 3.10. Распределения Рэлея (кривая 1) и Рэлея –

Райса при

1,2U

(кривая 2) и при

2,5U

(кривая 3)

Джон Уильям Стретт, лорд Рэлей (1842 – 1919) – знаменитый англий-

ский физик, известный трудами в области теории колебаний и др.; но-

белевский лауреат 1904 г.

Контрольные вопросы

135

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какое из утверждений правильно: 1) случайная величина –

это число; 2) случайная величина – это функция? Почему?

2. Перечислите свойства функции распределения и плотности

распределения вероятностей случайной величины.

3. Что такое моменты распределения СВ?

4. Как определить энтропию распределения СВ?

5. Может ли дисперсия СВ равняться нулю?

6. Может ли математическое ожидание СВ равняться нулю?

7. Что такое корреляция и как она связана с ковариацией?

8. Что является полным описанием случайного процесса?

9. Что получится, если

-мерную совместную плотность

распределения вероятностей случайного процесса проинтегриро-

вать по

( 1)N 

переменным?

10. Какой процесс называется стационарным в узком смысле?

11. Какой процесс называется стационарным в широком смысле?

12. Утверждение: «Если процесс стационарен в узком смысле,

то он стационарен и в широком смысле» – верно? неверно? верно

для некоторых процессов (каких именно)? неверно для некоторых

процессов (каких именно)?

13. Утверждение: «Если процесс стационарен в широком

смысле, то он стационарен и в узком смысле» – верно? неверно?

верно для некоторых процессов (каких именно)? неверно для неко-

торых процессов (каких именно)?

14. Утверждение: «Если случайные величины независимы, то

они и некоррелированны» – верно? неверно? верно для некоторых

распределений (каких именно)? неверно для некоторых распреде-

лений (каких именно)?

15. Утверждение: «Если случайные величины некоррелирован-

ны, то они и независимы» – верно? неверно? верно для некоторых

распределений (каких именно)? неверно для некоторых распреде-

лений (каких именно)?

16. Какие процессы называются эргодическими?

17. Как связаны АКФ и СПМ стационарного случайного про-

цесса?

18. Что такое белый шум? Какова его АКФ? Какова его СПМ?

19. Как связана СПМ процесса на выходе ЛИС-цепи с СПМ

процесса на входе?

20. Какую ПРВ имеют огибающая и фаза гауссовского узкопо-

лосного случайного процесса?

3. СЛУЧАЙНЫЕ ПРОЦЕССЫ

136

УПРАЖНЕНИЯ

1. Докажите, что процесс, стационарный в узком смысле, стацио-

нарен и в широком смысле.

2. Реализации случайного процесса представляют собой функции

времени

cos( )t 

 

,t   

при некотором фиксированном

значении и случайной начальной фазе , имеющей распределе-

ние, равномерное в интервале

(0,2 )

. Проверьте, является ли этот

процесс стационарным и эргодическим.

3. Мгновенное значение случайного процесса имеет распределе-

ние вероятностей с плотностью вида

( ) exp( 0,5 )w x C x  

. Найди-

те константу

, математическое ожидание и дисперсию. Построй-

те графики плотности распределения вероятностей и функции

распределения вероятностей (друг под другом в одном масштабе).

4. Мгновенное значение случайного процесса описывается функ-

цией распределения

( ) 1 exp( 2 ), 0F x x x   

. Найдите плотность

распределения вероятностей, математическое ожидание, диспер-

сию. Постройте графики плотности распределения вероятностей и

функции распределения вероятностей (друг под другом в одном

масштабе).

5. Функция автокорреляции стационарного случайного процесса

имеет вид

()

B D e





, где

– некоторая постоянная. Найдите

спектральную плотность мощности случайного процесса.

6. Спектральная плотность мощности окрашенного шума

()xt

имеет вид

()

G f Ce





, где

– некоторые постоянные.

Найдите АКФ процесса.

4.1. Метод, основанный на решении дифференциального уравнения

137

4. МЕТОДЫ АНАЛИЗА ЛИС-ЦЕПЕЙ

адача анализа состоит в нахождении выходного

сигнала по заданному входному сигналу и из-

вестному описанию цепи. Не существует метода решения этой за-

дачи, подходящего для всех цепей – линейных и нелинейных, ста-

ционарных и нестационарных. Наиболее хорошо развиты в на-

стоящее время методы анализа линейных инвариантных к сдвигу

цепей. Невыполнение требований линейности и стационарности

(или хотя бы одного из них) приводит к большим трудностям в

решении задачи анализа.

Как было показано в разд. 2, сигнал на выходе ЛИС-цепи мо-

жет быть найден точно, если известно описание цепи в форме им-

пульсной или комплексной частотной характеристики (функцио-

нальное описание [14]). Часто цепь описывается другими

(структурными) способами (принципиальной схемой, дифферен-

циальным уравнением и т.п.). Поскольку любая форма исчерпы-

вающего описания определяет одну и ту же цепь, существует

внутренняя связь между этими формами, и выяснение этой связи

входит в задачу анализа

. В этом смысле все точные методы ана-

лиза эквивалентны друг другу. В основе всякого приближенного

метода лежит какое-нибудь упрощающее предположение, поэтому

такие методы всегда приводят к различным решениям, однако они

должны мало

отличаться от точного решения.

Точными методами анализа ЛИС-цепей являются метод, осно-

ванный на решении дифференциального уравнения цепи, опера-

торный и спектральный методы, метод комплексной огибающей.

Согласно [14] анализ состоит в нахождении функционального описания

цепи по известному ее структурному описанию; нахождение структур-

ного описания по заданному функциональному составляет существо

задачи синтеза.

В каждом конкретном случае нужно определить количественную меру

отличия и количественный критерий малости.

4. МЕТОДЫ АНАЛИЗА ЛИС-ЦЕПЕЙ

138

Они являются точными и универсальными в том смысле, что по-

зволяют в принципе решить задачу анализа точно при любой ЛИС-

цепи и любом воздействии. Однако во многих практически важных

случаях точное решение оказывается слишком трудоемким. В то

же время некоторые дополнительные сведения о сигнале и цепи

могут существенно упростить анализ и привести к результату хотя

и приближенному, но достаточно близкому к точному решению с

практической точки зрения. К приближенным относятся метод

мгновенной частоты (см. п. 5.5.2) и некоторые другие. В этом раз-

деле кратко рассматриваются точные методы анализа ЛИС-цепей.

4.1. МЕТОД, ОСНОВАННЫЙ НА РЕШЕНИИ

ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ

Дифференциальные уравнения вообще связывают значения

некоторых физических величин со скоростями их изменения, ско-

ростями изменения скоростей (ускорениями) и т.д. Эти связи, вы-

раженные в форме дифференциальных уравнений, отражают объ-

ективные физические законы, которым подчиняется реальный мир.

Линейные стационарные цепи с сосредоточенными параметрами

описываются наиболее простыми дифференциальными уравне-

ниями – обыкновенными линейными дифференциальными уравне-

ниями с постоянными коэффициентами

вида

( ) ( )

... ( ) ... ( )

d y t d x t

a a y t b b x t

dt dt

    

, (4.1)

где

()xt

– входной сигнал,

()yt

– выходной сигнал, а целые числа

определяются сложностью цепи. Если входной сигнал за-

дан, то тем самым задана вся правая часть уравнения, которую

можно обозначить

()ft

. Тогда уравнение можно записать в виде

()

... ( ) ( )

d y t

a a y t f t

  

, (4.2)

при этом число

определяет порядок дифференциального уравне-

ния. Знание уравнения, описывающего цепь, а также состояния

цепи

в начальный момент времени (начальных условий) позволя-

Цепи с распределенными параметрами описываются дифференциаль-

ными уравнениями в частных производных.

Состояние цепи определяется набором величин

()yt

( ) /dy t dt

, ...,

( ) /

dy t dt

4.1. Метод, основанный на решении дифференциального уравнения

139

ет найти состояние цепи в любой будущий момент времени (цепь

считается каузальной, т.е. ее поведение не зависит от будущих зна-

чений входного и выходного сигналов). Уравнение (4.2) имеет не-

нулевую правую часть и называется неоднородным; его решение

представляет собой сумму некоторого частного решения неодно-

родного уравнения и общего решения однородного уравнения

()

... ( ) 0

d y t

a a y t

  

. (4.3)

Для решения однородного дифференциального уравнения (4.3)

нужно решить алгебраическое характеристическое уравнение цепи

1 1 0

... 0

a a a a



    

. (4.4)

Если коэффициенты уравнения вещественны (а это практиче-

ски всегда так), то корни либо вещественны, либо образуют ком-

плексно-сопряженные пары. При этом некоторые корни могут сов-

падать (быть кратными). Для случая, когда все корни

, ,...,

являются различными (простыми), общее решение однородного

дифференциального уравнения (4.3) описывает собственные коле-

бания цепи и имеет вид

( ) ...

y t C e C e C e

   

где постоянные

, ,...,

C C C

определяются начальными условиями.

В случае кратных корней в решении присутствуют с соответст-

вующими весовыми коэффициентами слагаемые вида

,...,



, где

– корень уравнения (4.4) кратности

. За-

метим, что для устойчивости цепи свободные колебания должны

затухать со временем, а отсюда следует, что все корни характери-

стического уравнения должны иметь отрицательные вещественные

части (лежать в левой половине комплексной плоскости).

Метод анализа, основанный на решении дифференциального

уравнения, может использоваться для нахождения откликов не-

сложных ЛИС-цепей на простые воздействия (например, функцию

включения, и т.п.). В более сложных случаях этот метод применя-

ется редко.

Пример 4.1. Для RC-фильтра нижних частот (см. пример 2.17),

обозначая ток, протекающий через емкость,

()it

, входное и выходное

4. МЕТОДЫ АНАЛИЗА ЛИС-ЦЕПЕЙ

140

напряжения

вх

()ut

вых

()ut

и учитывая, что

вых

( ) ( )/i t Cdu t dt

запишем неоднородное дифференциальное уравнение

вх вых вых

( ) ( )/ ( )u t RCdu t dt u t

Соответствующее однородное уравнение имеет вид

вых вых

( )/ ( ) 0du t dt u t

, где

RC

– постоянная времени, и ха-

рактеристическое уравнение

10

. Единственный корень ха-

рактеристического уравнения

1/

, и общее решение однород-

ного уравнения, описывающее свободные колебания на выходе

цепи, имеет вид

вых

()

u t Ce





, где

определяется некоторым

частным решением неоднородного уравнения и начальными усло-

виями. Если входное напряжение описывается функцией включе-

ния, частным решением неоднородного уравнения является уста-

новившаяся реакция цепи, равная, очевидно, функции включения.

Тогда решение неоднородного уравнения имеет вид

вых

( ) ( )

u t Ce t





Начальным условием для уравнения является условие

вых

(0) 0u 

, откуда

1C 

, таким образом, отклик цепи на функ-

цию включения, называемый переходной характеристикой, равен

при

( ) 1

g t e





. ◄

4.2. СПЕКТРАЛЬНЫЙ МЕТОД

Предположим, что на вход ЛИС-цепи, описываемой диффе-

ренциальным уравнением (4.1), воздействует комплексное гармо-

ническое колебание вида

()

x t e

, где – круговая частота ко-

лебания. Как было показано в разд. 2, сигнал на выходе ЛИС-цепи

при таком воздействии равен

( ) ( )

y t H e

, где

()H

– значение

КЧХ на частоте . Подставляя

()xt

()yt

в уравнение (4.1) и ре-

шая полученное алгебраическое уравнение относительно

()H

получаем комплексную частотную характеристику, выраженную

через коэффициенты дифференциального уравнения цепи:

   

1 1 0

...

()

...

b j b j b j b

a j a j a j a



   



   

4.3. Операторный метод

141

Таким образом, зная дифференциальное уравнение, описы-

вающее ЛИС-цепь, можно для нахождения выходного сигнала

воспользоваться спектральным методом, для чего найти спек-

тральную плотность

()X

входного сигнала, умножить ее на КЧХ,

а от полученной спектральной плотности

()Y

выходного сигнала

перейти к его временному представлению путем обратного преоб-

разования Фурье.

Пример 4.2. КЧХ фильтра нижних частот, рассмотренного в

примере 4.1, равна, очевидно,

 

( ) 1/ 1H j RC



. Рассматривая в

качестве входного сигнала -функцию со спектральной плотно-

стью, тождественно равной 1, имеем спектральную плотность вы-

ходного сигнала

 

( ) 1/ 1Y j RC



, откуда обратным преобразо-

ванием Фурье находится импульсная характеристка

()

h t e





, равная производной переходной характеристики. ◄

4.3. ОПЕРАТОРНЫЙ МЕТОД

Операторный метод

основан на символической замене опе-

ратора дифференцирования множителем, который принято обозна-

чать буквой

. При этом функции времени

()xt

()yt

должны

быть заменены их изображениями

()Xp

()Yp

, определяемыми

преобразованием

Лапласа

( ) ( )

X p x t e dt









( ) ( )

Y p y t e dt









При таком допущении дифференциальное уравнение (4.1) преобра-

зуется в алгебраическое уравнение

1 0 1 0

( ) ... ( ) ( ) ( ) ... ( ) ( )

a p Y p a pY p a Y p b p X p b pX p b X p      

Операторный метод был в основном разработан Оливером Хевисайдом

(1850 – 1925), выдающимся английским инженером и математиком

(подробнее см., например, [14]).

Это одностороннее преобразование Лапласа определено для функций,

равных нулю при

и растущих при

не быстрее чем

при

[14].

Пьер Симон Лаплас (1749 – 1827) – знаменитый французский матема-

тик, физик и астроном, один из создателей теории вероятностей.

4. МЕТОДЫ АНАЛИЗА ЛИС-ЦЕПЕЙ

142

Вводя операторную передаточную функцию

()Kp

формулой

()



получаем

1 1 0

...

()

...

b p b p b p b

a p a p a p a



   



   

Таким образом, нахождение выходного сигнала ЛИС-цепи опе-

раторным методом сводится к следующим шагам:

переход от входного сигнала

()xt

к его лапласовскому изо-

бражению

()Xp

;

нахождение изображения выходного сигнала

( ) ( ) ( )Y p K p X p

;

переход от изображения

()Yp

к выходному сигналу

()yt

пу-

тем обратного преобразования Лапласа

( ) ( )

y t Y p e dt







где

– константа, которая должна быть больше абсциссы абсо-

лютной сходимости [8].

Легко видеть, что передаточная функция ЛИС-цепи получается

из ее КЧХ путем замены

j p j  

(что соответствует ана-

литическому продолжению функции, заданной на мнимой оси

комплексной плоскости, на всю комплексную плоскость). Верно и

обратное: зная передаточную функцию ЛИС-цепи, путем замены

pj

(сужения функции комплексного переменного на мнимую

ось комплексной

-плоскости) можно получить КЧХ:

( ) ( )H K j

. Учитывая, что для многих функций лапласовские

изображения давно найдены и сведены в таблицы, операторный

метод анализа ЛИС-цепей оказывается во многих случаях самым

простым. Подробное обсуждение операторного метода с много-

численными примерами можно найти в [14].

Пример 4.3. Передаточная функция RC-фильтра нижних частот

равна

1 1/

()

1 1/





, а изображение -функции равно 1.