Васюков В.Н. Теория электрической связи

Подождите немного. Документ загружается.

4.4. Метод комплексной огибающей

143

Перемножая, получим

()





. В таблице преобразований

Лапласа [14] есть изображение

1/( )





. Полагая

1/

получаем отклик на -функцию (импульсную характеристику) ви-

да

()

h t e





. ◄

4.4. МЕТОД КОМПЛЕКСНОЙ ОГИБАЮЩЕЙ

Метод комплексной огибающей обычно применяется для ана-

лиза частотно-избирательных цепей (ЧИЦ) при узкополосных воз-

действиях. Именно эта ситуация имеет место в приемных устрой-

ствах, где модулированные узкополосные колебания воздействуют

на частотно-избирательные ЛИС-цепи (фильтры).

Узкополосный сигнал

()xt

со средней частотой

можно вы-

разить через его комплексную огибающую

()t

следующим обра-

зом (см. разд. 2):

 

( ) Re ( )

j F t

x t t e





( ) ( )

j F t j F t

t e t e

  







поэтому спектральная плотность

()Xf

сигнала

()xt

может быть

записана в виде

   

()

X f f F f F



    



, (4.5)

где

()f

– спектральная плотность комплексной огибающей

()t

Импульсная характеристика

()ht

частотно-избирательной цепи

(полосового фильтра с центральной частотой

), рассматриваемая

как сигнал, также имеет узкополосный характер и может быть

представлена в форме

 

0 0 0

2 2 2

( ) Re ( ) ( ) ( )

j F t j F t j F t

h t t e t e t e

   



  



поэтому КЧХ такой цепи можно записать в виде

   

()

H f f F f F



    



. (4.6)

4. МЕТОДЫ АНАЛИЗА ЛИС-ЦЕПЕЙ

144

Тогда спектральная плотность

()Yf

сигнала

()yt

на выходе

фильтра равна

   

()Y f H f X f

       

0 0 0 0

f F f F f F f F



       



. (4.7)

Здесь учтено то обстоятельство, что функции

 

fF

 

fF

равны нулю при

0f 

, а функции

 

fF

 

fF

при

0f 

Для приведения (4.7) к виду, аналогичному выражениям (4.5),

(4.6), запишем

   

()

Y f f F f F



    



где

()f

– спектральная плотность комплексной огибающей

()t

выходного сигнала

 

0 0 0

2 2 2

( ) Re ( ) ( ) ( )

j F t j F t j F t

y t t e t e t e





  



. (4.8)

Заметим, что при этом

     

f f f

, откуда следует, что

комплексная огибающая выходного сигнала может быть найдена

как свертка

( ) ( ) ( )

t t t

комплексной огибающей

()t

входного сигнала и (комплексной)

импульсной характеристики

()

. Цепь с такой ИХ называется

низкочастотным эквивалентом частотно-избирательной цепи. За-

метим, что с точностью до множителя

импульсная характери-

стика НЧ эквивалента совпадает с комплексной огибающей им-

пульсной характеристики ЧИЦ.

Упражнения

145

Таким образом, для нахождения отклика ЧИЦ на узкополосный

сигнал достаточно вычислить свертку (интеграл Дюамеля) ком-

плексных огибающих входного сигнала и импульсной характери-

стики фильтра, умножить результат на

и затем найти выходной

сигнал согласно выражению (4.8).

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Где должны располагаться корни характеристического урав-

нения устойчивой цепи?

2. Как связана комплексная частотная характеристика ЛИС-

цепи с ее передаточной функцией?

3. Как связаны характеристики частотно-избирательной цепи и

ее низкочастотного эквивалента?

УПРАЖНЕНИЯ

1. Составьте дифференциальное уравнение

-фильтра ниж-

них частот (интегрирующей цепочки). Выведите КЧХ и переда-

точную функцию цепи. Найдите импульсную характеристику.

2. Составьте дифференциальное уравнение

-фильтра верх-

них частот (дифференцирующей цепочки). Выведите КЧХ и пере-

даточную функцию цепи. Найдите импульсную характеристику

цепи.

3. Найдите низкочастотный эквивалент колебательного конту-

ра, если его комплексное сопротивление описывается выражением

()













, где

– сопротивление на резонансной

частоте

– добротность контура.

5. ПРИНЦИПЫ МОДУЛЯЦИИ И ДЕМОДУЛЯЦИИ

146

5. ПРИНЦИПЫ МОДУЛЯЦИИ

И ДЕМОДУЛЯЦИИ

одуляция – это изменение одного или не-

скольких параметров колебания, называемо-

го несущим колебанием (переносчиком), в соответствии с измене-

ниями первичного (информационного) сигнала. При этом спектр

(спектральная плотность) получаемого модулированного сигнала

отличается от спектров как первичного сигнала, так и переносчика.

Можно сказать, что такое изменение спектра является целью моду-

ляции: например, речевой сигнал в системах телефонии занимает

полосу частот от 300 до 3400 Гц и его непосредственная передача

по каналу радиосвязи невозможна, так как размеры антенны, эф-

фективно излучающей радиоволны столь низких частот, были бы

слишком велики для практического применения. В результате ам-

плитудной модуляции таким сигналом гармонического несущего

колебания с частотой, например, 1 МГц получается амплитудно-

модулированный (АМ) сигнал, занимающий полосу частот от

996 600 до 1 003 400 Гц, излучение которого не составляет проблемы.

Важно отметить, что при модуляции (а также демодуляции)

происходят такие преобразования первичного сигнала, которые

сопровождаются появлением новых частотных составляющих, от-

сутствовавших в спектре исходного сигнала. Практически во всех

случаях после такого обогащения спектра (ОС) производится час-

тотная фильтрация (ЧФ) при помощи подходящей ЛИС-цепи для

подавления ненужных или вредных спектральных составляющих,

(рис. 5.1). При помощи одних только ЛИС-цепей модуляцию осу-

ществить невозможно. То же относится к демодуляции

Специальный случай демодуляции ЛИС-цепью будет особо рассмотрен

позднее (разд. 5.7).

5.1. Воздействие гармонического колебания на параметрическую цепь

147

ОС

ЧФ

x(t)

y(t)

Рис. 5.1. Принцип преобразования спектра

колебания

Действительно, предположим, что на вход ЛИС-цепи поступает

периодический сигнал

()

j kt

x t C e









. Действие ЛИС-цепи на

комплексную экспоненту сводится к ее умножению на комплекс-

ное число, равное значению КЧХ цепи на частоте данной экспо-

ненты. Ясно, что спектральные составляющие исходного сигнала

могут исчезать в результате такой фильтрации, но не появляться,

если их изначально не было. Очевидно, что и для непериодических

сигналов справедливо то же самое. Обогащение спектра сигнала

новыми частотами возможно при использовании нелинейных или

линейных нестационарных (параметрических) цепей. Напомним,

что нелинейными называются цепи, для которых не выполняется

принцип суперпозиции. Для линейных нестационарных цепей ука-

занный принцип выполняется, однако оператор цепи зависит от

времени, вследствие чего в спектре сигнала могут появляться но-

вые частоты.

5.1. ВОЗДЕЙСТВИЕ

ГАРМОНИЧЕСКОГО КОЛЕБАНИЯ

НА ПАРАМЕТРИЧЕСКУЮ ЦЕПЬ

Простейшая линейная параметрическая цепь, которую можно

использовать для обогащения спектра, представляет собой актив-

ное сопротивление, меняющееся во времени по некоторому перио-

дическому закону. Удобнее в качестве изменяющегося параметра

рассмотреть переменную проводимость

()st

, так что под воздейст-

вием напряжения

()ut

через параметрический элемент протекает

ток

( ) ( ) ( )i t u t s t

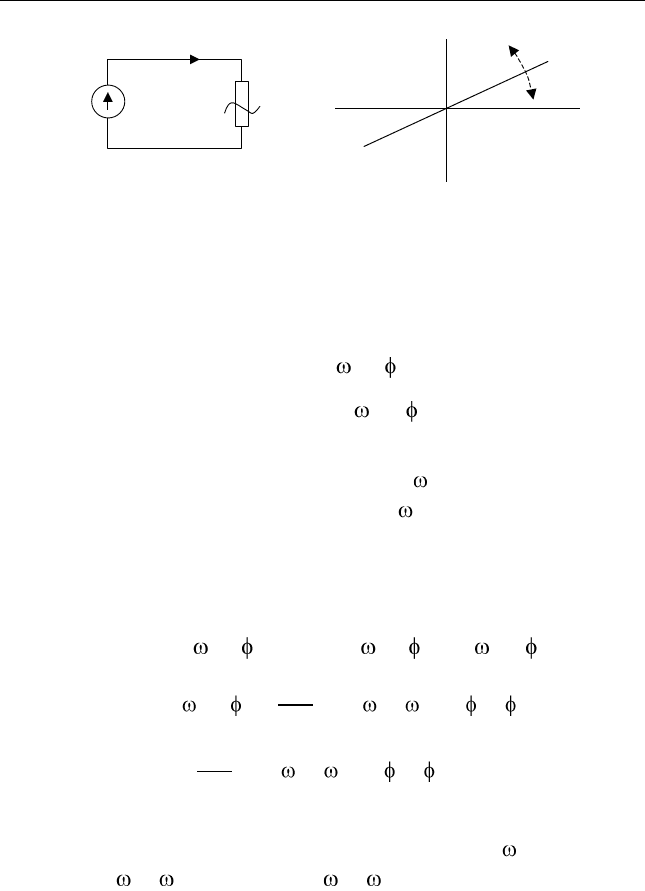
(рис. 5.2, а). Проводимость

()st

можно тракто-

вать, как переменную крутизну линейной вольт-амперной характе-

ристики параметрического элемента (рис. 5.2, б).

5. ПРИНЦИПЫ МОДУЛЯЦИИ И ДЕМОДУЛЯЦИИ

148

()it

()st

()ut

а б

Рис. 5.2. Воздействие переменного напряжения на линейный

параметрический элемент

Рассмотрим простейшую ситуацию, когда напряжение и кру-

тизна изменяются по гармоническому закону с разными частотами

( ) cos( )u t U t

0 1 2 2

( ) cos( )s t S S t  

Очевидно, спектр напряжения содержит одну гармоническую

составляющую (гармонику) с частотой

, а спектр функции

()st

– две составляющие с частотами 0 и

Ток, протекающий через параметрический элемент, равен сум-

ме гармонических составляющих (гармоник), амплитуды и началь-

ные фазы которых образуют соответственно амплитудный и фазо-

вый спектры:

0 1 1 1 1 1 2 2

( ) cos( ) cos( )cos( )i t US t US t t     

 

0 1 1 1 2 1 2

cos( ) cos ( )

US t t      

 

1 2 1 2

cos ( )

t   

. (5.1)

Как видно из полученного выражения, в спектре тока присут-

ствуют гармонические составляющие с частотой

, а также с

суммарной



и разностной



частотами. Очевидно, что

при более сложном спектральном составе напряжения и/или кру-

тизны количество новых частот будет больше (в любом случае

спектральные коэффициенты можно найти по тригонометрическим

формулам, раскрывая произведения косинусов и/или синусов).

5.2. Нелинейные элементы и их аппроксимации

149

Наличие в спектре колебания составляющих с суммарной и

разностной частотами позволяет использовать параметрические

цепи для переноса спектра. В самом деле, подавая ток, описывае-

мый выражением (5.1), на частотно-избирательную нагрузку (по-

лосовой фильтр), получим напряжение частоты



или



, в зависимости от настройки фильтра. Таким образом, по-

лучаем перенос частоты

на величину

вправо или влево по

частотной оси.

На практике сигнал, подлежащий преобразованию, имеет

спектр конечной ширины; после умножения сигнала на

()st

при

помощи фильтра выделяется спектр такой же формы, но сдвину-

тый по частоте на

вверх или вниз. Частными случаями перено-

са спектра являются преобразование частоты, применяемое при

супергетеродинном приеме (см. пример 5.1), а также амплитудная

модуляция и синхронное детектирование АМ-сигналов.

5.2. НЕЛИНЕЙНЫЕ ЭЛЕМЕНТЫ

И ИХ АППРОКСИМАЦИИ

К нелинейным элементам, наиболее широко применяемым в

технике генерирования и обработки сигналов, относятся в первую

очередь полупроводниковые приборы (диоды, транзисторы и т.п.),

которые описываются характеристиками (чаще всего рассматри-

ваются вольт-амперные характеристики – ВАХ), имеющими весь-

ма сложный вид. Для целей анализа эти характеристики аппрокси-

мируют математическими зависимостями, которые должны быть

достаточно простыми и в то же время сохранять существенные

черты аппроксимируемых характеристик. Рассмотрим наиболее

часто применяемые аппроксимации.

5.2.1. ПОЛИНОМИАЛЬНАЯ (СТЕПЕННАЯ)

АППРОКСИМАЦИЯ

Характеристика нелинейного элемента (НЭ) представляется

полиномом [13] некоторой степени

0 1 2

( ) ...

i f u a u a a u a u a u



     



. (5.2)

Во всех практических случаях функция

()fu

аппроксимирует

истинную ВАХ (заданную графически или таблично) не на всей

5. ПРИНЦИПЫ МОДУЛЯЦИИ И ДЕМОДУЛЯЦИИ

150

числовой оси, а только на некотором ограниченном интервале зна-

чений независимой переменной, или рабочем участке. Выберем на

этом участке

1N 

точек, обозначив их

1 2 1

, ,...,

u u u



. Для каждого

из этих значений напряжения обозначим соответствующие значе-

ния тока (взятые из таблицы или найденные по заданному графику

ВАХ), как

1 2 1

, ,...,

i i i



. Тогда согласно (5.2) можно составить

1N 

уравнение

0 1 1 2 1 1 1

0 1 2 2 2 2 2

0 1 1 2 1 1 1

... ,

...... ...... ...... ...... ...... ,

...

N N N N N

a a u a u a u i

   



   



   







   



1N 

неизвестными

, ,...,

a a a

. Решив эту линейную систему

уравнений, можно найти полиномиальную функцию (5.2).

Во многих реальных задачах удобно рассматривать четную и

нечетную части характеристики. Любую нелинейную характери-

стику можно, очевидно, представить в виде суммы четной и нечет-

ной функций

чн

( ) ( ) ( )f u f u f u

, (5.3)

где четная и нечетная части удовлетворяют следующим выражени-

ям:

чч

( ) ( )f u f u

, (5.4)

нн

( ) ( )f u f u  

. (5.5)

Из выражения (5.3) с учетом (5.4), (5.5) следует

чн

( ) ( ) ( )f u f u f u  

, (5.6)

откуда, складывая и вычитая выражения (5.3) и (5.6), получаем

( ) ( )

()

f u f u





, (5.7)

( ) ( )

()

f u f u





. (5.8)

Пример функции

()Fu

и ее четной и нечетной частей приведен

на рис. 5.3.

5.2. Нелинейные элементы и их аппроксимации

151

Очевидно, при полиномиаль-

ной аппроксимации ВАХ ее чет-

ная и нечетная части складывают-

ся из четных и нечетных

степеней:

ч 0 2 4

( ) ...f u a a u a u  

н 1 3 5

( ) ...f u a u a u a u  

Выделение четной и нечетной

частей ВАХ полезно, когда работа

рассматриваемого устройства оп-

ределяется либо только четной, либо только нечетной частью. На-

пример, при амплитудной модуляции полезная составляющая ко-

лебания определяется только четной частью ВАХ (см. разд. 5.4.2).

Тогда аппроксимацию можно проводить только для четной части,

предварительно выделив ее графически или по таблице значений,

при этом расчет коэффициентов аппроксимации требует решения

системы уравнений меньшего порядка. Кроме того, вид нужной

(четной или нечетной) части ВАХ позволяет оценить «на глаз»

пригодность данного НЭ для реализации требуемого преобразова-

ния сигналов.

Важность выделения четной и нечетной частей ВАХ не огра-

ничивается только теоретическим рассмотрением, так как сущест-

вуют схемные решения, позволяющие получать четные или нечет-

ные характеристики нелинейных цепей путем согласного или

встречного включения одинаковых нелинейных элементов. Так

строятся, например, балансные, мостовые и кольцевые схемы.

Для реализации четной характеристики необходимо использо-

вать два НЭ с одинаковыми ВАХ. Пусть ВАХ каждого элемента

НЭ1

НЭ2

–

НЭ1

НЭ2

–

а б

Рис. 5.4. Балансные схемы

Рис. 5.3. Нелинейная функция

и ее четная и нечетная части

5. ПРИНЦИПЫ МОДУЛЯЦИИ И ДЕМОДУЛЯЦИИ

152

имеет вид

()i F u

. Четную суммарную характеристику можно

получить в соответствии с (5.7) в виде

( ) ( )i F u F u  

Это означает, что необходимо сложить токи двух НЭ, на которые

входное напряжение подается с противоположными знаками (про-

тивофазно), что реализуется в схеме, показанной на рис. 5.4, а, пу-

тем соответствующего подключения вторичной обмотки транс-

форматора к нелинейным элементам. Сложение токов происходит

в общем для них сопротивлении нагрузки.

Реализация нечетной ВАХ осуществляется схемой рис. 5.4, б за

счет вычитания (противофазного сложения) на нагрузке напряже-

ний, создаваемых токами различных НЭ.

( ) ( )i F u F u  

что соответствует выражению (5.8).

Если на нелинейный элемент подается сигнал в сумме с посто-

янным напряжением смещения

, определяющим рабочую точку

ВАХ, удобно аппроксимирующий полином (5.2) представить в

форме

0 1 0 2 0 0

' ' ( ) ' ( ) ... ' ( )

i a a u U a u U a u U      

, (5.9)

где коэффициенты, разумеется, отличаются от коэффициентов

,...,

; при этом упрощаются математические операции при на-

хождении спектра тока.

5.2.2. ЭКСПОНЕНЦИАЛЬНАЯ АППРОКСИМАЦИЯ

Критерием выбора аппроксимирующей функции является

простота аналитического выражения при приемлемой точности

аппроксимации. Вольт-амперные характеристики некоторых нели-

нейных элементов с хорошей точностью представляются экспо-

ненциальными функциями вида

()

i f u Ae

, (5.10)

где

и – константы.