Васюков В.Н. Теория электрической связи

Подождите немного. Документ загружается.

5.4. Амплитудная модуляция гармонического переносчика

173

кажениями. Нелинейные искажения принято характеризовать ко-

эффициентом нелинейных искажений

222

2 3 4

...III





где

– амплитуда

-й гармоники тока. В данном случае

  

%. Такой уровень нелинейных искажений в

большинстве практических приложений (в частности, в радиове-

щании) совершенно недопустим. Заметим, что реальные ВАХ по-

лупроводниковых приборов могут быть аппроксимированы квад-

ратичным полиномом лишь в пределах небольшого участка (при

малом сигнале).

При сильном сигнале более подходящей является кусочно-

линейная аппроксимация (см. п. 5.2.3). Рассмотрим детектор на

биполярном транзисторе, принципиальная схема которого показа-

на на рис. 5.18.

Полагая, что зависимость тока коллектора от напряжения ба-

за – эмиттер аппроксимируется кусочно-линейной функцией

нн

0 при ,

()

( ) при ,

S u U u U













и что напряжение смещения

равно напряжению начала линей-

ного участка характеристики

, видим, что угол отсечки со-

гласно (5.13) равен 90 , тогда при воздействии на вход схемы на-

пряжения АМ-сигнала (5.19) ток коллектора имеет вид импульсов

()ut

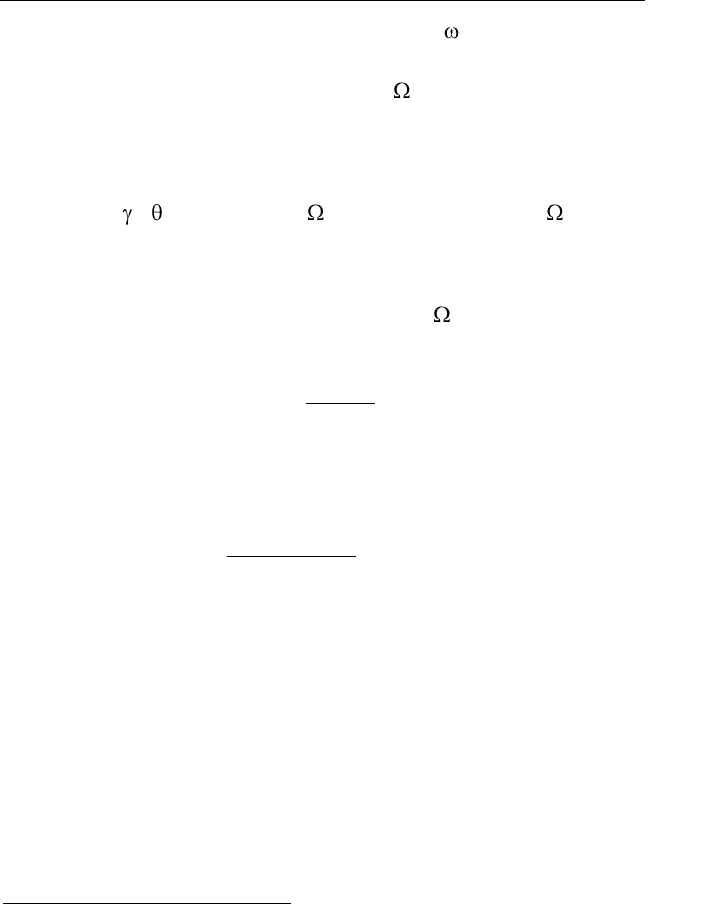
Рис. 5.18. Детектор на биполярном

транзисторе

5. ПРИНЦИПЫ МОДУЛЯЦИИ И ДЕМОДУЛЯЦИИ

174

гармонической формы с частотой следования

, скважностью 2 и

амплитудой

 

1 cos

I SU M t



меняющейся медленно (по закону модулирующего сигнала).

Постоянная составляющая

импульсного тока также медленно

меняется

   

( ) ( ) 1 cos 0.318 1 cos

I t SU M t SU M t   

Таким образом, низкочастотная составляющая выходного на-

пряжения транзисторного детектора

 

( ) 0.318 1 cos

u t SU R M t

. (5.35)

Детекторы характеризуются коэффициентом детектирования

вых

вх



где

выхm

вхm

– амплитуды низкочастотной составляющей вы-

ходного напряжения и несущего колебания соответственно. В дан-

ном случае

0.318

SU RM

k SR



Низкочастотная составляющая выходного напряжения прямо

пропорциональна модулирующему колебанию, т.е. нелинейные

искажения отсутствуют (если пренебречь отличиями реальной ха-

рактеристики от кусочно-линейной). Отметим, что если

0 н

UU

угол отсечки будет зависеть от времени и появятся нелинейные

искажения.

Наиболее простое устройство для детектирования АМ-коле-

баний – диодный детектор (рис. 5.19).

В этой схеме в отличие от транзисторного детектора угол от-

сечки определяется не внешним источником напряжения смеще-

ния, а выходным постоянным

напряжением, приложенным к дио-

ду в обратном направлении. В самом деле, ток, протекающий через

На самом деле это не постоянная, а низкочастотная составляющая сиг-

нала, но для каждого отдельного импульса тока она находится как по-

стоянная составляющая тока на протяжении одного периода.

См. предыдущую сноску.

5.4. Амплитудная модуляция гармонического переносчика

175

АМ

()ut

Рис. 5.19. Диодный детектор

диод в прямом направлении, заряжает конденсатор до некоторого

напряжения, полярность которого такова, что оно стремится «запе-

реть» диод. В результате открытое или запертое состояние диода в

каждый момент времени определяется разностью

()ut

входного

напряжения

()ut

и выходного напряжения

()ut

, показанной

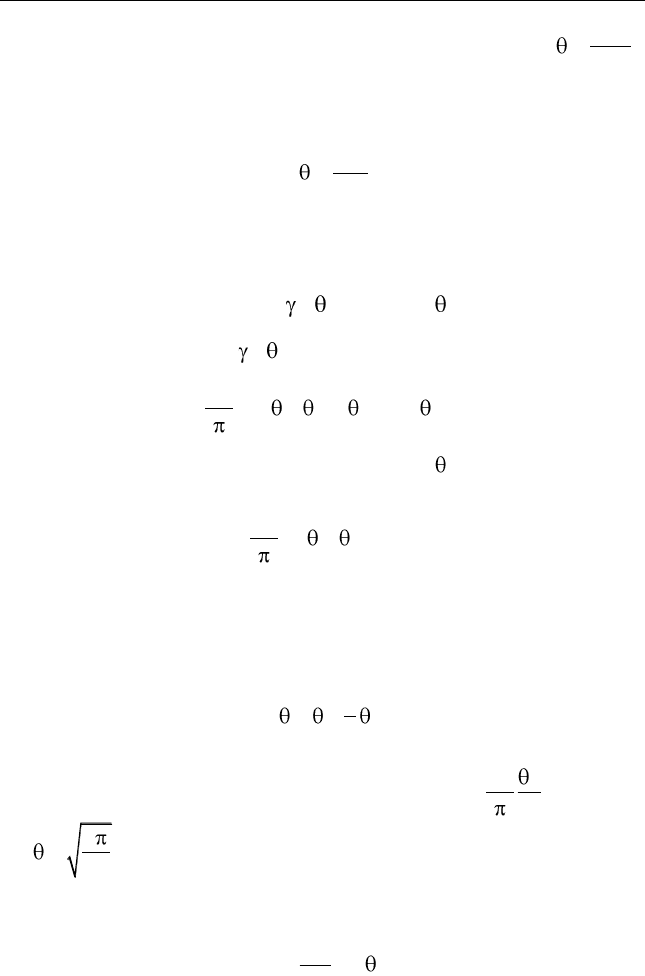
сплошной линией на графике рис. 5.20. Медленно меняющееся вы-

ходное напряжение показано пунктирной линией.

Согласно формуле (5.13)

н0

cos





Рис. 5.20. Диаграммы напряжений и тока в схеме диодного

детектора

5. ПРИНЦИПЫ МОДУЛЯЦИИ И ДЕМОДУЛЯЦИИ

176

а параметр аппроксимации

равен нулю, поэтому

cos





но смещение в данном случае – это напряжение на нагрузке детек-

тора, равное

U I R

, откуда

cos



. (5.36)

Учитывая это уравнение и выражая

через функцию Берга,

запишем

( ) cos

I R SU R U

Раскрывая функцию

()

и сокращая

, получим

 

sin cos cos



откуда, поделив обе части уравнения на

cos

, будем иметь урав-

нение

(tg ) 1



. (5.37)

Заметим, что в это уравнение не входит

. Это означает, что

в линейном детекторе угол отсечки есть величина постоянная, за-

висящая только от параметров схемы. Используем разложение тан-

генса в степенной ряд, ограниченное двумя слагаемыми [8]



Тогда из выражения (5.37) получается уравнение



, отку-

да



Полезная составляющая тока нагрузки, как следует из формулы

(5.36),

cos



5.5. Угловая модуляция

177

пропорциональна

, что и означает линейность детекторной ха-

рактеристики

. Коэффициент детектирования, очевидно, равен

 

cos cos 3 /( )k SR



Практическое применение диодного детектора предполагает

правильный выбор параметров ФНЧ. Необходимо, во-первых, чтобы

сопротивление нагрузки было много больше внутреннего сопротив-

ления диода (в прямом направлении). Это обеспечивает при быст-

ром заряде конденсатора сравнительно медленный его разряд, что

приводит к выделению огибающей АМ-сигнала. Во-вторых, емкость

конденсатора должна выбираться из того условия, чтобы граничная

частота ФНЧ была больше верхней частоты полезного сигнала и в

то же время меньше несущей частоты. Поскольку используемый

ФНЧ первого порядка имеет очень пологую АЧХ, постоянная вре-

мени

-цепи должна удовлетворять двойному неравенству

RC

Нарушение левой части неравенства приводит к слишком бы-

строму разряду конденсатора (напряжение на нагрузке пульсирует

с частотой

), нарушение правой части – к слишком медленному

разряду, вследствие чего напряжение на нагрузке может «не успе-

вать» за более быстрыми изменениями огибающей АМ-сигнала.

При этом форма выделяемой огибающей сильно отличается от мо-

дулирующего сигнала, что соответствует нелинейным искажениям.

5.5. УГЛОВАЯ МОДУЛЯЦИЯ

5.5.1. ОПИСАНИЕ УМ-КОЛЕБАНИЙ

При угловой модуляции гармонического колебания резуль-

тирующий сигнал имеет постоянную амплитуду и зависящую от

первичного (информационного) сигнала фазу, поэтому его можно

записать в общем виде, как

 

УМ 0

( ) cos ( ) cos ( )

u t U t U t t  

, (5.38)

где

()t

– фаза колебания, а

()t

– его начальная фаза.

Диодный детектор можно считать линейным только при сильном сиг-

нале, когда ВАХ диода удовлетворительно аппроксимируется кусочно-

линейной функцией.

5. ПРИНЦИПЫ МОДУЛЯЦИИ И ДЕМОДУЛЯЦИИ

178

Для описания УМ-колебаний полезно ввести понятие мгновен-

ной частоты

( ) ( )

()

d t d t

dt dt

  

. (5.39)

Очевидно, при неизменной начальной фазе мгновенная частота

равна частоте несущего колебания, однако изменение начальной

фазы приводит к изменению мгновенной частоты. При фазовой

модуляции (ФМ) начальная фаза меняется по закону первичного

сигнала, следовательно, мгновенная частота меняется по закону

его производной. При частотной модуляции (ЧМ) в соответствии с

первичным сигналом меняется мгновенная частота, значит, на-

чальная фаза меняется как интеграл первичного сигнала. В любом

случае при угловой модуляции по виду модулированного сигнала

невозможно определить вид модуляции (ЧМ или ФМ), если не из-

вестен закон модуляции.

Пусть частота модулируется по гармоническому закону

0 д

( ) costt



(5.40)

(максимальное отклонение мгновенной частоты от среднего значе-

ния называется девиацией

частоты

). Тогда фаза модулирован-

ного колебания

0 0 0

( ) ( ) sin

t t dt t t    



(5.41)

состоит из линейно меняющегося слагаемого

, постоянной

и гармонического слагаемого, амплитудное значение которого на-

зывается индексом модуляции

(или девиацией фазы), численно

равным при тональной модуляции

m 

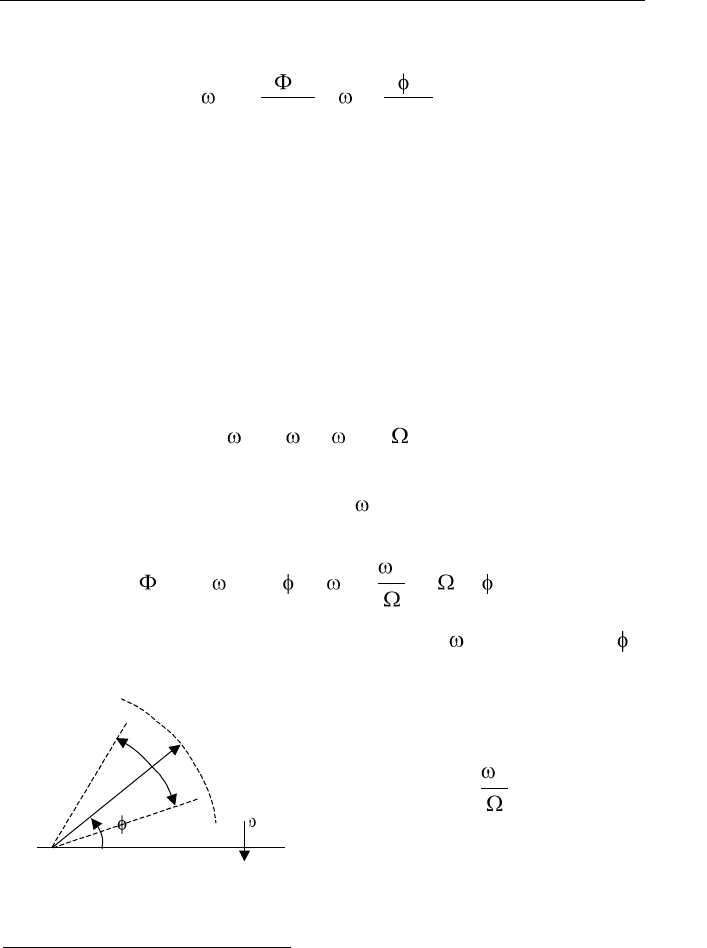
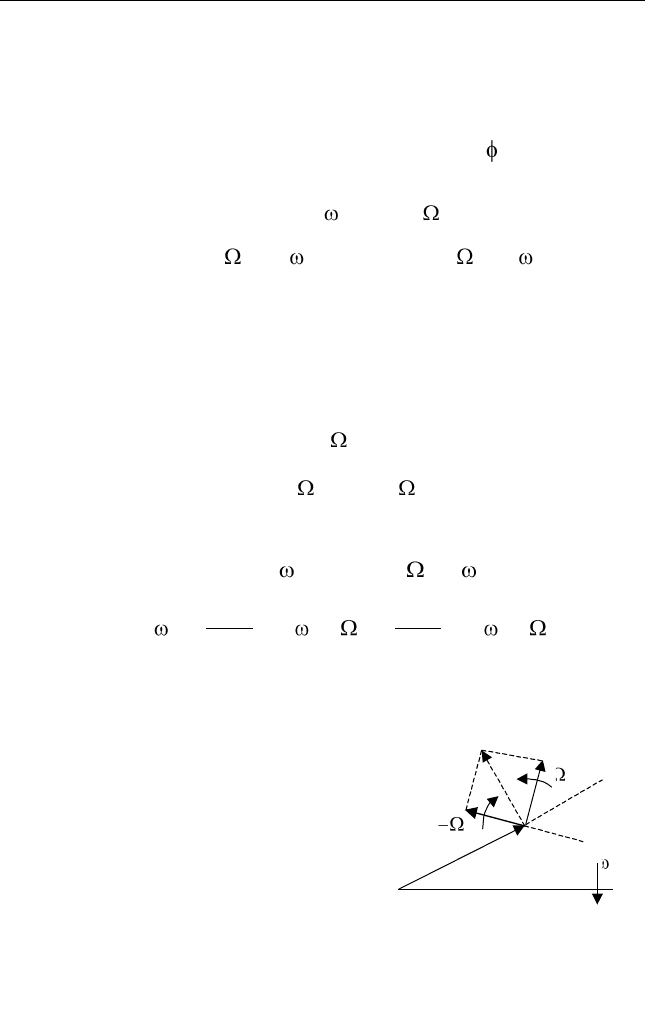
На рис. 5.21 показана вектор-

ная диаграмма УМ-колебания.

Вектор, изображающий колеба-

ние, не изменяет своей длины, но

От англ. deviation – отклонение.

Индекс модуляции, очевидно, имеет размерность радиан.

()t

Рис. 5.21. Векторная диаграмма

колебания с угловой модуляцией

5.5. Угловая модуляция

179

с течением времени он изменяет свое положение между двумя

штриховыми линиями, отстоящими от среднего положения на ве-

личину индекса модуляции, при этом конец вектора перемещается

по окружности.

Рассмотрим спектр колебания с угловой модуляцией по гармо-

ническому закону. Для простоты будем считать

0

. Примем,

что фаза модулируется по синусоидальному закону:

 

УМ 0

( ) cos sin

u t U t m t  

   

cos sin cos sin sin sin

U m t t U m t t

. (5.42)

Заметим, что закон модуляции подвергается нелинейным пре-

образованиям

cos( )

sin( )

, а это должно приводить к обогаще-

нию спектра.

Вначале рассмотрим частный случай малого индекса модуля-

ции

1m 

. Тогда

 

cos sin 1mt



; (5.43)

 

sin sin sinm t m t



. (5.44)

С учетом этих приближенных равенств перепишем (5.42) в виде

УМ 0 0

( ) cos sin sin

u t U t U m t t  

   

0 0 0

cos cos cos

U m U m

U t t t

    

Полученное выражение похоже на выражение (5.20) для АМ-

колебания. Однако отличие в знаке последнего слагаемого приво-

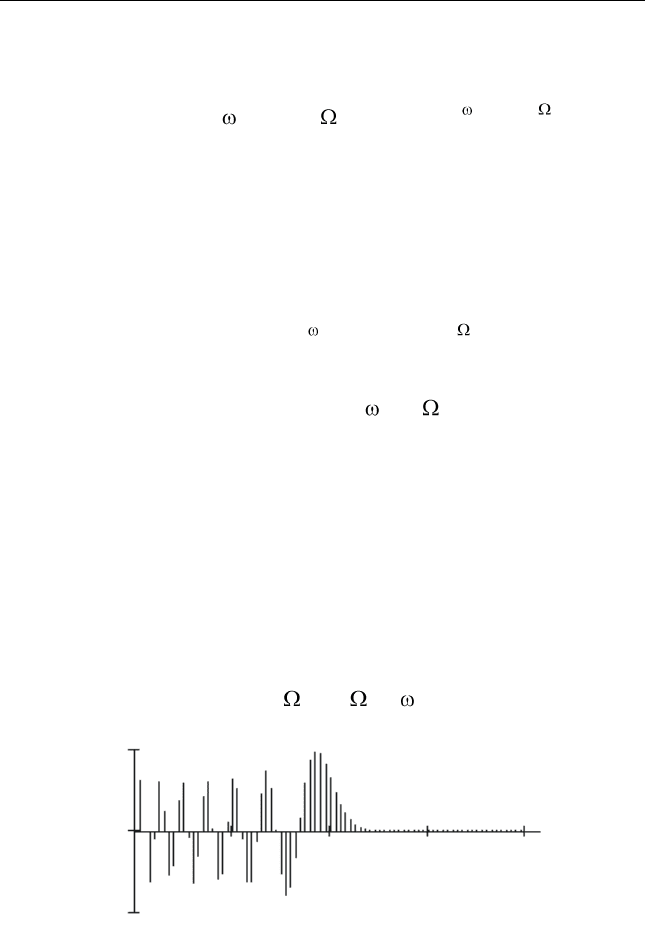
дит к тому, что суммарный вектор

колебания с течением времени из-

меняет свое угловое положение

(рис. 5.22). При этом, очевидно, ко-

нец вектора суммарного колебания

движется по прямой. Это отличие

от идеального УМ-колебания явля-

ется следствием использования

приближенных выражений (5.43),

(5.44). Если

1m 

, то прямая мало

отличается от окружности (тем

меньше, чем меньше

Рис. 5.22. Векторная диаграм-

ма колебания при тональной

УМ с малым индексом

5. ПРИНЦИПЫ МОДУЛЯЦИИ И ДЕМОДУЛЯЦИИ

180

Рассмотренный пример представляет лишь иллюстративный

интерес, так как на практике используются УМ-колебания с боль-

шим индексом. Запишем УМ-колебание в виде

 

УМ 0

( ) cos sin

u t U t m t  

 

sin

jm t

U e e

Известна формула

sin

()

jm x jkx

e J m e









где

()

J 

– функция Бесселя первого рода

-го порядка. С учетом

этого равенства

УМ

( ) Re ( )

jk t

u t U e J m e















 

( )cos

U J m k t









Таким образом, даже при тональной модуляции спектр УМ-

колебания имеет бесконечно много составляющих, амплитуды ко-

торых определяются значениями функции Бесселя

()

, рас-

сматриваемой как функция номера гармоники

при заданном

значении

На рис. 5.23 изображены значения

()

при

40m 

. Видно,

что при

km

они быстро убывают. Благодаря такому поведению

функции Бесселя можно считать, что УМ-колебание имеет спектр с

эффективной шириной, равной

2( 1) 2 2mm

  

0,2

–0,2

0 20 40 60 80

Рис. 5.23. Значения функций Бесселя при различных

k и при

40m 

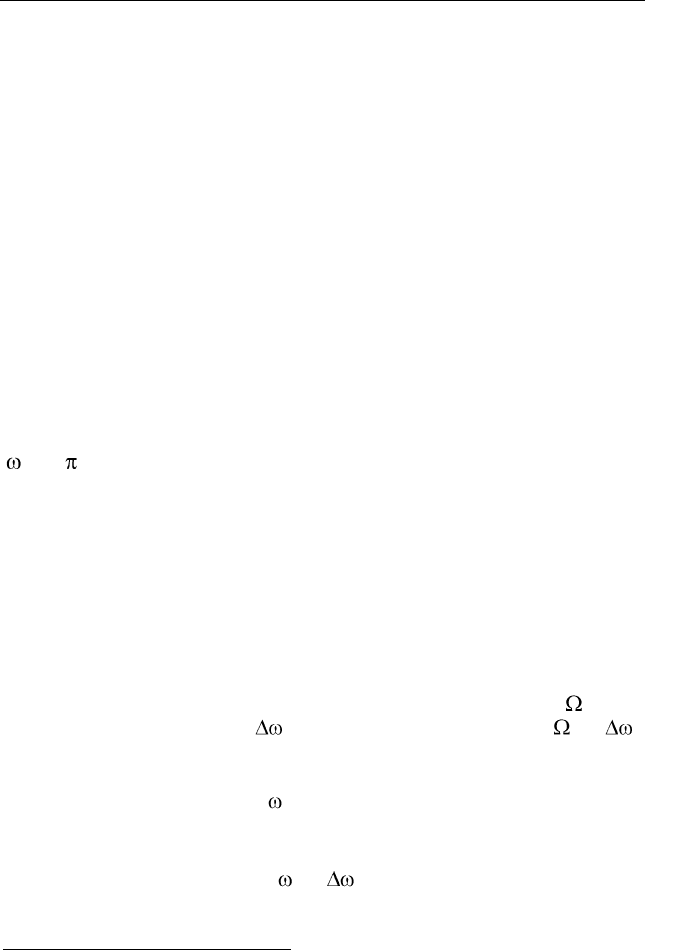
5.5. Угловая модуляция

181

Таким образом, можно в первом приближении считать, что ши-

рина спектра УМ-сигнала равна диапазону изменения частоты при

модуляции, равному удвоенной девиации частоты.

5.5.2. ПРИБЛИЖЕННЫЙ АНАЛИЗ ВОЗДЕЙСТВИЯ

УМ-КОЛЕБАНИЙ НА ЛИС-ЦЕПИ

Сигналы с угловой модуляцией применяются в технике связи

очень широко. При этом часто представляет большой практиче-

ский интерес задача анализа колебаний на выходе ЛИС-цепи

(фильтра, линейного стационарного канала связи) при воздействии

УМ-колебания. При негармоническом первичном сигнале и боль-

шом индексе модуляции точный анализ методами, рассмотренны-

ми в разд. 4, практически невозможен. Поэтому для приближенно-

го анализа прохождения сигналов с угловой модуляцией через

частотно-избирательные цепи применяется метод мгновенной час-

тоты.

При угловой модуляции несущего колебания с частотой

2 f

и амплитудой

низкочастотным колебанием (первич-

ным сигналом)

()bt

получается сигнал, который можно прибли-

женно рассматривать как «гармоническое колебание с медленно

меняющейся частотой»

. Под частотой здесь понимается мгновен-

ная частота УМ-колебания, а ее изменения могут считаться мед-

ленными, если мгновенные частоты УМ-колебания и отклика на

него частотно-избирательной цепи практически совпадают. Для

этого, очевидно, требуется, чтобы скорость протекания переход-

ных процессов в ЧИЦ была велика в сравнении со скоростью из-

менения модулирующего сигнала. Отсюда вытекает требование,

чтобы верхняя частота спектра модулирующего сигнала была

намного меньше ширины полосы пропускания цепи



Однако скорость изменения мгновенной частоты УМ-сигнала за-

висит также от амплитуды модулирующего сигнала, которая опре-

деляет девиацию частоты

– максимальное отклонение мгно-

венной частоты от среднего значения [см. (5.40)]. Принято считать

[23], что для применения метода мгновенной частоты достаточно,

чтобы выполнялось условие



Разумеется, в строгом смысле такое колебание не является гармониче-

ским и имеет сложный спектр, рассмотренный в разд. 5.5.1.

5. ПРИНЦИПЫ МОДУЛЯЦИИ И ДЕМОДУЛЯЦИИ

182

Перепишем (5.38) в виде

 

 

 

()

УМ

( ) cos ( ) Re Re

j t t

m m m

u t U t U e U e



  

Тогда колебание на выходе ЛИС-цепи с комплексной частотной

характеристикой

()

( ) ( )

H K e

имеет вид

 

 

( ) ( )

вых

( ) ( ( ))Re

j t t t

u t U K t e









 

( ( ))cos ( ) ( )

U K t t t t



  



откуда видно, что выходной сигнал имеет переменную амплитуду

( ( ))

U K t

, меняющуюся по закону, зависящему от изменений

мгновенной частоты входного сигнала (происходит паразитная

амплитудная модуляция). Закон изменения начальной фазы вы-

ходного сигнала также отличается от начальной фазы входного

сигнала на величину, зависящую от времени и определяемую из-

менениями мгновенной частоты входного сигнала

()t

и фазоча-

стотной характеристикой цепи

()

. Таким образом, ЛИС-цепь

вносит искажения и в закон угловой модуляции сигнала. Мгновен-

ная частота выходного сигнала отличается от мгновенной частоты

входного сигнала (5.39) и равна

 

вых 0

()

dt dt

  

Пример 5.1. На колебательный контур, настроенный на часто-

ту несущего колебания, поступает УМ-сигнал с мгновенной часто-

той, определяемой выражением (5.40)

0 д

( ) costt



Тогда мгновенная частота выходного сигнала

 

вых 0

()

dt dt

   

 

0 д 0 д

cos cos



   



где

 

0 д

( ) cos







– периодическая функция време-

ни, описывающая искажение закона изменения частоты УМ-ко-