Васюков В.Н. Теория электрической связи

Подождите немного. Документ загружается.

5.7. Импульсная модуляция

193

гауссовскому) закону путем изменения частоты генератора коле-

бания. Демодуляция частотно-манипулированных сигналов может

быть выполнена путем обычного частотного детектирования или

на основе квадратурного приема [11].

5.7. ИМПУЛЬСНАЯ МОДУЛЯЦИЯ

Импульсной модуляцией называется модуляция переносчика,

имеющего вид периодической последовательности импульсов оди-

наковой формы. Модулирующий сигнал при этом является анало-

говым. Фактически при импульсной модуляции параметрами пере-

носчика управляют дискретные отсчеты первичного сигнала,

поэтому, для того чтобы была возможна передача информации без

потерь, частоту следования импульсов переносчика следует выби-

рать исходя из ширины спектра модулирующего сигнала в соот-

ветствии с требованиями теоремы отсчетов.

Как и в случае модуляции гармонического переносчика, виды

модуляции различаются в зависимости от изменяемых параметров.

Если в соответствии с первичным сигналом изменяется амплитуда

импульсов, модуляция называется амплитудно-импульсной

(АИМ), если изменяется длительность (ширина) импульсов – ши-

ротно-импульсной (ШИМ, ДИМ), если изменяется временной

сдвиг (относительно положения импульса в немодулированной

последовательности) – времяимпульсной (ВИМ) или частотно-

импульсной (ЧИМ). Два последних вида модуляции аналогичны

фазовой и частотной модуляции гармонического переносчика в

том смысле, что при изменении временно´го сдвига в соответствии

с первичным сигналом частота следования импульсов меняется

пропорционально его производной.

Рассмотрим более подробно сигнал амплитудно-импульсной

модуляции. Выясним, как связаны спектральные плотности АИМ-

сигнала

()xt

и исходного аналогового сигнала

()xt

. Примем в

качестве переносчика колебание

( ) ( )

s t d t nT









, где

()dt

–

короткий импульс известной формы. Преобразование Фурье для

краткости будем обозначать в операторной форме

F{}

Периодическое колебание

()st

можно записать в виде ряда Фурье

()

jk t

st Сe









5. ПРИНЦИПЫ МОДУЛЯЦИИ И ДЕМОДУЛЯЦИИ

194

где



– коэффициенты ряда, определяемые формой им-

пульса

()dt

. Спектральная плотность переносчика

 

( ) F ( )S s t



очевидно, равна сумме спектральных плотностей гармонических

составляющих (комплексных экспонент) с теми же весовыми ко-

эффициентами, т. е.

( ) F 2 ( )

jk t

S С e С k



 



  







Поскольку АИМ-сигнал получается умножением

( ) ( ) ( )x t x t s t

, его спектральная плотность равна свертке спек-

тральных плотностей сомножителей

( ) ( ) ( )

X X S d





  



( )2 ( )

X C k d







   





()

C X k









и представляет собой совокупность копий спектральной плотности

первичного сигнала

()X 

, сдвинутых по частотной оси на величи-

ны



,k   

и умноженных на весовые коэффициен-

ты, определяемые формой импульса

()dt

. (В частности, при

( ) ( )d t t

все коэффициенты равны 1.)

Очевидно, если каждая копия

()X 

занимает на частотной оси

интервал, ширина которого меньше



, то копии не перекры-

ваются и можно выделить путем фильтрации нижних частот един-

ственную копию

( 0 ) ( )XX  

, тем самым восстановив пер-

вичный сигнал из АИМ-сигнала (т.е. выполнить демодуляцию).

Таким образом, демодуляция АИМ-сигнала выполняется ЛИС-

цепью; это исключение из общего правила

возможно потому, что

Напомним, что в общем случае операции, связанные с модуляцией и

демодуляцией, выполняются с использованием нелинейных или пара-

метрических цепей.

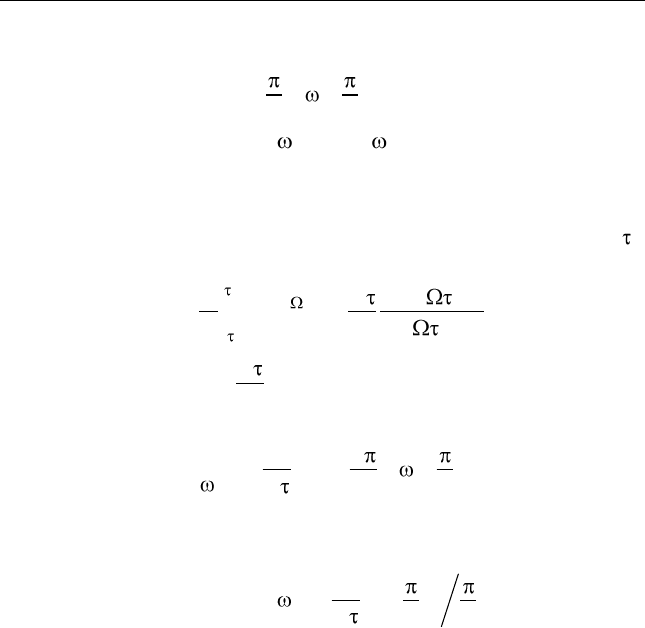
Контрольные вопросы

195

в спектре модулированного сигнала содержатся спектральные

компоненты полезного сигнала и обогащение спектра не требуется.

При этом в интервале

  

спектральная плотность

и0

( ) ( )X СX

Для восстановления первичного сигнала из АИМ-сигнала дол-

жен быть скомпенсирован весовой коэффициент

. Если

()dt

–

прямоугольный импульс с амплитудой

и длительностью ,

симметрично расположенный относительно момента

0t 

, то

- / 2

sin( / 2)

jk t

U U k

C e dt

T T k







Коэффициент



, поэтому восстанавливающий ФНЧ

должен иметь прямоугольную АЧХ вида

, ,

()

0 в противном случае

U T T

















и импульсную характеристику

 

( ) ( ) sinh t F K t t











Заметим, что полученная функция совпадает (с точностью до

амплитудного постоянного множителя) с нулевой базисной функ-

цией ряда Котельникова (все остальные базисные функции обра-

зуются ее сдвигами на величины, кратные шагу дискретизации).

Таким образом, демодуляция АИМ-сигнала по смыслу близка к

восстановлению аналогового сигнала по последовательности его

отсчетов (сравните с разд. 2).

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что такое угол отсечки? Как выбрать оптимальный угол от-

сечки?

2. Для чего используются двухтактные (балансные) схемы?

3. Почему нельзя осуществить модуляцию при помощи ЛИС-цепи?

4. В чем состоит принцип преобразования частоты?

5. ПРИНЦИПЫ МОДУЛЯЦИИ И ДЕМОДУЛЯЦИИ

196

5. Как выбирают параметры нагрузки для диодного детектора?

6. Каким должен быть спектр переносчика, чтобы можно было

осуществить демодуляцию при помощи ЛИС-цепи?

7. При помощи каких схем можно реализовать угловую моду-

ляцию?

8. Как выполнить демодуляцию УМ колебаний?

9. Какие частоты будут присутствовать в спектре тока, проте-

кающего через параметрический элемент, если крутизна меняется

по закону

0 1 1 2 2

( ) cos( ) cos( )s t S S t S t  

, а напряжение – по

закону

0 1 0

( ) cos( )u t U U t

УПРАЖНЕНИЯ

1. Найдите формулы, связывающие коэффициенты в выраже-

ниях (5.2) и (5.9) для

2N 

2. Постройте колебательную характеристику нелинейного уси-

лителя при кусочно-линейной аппроксимации ВАХ нелинейного

элемента (примите

1U 

В,

1,5U 

В,

2S 

мА/В).

3. Повторите расчеты для

1U 

В,

0,5U 

В,

2S 

мА/В.

Сравните результаты.

4. Тональное АМ-колебание характеризуется следующими па-

раметрами. Амплитуда колебания верхней боковой частоты 10 В.

Коэффициент модуляции 0,25. Определите среднюю мощность не-

сущего колебания и отношение суммарной мощности боковых к

мощности несущего. Постройте спектральную диаграмму.

5. Радиопередатчик с амплитудной модуляцией излучает мощ-

ность 10 Вт в отсутствие модулирующего колебания. Найдите пи-

ковую (максимальную) мощность при тональной модуляции, если

коэффициент модуляции равен 0,5; 1.

6. Нелинейный элемент, используемый в амплитудном модуля-

торе, имеет вольт-амперную характеристику

0,01iu

. К диоду

приложено напряжение

( ) 0,5 0,2cos 0,1cosu t t t  

. Опреде-

лите коэффициент модуляции тока (все величины даны в системе

СИ,



– частоты несущего и модулирующего колебаний соот-

ветственно).

7. Запишите выражение для напряжения на параллельном

колебательном контуре диодного модулятора, описанного в

разд. 5.4.2, учитывающее зависимость сопротивление контура от

частоты. Получите выражение, связывающее уменьшение коэффи-

циента модуляции с частотой модулирующего гармонического ко-

лебания и с добротностью контура.

6. ЦЕПИ С ОБРАТНОЙ СВЯЗЬЮ

некоторых случаях полезные изменения

свойств цепей достигаются введением так на-

зываемой обратной связи (ОС). При этом к основной цепи (прямо-

му каналу) подключается цепь обратной связи, через которую вы-

ходной сигнал прямого канала воздействует на его вход (рис. 6.1).

Такая ОС называется внешней. Иногда обратная связь возникает за

счет соответствующего соединения элементов схемы и в ней явно

не выделяется цепь ОС; такая обратная связь называется внутрен-

ней. В некоторых случаях обратная связь возникает против воли

создателя устройства и является нежелательной; такая ОС называ-

ется паразитной.

K(p)

(p)

вх

(p)

вых

(p)

Рис. 6.1. Цепь с обратной связью

При анализе цепей с ОС принято рассматривать входные и вы-

ходные сигналы в операторной форме; соответственно цепи харак-

теризуются операторными передаточными функциями.

Выразим изображение выходного сигнала через передаточную

функцию прямого канала и изображение сигнала на его входе

 

вых вх вых

( ) ( ) ( ) ( ) ( )U p K p U p p U p

Решая это уравнение относительно

вых

()Up

, получаем

вх

вых

( ) ( )

()

1 ( ) ( )

U p K p

p K p





6. ЦЕПИ С ОБРАТНОЙ СВЯЗЬЮ

198

Передаточная функция цепи, охваченной обратной связью,

находится как отношение изображений выходного и входного сиг-

налов

ос

()

1 ( ) ( )

p K p





. (6.1)

От изображений перейдем к частотному описанию цепи; ком-

плексная частотная характеристика цепи с ОС

ос

()

1 ( ) ( )

j K j





. (6.2)

Из полученного выражения видно, что, во-первых, КЧХ цепи с ОС

отличается от КЧХ прямого канала, и, во-вторых, это отличие, оп-

ределяемое знаменателем дроби, различно на разных частотах. Та-

ким образом, обратная связь в общем случае является частотно-

зависимой.

6.1. ВИДЫ ОБРАТНОЙ СВЯЗИ

Влияние ОС на характеристики цепи принципиально различно

в зависимости от того, увеличивается (по модулю) коэффициент

передачи цепи при введении ОС или уменьшается. Различают два

частных случая:

1) если

1 ( ) ( ) 1j K j

, обратная связь называется отри-

цательной;

2) если

1 ( ) ( ) 1j K j

, обратная связь называется поло-

жительной.

Эти два частных случая не исчерпывают всех видов ОС. Очевидно,

возможна ситуация, когда обратная связь является положительной

для одних частотных составляющих и отрицательной для других.

Исторически первой в радиотехнике и связи стали использо-

вать положительную ОС, так как она увеличивает коэффициент

усиления усилителя и используется для самовозбуждения автоге-

нераторов

. Отрицательная ОС была впервые применена

Х. Блэком для расширения полосы пропускания усилителя

Примером более раннего использования отрицательной ОС в технике

вообще можно считать центробежный регулятор Уатта.

Интересные исторические подробности см. в [14].

6.1. Виды обратной связи

199

6.1.1. ПОЛОЖИТЕЛЬНАЯ ОБРАТНАЯ СВЯЗЬ

Рассмотрим резонансный усилитель, в котором обратная

связь создается катушкой обратной связи

св

, индуктивно связан-

ной с колебательным контуром, служащим нагрузкой усилителя

(рис. 6.2). КЧХ усилителя без ОС определяется в окрестности ре-

зонансной частоты

выражением [8]

экв

()







где





– обобщенная расстройка,

– добротность кон-

тура,

экв

– эквивалентное сопротивление контура на резонансной

частоте. Введем обозначение

0 0.7

22Q



для постоянной

времени контура, тогда

экв

0 к

()

1+ ( )







. (6.3)

Введем положительную обратную связь с коэффициентом

(знак ОС определяется полярностью подключения катушки связи,

а абсолютная величина

– соотношением чисел витков катушек),

тогда КЧХ усилителя согласно (6.2) будет равна

 

экв 0 к

экв

ос

экв

0 экв 0 к

0 к

1+ ( )

()

1 ( )

1+ ( )

SR j





  

  



вх

св

вых

Рис. 6.2. Усилитель с ОС

6. ЦЕПИ С ОБРАТНОЙ СВЯЗЬЮ

200

экв

0 экв

1 ( )









Сравнение полученного выражения с (6.3) свидетельствует о

том, что введение ПОС эквивалентно увеличению

экв

0 экв

1 SR

раз, что, в свою очередь, равносильно повышению

добротности контура; степень повышения определяется тем, на-

сколько величина

0 экв

близка к единице. На рис. 6.3 показано

изменение АЧХ резонансного усилителя после введения положи-

тельной ОС. Для этого случая

0 экв

0.75SR 

, поэтому коэффици-

ент усиления на резонансной частоте увеличился в 4 раза, также

в 4 раза уменьшилась полоса пропускания по уровню 0,707. Уси-

литель с ПОС называется регенеративным (иногда положительная

ОС также называется регенеративной).

| K ( j )|

ос

1– SR

экв

Рис. 6.3. Изменение АЧХ усилителя после

введения ПОС

6.1.2. ОТРИЦАТЕЛЬНАЯ ОБРАТНАЯ СВЯЗЬ

Для простоты положим, что цепь обратной связи является

частотно-независимой и коэффициент обратной связи равен

()j 

. Тогда выражение (6.2) принимает вид

()

1 ( )





. (6.4)

6.1. Виды обратной связи

201

Одно из полезных свойств отрицательной ОС состоит в сниже-

нии чувствительности цепи к нестабильности характеристик пря-

мого канала. В большинстве случаев прямой канал содержит ак-

тивные (усилительные) элементы, подверженные старению,

температурному дрейфу и другим вредным факторам. Кроме того,

все активные элементы имеют значительный производственный

разброс параметров, который приводит к изменениям характери-

стик цепи при замене активного элемента (например, при ремонте).

Отрицательная ОС уменьшает чувствительность цепи к подобным

факторам. В самом деле, если в выражении (6.4) положить

( ) 1Kj 

то, очевидно, КЧХ цепи с отрицательной обратной связью (ООС)

()Kj

практически не зависит от прямого канала, а значит, и от его не-

стабильности.

Для более точного анализа рассмотрим полный дифференциал

функции

()Kj

по отношению к коэффициентам передачи пря-

мого и обратного каналов (зависимость от частоты для простоты

выкладок опускается):

OC OC

OC 0

dK dK d



  



   

dK d







откуда получаем

OC 0 0

OC 0 0 0

dK K d

K K K K





Это выражение демонстрирует зависимость относительной неста-

бильности коэффициента усиления цепи с ООС от относительных

6. ЦЕПИ С ОБРАТНОЙ СВЯЗЬЮ

202

нестабильностей прямого и обратного каналов. Видно, что при

1K 

OC 0

dK d



т.е. относительная нестабильность коэффициента усиления цепи с

глубокой ООС определяется только нестабильностью цепи ОС.

Поскольку цепь ОС, как правило, не содержит активных элемен-

тов, ее стабильность на порядки превосходит стабильность прямо-

го канала.

Пример 6.1. Пусть имеется усилитель мощности с коэффици-

ентом усиления 10 и относительной нестабильностью

0,2



Необходимо обеспечить относительную нестабильность в сто раз

меньше [14].

Для этого следует включить каскадно с усилителем мощности

предварительный усилитель с коэффициентом усиления 100 и охва-

тить оба усилителя отрицательной ОС с коэффициентом

0,099

Тогда общий коэффициент усиления останется равным 10:

1000

1 0,099 1000

K 



При этом его относительная нестабильность

OC 0

0,002

K K K





(Здесь принято, что нестабильность цепи ОС пренебрежимо

мала.)◄

Ранее мы увидели, что положительная ОС сужает полосу про-

пускания цепи. Естественно поэтому предположить, что отрица-

тельная ОС должна расширять полосу пропускания, или, что рав-

нозначно, повышать равномерность АЧХ.

Рассмотрим резистивный усилитель, показанный на рис. 6.4.

Комплексная частотная характеристика усилителя определяет-

ся выражением

экв

()





, (6.5)