Васюков В.Н. Теория электрической связи
Подождите немного. Документ загружается.


Упражнение
223
ричного канала без памяти, в котором ошибки при приеме различ-
ных символов являются статистически независимыми. Для такого
канала вероятность получения
r
ошибок при передаче
n
символов
подчиняется биномиальному закону [23]
ош ош
( ) 1
nr
rr
nn
P r C p p
.
Из этого выражения можно найти такие характеристики, как вероят-
ность правильного приема блока из
n
символов
ош
(0) (1 )
n
n
Pp
,
вероятность приема блока, содержащего хотя бы одну ошибку
ош
( 1) 1 (0) 1 (1 )
n
nn
P r P p
, вероятность появления в блоке
m
и более ошибок и т.д.
Память реального дискретного канала проявляется в том, что
вероятность ошибки приема символа зависит от того, какие симво-
лы передавались ранее. Эта зависимость может возникнуть, на-
пример, вследствие межсимвольной интерференции в непрерыв-
ном фильтровом канале. Простейшей моделью дискретного канала
с памятью является марковская модель, согласно которой дискрет-
ный канал может находиться в двух состояниях, каждому из кото-
рых соответствует определенная вероятность ошибки; состояние
канала при приеме очередного символа определяется предыдущим
символом. Более сложной является марковская модель порядка
N
,
в которой состояние канала определяется
N
последними приня-
тыми символами (последовательность состояний канала представ-
ляет собой
N
-связную цепь Маркова
101
).
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что такое канал связи? Как описать канал?
2. Существуют ли линейные стационарные каналы?
3. Что такое многолучевость?
4. Как описываются дискретные каналы?
5. Что такое дискретно-непрерывный канал? Как он описывается?
6. К каким последствиям приводит нелинейность канала?
УПРАЖНЕНИЕ
Выведите формулу определения вероятности появления в бло-
ке из
n
символов
m
и более ошибок для стационарного симмет-
ричного дискретного канала без памяти.
101
Андрей Андреевич Марков (1856 – 1922) – выдающийся русский ма-
тематик, известен своими достижениями в области теории вероятно-
стей и др.

8. ОСНОВЫ ТЕОРИИ ИНФОРМАЦИИ
224
8. ОСНОВЫ ТЕОРИИ
ИНФОРМАЦИИ
8.1. ОСНОВНЫЕ ПОНЯТИЯ И ТЕРМИНЫ
нформация относится к предельно широким
понятиям, которым трудно или невозможно
дать строгое определение, поэтому приходится прибегать к интуи-
ции, объясняя термин «информация» через синонимичные понятия
– «данные», «сведения» и т.п. Однако для решения инженерных
задач требуется количественное определение информации. В тео-
рии и технике связи в настоящее время используется определение
количества информации, предложенное К. Шéнноном
102
.
Для введения этого определения необходимо абстрагироваться
от физического воплощения источника и семантического (смысло-
вого) содержания сообщений. Дискретный источник сообщений то-
гда полностью определяется набором символов (алфавитом)
1
,...,
K
(
K
– объем алфавита) и распределением вероятно-
стей
()P a
, заданным на множестве всех возможных последователь-
ностей символов
1
( ,..., )
n
aaa
,
i
a
произвольной длины. В про-
стейшем случае источника без памяти символы в
последовательности являются независимыми, и распределение
()P a
полностью определяется набором априорных вероятностей отдель-
ных символов
( ), 1,...,
k
p k K
. В более сложных моделях ис-
точников с памятью условная вероятность появления в последова-
тельности определенного символа зависит от того, какие символы
ему предшествуют. Например, в тексте телеграммы на русском язы-
ке после буквы «щ» можно ожидать букв «а», «у», «е», но не «ю»,
102
Клод Элвуд Шеннон (1916 – 2001) – выдающийся американский мате-
матик и инженер, один из основоположников теории информации.
И

8.1. Основные понятия и термины
225
«я», «й» и т.п. Далее, как правило, рассматриваются источники без
памяти.
В процессе передачи информационная последовательность
символов, представляющая собой сообщение, может быть замене-
на другой, кодовой последовательностью, состоящей из символов
кодового алфавита. Целью кодирования может быть более полное
использование канала связи (экономное кодирование) или повы-
шение достоверности передачи (помехоустойчивое кодирование).
Естественно, кодовые последовательности характеризуются дру-
гими распределениями вероятностей, нежели информационные
последовательности.
Канал связи (дискретный) формально описывается входным и
выходным алфавитами
1
,...,
L
xxX
и
1
,...,
M
yyY
разных в
общем случае объемов
L
и
M
и условным распределением веро-
ятностей
( | )P yx
, заданным для всех возможных последовательно-
стей
y
и
x
произвольной длины. Условное распределение
( | )P yx
описывает вероятностный механизм действия помех в канале.
В простейшем случае канала без памяти распределение
( | )P yx
полностью определяется набором условных вероятностей для всех
пар отдельных символов
( | )
ji
P y x
,
i
x X
,
j
y Y
.
Информация, согласно современным представлениям, – это
свойство сообщения снимать (или уменьшать) неопределенность
относительно исхода некоторого случайного опыта (например, от-
носительно переданного символа). Действительно, во всех реаль-
ных случаях получатель сообщения что-то знает о некотором объ-
екте или событии до опыта («a priori»), но ему известно не все,
иначе не было бы необходимости передавать сообщение. Напри-
мер, футбольный болельщик знает, с кем сегодня играла его люби-
мая команда, но не знает, кто победил. Таким образом, до опыта
(до получения сообщения) налицо некоторая неопределенность.
После приема сообщения неопределенность исчезает (или, по
крайней мере, уменьшается) вследствие получения информации.
Количество получаемой информации, очевидно, должно быть свя-
зано со степенью снимаемой неопределенности. Так, принимая со-
общение о событии, которое достоверно известно, информации мы
не получаем.
Количественная мера информации должна удовлетворять сле-
дующим интуитивно очевидным требованиям:
если исход опыта единствен (достоверное событие), то коли-
чество информации в сообщении о нем должно быть равно нулю;

8. ОСНОВЫ ТЕОРИИ ИНФОРМАЦИИ
226
количество получаемой информации тем больше, чем более
неожиданным является исход;
общее количество информации в нескольких сообщениях об
исходах опытов, независимых в вероятностном смысле, должно
равняться сумме количеств информации в отдельных сообщениях
(аддитивность информации).
Мера неожиданности сообщения
a
в виде
1/ ( )P a
удовлетворя-
ет второму требованию, однако она не равна нулю для достоверно-
го события и не обладает свойством аддитивности: неожиданность
двух независимых сообщений
1
a
и
2
a
равна, очевидно,
12
1/[ ( ) ( )]PPaa
. Чтобы обеспечить выполнение всех требований,
необходимо определить частное (индивидуальное) количество ин-
формации в сообщении выражением
1
log log ( )
()
mm
P
P
a
a
.
Основание логарифма может быть произвольным и определяет
лишь масштаб (единицу измерения). Общепринятым является ос-
нование 2, при этом единица называется битом
103
. Учитывая это, в
дальнейшем всюду будем использовать двоичный логарифм без
явного указния его основания.
Поскольку событие, состоящее в выдаче сообщения
a
, случай-
но и происходит с вероятностью
()P a
, количество информации,
связанное с этим сообщением, также является случайной величи-
ной. Введем величину
( ) log ( )
ii
Ip
,
называемую собственной информацией символа
i
.
Информационная производительность дискретного источника
характеризуется средним количеством информации на символ, ко-
торое определяется как математическое ожидание этой случайной
величины. Рассматривая для простоты источник без памяти, запи-
шем среднее количество информации, приходящееся на один сим-
вол и называемое энтропией дискретного источника , в виде
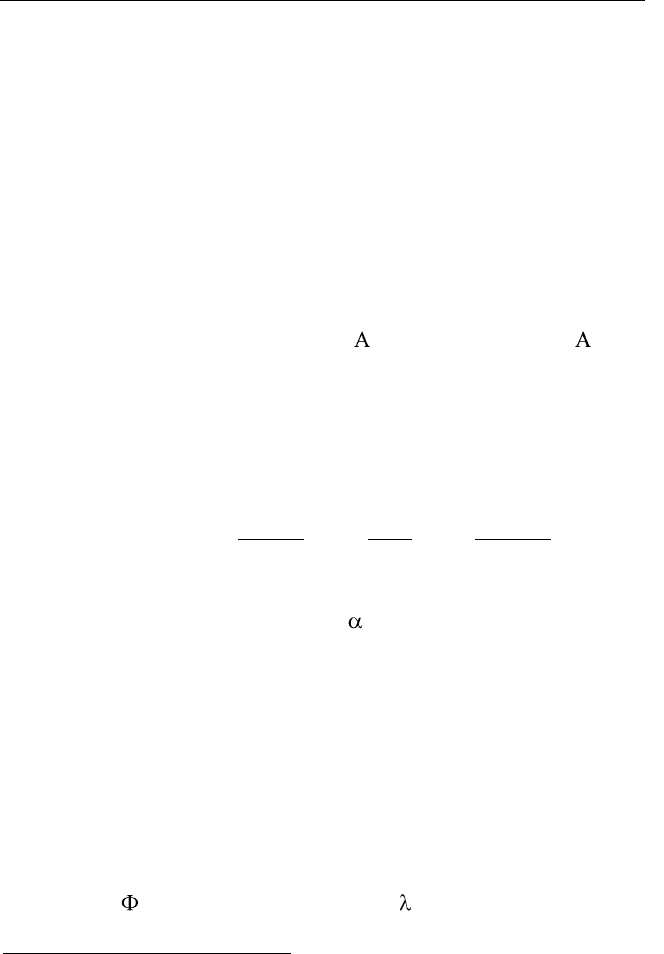
1
( ) ( )log ( )
K
kk
k
H p p
. (8.1)
103
В литературе упоминаются единицы нат и хартли, соответствующие
основаниям логарифма е и 10.
8.2. Энтропия и информация
227
Пример 8.1. Предположим, что передается сообщение о карте,
вытащенной наугад из идеально перетасованной колоды в 32 карты
(вероятность вытащить любую карту равна при этих условиях
1/32). Очевидно, это сообщение несет количество информации,
равное 5 битам. Если это сообщение разбить на два так, что внача-
ле сообщается масть карты, а затем ее достоинство, то это количе-
ство информации будет передано частями – сначала 2 бита, затем
еще 3. (Убедитесь, что это действительно так!) ◄
8.2. ЭНТРОПИЯ И ИНФОРМАЦИЯ
Рассмотрим основные свойства энтропии.
1. Энтропия любого источника неотрицательна
( ) 0H
.
Это следует из того, что вероятность любого события неотрица-
тельна и не превосходит единицы. Энтропия источника равна нулю
в том случае, если один из символов имеет вероятность 1, а ос-
тальные – 0. Неопределенность, возникающая вследствие того, что
log p
при
0p
, может быть раскрыта с применением пра-
вила Лопиталя:
00
log1/ log 1/ log
lim( log ) lim lim lim 0
1/ 1
p p q q
p q q e
pp
pq
.
2. При заданном объеме алфавита
K
энтропия максимальна,
если все символы равновероятны
( ) 1/
kk
p p K
.
Доказательство состоит в нахождении условия максимума эн-
тропии при ограничении
1
1
K
k
k
p
. Задачу поиска экстремума
функции при наличии ограничения можно свести к обычному на-
хождению экстремума (без ограничения) другой функции, состоя-
щей из двух слагаемых
104
. Первое слагаемое представляет собой в
нашем случае энтропию, которую необходимо максимизировать, а
второе слагаемое равно нулю, когда выполняется ограничивающее
условие. Составим целевую функцию в виде
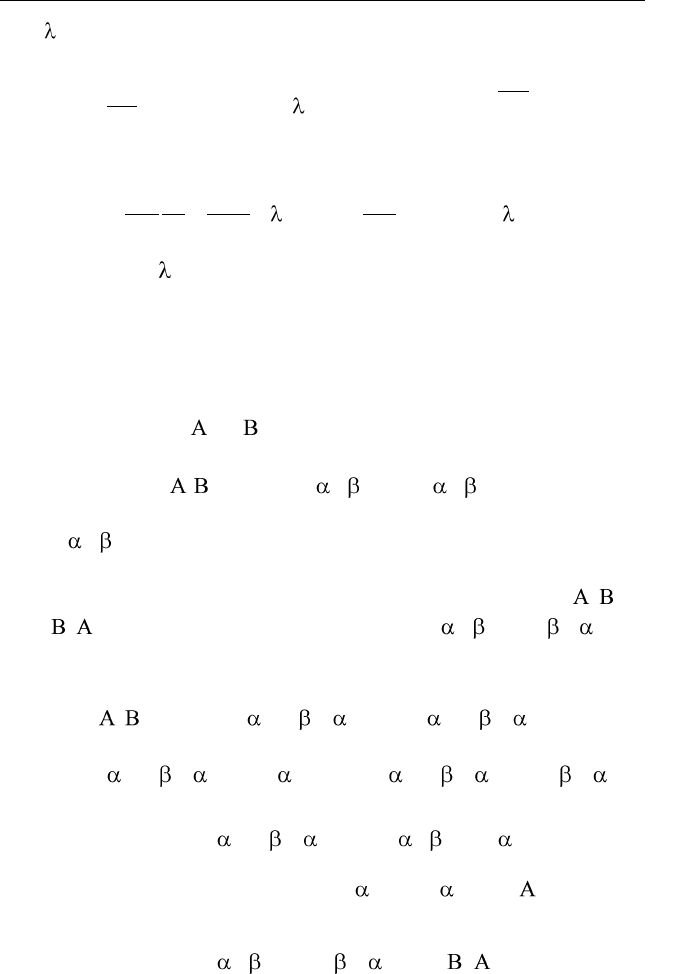
1
11
( ,..., ) log 1
KK
K k k k
kk
p p p p p
,
104
Этот метод называется методом неопределенных множителей Лаг-
ранжа.
8. ОСНОВЫ ТЕОРИИ ИНФОРМАЦИИ
228
где – неопределенный множитель Лагранжа, и запишем усло-
вие достижения ее экстремума
11
log 1 0
KK
k k k
kk
i
p p p
p
,
1,iK
.
Решая уравнения относительно
i
p
, получаем
ln
1 1 1
0 1 ln 0
ln2 ln2 ln 2
i
ii
i
p
pp
p
,
откуда
exp( ln2 1)
i
p
независимо от
i
, а это и означает равно-
вероятность символов. Максимальное значение энтропии равно
max
logHK
. В частности, при
2K
энтропия максимальна при
12
1/2pp
и равна 1 биту. Таким образом, 1 бит – это количе-
ство информации, доставляемое одним из двух равновероятных
символов, вырабатываемых источником без памяти.
Два источника и , рассматриваемых в совокупности, ха-
рактеризуются совместной энтропией
( , ) ( , )log ( , )
i j i j
ij
H p p
,
где
( , )
ij
p
– совместная вероятность символов; суммирование
проводится по всем возможным значениям индексов. Совместная
энтропия характеризуется свойством коммутативности
( , )H
( , )H
, что прямо следует из равенства
( , ) ( , )
i j j i
pp
.
Используя выражение для совместной вероятности, перепишем
совместную энтропию в виде
( , ) ( ) ( | )log ( ) ( | )
i j i i j i
ij
H p p p p
( ) ( | )log ( ) ( ) ( | )log ( | )
i j i i i j i j i
i j i j
p p p p p p
.
Заметим, что
( ) ( | ) ( , ) ( )
i j i i j i
jj
p p p p
, тогда пер-
вое слагаемое принимает вид
( )log ( ) ( )
ii
i
p p H
, а второе
слагаемое представляет собой условную энтропию
( , )log ( | ) ( | )
i j j i
ij
p p H
.

8.2. Энтропия и информация
229
Таким образом, совместная энтропия
( , ) ( ) ( | ) ( ) ( | )H H H H H
. (8.2)
Если источники статистически независимы, то
( , ) ( ) ( )H H H
,
что согласуется с интуитивным представлением об аддитивности
информации от независимых источников.
Рассмотрим более подробно понятие условной энтропии.
Предположим, что имеется дискретный канал связи, на входе ко-
торого задан алфавит , а на выходе алфавит ; канал описыва-
ется условным распределением
( | )P
. Можно считать, что на
входе действует источник с алфавитом и энтропией
()H
, а на
выходе – источник с алфавитом и энтропией
()H
, причем эти
источники статистически связаны.
Условное распределение
( | )P
описывает вероятностную
связь входных и выходных символов. Чем сильнее эта связь, тем
более уверенно можно судить о входных символах на основании
наблюдения выходных, тем лучше канал передает информацию.
Количество информации в символе
j
относительно символа
i
определяется выражением
( | )
( ; ) log
()
ij
ij
i
p
I
p
. (8.3)
В самом деле, если символы независимы, то
( | ) ( )
i j i
pp
и
( ; ) 0
ij
I
(символ
j
не несет информации о символе
i
).
И, наоборот, при жесткой (детерминированной) связи между сим-
волами
i
и
j
, очевидно,
( | ) 1
ij
p
, поэтому
1
( ; ) log ( )
()
i j i
i
II
p
, т. е. количество информации в симво-
ле
j
относительно символа
i
равно собственному количеству
информации в символе
i
(или, что эквивалентно, в символе
j
).
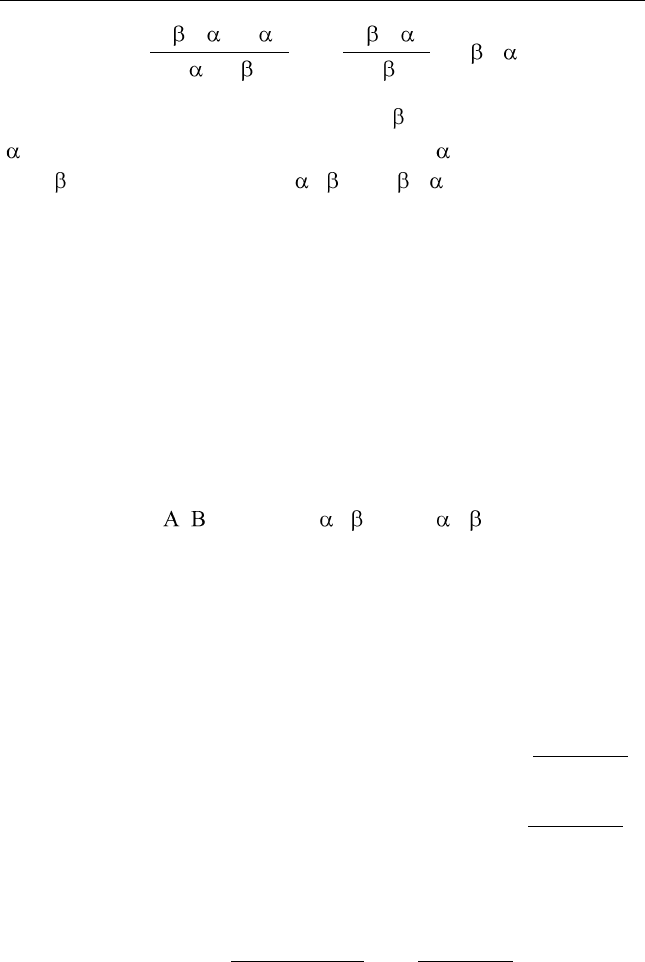
Используя известные формулы для совместных и условных ве-
роятностей, легко видеть, что
( | ) ( ) ( , )
( ; ) log log
( ) ( ) ( ) ( )
i j j i j
ij
i j i j
p p p
I
p p p p
8. ОСНОВЫ ТЕОРИИ ИНФОРМАЦИИ
230
( | ) ( ) ( | )
log log ( ; )
( ) ( ) ( )
j i i j i
ji
i j j
p p p
I
p p p
.
Количество информации в символе
j
относительно символа
i
равно количеству информации в символе
i
относительно сим-
вола
j
. Поэтому величина
( ; ) ( ; )
i j j i
II
называется взаим-
ной информацией указанных символов.
Очевидно, в силу вероятностной связи входных и выходных
символов наблюдение выходной последовательности символов не
снимает полностью неопределенности относительно переданного
сообщения. Иными словами, представляет интерес вопрос: какова
энтропия входного алфавита при условии наблюдения выходных
символов? Очевидно, что чем меньше эта условная энтропия, тем
лучше канал передает информацию. Частное количество информа-
ции во входном символе определяется, как и раньше, но с заменой
безусловных вероятностей условными, усреднение же производит-
ся по всем возможным сочетаниям входного и выходного символов
(по совместному распределению вероятностей):
11
( ) ( , )log ( | )
LM
i j i j
ij
H p p|
. (8.4)
Пример 8.2. Предположим, что на входе двоичного канала
действует источник с равновероятными символами 0 и 1, а иска-
жения символов при передаче происходят с некоторыми вероятно-
стями
0
( 1| 0)p p y x
и
1
( 0| 1)p p y x
.
Найдем количество информации в выходном символе относи-
тельно входного. Безусловные вероятности выходных символов
01
1
( 0) ( 0| 0) ( 0) ( 0| 1) ( 1)
2
pp
p y p y x p x p y x p x
;
10
1
( 1) ( 1| 0) ( 0) ( 1| 1) ( 1)
2
pp
p y p y x p x p y x p x
.
Взаимная информация переданного символа
0x
и наблю-
даемого символа
0y
равна
0
01
2(1 )
( 0 | 0)
(0;0) log log
( 0) 1
p
p y x
I
p y p p
,

8.2. Энтропия и информация
231
аналогично взаимная информация переданного символа
1x
и
наблюдаемого символа
0y
равна
1
01
2
( 0 | 1)
(1; 0) log log
( 0) 1
p
p y x
I
p y p p
.
Так же находятся два оставшихся количества информации:
0
10
2
( 1| 0)
(0;1) log log
( 1) 1
p
p y x
I
p y p p
,
1
10
2(1 )
( 1| 1)
(1;1) log log
( 1) 1
p
p y x
I
p y p p
.
Особый интерес представляют некоторые частные случаи.
Первый случай соответствует каналу без помех и характеризу-
ется вероятностями
01
0pp
. Тогда, очевидно,
(0; 0) (1;1) 1II
. Поскольку энтропия источника равна 1 биту и
взаимная информация входных и выходных символов равна также
1 биту при их совпадении, такой канал обеспечивает передачу ин-
формации без потерь.
Второй частный случай имеет место при
01
0.5pp
. Тогда
(0; 0) (1;1) (0;1) (1; 0) 0I I I I
и канал не передает информации
(такая ситуация называется «обрывом канала»). ◄
Рассмотрим основные свойства условной энтропии.
1. Если источники сообщений и являются независимыми,
то условная энтропия равна безусловной:
( | ) ( )HH
,
( | ) ( )HH
.
Действительно, если источники независимы, то
( | ) ( )
i j i
pp
при всех
,ij
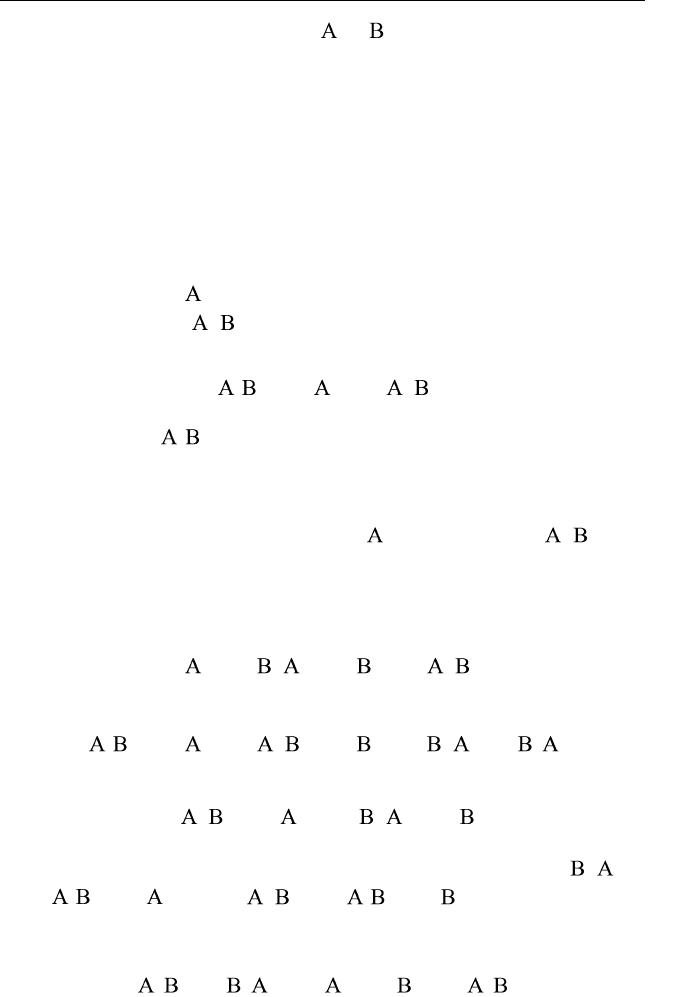
. Тогда выражение (8.4) можно пе-
реписать в виде
1 1 1 1
( ) ( , )log ( ) log ( ) ( , )
L M L M
i j i i i j
i j i j
H p p p p|
.
Но
1
( , ) ( )
M
i j i
j
pp
, откуда немедленно следует
1
( ) ( )log ( ) ( )
L
ii
i
H p p H|
, что и требовалось доказать.
8. ОСНОВЫ ТЕОРИИ ИНФОРМАЦИИ
232
2. Если символы источников и жестко связаны, то услов-
ная энтропия равна нулю. В самом деле, при жесткой связи в вы-
ражении (8.4) некоторые условные вероятности равны 1, а осталь-
ные 0. Но как было показано выше, в этом случае сумма равна
нулю.
Для условий примера 8.2 жесткая (детерминированная) связь
входных и выходных символов соответствует вероятностям оши-
бок
01
0pp
(или
01
1pp
).
3. Условная энтропия входного алфавита относительно выход-
ного характеризует передаваемую по каналу информацию сле-
дующим образом. Если энтропия входного источника в отсутствие
передачи равна
()H
, а после приема выходного символа она ста-
новится равной
( | )H
, то, очевидно, среднее количество пере-
даваемой информации на символ равно разности
( , ) ( ) ( | )I H H
.
Величина
( , )I
представляет собой взаимную информацию
входа и выхода.
Если потери информации отсутствуют (канал без помех), то ус-
ловная энтропия источника после передачи равна 0, количество
передаваемой информации равно
()H
. Величина
( | )H
, та-
ким образом, характеризует потери информации в канале и назы-
вается ненадежностью [10].
Заметим, что из выражения (8.2) для совместной энтропии сле-
дует
( ) ( | ) ( ) ( | )H H H H
,
поэтому
( , ) ( ) ( | ) ( ) ( | ) ( , )I H H H H I
. (8.5)
При очень высоком уровне помех условные энтропии равны
безусловным (
( | ) ( )HH
,
( | ) ( )HH
) и количество
информации, передаваемой по каналу, становится равным нулю.
4. Из выражения для совместной энтропии
( | )H
( , ) ( )HH
и
( | ) ( , ) ( )H H H
. Подставляя эти
выражения в (8.5), получаем среднее количество передаваемой ин-
формации на символ
( , ) ( , ) ( ) ( ) ( , )I I H H H
. (8.6)
