Васюков В.Н. Теория электрической связи

Подождите немного. Документ загружается.

8.3. Пропускная способность дискретного канала

233

Приведем выражение (8.6) к более удобному виду, для чего

подставим в него формулы для вычисления безусловной и совме-

стной энтропии.

1 1 1 1

( ) ( , )log ( ) ( , )log ( )

L M L M

i j i i j j

i j i j

I p p p p

   

    

   

1 1 1 1

( , )

( , )log ( , ) ( , )log

( ) ( )

L M L M

i j i j i j

i j i j

p p p

   



   

. (8.7)

8.3. ПРОПУСКНАЯ СПОСОБНОСТЬ

ДИСКРЕТНОГО КАНАЛА

Если источник вырабатывает символы со скоростью

пп

1/vT

где

– время передачи одного символа, то производительность

источника определяется как

пп

'/H Hv H T

и имеет размерность

бит/с. Поскольку количество информации на один символ состав-

ляет при передаче по каналу величину

()I 

, определяемую вы-

ражением (8.7), скорость передачи информации по каналу

()

'( )





бит/с.

Рассмотрим выражение (8.5), которое характеризует количест-

во информации на символ, передаваемое по дискретному каналу

связи, на входе которого действует источник с алфавитом , а на

выходе образуются символы из алфавита . Заметим, что энтро-

пия

()H

определяется только источником входных символов, в

то время как

()H

()H 

зависят также от свойств

канала. Таким образом, скорость передачи информации по каналу

зависит и от свойств источника, и от свойств канала. Для того что-

бы охарактеризовать только канал, находят максимум скорости

передачи информации по данному каналу при всевозможных ис-

точниках (имеется в виду, что при одном и том же алфавите пере-

бираются всевозможные распределения вероятностей его симво-

лов). Максимальная скорость передачи информации, которая

может быть достигнута для данного канала, называется его пропу-

скной способностью

( ) ( )

max '( ) max ( )

P A P A

C I I

   

бит/с.

8. ОСНОВЫ ТЕОРИИ ИНФОРМАЦИИ

234

Заметим, что нахождение пропускной способности реального

канала связи представляет собой сложную задачу. В простейшем

случае бинарного канала без помех (см. пример 8.2) пропускная

способность численно равна скорости модуляции

пп

1/vT

Очевидно, скорость передачи информации по определению не

может быть больше пропускной способности канала. Можно рас-

сматривать также пропускную способность канала на символ [10]

симв

()

max ( )

CI

Пример 8.3. Найдем пропускную способность стационарного

симметричного канала без памяти. Как было указано в разд. 7, для

такого канала входной и выходной алфавиты совпадают

, 1,

kK

, а вероятность ошибки одинакова для всех симво-

лов и при этом выполняется условие

 

ош

( 1), если ,

1 , если ,

p K l k

p l k













Найдем согласно (8.4) условную энтропию

( ) ( , )log ( | )

i j j i

H p p|



  



( ) ( | )log ( | )

i j i j i

p p p



  



ош ош

( ) log (1 )log(1 )

p p p







     











ош

ош ош ош

(1 )log(1 ) log

p p p

    



. (8.8)

В последнем преобразовании учтено, что выражение в квадрат-

ных скобках не зависит от

, поэтому сумма вероятностей

()

равная 1, как сомножитель исчезает, а суммирование в квадратных

скобках по

ji

эквивалентно умножению на

( 1)K 

. Очевидно,

выражение (8.8) не зависит от распределения вероятностей переда-

ваемых символов, поэтому выражение (8.5)

( , ) ( ) ( | )I H H

8.4. Кодирование источника

235

достигает максимума, когда максимальна энтропия

()H

, что оз-

начает равновероятность символов выходного алфавита, а это, в

свою очередь, имеет место, когда равновероятны символы входно-

го алфавита (что очевидно в силу симметрии канала). Таким обра-

зом, пропускная способность стационарного симметричного кана-

ла без памяти (на символ) равна

ош

симв ош ош ош

log (1 )log(1 ) log

C K p p p

    



. ◄

8.4. КОДИРОВАНИЕ ИСТОЧНИКА

Реальные источники редко обладают максимальной энтропи-

ей, поэтому их принято характеризовать так называемой избыточ-

ностью, определяемой выражением

max





Для независимых источников (источников без памяти) избы-

точность равна нулю (а энтропия максимальна) при равновероят-

ности символов. Для источников с памятью избыточность тем

больше, чем выше степень статистической зависимости символов в

сообщении, при этом неопределенность относительно очередного

символа в сообщении уменьшается, соответственно уменьшается и

количество информации, переносимое этим символом. Например,

в естественном английском языке после буквы q всегда следует

буква u, поэтому при передаче такого текста буква u, следующая за

буквой q, информации не несет. (В реальном английском тексте

могут встречаться аббревиатуры, например, «QWERTY», а также

иноязычные, например французские слова, для которых указанная

закономерность не выполняется.)

Объем алфавита источника и количество различных символов,

передаваемых по каналу (канальных символов), могут не совпа-

дать. В таких случаях один символ источника представляется (ко-

дируется) последовательностью из нескольких кодовых символов

(кодовым словом, или кодовой комбинацией). Если для всех сим-

волов источника длина кодовых слов одинакова, код называют

равномерным, в противном случае – неравномерным. Примером

равномерного кода является код Бодó, смысл которого состоит в

представлении каждой из букв алфавита двоичным числом фикси-

рованной разрядности (например, для алфавита из 32 символов,

8. ОСНОВЫ ТЕОРИИ ИНФОРМАЦИИ

236

включающего 26 латинских букв и знаки препинания, достаточно

пятиразрядного кода Бодо). При передаче сообщений неравномер-

ным кодом говорят о средней длине кодового слова (усреднение

длин кодовых слов производится по соответствующему распреде-

лению вероятностей).

Шеннону принадлежит следующая теорема (доказательство

см., например, в [10]), называемая основной теоремой о кодирова-

нии в отсутствие шумов.

ТЕОРЕМА. Среднюю длину кодовых слов для передачи симво-

лов источника при помощи кода с основанием

можно как

угодно приблизить к величине

( )/ logHm

Смысл теоремы состоит в том, что она определяет нижнюю

границу длины кодовых слов и устанавливает принципиальную

возможность достичь этой границы, однако она не указывает спо-

собов достижения.

Пример 8.4. Если источник имеет объем алфавита 32, то при

равновероятных символах его энтропия равна 5 битам. Тогда для

двоичного кода наименьшая средняя длина составляет 5, следова-

тельно, пятизначный код Бодо является оптимальным кодом. Од-

нако при неравных вероятностях символов энтропия источника

меньше чем 5 бит (избыточность источника отлична от нуля), сле-

довательно, можно найти код со средней длиной кодового слова

меньше пяти и таким образом повысить скорость передачи ин-

формации. Текст на русском языке, например, имеет энтропию

около 2,5 бит, поэтому путем соответствующего кодирования

можно увеличить скорость передачи информации вдвое против

пятиразрядного равномерного кода Бодо (чтобы использовать код

Бодо для передачи русского текста, можно отождествить буквы «е»

и «ѐ», а также «ь» и «ъ»). ◄

Практическое значение теоремы Шеннона заключается в воз-

можности повышать эффективность систем передачи информации

(систем связи) путем применения экономного кодирования (коди-

рования источника).

Очевидно, что экономный код должен быть в общем случае не-

равномерным. Общее правило кодирования источника (без памяти)

состоит в том, что более вероятным символам источника ставят-

ся в соответствие менее длинные кодовые слова (последователь-

ности канальных символов).

Пример 8.5. Известный код Морзе служит примером неравно-

мерного кода. Кодовые слова состоят из трех различных символов:

точки (передается короткой посылкой), тире ― (передается отно-

сительно длинной посылкой) и пробела (паузы). Наиболее частой

8.4. Кодирование источника

237

букве в русском тексте – букве «е» – соответствует самое короткое

кодовое слово, состоящее из одной точки, относительно редкая

буква «ш» передается кодовым словом из четырех тире, разделен-

ных пробелами, и т.д. ◄

Кодирование источника по методу Шеннона – Фано

Принцип построения кода Шеннона – Фано состоит в упорядо-

чении всех символов алфавита (назовем их для краткости «буква-

ми») по убыванию вероятностей. Затем все буквы делятся на две

(неравные в общем случае) группы так, что сумма вероятностей

букв для обеих групп одинакова или примерно одинакова, и в ка-

честве первого символа кодового слова каждой букве первой груп-

пы присваивается кодовый символ 0, а каждой букве второй груп-

пы – символ 1 (или наоборот). Далее первая и вторая группы

делятся на подгруппы в соответствии с принципом равной вероят-

ности, и эта процедура продолжается до тех пор, пока алфавит ис-

точника не будет исчерпан. Пример построения кода Шеннона –

Фано приведен в табл. 8.1.

Т а б л и ц а 8.1

Построение кода Шеннона – Фано

Символ и его

вероятность

Комбинация кодовых символов

Длина

комбинации

()

1-й

2-й

3-й

4-й

5-й

6-й

1/4

1/8

1/16

1/32

1/64

На первом шаге процедуры все символы алфавита источника

делятся на две группы, причем в первую группу входят символы

, которым соответствует суммарная вероятность 1/2, а во

вторую – все остальные символы. Символам

приписыва-

ется в качестве первого кодового символа символ 0, а всем осталь-

8. ОСНОВЫ ТЕОРИИ ИНФОРМАЦИИ

238

ным символам источника – кодовый символ 1. На втором шаге

первая и вторая группы рассматриваются по отдельности, при этом

в первой группе содержатся всего два символа, которые получают

в качестве второго кодового символа 0 и 1 соответственно. Таким

образом, символу источника

ставится в соответствие кодовое

слово 00, а символу

– слово 01. Вторая группа символов источ-

ника, включающая символы

, делится на две час-

ти в соответствии с их вероятностями, при этом символ

, кото-

рому соответствует вероятность 1/4, получает в качестве второго

символа кодового слова символ 0, а остальные символы источни-

ка – символ 1. Далее процесс продолжается до тех пор, пока не ос-

танется группа из двух символов – в данном примере это симво-

лы

, – которым присваиваются кодовые символы 0 и 1.

Необходимо обратить внимание на следующее свойство полу-

ченного кода: ни одна кодовая комбинация не является началом ка-

кой-либо другой кодовой комбинации (так называемое префиксное

правило). Такие коды называются неперекрываемыми (неприводи-

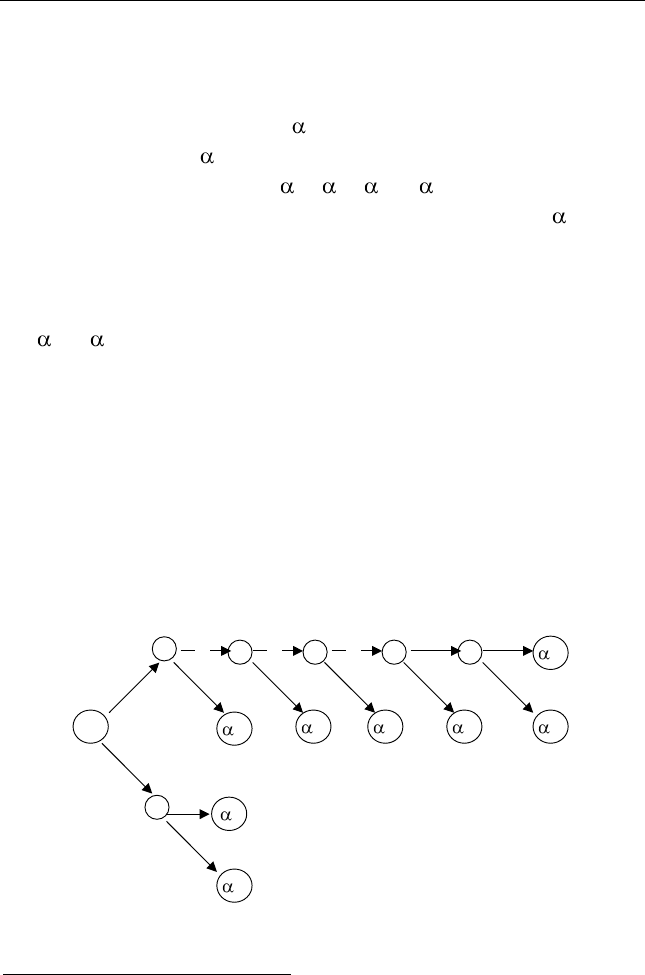
мыми). Декодирование неприводимого кода может быть осуществ-

лено на основе дерева декодирования

105

(рис. 8.1), отвечающего

некоторому конечному автомату, который переходит из начально-

го состояния в другие состояния в соответствии с очередным сим-

волом кодовой последовательности.

Перед декодированием конечный автомат устанавливается в

начальное состояние НС, а дальнейшие переходы зависят только

НС

Рис. 8.1. Дерево декодирования для кода Шеннона– Фано

(табл. 8.1)

105

Деревом называется граф, не содержащий циклов (замкнутых путей).

8.4. Кодирование источника

239

от поступающих символов кода, при этом все концевые состояния

(«листья» дерева) соответствуют декодированным символам алфа-

вита источника; по достижении листа автомат переходит вновь в

начальное состояние. Поскольку с поступлением последнего кодо-

вого символа декодирование кодового слова всегда заканчивается,

префиксные коды называют также мгновенными [16]. Существуют

однозначно декодируемые коды, не обладающие префиксным

свойством и не являющиеся мгновенными, однако их декодирова-

ние требует больших объемов памяти декодера и приводит к

большим задержкам результата.

Средняя длина кодовой комбинации для построенного кода

()







0,75 2 0,125 3 0,0625 4 0,03125 5 0,03125 6 2,469          

Согласно теореме Шеннона при оптимальном кодировании

можно достичь средней длины

min

( ) / log2 ( )log ( ) 2.469

H p p



   



Таким образом, построенный код является оптимальным. Так

получилось вследствие того, что на каждом шаге процедуры по-

строения кода удавалось разделить символы на группы с равными

вероятностями. Заметим, что восемь различных символов источни-

ка можно представить восемью комбинациями равномерного дво-

ичного кода (Бодо), при этом длина каждой кодовой комбинации

равняется, очевидно, трем. Уменьшение средней длины кодовой

комбинации (и, следовательно, увеличение скорости передачи ин-

формации) составляет в данном примере около 22 %. Если при де-

лении символов на группы их суммарные вероятности оказывают-

ся неравными, выигрыш может быть не столь значительным.

Определим вероятность появления определенного символа в

кодовой комбинации (пусть это будет символ 1). Очевидно, ее

можно найти следующим образом: а) подсчитать количества еди-

ниц во всех кодовых словах; б) умножить эти количества на веро-

ятности соответствующих кодовых слов; в) просуммировать полу-

ченные величины; г) отнести результат к средней длине кодового

слова. Таким образом,

0,25 0,25 2 0,125 3 0,0625 4 0,03125 (5 6) 0,015625

2,469

(1) 0,5p

         



8. ОСНОВЫ ТЕОРИИ ИНФОРМАЦИИ

240

Итак, при оптимальном кодировании источника кодовые сим-

волы равновероятны; такое кодирование является безызбыточным.

Источник вместе с кодером можно рассматривать как новый ис-

точник с алфавитом, состоящим из кодовых символов; энтропия и

избыточность этого источника – это энтропия и избыточность ко-

да. Оптимальный код имеет максимальную энтропию и нулевую

избыточность.

Кодирование источника по методу Хаффмена.

Другим широко известным методом кодирования источника

является метод Хаффмена

106

. Процедура кодирования состоит из

следующих шагов.

1. Все символы алфавита записываются в порядке убывания

вероятностей.

2. Два нижних символа соединяются скобкой, из них верхнему

приписывается символ 0, нижнему 1 (или наоборот).

3. Вычисляется сумма вероятностей, соответствующих этим

символам алфавита.

4. Все символы алфавита снова записываются в порядке убы-

вания вероятностей, при этом только что рассмотренные символы

«склеиваются», т.е. учитываются как единый символ с суммарной

вероятностью.

5. Повторяются шаги 2, 3 и 4 до тех пор, пока не останется ни

одного символа алфавита, не охваченного скобкой.

Скобки в совокупности образуют дерево. Код Хаффмена для

некоторого символа алфавита находится путем последовательной

записи нулей и единиц, встречающихся на пути от корня дерева

(корню соответствует суммарная вероятность 1) до листа, соответ-

ствующего данному символу. Полученное дерево, очевидно, явля-

ется деревом декодирования.

Для примера, показанного на рис. 8.2, получаются следующие

кодовые комбинации:

11;

01;

101:

100;

001;

0000;

00011;

00010.

Энтропия алфавита

( ) 2,628H 

. Средняя длина кодового

слова







0,3 2 + 0,2 2 + 0,15 3 + 0,15 3 + 0,1 3 +

+ 0,04 4 + 0,03 5 + 0,03 5 = 2,66.

106

Доказана оптимальность кода Хаффмена в смысле наименьшей сред-

ней длины кодовых слов [16].

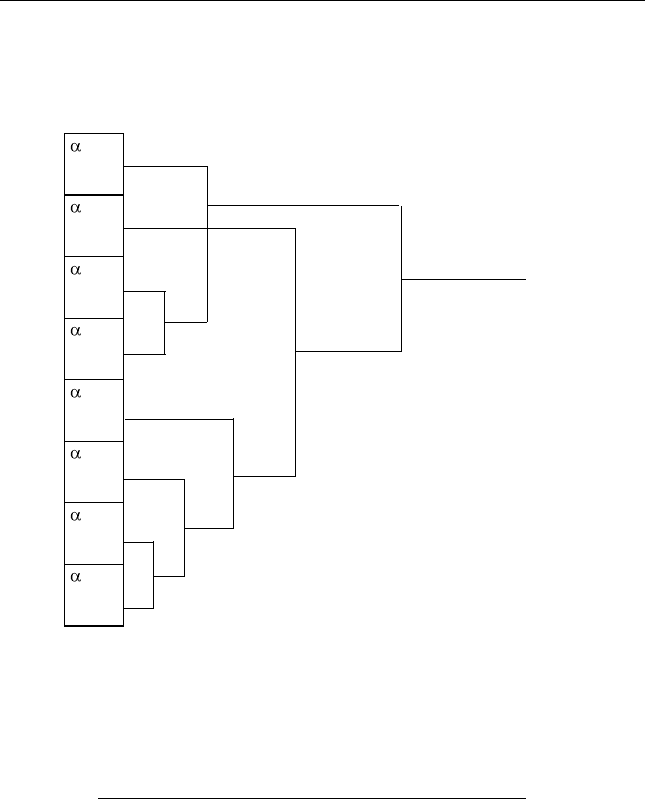
8.4. Кодирование источника

241

Следовательно, код не оптимален, но очевидно, что он доволь-

но близок к оптимальному. Для сравнения: равномерный код для

этого случая имеет среднюю длину кодового слова 3 (совпадаю-

щую для равномерного кода с длиной каждого кодового слова).

0,3

0,2

0,15

0,1

0,04

0,03

НС

Рис. 8.2. Дерево декодирования для кода Хаффмена

Вероятность символа 1 в последовательности кодовых комби-

наций находится как среднее количество единиц, отнесенное к

средней длине кодового слова

2 0,3 0,2 2 0,15 0,15 0,1 2 0,03 0,03

(1) 0,541

2,66

        



Неоптимальность кода проявляется в неравенстве вероятностей

кодовых символов (0,541 для 1 и 0,459 для 0). Избыточность кода,

как легко видеть, равна 0.005.

8. ОСНОВЫ ТЕОРИИ ИНФОРМАЦИИ

242

ЗАМЕЧАНИЯ

1. Из рассмотренных примеров не должно составиться лож-

ное впечатление, будто код Шеннона – Фано оптимален, а код

Хаффмена – нет. Оптимальность кода Шеннона – Фано в рас-

смотренном примере объясняется специально подобранными ве-

роятностями символов, так, что на каждом шаге вероятности

делятся ровно пополам.

2. В приведенных примерах предполагалось, что символы в со-

общении являются независимыми (т. е. вероятность появления в

сообщении любых двух символов рядом равна произведению веро-

ятностей появления каждого из символов в отдельности). В ре-

альных сообщениях на естественных языках символы не являются

независимыми; в таких случаях следует кодировать не отдельные

символы (буквы), а группы букв или слова. Это уменьшает зависи-

мость и повышает эффективность кода.

3. Кодирование групп символов вместо отдельных символов

также повышает эффективность кодирования в случае незави-

симого источника с сильно различающимися вероятностями сим-

волов, как это видно из следующего примера.

Пример 8.6. Рассмотрим источник, вырабатывающий два неза-

висимых символа с вероятностями 0,1 и 0,9. В этом тривиальном

случае методы кодирования Хаффмена и Шеннона – Фано приво-

дят к одинаковому коду: символы алфавита кодируются символами

0 и 1. Пусть для определенности

0

;

1

. Энтропия ис-

точника равна

()H

=0,469; средняя длина кодового слова равна 1,

избыточность источника и избыточность кода одинаковы и равны

max

( ) ( )

1 0,469

0,531

( ) 1



  

Применим кодирование группами по 2 символа алфавита. Со-

ставим всевозможные пары и запишем их в табл. 8.2 с соответст-

вующими вероятностями (найденными как произведения вероят-

ностей отдельных символов, поскольку символы независимы).

Согласно построенному дереву код Хаффмена для указанных

групп содержит следующие кодовые комбинации:

00;

011;

010.