Васюков В.Н. Теория электрической связи

Подождите немного. Документ загружается.

8.5. Помехоустойчивое кодирование

253

ром символе имела место ошибка, декодер может ее исправить,

прибавив (по модулю 2) к ошибочному символу единицу. Поэтому

код Хэмминга принадлежит к кодам, исправляющим ошибки, или

корректирующим.

Границы корректирующей способности кода Хэмминга иллю-

стрируются следующим примером.

Пример 8.9. Предположим, что при передаче разрешенной ко-

довой комбинации 0100111 произошли две ошибки, скажем, в

третьем и пятом символах, так что принята комбинация 0110011.

Найдем синдром:

   

1 0 1

111

1 1 0

0 1 1 0 0 1 1 0 1 0

0 1 1

1 0 0

0 1 0

0 0 1











Синдром указывает на 6-й символ, как на ошибочный. Таким

образом, в случае двукратной ошибки факт ошибки обнаруживает-

ся (синдром оказывается ненулевым), но исправить ее нельзя, так

как синдром оказывается таким же, как в случае однократной

ошибки в другом символе. Итак, код Хэмминга (7,4) обнаруживает

одно- и двукратные ошибки и исправляет однократные. ◄

Помехоустойчивость рассмотренного кода Хэмминга просто

объясняется с геометрической точки зрения. Легко убедиться, что

расстояние между любыми двумя разрешенными комбинациями

этого кода не менее 3. Поэтому при приеме запрещенной комбина-

ции она заменяется той разрешенной комбинацией, расстояние до

которой равно 1. Двукратная ошибка отдаляет принимаемую ком-

бинацию на расстояние, равное 2, что и приводит к ошибочному

«исправлению» ошибки. При этом «исправляется» один символ,

поэтому «исправленная» комбинация отстоит от принятой на рас-

стояние 1.

Коды, обнаруживающие ошибки, но не исправляющие их, мо-

гут использоваться в системах с решающей обратной связью (сис-

темах с переспросом [10]). В таких системах при обнаружении

ошибки во время декодирования по каналу обратной связи переда-

ется сигнал переспроса, и тогда передающее устройство повторяет

передачу забракованной комбинации.

8. ОСНОВЫ ТЕОРИИ ИНФОРМАЦИИ

254

В заключение отметим, что при решении вопроса о целесооб-

разности помехоустойчивого кодирования и выборе помехоустой-

чивого кода следует руководствоваться критерием скорости переда-

чи информации при заданной достоверности. Дело в том, что

введение избыточных символов приводит к увеличению времени

передачи кодовой комбинации или к укорочению элементарных по-

сылок, что ведет к повышению вероятности ошибочного приема

символа. Поэтому применение помехоустойчивого кодирования или

некоторого конкретного кода может оказаться нецелесообразным.

8.6. ИНФОРМАТИВНОСТЬ НЕПРЕРЫВНЫХ

ИСТОЧНИКОВ СООБЩЕНИЙ

Наряду с дискретными источниками сообщений часто встре-

чаются непрерывные источники, которые вырабатывают сообще-

ния, обычно описываемые функциями, принимающими значения

из непрерывного множества. Ярким примером непрерывного со-

общения является речевое сообщение, описываемое вещественной

функцией непрерывного времени. Значение непрерывного сооб-

щения в некоторый отдельный момент времени представляет со-

бой непрерывную случайную величину

, описываемую функцией

распределения

 

()F x x

Ρ

где – реализация случайной величины

, или плотностью рас-

пределения

( ) ( )/w x dF x dx

Очевидно, введенное ранее понятие энтропии неприменимо к

непрерывному источнику, так как неопределенность относительно

любого конкретного значения непрерывной случайной величины

равна бесконечности.

Действительно, разобьем область определения непрерывной

случайной величины

( , ) 

на отрезки одинаковой длины

пронумеруем их при помощи индекса

,i   

. Поставим в соот-

ветствие каждому отрезку значение



, равное его середине, и ве-

роятность

()



, равную вероятности попадания в данный интер-

вал исходной непрерывной случайной величины

. Таким образом

получается дискретная случайная величина, которая тем точнее

описывает непрерывную случайную величину, чем меньше интер-

вал

8.6. Информативность непрерывных источников сообщений

255

Для этой дискретной случайной величины можно записать эн-

тропию

( ') ( ' )log ( ' )

H X P x P x









Подставив вместо вероятности

( ' )

ее приближенное значе-

ние

( ' )

w x x

, получим в пределе при

0x 

 

( ) lim ( ') lim ( ' ) log ( ' )

H X H X w x x w x x









   







 

lim ( ' )log ( ' ) lim ( ' )log

i i i

w x w x x w x x x





 

   

    

   

   



 

( )log ( ) lim log

w x w x dx x







    



Из полученного выражения следует, что энтропия непрерывно-

го распределения равна бесконечности за счет второго слагаемого,

которое одинаково для всех непрерывных распределений, задан-

ных на интервале

( , ) 

. «Индивидуальность» распределения

определяется первым слагаемым, которое и используют в качестве

меры информативности непрерывного источника и называют от-

носительной, или дифференциальной энтропией

( ) ( )log ( )h X w x w x dx









Дифференциальная энтропия, в отличие от энтропии дискрет-

ного источника, самостоятельного смысла не имеет и служит для

сравнения информативности различных непрерывных источников

между собой [10].

Пример 8.10. Дифференциальная энтропия источника, описы-

ваемого гауссовской плотностью вероятности

 

()

w x e





равна

( ) ( )log ( ) ( )log

()

h X w x w x dx w x dx



 

   



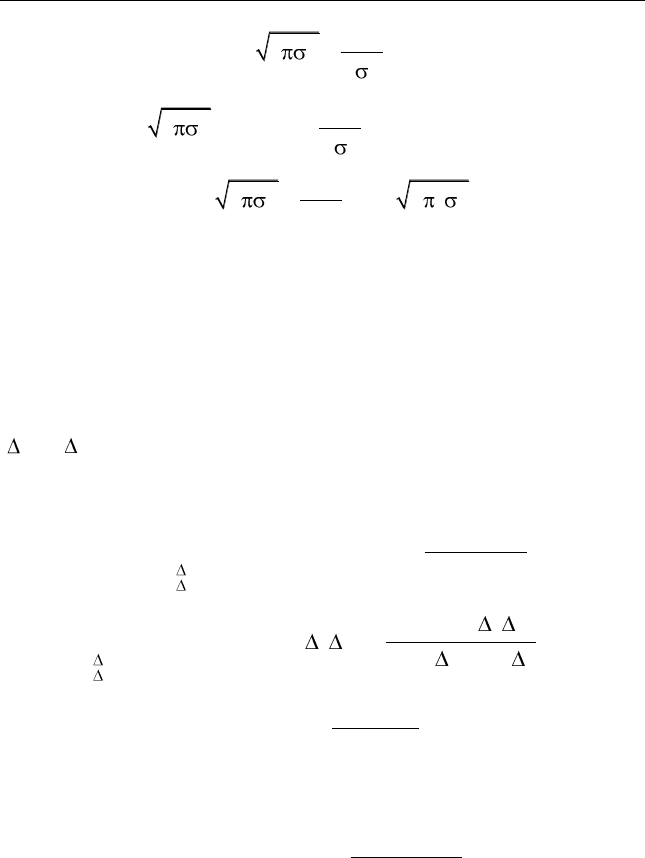
8. ОСНОВЫ ТЕОРИИ ИНФОРМАЦИИ

256

 

log

( ) log 2

w x x m dx







   







 

log

log 2 ( ) ( )

w x dx x m w x dx



 

   



log

log 2 log 2

e  

Отметим, что дифференциальная энтропия нормального рас-

пределения не зависит от математического ожидания и она тем

больше, чем больше дисперсия. Это вполне соответствует понима-

нию дифференциальной энтропии как меры неопределенности, ко-

торая, очевидно, возрастает с ростом дисперсии случайной вели-

чины. ◄

Определим взаимную информацию двух непрерывных случай-

ных величин

. Разобьем области их значений на интервалы

, перейдем к дискретным случайным величинам



после чего воспользуемся формулой (8.7) и выполним предельный

переход:

( , )

( , ) lim ( , )log

( ) ( )

p x y

I X Y p x y

p x p y





 

















( , )

lim ( , ) log

( ) ( )

w x y x y

w x xw y y





 

















( , )

( , )log

( ) ( )

w x y

w x y dxdy

w x w y



 





Полученное выражение можно переписать следующим обра-

зом:

( ) ( | )

( , ) ( , )log

( ) ( )

w y w x y

I X Y w x y dxdy

w x w y



 





( , )log ( ) ( , )log ( | )w x y w x dxdy w x y w x y dxdy

   

   

   

   

( ) ( | )h X h X Y

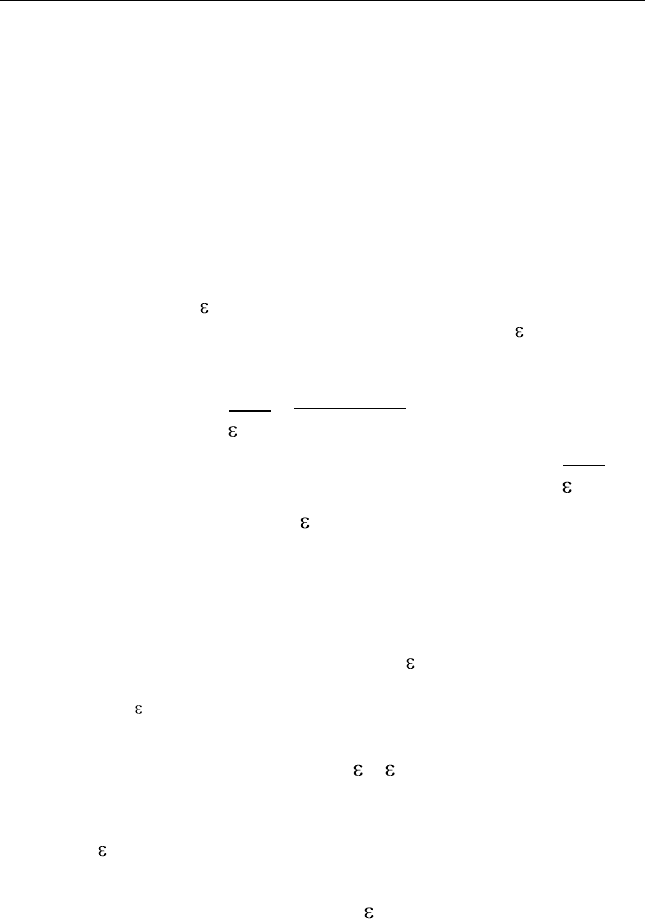
8.6. Информативность непрерывных источников сообщений

257

где

( | ) ( , )log ( | )h X Y w x y w x y dxdy



 





– условная дифферен-

циальная энтропия.

Эпсилон-энтропия. Энтропия источника непрерывных сооб-

щений, как было показано, равна бесконечности. Это означает по

существу то, что для передачи непрерывного сообщения с абсо-

лютной (бесконечной) точностью необходимо передать бесконеч-

ное количество информации. В то же время ясно, что на практике

это и не требуется, так как любой получатель сообщений обладает

ограниченной разрешающей способностью: достаточно воспроиз-

вести сообщение с конечной точностью, характеризуемой некото-

рым малым числом . При этом количество передаваемой инфор-

мации оказывается конечным и зависит от параметра . В качестве

критерия можно использовать, например, средний квадрат разно-

сти между принятым

()xt



и переданным

()xt

сообщениями

 

( ) ( ) ( )t x t x t





При этом сообщения считаются эквивалентными, если

()t

не

превосходит заданного уровня

Средняя взаимная информация между

()xt



()xt

 

( , ) ( | )I X X h X h X X





зависит не только от свойств сообщения

()xt

, которыми определя-

ется дифференциальная энтропия, но и от . Величина

( ) min ( , ) ( ) max ( | )H X I X X h X h X X



  

, (8.12)

где минимум выбирается по всем возможным условным распреде-

лениям

 

|w x x



, для которых



, называется эпсилон-

энтропией. Это минимальное количество информации в сообщении

()xt



о сообщении

()xt

при условии, что они эквиваленты в смысле

критерия .

Положим

( ) ( ) ( )X t X t t





тогда условная дифференциальная энтропия

( | )h X X



при извест-

ном

()xt



полностью определяется дифференциальной энтропией

8. ОСНОВЫ ТЕОРИИ ИНФОРМАЦИИ

258

()h

отсчета шума воспроизведения

()t

. При этом

 

max | maxh X X h





. Поскольку мощность шума воспроизве-

дения ограничена значением

, очевидно, что дифференциальная

энтропия

()h

максимальна, когда отсчет

()t

– гауссовская слу-

чайная величина с нулевым средним, и это максимальное значение

равно

max ( ) log 2he

. (8.13)

Подставляя это выражение в (8.12), получим

( ) ( ) log 2H X h X e



Эпсилон-энтропия максимальна для гауссовского источника с

дисперсией

( ) log 2 log 2 log

H X e e  

. (8.14)

8.7. ПРОПУСКНАЯ СПОСОБНОСТЬ

НЕПРЕРЫВНОГО КАНАЛА С АДДИТИВНЫМ

БЕЛЫМ ГАУССОВСКИМ ШУМОМ

Пусть колебание

()zt

на выходе непрерывного канала пред-

ставляет собой сумму сигнала

()xt

и шума

()t

( ) ( ) ( )z t x t t

, (8.15)

причем сигнал и шум статистически независимы. Предположим,

что канал имеет полосу частот, ограниченную частотой

, и дей-

ствует в течение временного интервала

. Тогда согласно теореме

отсчетов каждый процесс, входящий в выражение (8.15), может

быть представлен совокупностью

2M F T

отсчетов. Совокуп-

ность отсчетов сигнала, которую можно представить вектором

, ,...,

x x xx 

, имеет совместную плотность распределения веро-

ятностей

( ) ( , ,..., )

w w x x xx 

; статистические свойства шумово-

го вектора

, ,...,

ξ

описываются совместной ПРВ

 

( ) , ,...,

wwξ

8.7. Пропускная способность непрерывного канала…

259

Пропускную способность непрерывного канала определим как

()

lim max ( , )

C I X Z





, (8.16)

где

( , )I X Z

– количество информации о реализации сигнала

()xt

длительности

, содержащееся (в среднем) в реализации процесса

()zt

той же длительности (максимум ищется среди всевозможных

распределений

()w x

Средняя взаимная информация сигнала и наблюдаемого про-

цесса равна

( , ) ( ) ( | )I X Z h Z h Z X

. (8.17)

С учетом (8.15) условная плотность распределения вероятности

( | ) ( )wwzx ξ

, а условная дифференциальная энтропия

( | ) ... ( , )log ( | ) ( )h Z X w w d hz x z x z



 

  



, (8.18)

где – обозначение векторной случайной величины, составлен-

ной из шумовых отсчетов. Таким образом, с учетом (8.16), (8.17) и

(8.18) пропускная способность непрерывного канала с аддитивным

шумом

 

()

lim max ( ) ( )

C h Z h





. (8.19)

Пример 8.11. Рассмотрим пропускную способность непрерыв-

ного канала с аддитивным квазибелым гауссовским шумом,

имеющим одностороннюю спектральную плотность мощности

в полосе частот от 0 до

. Отсчеты шума статистически незави-

симы, и дифференциальная энтропия

 

к к к ш

( ) 2 log 2 log 2 log 2h F T e F T e F T eP  

, (8.20)

где

ш 0 к

P N F



– мощность (дисперсия) шума.

Дифференциальная энтропия

()

случайной величины

максимальна, если

– гауссовская случайная величина с нулевым

средним, а это означает, что

– тоже гауссовская случайная ве-

личина с нулевым средним. Дифференциальная энтропия совокуп-

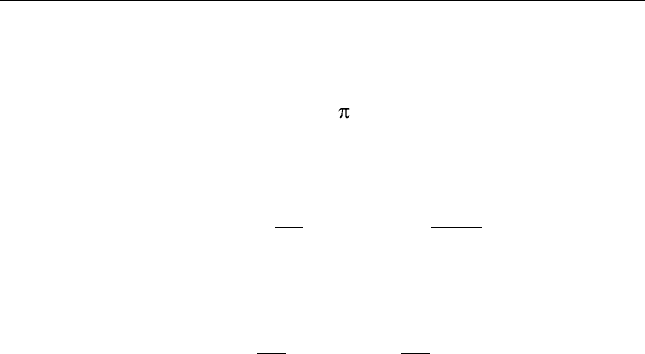
8. ОСНОВЫ ТЕОРИИ ИНФОРМАЦИИ

260

ности отсчетов максимальна, если отсчеты статистически незави-

симы (это выполняется, так как отсчеты квазибелого шума некор-

релированные гауссовские, а значит, независимые), тогда

 

к c ш

( ) log 2 ( )h Z F T e P P

. (8.21)

Подставляя (8.21) и (8.20) в (8.19), получаем формулу Шеннона

для пропускной способности непрерывного канала с АБГШ [10]:

кк

ш к 0

log 1 log 1

C F F

P F N



   





. (8.22)

При расширении полосы пропускания пропускная способность

непрерывного канала с АБГШ стремится к пределу

log 1,443





КОНТРОЛЬНЫЕ ВОПРОСЫ

1. В чем состоит цель экономного кодирования?

2. Что такое избыточность дискретного источника?

3. Какой источник обладает минимальной избыточностью и

чему равна его энтропия?

4. Может ли равномерный код быть оптимальным (безызбы-

точным)?

5. В результате применения процедуры экономного кодирова-

ния получился троичный код с вероятностями символов 0.5, 0.2 и

0.3 соответственно. Можно ли считать такой код оптимальным?

6. Можно ли применять коды, для которых префиксное прави-

ло не выполняется?

7. Может ли помехоустойчивый код быть безызбыточным?

8. На чем основано корректирующее свойство помехоустойчи-

вых кодов?

9. Что такое кодовое расстояние?

10. В какой связи находятся порождающая и проверочная мат-

рицы линейного кода?

11. Какой геометрический смысл имеют строки порождающей

матрицы?

12. Какова размерность линейного пространства, натянутого на

строки порождающей матрицы? Каково количество разрешенных

комбинаций кода? Каково количество запрещенных комбинаций?

13. Что такое синдром?

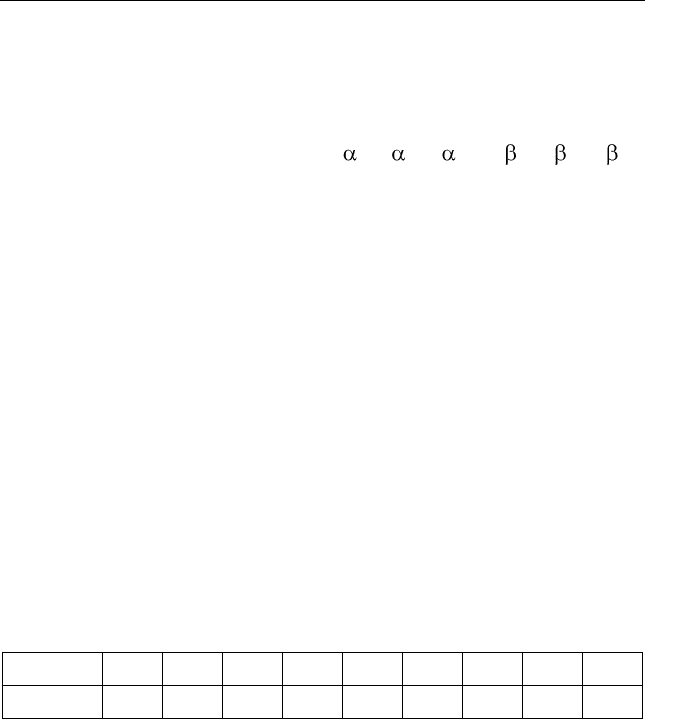
Упражнения

261

УПРАЖНЕНИЯ

1. Рассчитайте для частных случаев, указанных в конце примера

8.2, а также для

0.25pp

условную энтропию согласно (8.4).

2. Даны источники с алфавитами, содержащими по три символа

и с распределениями вероятностей

1 2 3

1/ 3 1/ 3 1/3

1 2 3

1/ 2 1/ 4 1/ 4

Найдите энтропии источников.

3. Имеются два дискретных источника с матрицами









1 2 3

y y y

q q q









(верхняя строка матрицы

содержит символы, нижняя – их вероятности). Определите, какой

источник обладает большей неопределенностью в случае, если:

а)

pp

1 2 3

q q q

; б)

pq

2 2 3

p q q

4. По каналу связи передается один из двух символов

или

с одинаковыми вероятностями. На выходе они преобразуются в

символы

, причем из-за помех в среднем два символа из ста

принимаются неверно. Определите среднее количество информа-

ции на один символ, передаваемое по такому каналу. Сравните с

аналогичной величиной при отсутствии помех.

5. Марковский источник сообщений вырабатывает символы

с вероятностями

0,4

0,5

0,1

соответственно. Вероят-

ности появления пар заданы таблицей

( , )

P x x

0,1

0,2

0,1

0,2

0,3

0,1

Определите энтропию источника и сравните ее с энтропией ис-

точника без памяти с такими же вероятностями символов.

Указание. Энтропия марковского источника первого порядка

при объеме алфавита

находится по формуле

( ) ( , )log ( | )

j i i j

H X P x x P x x







6. Две двоичные случайные величины

имеют совмест-

ные вероятности

( 0) ( 0, 1) ( 1) 1/3P x y P x y P x y        

Найдите

()HX

()HY

( | )H X Y

( | )H Y X

( , )H X Y

8. ОСНОВЫ ТЕОРИИ ИНФОРМАЦИИ

262

7. Сообщения

появляются на выходе источ-

ника с вероятностями 1/2, 1/4, 1/8 и 1/8. Постройте двоичный код

Шеннона – Фано и определите вероятности символов 0 и 1, а также

среднюю длину кодового слова.

8. Источник вырабатывает два независимых символа

с вероятностями 0,9 и 0,1 соответственно. Постройте коды Хаф-

фмена для отдельных символов и групп по два символа. Найдите и

сравните для двух полученных кодов:

− среднюю длину кодового слова,

− избыточность кода,

− вероятность появления символа 0 (1) в кодовой последова-

тельности,

− скорость передачи информации (длительность посылки

примите равной 1 мкс).

9. Для условий упражнения 8 постройте код Хаффмена для

групп по три символа. Найдите среднюю длину кодового слова,

избыточность кода, вероятность появления символа 0 (1) в кодовой

последовательности и скорость передачи информации. Сравните с

аналогичными показателями для случая кодирования отдельных

символов и групп по два символа.

10. Найдите две разрешенные кодовые комбинации кода Хэм-

минга (7, 4), не совпадающие со строками порождающей матрицы,

и убедитесь в том, что расстояние между ними не менее трех.

11. Измените в одной из комбинаций два символа, найдите

синдром и «исправьте» в принятой комбинации символ, на кото-

рый он укажет. Найдите расстояние между «исправленной» и при-

нятой комбинациями.

12. Код Хэмминга (7, 4) обнаруживает одно- и двукратные

ошибки и исправляет однократные. Считая, что ошибки при прие-

ме двоичных посылок независимы и происходят с вероятностью

, найдите вероятность появления двукратной ошибки в пределах

7-разрядной кодовой комбинации. Найдите вероятность появления

не более чем одной ошибки.