Васюков В.Н. Теория электрической связи

Подождите немного. Документ загружается.

3.3. Корреляционно-спектральная теория cлучайных процессов

123

Пример 3.6. Белый шум. Так называется стационарный случай-

ный процесс с нулевым средним, имеющий АКФ вида

( ) )



Очевидно, что в этом случае СПМ постоянна на всех частотах

от



до



( ) /2

W f N

(Принято использовать обозначение

/2N

для двусторонней

СПМ; односторонняя обозначается

Легко видеть, что никакой реальный случайный процесс не

может быть белым шумом, так как белый шум имеет бесконечную

дисперсию (мощность). Кроме того, для белого шума теряет смысл

понятие распределения. Однако эта модель чрезвычайно удобна в

анализе вследствие -образности АКФ, поэтому она широко ис-

пользуется.◄

Пример 3.7. Квазибелый шум (шум, белый в ограниченной по-

лосе частот от

F

до

), рис. 3.7, а. Такой процесс имеет СПМ

вида

0 в

/ 2 при ,

()

0 в противном случае.

N f F











АКФ квазибелого шума согласно теореме Винера – Хинчина

имеет вид

в0

sin(2 )

( ) cos(2 )

R f df F N







показанный на рис. 3.7, б. Особенность такого процесса заключа-

ется в том, что график его АКФ пересекает ось времени в точках,

кратных

 

1/ 2F

. Таким образом, дискретизация квазибелого шума

/2N

()

R()

а б

Рис. 3.7. СПМ (а) и АКФ (б) квазибелого шума

3. СЛУЧАЙНЫЕ ПРОЦЕССЫ

124

с шагом

 

1/ 2

TF

дает последовательность некоррелированных

случайных величин. В частности, если квазибелый шум является

гауссовским процессом, то его отсчеты, взятые с шагом

, оказы-

ваются независимыми, что упрощает анализ (см., например,

разд. 9.3).◄

3.4. ВОЗДЕЙСТВИЕ СТАЦИОНАРНЫХ

СЛУЧАЙНЫХ ПРОЦЕССОВ НА ЛИС-ЦЕПИ

Рассматривая воздействие стационарного (здесь и далее – в

широком смысле) случайного процесса на ЛИС-цепь в рамках кор-

реляционно-спектральной теории, достаточно интересоваться

только моментами не выше второго порядка. Отсюда следует, что

при воздействии ССП

()xt

на ЛИС-цепь с КЧХ

()Hf

и импульс-

ной характеристикой

()ht

можно ставить задачу найти среднее

значение (математическое ожидание) и АКФ выходного процесса

()yt

, а также взаимно корреляционные функции

()

процессов

()xt

()yt

В задаче анализа ЛИС-цепи при стационарном случайном воз-

действии в качестве входного процесса обычно рассматривается

процесс с нулевым средним. Если математическое ожидание вход-

ного процесса (постоянное вследствие стационарности) отлично от

нуля,

m 

, всегда можно рассмотреть прохождение через ЛИС-

цепь постоянной и флюктуационной составляющих отдельно. Оче-

видно, математическое ожидание выходного процесса

(0)

m H m

. Далее полагаем, что на вход цепи с КЧХ

()Hf

воз-

действует стационарный процесс

()xt

с нулевым средним и АКФ

( ) ( )

R W f e df











Каждая реализация

()t

процесса

()yt

получается сверткой

реализации

()t

процесса

()xt

с импульсной характеристикой

ЛИС-цепи, или, что то же самое, обратным преобразованием Фу-

рье произведения КЧХ цепи

()Hf

на спектральную плотность

()f

входной реализации

()t

( ) ( ) ( )

j ft

t H f t e dt e df







 











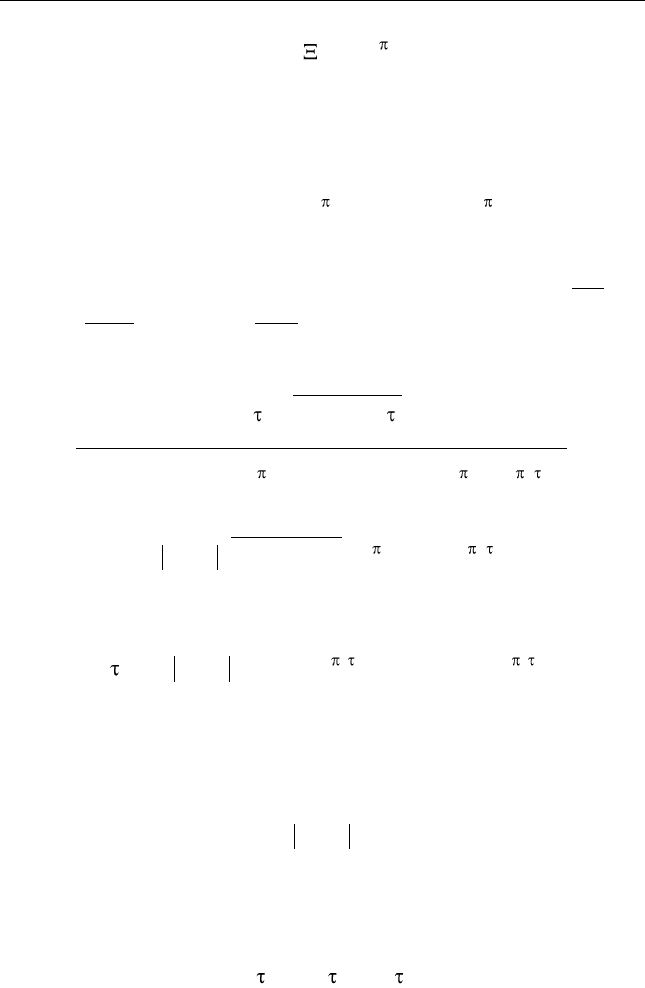
3.4. Воздействие стационарных случайных процессов на ЛИС-цепи

125

( ) ( )

j ft

H f f e df











(Здесь, как и в разд. 3.4, следует иметь в виду, что интеграл в фи-

гурных скобках в классическом смысле расходится.)

Переходя от реализаций к процессам, можно записать

( ) ( ) ( ) ( )

j ft j ft

y t H f X f e df Y f e df





 





где

()Yf

– случайная функция частоты (тот же случайный про-

цесс, представленный в другом «базисе»). Заметим, что из

( ) 0xt 

следует

( ) 0Xf

и далее

( ) 0Yf

Автокорреляционная функция процесса

()yt

( ) ( ) ( )

R y t y t  

* * 2

1 1 1

( ) ( ) ( ) ( )

j f t j f

j ft

H f X f e df H f X f e e df







 





2 ( ) 2

( ) ( ) ( )

j f f t j f

H f X f X f e e dfdf



  

 





Учитывая (3.9), запишем

( ) ( ) ( ) ( )

j f j f

y x y

R H f W f e df W f e df





 





Из последнего выражения следует, что отклик ЛИС-цепи на

стационарный случайный процесс имеет спектральную плотность

мощности, равную входной СПМ, умноженной на квадрат модуля

КЧХ (т. е. на квадрат АЧХ) цепи:

( ) ( ) ( )

W f H f W f

. (3.12)

Это выражение описывает спектральный метод анализа ЛИС-цепей

при случайных стационарных воздействиях.

Поскольку частотные функции в (3.12) умножаются, соответст-

вующие временные функции взаимодействуют путем свертки

( ) ( ) ( )

y h x

R R R

3. СЛУЧАЙНЫЕ ПРОЦЕССЫ

126

Здесь временнáя функция

()

соответствует спектральной плот-

ности мощности

()

входного процесса, а

2 * 2

( ) ( ) ( ) ( )

j f j f

R H f e df H f H f e df





 





. (3.13)

Заметим, что

()Hf

– преобразование Фурье импульсной ха-

рактеристики

()ht

, вещественной по предположению. Тогда

()Hf

соответствует функции

()ht

. Действительно, согласно

теореме обращения (см. п. 2.10.2)

( ) ( )h t H f  

, а для вещест-

венных функций

( ) ( )H f H f

. Умножению частотных функций

в правой части выражения (3.13) соответствует свертка их времен-

ных прообразов, поэтому

( ) ( ) ( ) ( ) ( )

R h h h t h t d





    



и функцию

()

можно назвать автокорреляционной функцией

импульсной характеристики

. АКФ импульсной характеристики

может быть измерена при помощи коррелометра, подключенного к

выходу цепи, если на ее вход подать белый шум с единичной спек-

тральной плотностью мощности. Действительно, при этом

( ) ( )

R 

, следовательно,

( ) ( )

RR

Взаимно корреляционная функция входного и выходного про-

цессов

( ) ( ) ( )

R x t y t  

1 1 1

( ) ( ) ( )

j f t j f

j ft

X f e df H f X f e e df







 





2 ( ) 2

1 1 1

( ) ( ) ( )

j f f t j f

H f X f X f e e dfdf



  

 





Заметим, что здесь имеется в виду АКФ детерминированной функции.

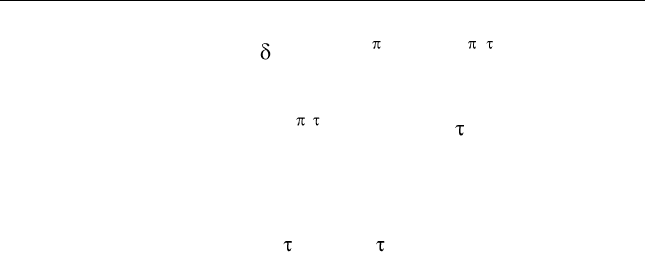
3.5. Безынерционные нелинейные преобразования случайных процессов

127

2 ( ) 2

1 1 1

( ) ( ) ( )

j f f t j f

H f W f f f e e dfdf



  

 

  



( ) ( ) ( ) ( )

H f W f e df h t R t dt





 

  



Для ВКФ входного и выходного процессов выполняется свой-

ство

( ) ( )

xy yx

RR

Анализ распределения шума на выходе цепи в общем случае

весьма сложен, однако во многих практически важных случаях вы-

ходной процесс можно считать гауссовским. Это предположение

оправдано, когда:

1) эффективная ширина спектра входного процесса намного

шире, чем полоса пропускания цепи (при этом происходит норма-

лизация процесса, так как интеграл Дюамеля можно приближенно

представить суммой независимых «прошлых» отсчетов входного

процесса с весовыми коэффициентами, равными соответствующим

отсчетам импульсной характеристики, причем количество этих не-

зависимых отсчетов равно отношению длины ИХ к интервалу кор-

реляции входного процесса, или, что то же самое, отношению по-

лосы частот входного процесса к полосе пропускания цепи;

согласно центральной предельной теореме Ляпунова распределе-

ние суммы независимых случайных величин стремится к нормаль-

ному с увеличением числа слагаемых);

2) на входе ЛИС-цепи гауссовский процесс, причем необяза-

тельно широкополосный (при этом значение выходного процесса

равно сумме гауссовских случайных величин, которая имеет гаус-

сово распределение независимо от числа слагаемых) .

3.5. БЕЗЫНЕРЦИОННЫЕ НЕЛИНЕЙНЫЕ

ПРЕОБРАЗОВАНИЯ

СЛУЧАЙНЫХ ПРОЦЕССОВ

Ранее рассматривались линейные преобразования детермини-

рованных колебаний и случайных процессов. Напомним, что ли-

нейными называются преобразования, подчиняющиеся принципу

суперпозиции (см. разд. 2). В технике связи часто используются

цепи, не удовлетворяющие этому принципу, т.е. нелинейные.

3. СЛУЧАЙНЫЕ ПРОЦЕССЫ

128

К сожалению, общей теории нелинейных цепей и их взаимодейст-

вия с сигналами, столь же простой, как теория ЛИС-цепей, не су-

ществует. Некоторые задачи, связанные с воздействием детерми-

нированных колебаний на нелинейные цепи, будут рассмотрены в

разд. 5. Анализ многомерного распределения шума на выходе не-

линейной цепи в общем случае представляет собой крайне слож-

ную задачу, однако иногда рассматриваемая нелинейная цепь яв-

ляется безынерционной

, т. е. значение выходного процесса

зависит только от значения входного процесса в этот же момент

времени. Кроме того, во многих практически важных задачах дос-

таточно знать распределение процесса лишь в одном временно´м

сечении, т. е. его одномерное распределение (распределение мгно-

венного значения случайного процесса). Таким образом, фактиче-

ски при этом рассматривается нелинейное преобразование случай-

ной величины, анализ которого представляет собой сравнительно

простую задачу.

Нелинейная безынерционная цепь описывается характеристи-

кой

()y f x

, указывающей зависимость мгновенного значения

выходного процесса

()yt

от мгновенного значения

входного

процесса

()xt

. Предположим, что эта зависимость монотонна,

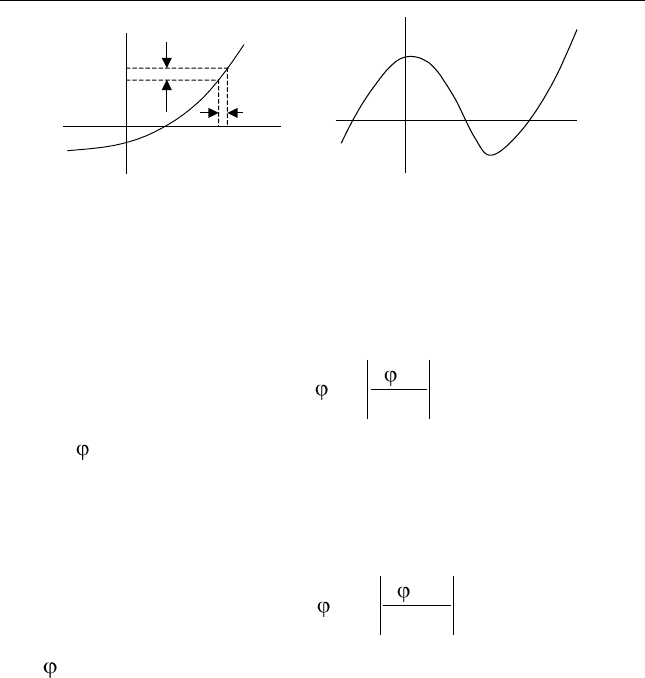
(рис. 3.8, а). Обозначим одномерную ПРВ мгновенного значения

входного процесса

()

, а аналогичную функцию для выходного

процесса –

()

(индексы указывают, к какой случайной величи-

не относится соответствующая ПРВ). Поскольку вероятность по-

падания случайной величины

с плотностью

()

в бесконечно

узкий интервал

( , )x x dx

равна

()

w x dx

и при этом с такой же

вероятностью случайная величина

попадает в интервал

( , )y y dy

, при любом

и соответствующем

выполняется

равенство

( ) ( )

w x dx w y dy

Формально отсюда следует равенство

( ) ( )

w y w x



Можно сказать, что безынерционная цепь не имеет памяти.

3.6. Узкополосные случайные процессы

129

а б

Рис. 3.8. К формулам (3.14), (3.15)

но нужно учесть, во-первых, что правая часть, как и левая, должна

зависеть только от

, и, во-вторых, что ПРВ не может быть отри-

цательной. С учетом сказанного можно записать

 

()

( ) ( )

w y w y



, (3.14)

где

()xy

– функция, обратная по отношению к характеристике

()f 

нелинейной безынерционной цепи.

Если характеристика цепи не является монотонной и содержит

участков монотонности (рис. 3.8, б,

3N 

), то формула (3.14)

приобретает вид

 

()

( ) ( )

y x k

w y w y





, (3.15)

где

()

– функция, обратная к характеристике нелинейной цепи

на

-м участке монотонности.

3.6. УЗКОПОЛОСНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ

Представление, аналогичное аналитическому сигналу, суще-

ствует и для случайных процессов. Оно особенно удобно для опи-

сания узкополосных случайных процессов. Узкополосные СП иг-

рают чрезвычайно важную роль в теории связи, так как они

описывают модулированные сигналы, переносящие информацию,

а также узкополосные (сосредоточенные по спектру) помехи, часто

имеющие место в каналах связи.

Предположим, что на вход цепи, изображенной на рис. 2.32, б,

поступает стационарный в широком смысле случайный процесс

3. СЛУЧАЙНЫЕ ПРОЦЕССЫ

130

()xt

со спектральной плотностью мощности

()

. Поскольку

АЧХ фильтра Гильберта тождественно равна 1, СПМ сопряженно-

го процесса

()xt

, которую обозначим

()

, равна

()

. Зна-

чит, равны и автокорреляционные функции этих процессов:

( ) ( )

RR

. (3.16)

Рассмотрим комплексный СП

( ) ( ) ( )z t x t j x t  

. (3.17)

Поскольку он формируется фильтром с КЧХ (2.62), его СПМ

должна быть равна

4 ( ), 0,

()

0, 0.

W f f













Согласно теореме Винера – Хинчина АКФ комплексного СП

( ) 4 ( )

R W f e df









4 ( )cos(2 ) 4 ( )sin(2 )

W f f df j W f f df



  



. (3.18)

Заметим, что в силу четности СПМ вещественного процесса

()xt

его АКФ

( ) 2 ( )cos(2 )

R W f f df







Тогда

( ) 2 ( ) 2 ( )

R R j R



  

, (3.19)

где для мнимой части (3.18) введено обозначение

2 ( )R

Вспомним, что спектральная плотность аналитического сигна-

ла является правосторонней (равна 0 при отрицательных частотах).

Так как АКФ и СПМ комплексного случайного процесса

()zt

так-

же связаны парой преобразований Фурье, то очевидно, что право-

сторонней СПМ должна соответствовать АКФ, имеющая вид ана-

литического сигнала, причем ее вещественная и мнимая части

связаны парой преобразований Гильберта:

( ) ( ) ( )

re imz

R R jR

. (3.20)

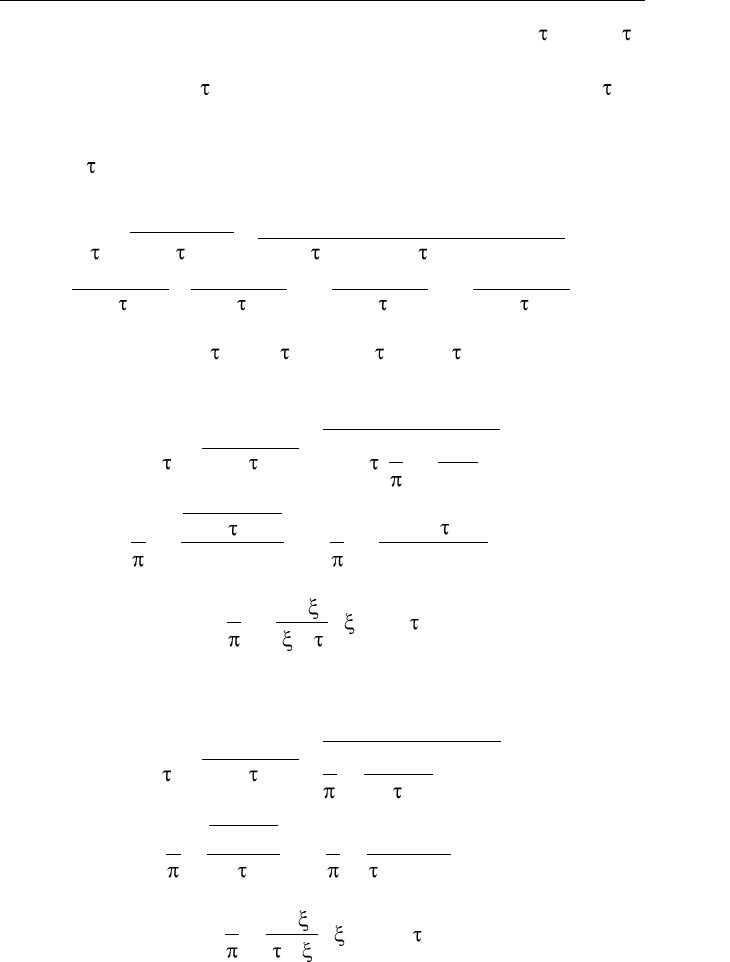
3.6. Узкополосные случайные процессы

131

Сравнивая (3.20) и (3.19), видим, что функция

( ) 2 ( )

re x

RR

является четной вещественной (это видно и из выражения (3.18),

определяющего

()

суммой косинусоид). Аналогично

()

–

вещественная нечетная функция, как сумма синусоид, каждая

из которых сопряжена по Гильберту соответствующей косинусои-

де в

()

Запишем АКФ комплексного СП

()zt

ˆˆ

( ) ( ) ( ) [ ( ) ( )][ ( ) ( )]

R z t z t x t j x t x t j x t

         

ˆ ˆ ˆ ˆ

( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )x t x t x t x t j x t x t j x t x t          

ˆ ˆ ˆ

( ) ( ) [ ( ) ( )]

x x xx xx

R R j R R   

. (3.21)

Найдем слагаемые мнимой части:

1 ( )

( ) ( ) ( ) ( )

R x t x t x t ds





    





()

1 ( ) ( ) 1

R t s

x t x s

ds ds

t s t s



 





  





()











Полученное выражение представляет функцию, сопряженную

по Гильберту автокорреляционной функции исходного процесса.

1 ( )

( ) ( ) ( ) ( )

R x t x t ds x t





    





()

1 ( ) ( ) 1

()

R s t

x s x t

ds ds

t s s t



 



  

   



()





  





3. СЛУЧАЙНЫЕ ПРОЦЕССЫ

132

Таким образом, слагаемые мнимой части отличаются только

знаком; учитывая это, а также тот факт, что

( ) ( )

RR

[см.

(3.16)], запишем на основании (3.21)

( ) 2 ( ) 2 ( )

x xxz

R R j R  

Еще раз отметим, что вещественная часть АКФ комплексного

СП

()zt

является четной, а мнимая – нечетной функциями. В част-

ности, отсюда следует, что случайные процессы, сопряженные по

Гильберту, некоррелированны в совпадающие моменты времени

(при

0

Все сказанное справедливо для любого комплексного случай-

ного процесса

()zt

, определенного выражением (3.17) (необяза-

тельно узкополосного). Если же процесс является узкополосным,

то для него характерно наличие некоторой средней частоты и мед-

ленно меняющейся огибающей (комплексной). Типичный вид

мнимой и вещественной частей АКФ комплексного узкополосного

СП приведен на рис. 3.9. Характерными особенностями являются

их колебательный характер, симметрия огибающих, а также оди-

наковая частота квазигармонического заполнения.

Модель комплексного случайного процесса используется при

нахождении плотности распределения вероятностей огибающей

узкополосного гауссовского случайного процесса, которая необхо-

дима, в частности, для анализа качества приема (демодуляции) ам-

плитудно-модулированных сигналов на фоне шума. Подробно за-

дача оптимального приема сигналов в присутствии помех

рассматривается в разд. 9.

Предположим, что

()xt

– гауссовский узкополосный СП с

нулевым средним (это предположение на практике обычно выпол-

няется, так как случайный процесс на входе демодулятора пред-

ставляет собой результат полосовой фильтрации входного широ-

кополосного шума, а при этом происходит его нормализация [8]).

()



а б

Рис. 3.9. Вещественная и мнимая части АКФ комплексного СП