Ваган В.А. и др. Физика. В 3 ч. Часть 1. Механика. Молекулярная физика и термодинамика: Пособие для студентов вузов

Подождите немного. Документ загружается.

Ваган В.А., Конкин Б.Б., Сафронов В.П.

ФИЗИКА

Часть I

2009

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение

высшего профессионального образования

Ростовская-на-Дону государственная академия

сельскохозяйственного машиностроения

Ваган В.А., Конкин Б.Б., Сафронов В.П.

КУРС ФИЗИКИ

В трех частях

Часть

первая

Механика.

Молекулярная физика и термодинамика

Утверждено редакционно-издательским советом академии

в качестве конспекта лекций

для студентов вузов всех технических специальностей

Ростов-на-Дону

2009

УДК 537.8

Ф48

Рецензенты:

доктор технических наук, профессор

Донского государственного технического университета

Ю.И. Ермольев

кандидат физико-математических наук, доцент

Ростовской-на-Дону государственной академии

сельскохозяйственного машиностроения

В.А. Ваган

Физика. В 3 ч. Ч. I. Механика. Молекулярная

физика и термодинамика: Пособие для студен-

тов вузов. / Авт.-сост. В.А.Ваган, Б.Б. Конкин,

В.П. Сафронов, РГАСХМ ГОУ, Ростов н/Д.,

2009. — 82 с.

Даны основные понятия, положения, зависимости, формулы,

графики к разделам «Механика. Молекулярная физика и термоди-

намика» курса физики.

Предназначено для студентов технических вузов.

Материал изложен в соответствии с утвержденной учебной программой

высшего профессионального образования

Ростовская-на-Дону государственная академия

сельскохозяйственного машиностроения, 2009

Ф48

КИНЕМАТИКА

ЧАСТЬ 1

МЕХАНИКА

изучает закономерности механического движения.

Механическое движение — изменение взаимного расположения

тел с течением времени.

Глава 1

КИНЕМАТИКА

изучает движение тел, не рассматривая причины этого движения.

1.1. Кинематические уравнения движения материальной точки

♦ Материальная точка

— тело, размерами которого можно пре-

небречь в данной задаче (размеры тел намного меньше расстоя-

ний между ними или тело движется поступательно, т.е. все точки

тела описывают одинаковые траектории).

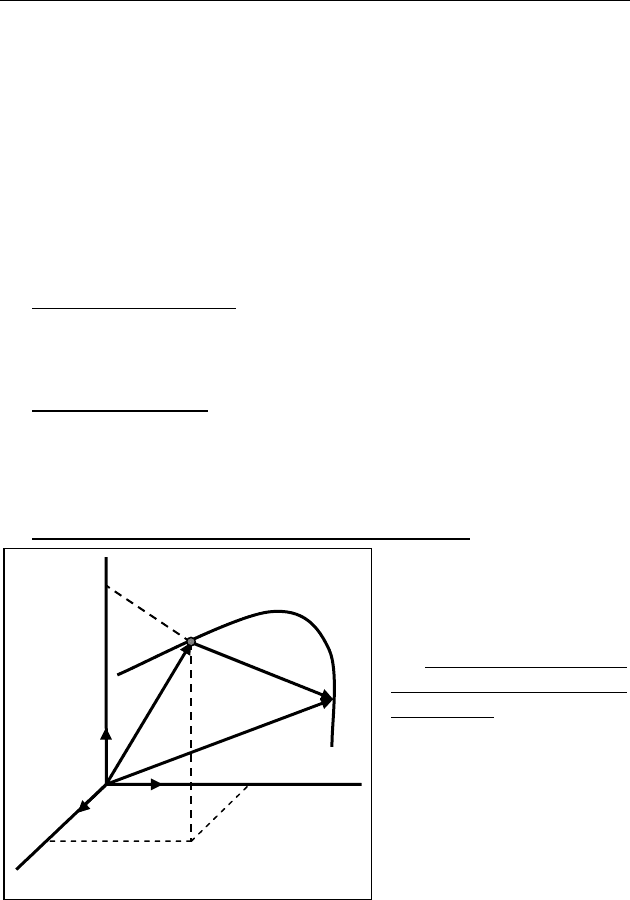
♦ Система отсчета

включает тело отсчета (относительно кото-

рого рассматривается движение), связанную с ним систему коор-

динат (рис. 1.) и способ отсчета времени (часы). Система отсчета

выбирается для определения положения материальной точки (те-

ла) в пространстве и времени.

♦ Относительность механического движения

заключается в

зависимости координат,

траектории, скорости и

ускорения тела от выбо-

ра системы отсчета.

♦ Положение матери-

альной точки в про-

странстве задается ука-

занием координат

111

,,xyz точки M, ли-

бо значением радиус-

вектора

, проведенно-

го в точку М из начала

координат (точка

0).

Причем,

11 1 1

rxiyjzk

⋅+ ⋅+ ⋅

Рис. 1

КИНЕМАТИКА

где

111

,,xyz — координаты точки, ,,ijk⋅

— единичные век-

торы (орты) осей

,,xyz

(рис. 1). Модуль радиус-вектора нахо-

дится по теореме Пифагора:

222

11 1 11

||rr x yz

=++

♦ Траектория — линия, по которой движется тело.

♦ Перемещение

rrr

−

=Δ — приращение радиус-вектора за

рассматриваемый промежуток времени.

♦ Путь

Δ ,м — расстояние, пройденное движущейся точкой за

рассматриваемый промежуток времени вдоль траектории (рис. 1).

♦ Дуговая координата s ,м — длина участка траектории, прой-

денного движущейся точкой в течение рассматриваемого проме-

жутка времени.

♦ Кинематические уравнения движения — это зависимость ра-

диус-вектора

(или координат ,,xyz) от времени t (с), позво-

ляющая определить положение материальной точки при ее

движении в любой момент времени:

()rrt=

или (), (), ()xxt yyt zzt

==.

Эти две формы связаны принципом суперпозиции движений: лю-

бое сложное движение в пространстве можно представить как

сумму трех независимых прямолинейных движений вдоль осей

,,xyz:

() () () ()rt xt i yt j zt k=⋅+⋅+⋅

1.2. Скорость

♦ Математика.

Средней скоростью изменения функции

()ft называется отно-

шение приращения функции

к приращению аргумента tΔ :

ср

Мгновенной, истинной скоростью изменения

()ft называется

предел, к которому стремится средняя скорость при

→

. Это

скорость в заданный момент

времени:

lim

fdf

tdt

Δ→

===

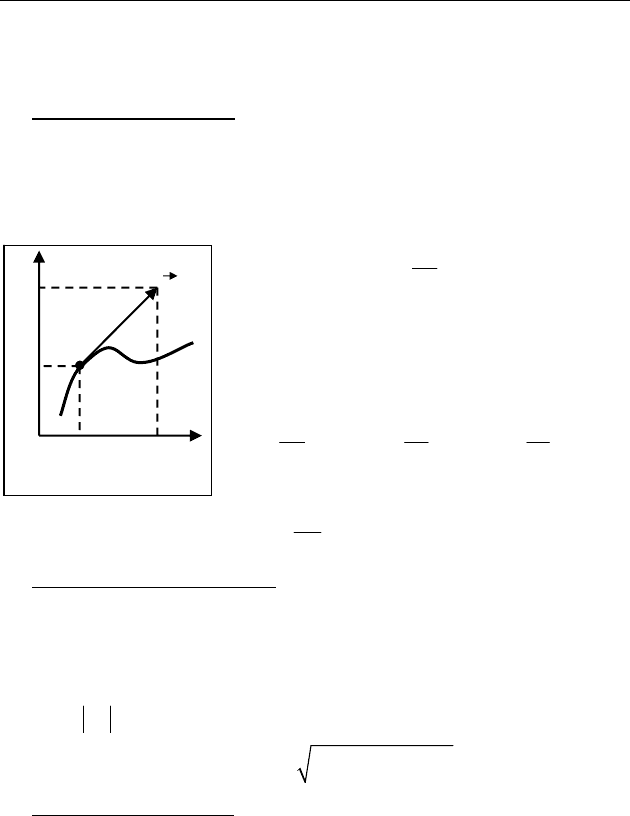
КИНЕМАТИКА

Таким образом, чтобы определить скорость изменения функции,

нужно взять производную этой функции по времени

Скорость определяет быстроту изменения функции.

♦ Скорости движения определяют быстроту движения. При

движении материальной точки

,{ , , },rxyzs

становятся функциями

от времени:

(), { (), (), ()}, ()rrt xxt yyt zzt SSt=====

Поэтому, вводится три типа скоростей:

Векторная скорость (просто скорость)

, м/с — равна

и направлена по касательной к траекто-

рии (рис. 2

Проекции

на оси координат определяют

быстроту изменения координат точки

///

xyz

ttt

dx dy dz

xyz

dt dt dt

=====vvv.

Скалярная скорость

,м/с:

=v .

♦

Связи между скоростями.

Дифференцируя принцип суперпозиции, получаем:

() () () ()rt xt i yt j zt k

′′ ′ ′

=⋅+⋅+⋅⇒

xy z

() () () ()ttitjtk=⋅+⋅+⋅vv v v

Так как dr dS=

, ||

. Из теоремы Пифагора

222

|()| ()

xyz

tt== ++vv vvv

♦ Сложение скоростей.

Если тело в выбранной системе отсчета одновременно участвует

в нескольких движениях со скоростями

12 n

, ...vv v

, то его ско-

рость

равна векторной сумме этих скоростей:

Рис. 2

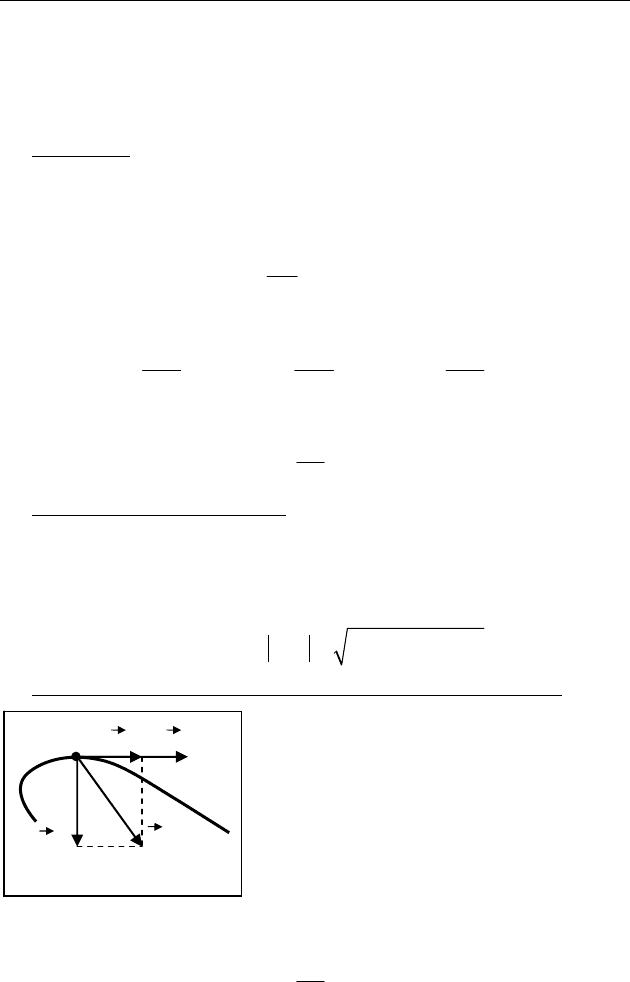
КИНЕМАТИКА

Этот закон является следствием инвариантности перемещений и

интервалов времени в разных системах отсчета в классической

(ньютоновской) механике.

1.3. Ускорение

♦ Ускорение ,a

м/с

— определяет быстроту изменения скоро-

сти (скорость изменения скорости). Аналогично скоростям вво-

дятся следующие типы ускорений:

Векторное ускорение (просто ускорение)

м/с

′

===

Проекции ускорения

на оси координат:

xyz

axayaz

dt dt dt

′

′′′′′

== == ==

Тангенциальное ускорение ,a

м/с

′

♦ Связи между ускорениями.

Дифференцируя принцип суперпозиции два раза, получаем:

xy z

() ( ) ( ) ( )tijk

′′′

=⋅+⋅+⋅⇒vʹ vvv

xy z

() () () ()at a t i a t j a t k=⋅+⋅+⋅

По теореме Пифагора:

222

xyz

()at a a a=++

♦ Тангенциальная и нормальная составляющие ускорения.

В общем случае, ускорение

может

быть направлено под любым углом к

скорости

. Поэтому его удобно

представить как векторную сумму

двух ускорений (рис. 3):

aa a

— тангенциальное ускорение на-

правлено по (против) скорости и определяет быстроту изменения

модуля скорости материальной точки:

′

Рис. 3

КИНЕМАТИКА

— нормальное (центростремительное) ускорение направлено

перпендикулярно скорости и определяет быстроту изменения на-

правления скорости материальной точки:

где

r — радиус кривизны траектории (радиус окружности, по кото-

рой двигалась бы материальная точка при

1.4. Равнопеременное движение

При таком движении aconst

, то есть модуль скорости за рав-

ные промежутки времени изменяется на одинаковые величины.

Если

0aconst

=>, движение называется равноускоренным, а

если

0aconst

— равнозамедленным. Если

0aaconsta

== =, то движение будет равнопеременное

прямолинейное. Определим в этом случае скорость и кинемати-

ческое уравнение движения.

♦

Скорость.

По определению

aa d adt

⋅

== ⇒

rr rr

. Выберем ось 0Х

вдоль направления движения, тогда в проекциях на эту ось

dadt⋅v= . Проинтегрируем это выражение:

xx1x11x

()t a dt c a dt c c a t+= +=+⋅

∫∫

v= .

Если 0t

, то

(0) cv=, значит

x0xx

()tat=+vv

где

v — проекция начальной скорости на ось 0Х.

♦

Кинематическое уравнение движения.

По определению

ddt

⋅

=⇒vx=v.

Проинтегрируем это выражение:

x20x 2

() ( )

tdtc adtc

t c

+=⋅⋅

⋅

⋅+

∫∫

x=v v

КИНЕМАТИКА

Если 0t = , то

(0)xc= , значит

(

)

⋅

⋅+x=x+v

где

(0)

=x — начальная координата.

При

равномерном прямолинейном движении, когда 0a

, полу-

чаем

x0x

()tconst==vv

()

⋅

=x +v .

♦

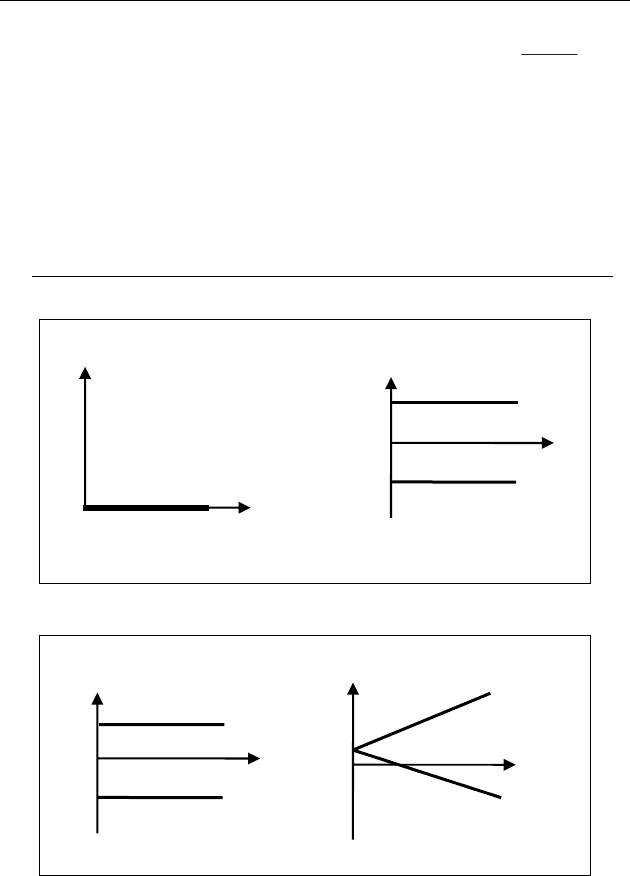
Графическое представление кинематических характеристик

Графики ускорения

Графики скорости

Рис. 5а

Равномерное

Равнопеременное

Рис. 5б

Рис. 4а

Равномерное

Равнопеременное

Рис. 4б

a=0

КИНЕМАТИКА

Кинематическое уравнение движения

1.5. Кинематика вращательного движения твердого тела

Абсолютно твердым (твердым) называется тело, для которого

расстояние между любыми двумя его точками всегда остается

неизменным. Любое движение твердого тела можно представить

в виде комбинации

поступательного и вращательного движе-

ний. При поступательном движении траектории любых точек

тела одинаковы, поэтому оно эквивалентно движению матери-

альной точки. При

вращательном движении все точки движутся

по концентрическим окружностям, центры которых лежат на од-

ной прямой, называемой осью вращения

(ОО׳ рис. 7).

♦ Элементарный поворот d

— мера перемещения тела во

вращательном движении. По модулю он равен углу поворота dϕ

и ориентирован вдоль оси вращения

OO׳ (рис. 7). Его

направление определяется правилом правого винта (для правой

системы координат, см. рис. 1), или правилом левого винта (для координат, см. рис. 1), или правилом левого

винта (для левой системы координат, в кото-

рой оси 0Х и 0Y меняются местами). Векто-

ра, имеющие разное направление в разных

системах координат, называются псевдовек-

торами.

♦

Угловая координата

, рад — определя-

ет положение тела при вращательном дви-

жении.

♦

Кинематическое уравнение движения

()tϕ=ϕ — позволяет определить положение тела в любой мо-

мент времени.

Рис. 6а

Равномерное Равнопеременное

Рис. 6б

dϕ

Рис. 7