Тырсин А.Н. Теория вероятностей и математическая статистика. Учебное пособие

Подождите немного. Документ загружается.

181

ЗАДАЧИ КОНТРОЛЬНОЙ РАБОТЫ

Задача 1. Случайные события

1. Из 20 сбербанков 10 расположены за чертой города. Для обследования

случайным образом отобрано 5 сбербанков. Какова вероятность того, что среди

отобранных окажется в черте города: а) три сбербанка; б) хотя бы один?

2. Вероятность хотя бы одного попадания стрелком при двух выстрелах

равна 0,96. Найти вероятность трех попаданий при четырех выстрелах.

3. Наудачу взятый телефонный номер состоит из 5 цифр. Какова вероят-

ность того, что в нем все цифры: а) различные; б) одинаковые; в) нечетные?

Известно, что номер телефона не начинается с цифры ноль.

4. Для проведения соревнования 16 волейбольных команд разбиты по жре-

бию на две подгруппы (по восемь команд в каждой). Найти вероятность того,

что две наиболее сильные команды окажутся: а) в разных подгруппах; б) в од-

ной подгруппе.

5. Студент знает 20 из 25 вопросов программы. Зачет считается сданным,

если студент ответит не менее чем на 3 из 4 поставленных в билете вопросов.

Взглянув на первый вопрос билета, студент обнаружил, что он его знает. Како-

ва вероятность того, что студент: а) сдаст зачет; б) не сдаст зачет?

6. В старинной игре в, кости необходимо было для выигрыша получить при

бросании трех игральных костей сумму очков, превосходящую 10. Найти веро-

ятности: а) выпадения 11 очков; б) выигрыша.

7. Экспедиция издательства отправила газеты в три почтовых отделения.

Вероятность своевременной доставки газет в первое отделение равна 0,95, во

второе отделение − 0,9 и в третье − 0,8. Найти вероятность следующих собы-

тий: а) только одно отделение получит газеты вовремя; б) хотя бы одно отделе-

ние получит газеты с опозданием.

8. В озере было отловлено 100 карпов. Их пометили и отпустили обратно в

озеро. Затем поймали 500 карпов, из которых оказалось помеченными 60 рыб.

Сколько приблизительно карпов в водоеме?

9. На связке 5 ключей. К замку подходит только один ключ. Найти вероят-

ность того, что потребуется не более двух попыток открыть замок, если опро-

бованный ключ в дальнейших испытаниях не участвует.

182

10. Имеются 5 столбиков и 8 ведер с красками разных цветов. Каждый

столбик окрашивается краской из наудачу взятого ведра (при этом может полу-

читься так, что разные столбики будут окрашены одной и той же краской).

Найти вероятность того, что все столбики будут окрашены разными красками.

Задача 2. Дискретные случайные величины

11. Компания производит пружины, 10% из которых оказываются брако-

ванными. Сто пружин отобраны для контроля качества. Требуется найти ожи-

даемое количество бракованных пружин и стандартное отклонение бракован-

ных в отобранных образцах, а также вероятность того, что в выборке, по мень-

шей мере, 10 бракованных пружин.

12. Два стрелка сделали по два выстрела по мишени. Вероятность попада-

ния в мишень для первого стрелка равна 0,6, для второго

−

0,7. Необходимо:

а) составить закон распределения общего числа попаданий; б) найти математи-

ческое ожидание и дисперсию этой случайной величины.

13. В среднем по 10% договоров страховая компания выплачивает страхо-

вые суммы в связи с наступлением страхового случая. Составить закон распре-

деления числа таких договоров среди наудачу выбранных четырех. Вычислить

математическое ожидание и дисперсию этой случайной величины.

14. В билете три задачи. Вероятность правильного решения первой задачи

равна 0,9, второй – 0,8, третьей – 0,7. Составить закон распределения числа

правильно решенных задач в билете и вычислить математическое ожидание и

дисперсию этой случайной величины.

15. Вероятность попадания в цель при одном выстреле равна 0,8 и умень-

шается с каждым, выстрелом на 0,1. Составить закон распределения числа по-

паданий в цель, если сделано три выстрела. Найти математическое ожидание,

дисперсию и среднее квадратическое отклонение этой случайной величины.

16. Найти закон распределения числа пакетов трех акций, по которым вла-

дельцем будет получен доход, если вероятность получения дохода по каждому

из них равна соответственно 0,5, 0,6, 0,7. Найти математически ожидание и

дисперсию данной случайной величины построить функцию распределения.

17. Экзаменатор задает студенту вопросы, пока тот правильно отвечает.

Как только число правильных ответов достигнет четырех либо студент ответит

неправильно, экзаменатор прекращает задавать вопросы. Вероятность правиль-

ного ответа на один вопрос равна 2/3. Составить закон распределения числа за-

данных студенту вопросов.

183

18. Каждый поступающий в институт должен сдать 3 экзамена. Вероят-

ность успешной сдачи первого экзамена 0,9, второго – 0,8, третьего – 0,7. Сле-

дующий экзамен абитуриент сдает только в случае успешной сдачи предыду-

щего. Составить закон распределения числа экзаменов, сдававшихся абитури-

ентом. Найти математическое ожидание этой случайной величины.

19. Из поступивших в ремонт 10 часов 7 нуждаются в общей чистке меха-

низма. Часы не рассортированы по виду ремонта. Мастер, желая найти часы,

нуждающиеся в чистке, рассматривает их поочередно и, найдя такие часы, пре-

кращает дальнейший просмотр. Составить закон распределения числа просмот-

ренных часов. Найти математическое ожидание и дисперсию этой случайной

величины.

20. Производители карманных калькуляторов знают из опыта работы, что

1% произведенных и проданных калькуляторов имеют дефекты и их должны

заменить по гарантии. Фирма купила 500 калькуляторов. Какова вероятность,

что пять или больше калькуляторов нужно будет заменить?

Задача 3. Непрерывные случайные величины

21. В нормально распределенной совокупности 15% значений x меньше 12

и 40% значений x больше 16,2. Найти среднее значение и стандартное отклоне-

ние данного распределения.

22. Время изготовления детали – равномерно распределенная случайная

величина на отрезке [4, 8] мин. Изготовлено пять деталей. Какова вероятность,

что время изготовления каждой из пяти деталей отклоняется от среднего не бо-

лее чем на 0,5 мин.?

23. Случайная величина распределена по закону равнобедренного тре-

угольника в интервале (–1, 1) (закону Симпсона). Написать выражение для

плотности распределения вероятностей. Вычислить функцию распределения

вероятностей, математическое ожидание, дисперсию, моду, коэффициент экс-

цесса.

24. Текущая цена акции может быть смоделирована с помощью нормаль-

ного закона распределения с математическим ожиданием 15 ден. ед. и средним

квадратическим отклонением 0,2 ден. ед.

1. Найти вероятность того, что цена акции: а) не выше 15,3 ден. ед.; б) не

ниже 15,4 ден. ед.; в) от 14,9 до 15,3 ден. ед.

2. С помощью правила трех сигм найти границы, в которых будет нахо-

диться текущая цена акции.

184

25. Цена некой ценной бумаги нормально распределена. В течение послед-

него года 20% рабочих дней она была ниже 88 ден. ед., а 75% – выше 90 ден.

ед.

Найти: а) математическое ожидание и среднее квадратическое отклонение

цены ценной бумаги; б) вероятность того, что в день покупки цена будет за-

ключена в пределах от 83 до 96 ден. ед.; в) с надежностью 0,95 определить мак-

симальное отклонение цены ценной бумаги от среднего (прогнозного) значения

(по абсолютной величине).

26. Коробки с конфетами упаковывает автомат. Их средняя масса равна 540

г. Известно, что 5% коробок имеют массу, меньшую 500 г. Каков процент ко-

робок, масса которых: а) менее 470 г; б) от 500 до 550 г; в) более 550 г; г) отли-

чается от средней не более чем на 30 г (по абсолютной величине)?

27. Вес упаковки чипсов, производимых некоторой фирмой, подчиняется

нормальному закону распределения, средний вес упаковки составляет 375 г.,

отклонение от среднего веса равно25 г.

Найти вероятность того, что в выпущенной партии чипсов вес одной упа-

ковки будет: а) от 300 до 425 г., б) не более 450 г., в) больше 300г.

28. 20%-ная точка нормально распределенной случайной величины равна

50, а 40%-ная точка равна 35. Найти вероятность того, что случайная величина

примет значение в интервале (25; 45).

29. Квантиль уровня 0,15 нормально распределенной случайной величины

X равен 12, а квантиль уровня 0,6 pавен 16. Найти математическое ожидание и

среднеквадратическое отклонение случайной величины.

30. Манометр показывает давление в колонне. Давление колеблется от 10,0

до 10,2 атм., и в этих пределах любое давление равновозможно. Вследствие по-

вреждения манометра его стрелка не отклоняется больше чем на 10,16 атм. Ка-

кое давление в среднем показывает манометр?

Задача 4. Совместное распределение случайных величин

31. Найти коэффициент корреляции ρ(X, X + Y), где X и Y независимы и

распределены по стандартному нормальному закону.

32. Случайная величина X имеет равномерное распределение на [1, 2]. Най-

ти функции распределения и плотности случайной величины Y = 2X + 1.

33. Закон распределения двумерной дискретной случайной величины (X, Y)

задан таблицей

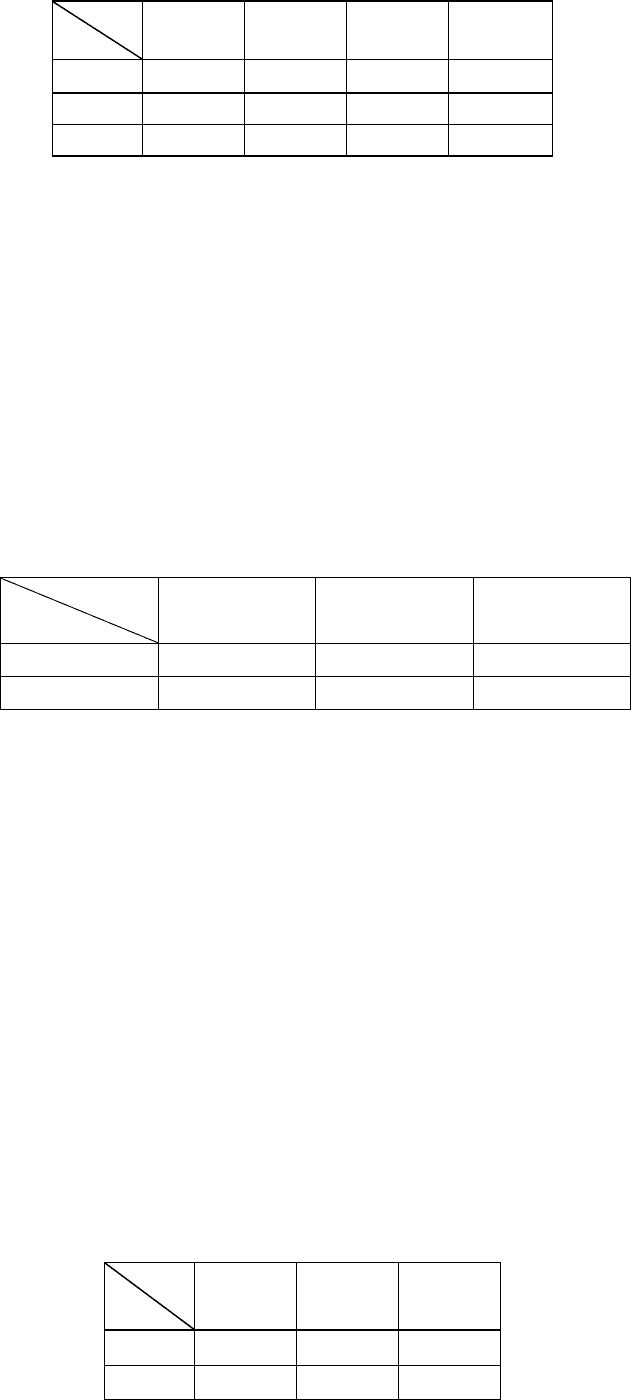
185

0 1 2 3

−1

0,02 0,03 0,09 0,01

0 0,04 0,20 0,16 0,10

1 0,05 0,10 0,15 0,05

Найти: а) законы распределения одномерных случайных величин X и Y; б)

условные законы распределения случайной величины Х при условии Y = 2 и

случайной величины Y при условии X = 1; в) вероятность P(Y > X).

34. Задана функция распределения двумерной случайной величины (X,Y)

F(x, y) = (1 − e

−x

)(1 − e

−y

); x ≥ 0, y ≥ 0.

Найти вероятность того, что в результате испытания составляющие X и Y при-

мут значения соответственно Х < 1, Y < 3.

35. Закон распределения двумерной дискретной случайная величины (X, Y)

задан таблицей:

-1 0 1

1 0,15 0,3 0,35

2 0,05 0,05 0,1

Найдите законы распределения составляющих X и Y. Вычислите вероятности

Р(Х = 2, Y = 0); Р(Х > Y). Установите, зависимы или нет составляющие Х и Y.

36. Рассматривается двумерная случайная величина (X, Y), где X − поставка

сырья, Y − поступление требования на него. Известно, что поступление сырья и

поступление требования на него могут произойти в любой день месяца (30

дней) с равной вероятностью. Определить:

а) выражение совместной плотности и функции распределения двумерной слу-

чайной величины (X,Y);

б) плотности вероятности и функции распределения одномерных составляю-

щих X и Y;

в) зависимы или независимы X и Y.

37. Дискретное совместное распределение случайного вектора (X,

Y) зада-

ется таблицей:

−1

0 1

−1

1/8 1/12 7/24

1 5/24 1/6 1/8

Найти: а) одномерные законы распределения X и Y; б) закон распределе-

ния X + Y; в) закон распределения Z = Y

38. Найти коэффициент корреляции , где случайная величина X

имеет показательное распределение с параметром λ = 1.

),(

XXρ

39. Случайная величина X имеет равномерное распределение на [0, 1]. Най-

ти плотность вероятности случайной величины Y = X

и ее математическое

ожидание.

40. Найти закон распределения суммы двух независимых случайных вели-

чин, каждая из которых распределена по стандартному нормальному закону,

т.е. N(0; 1).

Задача 5. Закон больших чисел и предельные теоремы

41. Среднее изменение курса акции компании в течение одних биржевых

торгов составляет 0,3%. Оценить вероятность того, что на ближайших торгах

курс изменится более чем на 3%.

42. Отделение банка обслуживает в среднем 100 клиентов день. Оценить

вероятность того, что сегодня в отделении банка будет обслужено: а) не более

200 клиентов; б) более 150 клиентов.

43. Вероятность того, что акции, переданные на депозит, будут востребо-

ваны, равна 0,08. Оценить с помощью неравенства Чебышева вероятность того,

что среди 1000 клиентов от 70 до 90 востребуют свои акции.

44. Вероятность угадывания 6 номеров в спортлото (6 из 49) равна 7,2⋅10

-8

При подсчете оказались заполненными 5 млн. карточек. Какова вероятность,

что никто не угадал все 6 номеров? Какое наименьшее количество карточек

нужно заполнить, чтобы с вероятностью не менее 0,9 хотя бы один угадал 6

номеров?

45. Бензоколонка N заправляет легковые и грузовые автомобили. Вероят-

ность того, что проезжающий легковой автомобиль подъедет на заправку, равна

0,3. С помощью неравенства Чебышева найти границы, в которых с вероятно-

стью, не меньшей 0,79, находится доля заправившихся в течения 2 часов легко-

вых автомобилей, если за это время всего заправилось 100 автомобилей.

46. В среднем 10% работоспособного населения некоторого региона – без-

работные. Оценить с помощью неравенства Чебышева вероятность того, что

уровень безработицы среди обследованных 10000 работоспособных жителей

города будет в пределах от 9 до 11 % (включительно).

186

47. Выход цыплят в инкубаторе составляет в среднем 70% числа заложен-

ных яиц. Сколько нужно заложить яиц, чтобы с вероятностью, не меньшей 0,95,

ожидать, что отклонение числа вылупившихся цыплят от математического

ожидания их не превышало 50 (по абсолютной величине)? Решить задачу с по-

мощью: а) неравенства Чебышева; б) интегральной теоремы Муавра-Лапласа.

48. Опыт работы страховой компании показывает, что страховой случай

приходится примерно на каждый пятый договор. Оценить с помощью неравен-

ства Чебышева необходимое количество договоров, которые следует заклю-

чить, чтобы с вероятностью 0,9 можно было утверждать, что доля страховых

случаев отклонится от 0,1 не более чем на 0,01 (по абсолютной величине).

Уточнить ответ с помощью интегральной теоремы Муавра-Лапласа.

49. Урожайность куста картофеля задается следующим распределением:

Урожай в кг 0 1 1,5 2 2,5

Вероятность 0,1 0,2 0,2 0,3 0,2

На участке высажено 900 кустов. В каких пределах с вероятностью 0,95

будет находиться урожай? Какое наименьшее число кустов нужно посадить,

чтобы с вероятностью не менее 0,975 урожай был не менее тонны?

50. Известно, что дисперсия каждой из данных независимых случайных

величин не превышает 4. Определить число таких величин, при котором веро-

ятность отклонения средней арифметической случайной величины от средней

арифметической их математических ожиданий не более чем на 0,25 превысит

0,99.

Задача 6. Выборочное оценивание

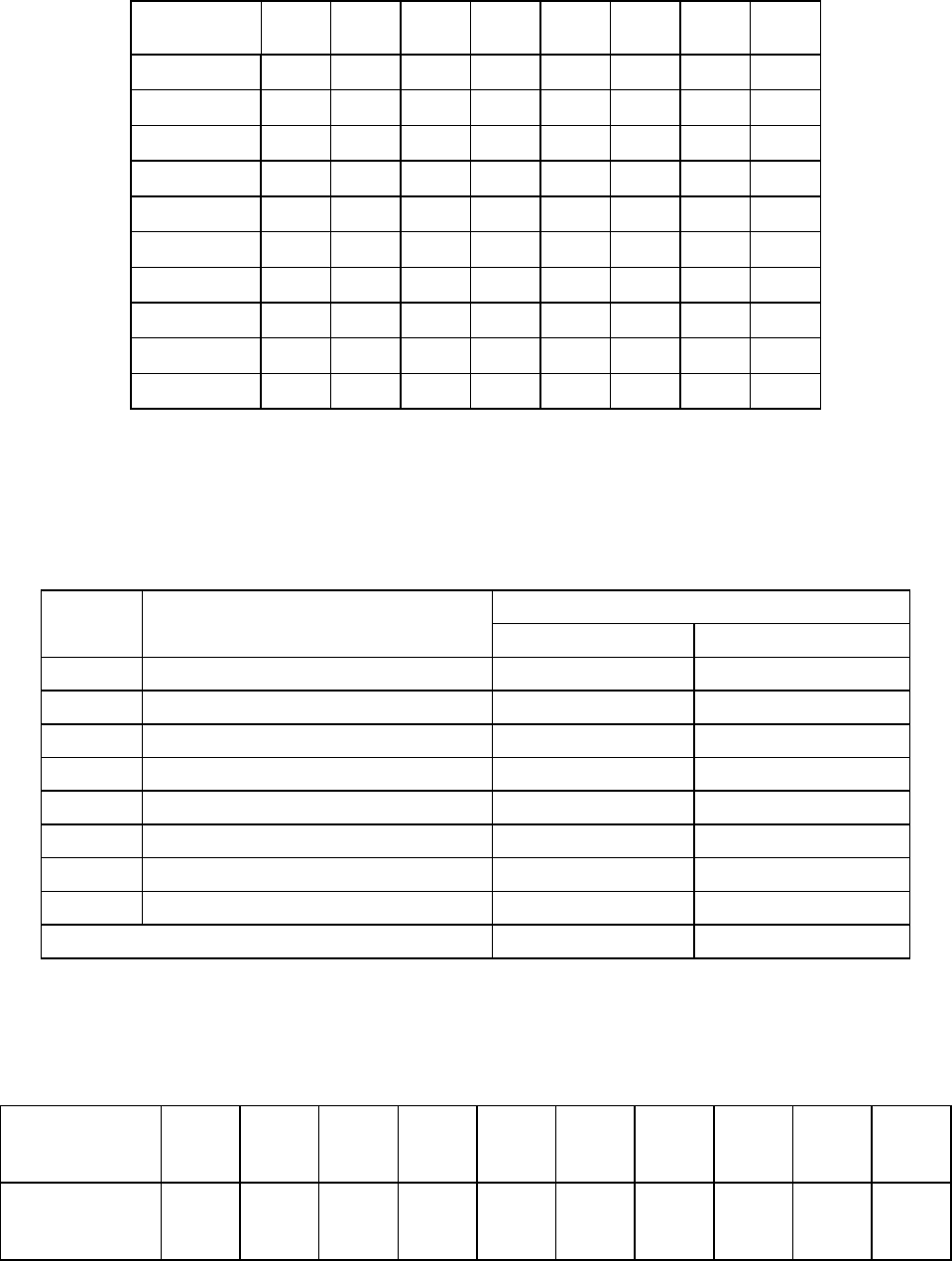
Выборочная проверка размеров дневной выручки оптовой базы от реализа-

ции товаров по 100 рабочим дням дала следующие результаты:

1 2 3 4 5 6

0–5 5–10 10–15 15–20 20–25 25–30 30–35 35–40

Здесь: i – номер интервала наблюденных значений дневной выручки (i = 1, … ,

8); J

– границы i – того интервала (в условных денежных единицах); n

– число

рабочих дней, когда дневная выручка оказывалась в пределах i- го интервала;

при этом, очевидно, что =

n = 100.

∑

Требуется:

- построитъ гистограмму частот;

187

188

- найти несмещенные оценки для математического ожидания и дисперсии

cлучайной величины

Х – дневной выручки оптовой базы;

- определить приближенно вероятность того, что в наудачу выбранный рабо-

чий день дневная выручка составит не менее 15 условных денежных единиц.

№

задач

51 3

16 20 23 20 6 4

52 2 9 14 17 25 22 7 4

53 4 7 15 20 24 22 5 3

54 3 8 15 19 26 20 6 3

55 4 6 8 18 24 20 14 6

56 3 4 9 19 23 20 12 10

57 3 6 8 18 21 22 14 8

58 2 5 9 17 23 20 15 9

59 2 3 8 18 24 22 13 10

60 1 7 10 16 23 20 14 9

Задача 7. Проверка статистических гипотез

61. Проверить по критерию Смирнова при уровне значимости α = 0,1 од-

нородность группированных выборок – выработки рабочих двух цехов.

Количество рабочих

№№

Выработка в отчетном году

в % к предыдущему

В первом цехе Во втором цехе

1 94 – 100 3 5

2 100 – 106 7 12

3 106 – 112 11 16

4 112 – 118 20 28

5 118 – 124 28 45

6 124 – 130 19 27

7 130 – 136 10 14

8 136 – 142 2 3

Всего 100 150

62. Даны результаты исследования отклонения фактического выпуска про-

дукции (тыс. руб.) от планового (план – 1000 тыс. руб.) 400 предприятий в

группированном виде:

Фактический

выпуск

950 –

960

960 –

970

970 –

980

980 –

990

990 –

1000

1000 –

1010

1010 –

1020

1020 –

1030

1030 –

1040

1040 –

1050

Количество

предприятий

5 15 60 72 80 60 55 30 20 3

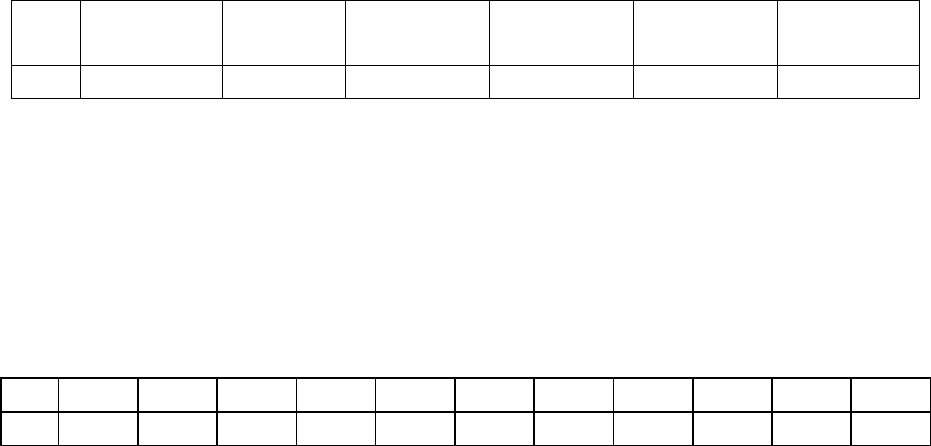
Проверить гипотезу о согласии эмпирического распределения с нормаль-

ной моделью по критерию χ

–Пирсона при α = 0,05.

63. Исследование длительности оборота оборотных средств двух групп

предприятий (по 14 предприятий в каждой) дало следующие результаты: сред-

негрупповые длительности оборота

дней,

дней; оценки диспер-

сий длительности оборота дней

, дней

. Выяснить, можно ли для

уровня значимости α = 0,1 считать, что отклонения в длительности оборота

оборотных средств у данных групп предприятий одинаковы.

64. Исследование в течение месяца (25 рабочих дней) ежедневных просто-

ев двух строительных бригад из-за отсутствия материалов дало следующие зна-

чения среднесуточных простоев:

75,1

ч.,

99,1

ч., при априорных пред-

положениях относительно дисперсий ч

4,1

=σ

., ч1,1

=σ

. Выяснить, можно

ли для уровня значимости α = 0,01 считать среднее время простоя бригад оди-

наковым.

65. Выборочное исследование возраста покупателей компакт-дисков в од-

ном из магазинов дало следующие результаты: 20, 20, 32, 27, 40, 24, 23, 18, 16,

15, 18, 26, 19,17, 19, 18, 23.

Проверить гипотезу о стохастической независимости элементов выборки

для уровня значимости α = 0,05 с помощью критериев «восходящих» и «нисхо-

дящих» серий.

66. Для исследования доходов населения города было отобрано 1000 жите-

лей. Получено следующее распределение жителей по месячному доходу (руб.):

менее 500 500-1000 1000-1500 1500-2000 2000-2500

Свыше

2500

58 96 239 328 147 132

Необходимо на уровне значимости 0,05 проверить гипотезу о нормальном

законе распределения признака (случайной величины)

X, используя критерий

согласия χ

–Пирсона.

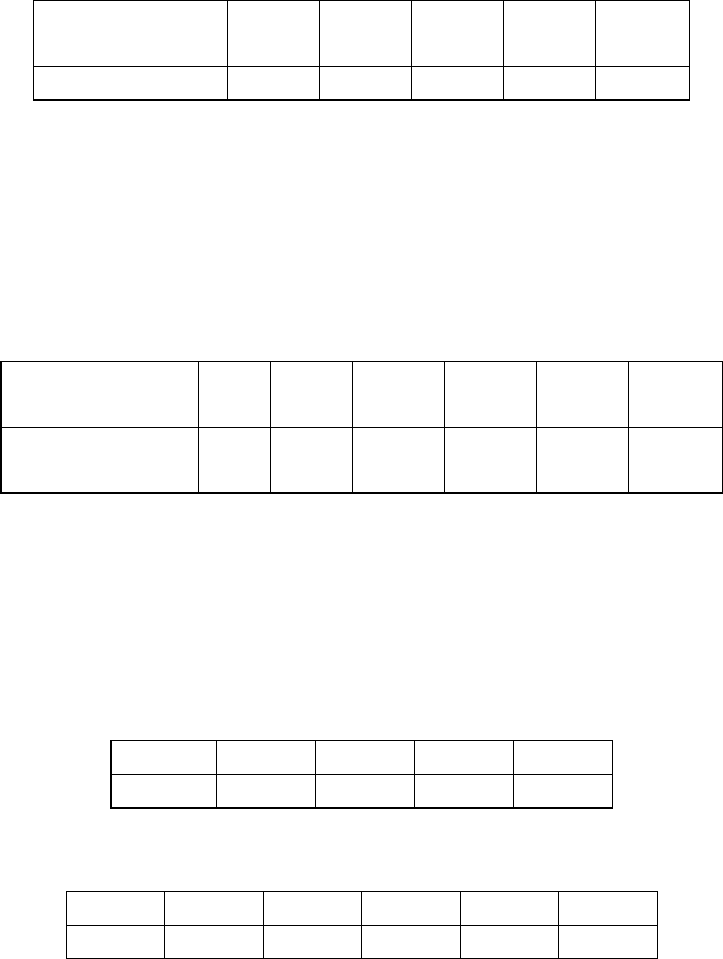
67. Дано распределение признака (случайной величины)

X – удой коров на

молочной ферме за лактационный период (в центнерах)

, полученного для

n = 100 коров.

4–6 6–8 8–10 10–12 12–14 14–16 16–18 18–20 20–22 22–24 24–26

1 3 6 11 15 20 14 12 10 6 2

Необходимо на уровне значимости 0,05 проверить гипотезу о нормальном

189

190

законе распределения признака (случайной величины) X, используя критерий

согласия χ

–Пирсона.

68. Было проверено 150 изделий с целью определения процента влажности

древесины, из которой они изготовлены. Получены следующие результаты:

Процент влаж-

ности

11-13 13-15 15-17 17-19 19-21

Число изделий 8 42 51 37 12

Необходимо на уровне значимости 0,05 проверить гипотезу о нормальном

законе распределения признака (случайной величины)

X, используя критерий

согласия χ

–Пирсона.

69. Распределение 200 элементов (устройств) по времени безотказной ра-

боты (в часах) представлено в таблице:

Время безот-

казной работы

0-5 5-10 10-15 15-20 20-25 25-30

Число уст-

ройств

133 45 15 4 2 1

Необходимо на уровне значимости 0,05 проверить гипотезу о показатель-

ном законе распределения признака (случайной величины)

X, используя крите-

рий согласия χ

–Пирсона.

70. Расход сырья на единицу продукции составил:

- по старой технологии

303 307 308 Всего

1 4 4 9

- по новой технологии

303 304 306 308 Всего

2 6 4 1 13

Полагая, что расходы сырья по каждой технологии имеют нормальные

распределения с одинаковыми дисперсиями, на уровне значимости 0,05 выяс-

нить, дает ли новая технология экономию в среднем расходе сырья.

Задача 8. Статистические методы обработки экспериментальных данных

71. На уровне значимости α = 0,1 проверить существенность влияния тем-

пературы на производительность установки (кг/ч).