Тырсин А.Н. Теория вероятностей и математическая статистика. Учебное пособие

Подождите немного. Документ загружается.

Составьте закон распределения, найдите математическое ожидание и диспер-

сию случайной величины: Z = (X – 1)2.

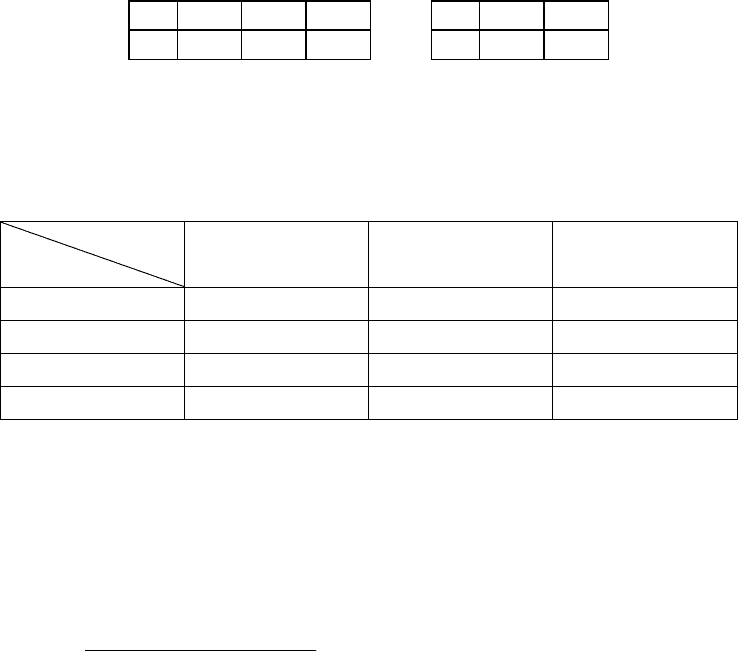
5.3. Даны законы распределения независимых случайных величин X и Y

X -1 0 1 Y 1 2

p 0,3 0,5 0,2 , p 0,4 0,6

Найти математическое ожидание и дисперсию случайной величины Z = X

5.4. Двумерная дискретная величина (X, Y) задана законом распределения:

2 3 4

2 0,3 0,15 0,05

3 0,15 0,10 0,05

4 0,05 0,05 0,05

5 0,05 0 0

Найти законы распределения составляющих X и Y, кковариацию и коэффициент

корреляции.

5.5. Двумерная случайная величина (X, Y) имеет плотность распределения веро-

ятностей

)25)(16(

),(

222

yxp

++π

Требуется: а) определить величину с; б) вычислить вероятность того, что X и Y

примут соответственно значения X< 4, Y< 5; в) найти функцию распределения

F(x, y)

6. Предельные законы теории вероятностей

6.1. Вероятность ошибки в каждом из ста счетов равна 0,2. Найти: а) вероят-

ность того, что ошибки имеются в 20 счетах; б) вероятность того, что число

счетов с ошибками заключено от двадцати до тридцати.

Указание: использовать локальную и интегральную теоремы Муавра–

Лапласа.

6.2. Вероятность выхода с автомата стандартной детали равна 0,96. Оценить ве-

роятность того, что число бракованных среди 2000 деталей находится в грани-

цах от 60 до 100.

Указание: использовать неравенство Чебышева.

171

172

6.3. Сколько следует проверить деталей, чтобы с вероятностью неменьшей 0,95

можно было утверждать, что абсолютная величина отклонения частоты годных

деталей от вероятности детали быть годной, равной 0,9 не превысит 0,01?

Указание: использовать теорему Бернулли.

6.4. При штамповке пластинок из пластмассы брак составляет 3%. Найти веро-

ятность того, что при проверке партии в 1000 пластинок выявится отклонение

от установленного процента брака меньше чем на 1%.

Указание: использовать теорему Бернулли.

6.5. Для определения средней урожайности поля площадью 1800 га взяли на

выборку по 1 м

с каждого гектара. Известно, что по каждому гектару поля

дисперсия не превышает 6. Оценить вероятность того, что отклонение средней

выборочной урожайности отличается от средней урожайности по всему полю

не более чем на 0,25 ц.

Указание: использовать теорему Чебышева.

6.6. Cколько следует провести независимых испытаний, чтобы вероятность вы-

полнения неравенства ⏐m/n – p⏐ ≤ 0,06 превысила 0,78, если вероятность появ-

ления данного события в отдельном испытании р = 0,7?

Указание: использовать теорему Бернулли.

6.7. Для определения средней продолжительности горения электролампы в пар-

тии из 200 одинаковых ящиков было взято на выборку по одной лампе из каж-

дого ящика. Оценить вероятность того, что средняя продолжительность горе-

ния отобранных 200 электроламп отличается от средней продолжительности

горения во всей партии по модулю меньше чем на 5ч, если известно, что сред-

нее квадратическое отклонение продолжительности горения ламп в каждом

ящике меньше 7ч.

Указание: D[X] < 49.

6.8. Производство дает 1% брака. Какова вероятность того, что из взятых на ис-

следование 1100 изделий выбракованных будет не более 17?

Указание: использовать интегральную теорему Муавра–Лапласа.

6.9. Вероятность изготовления детали первого сорта на данном станке равна

0,8. Найти вероятность того, что среди наугад взятых 100 деталей окажется 75

деталей первого сорта.

Указание: использовать локальную теорему Муавра–Лапласа.

7. Цепи Маркова

7.1. Вероятности перехода за один шаг в цепях Маркова задаются матрицей

⎥

⎦

⎤

⎢

⎣

⎡

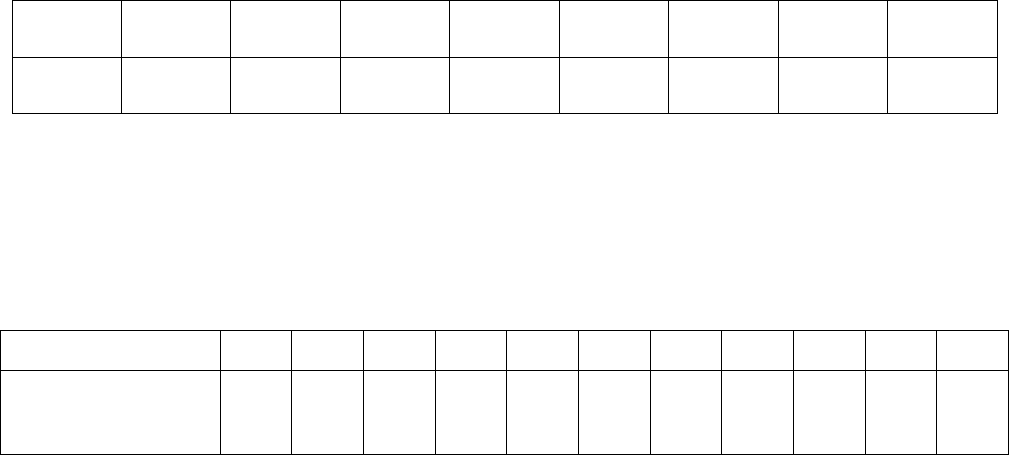
2/12/100

3/13/200

4/12/104/1

03/13/20

Требуется: а) найти число состояний; б) установить, сколько среди них сущест-

венных и несущественных; в) построить граф, соответствующий матрице P.

7.2. Матрица вероятностей перехода цепи Маркова имеет вид

⎥

⎦

⎤

⎢

⎣

⎡

3,01,06,0

3,02,05,0

5,03,02,0

P .

Распределение по состояниям в момент времени

t = 0 определяется вектором

. Найти распределения по состояниям в момент

t = 2.

)3,0;1,0;6,0(

8. Основные понятия выборочного метода

8.1. Результаты обследования роста рабочих приведены в таблице.

Рост,

см.

148−154 154−160 160−166 166−172 172−178 178−184 184−190 190−196

Число

рабочих

3 34 185 382 290 92 13 1

Требуется найти оценки математического ожидания, дисперсии и среднего

квадратического отклонения случайной величины

Х (роста рабочих).

8.2. Обзор счетов 400 инвесторов на фондовой бирже дал следующую инфор-

мацию о числе сделок в течение последнего квартала:

Число сделок, X 0 1 2 3 4 5 6 7 8 9 10

Число держателей

финансовых инст-

рументов

146 97 73 34 23 10 6 3 4 2 2

а) Найдите вероятность того, что случайно выбранный инвестор произвел ноль

сделок; по крайней мере, одну сделку; больше пяти; меньше шести.

б) Найдите математическое ожидание и дисперсию числа сделок.

в) Постройте график распределения.

8.3. Для имеющейся совокупности опытных данных (выборки) требуется: а) по-

строить интервальный статистический ряд и гистограмму распределения;

б) вычислить выборочную среднюю, выборочную дисперсию, выборочное

среднеквадратичное отклонение; в) выбрать теоретический закон распределе-

ния; г) построить теоретическую кривую распределения.

173

15,2 17,6 08,5 11,6 11,5 14,6 10,9 25,0 12,3 16,3

19,2 20,1 20,1 20,4 11,9 19,8 17,6 14,3 12,6 20,6

10,0 07,6 21,5 03,6 19,6 16,8 14,9 17,6 11,3 10,7

16,2 12,2 15,8 23,8 11,3 07,0 19,1 16,2 15,2 16

14,5 05,4 09,3 22,6 17,7 09,0 16,2 16,6 17,4 17,4

17,3 11,9 16,3 17,1 14,7 23,6 14,2 13,9 12,2 18,6

12,7 17,7 09,8 18,1 19,0 07,0 17,3 13,4 14,8 09,8

13,8 12,6 26,5 19,4 11,7 17,4 16,4 13,7 22,2 11,9

18,2 11,3 18,4 12,7 18,4 17,2 14,2 12,0 17,4 21,9

12,4 19,0 16,3 20,1 07,0 09,6 12,5 12,4 11,8 13,0

9. Точечное и интервальное оценивание параметров распределения

9.1. Найти доверительный интервал для оценки с надежностью 0,99 неизвестно-

го математического ожидания нормально распределенного признака

Х гене-

ральной совокупности, если даны генеральное среднее квадратическое откло-

нение σ

= 4, выборочная средняя

=10,2 и объем повторной выборки n = 16.

9.2. Имеется выборка объема

n = 13 из некоторой генеральной совокупности;

исследуемый количественный признак

этой совокупности распределен нор-

мально. По этой выборке найдены выборочная средняя

2,0=

и выборочная

дисперсия

= 0,48. Найти доверительный интервал, покрывающий параметр a

с надежностью 0,95.

9.3. По результатам 20 измерений получим

115

м., s

= 4м

. Найти точность

измерений с надежностью 0,95.

10. Проверка статистических гипотез

10.1. Дана выборка объёма

n = 100: 3,5 9 8,6 0,9 8,2 5,7 11 8,8 9,1 11 13 3,9 5 3,6

8,7 12 5,6 10 5 8,3 8,5 8,1 12 -1 12 0,6 1,6 3,4 8,8 2,5 3,8 7,9 8,5 12 4,9 2,9 0 6,2 5,5

4,2 12 1,1 16 2,5 11 8,7 8,6 4 4,6 8,4 6 5,8 7 7,6 13 6,9 3,3 6,2 12 6,8 8,6 5,2 5,1 6,6

10 4,9 3,6 14 3,2 8,8 1,4 4,1 8,3 1,9 6,7 3,6 8,5 3,3 3,5 7,5 4,9 -2 6,8 2,5 4,4 14 8,3

4,8 7,7 4,2 4,5 10 3,8 5,6 1,9 9,9 13 10 6,9 –3.

Требуется:

1) Сгруппировать выборку, округляя данные и объединяя малочисленные ин-

тервалы.

2) Построить гистограмму.

3) Найти выборочное среднее

и выборочную дисперсию

4) Используя критерий χ

–Пирсона при уровне значимости , проверить,

согласуются ли эти данные с законом нормального распределения.

05,0=α

5) На одном чертеже с гистограммой построить график теоретической плотно-

сти.

174

6) Если данные согласуются с законом нормального распределения, построить

доверительные интервалы для параметров

a и σ

, соответствующие довери-

тельной вероятности

9,01

α−=

175

7) Проверить гипотезу о стохастической независимости элементов выборки для

уровня значимости α

= 0,05 с помощью критериев «восходящих» и «нисходя-

щих» серий и Аббе.

10.2. Распределение 200 элементов (устройств) по времени безотказной работы

(в часах) представлено в таблице:

Время безотказной работы 0-5 5-10 10-15 15-20 20-25 25-30

Число устройств 133 45 15 4 2 1

Необходимо на уровне значимости 0,05 проверить гипотезу о показатель-

ном законе распределения признака (случайной величины)

X, используя крите-

рий согласия: а) χ

–Пирсона; б) Колмогорова–Смирнова.

10.3. Исследование в течение 10 дней производительности двух предприятий,

выпускающих холодильники, дало следующие результаты:

82 74 64 72 83 68 76 88 70 59

54 64 70 64 55 69 77 71 70 55

Проверить гипотезу об однородности двух выборок по критерию Вилкок-

сона–Манна–Уитни при уровне значимости α

= 0,1.

11. Основы дисперсионного анализа

11.1. На заводе установлено четыре линии по выпуску облицовочной плитки. С

каждой линии случайным образом в течение смены отобрано по 10 плиток и

сделаны замеры их толщины (мм). Отклонения от номинального размера при-

ведены в таблице:

Номер испытания Линия по выпуску

плиток

1 2 3 4 5 6 7 8 9 10

1 0,6 0,2 0,4 0,5 0,8 0,2 0,1 0,6 0,8 0,8

2 0,2 0,2 0,4 0,3 0,3 0,6 0,8 0,2 0,5 0,5

3 0,8 0,6 0,2 0,4 0,9 1,1 0,8 0,2 0,4 0,8

4 0,7 0,7 0,3 0,3 0,2 0,8 0,6 0,4 0,2 0,6

Требуется на уровне значимости α = 0,05 установить наличие зависимости

выпуска качественных плиток от линии выпуска (фактор

A).

11.2. На уровне значимости α

= 0,05 исследовать влияние цвета краски на срок

службы покрытия (мес.)

Номер опыта Синий Зеленый Красный

1 64 59 57

2 62 61 58

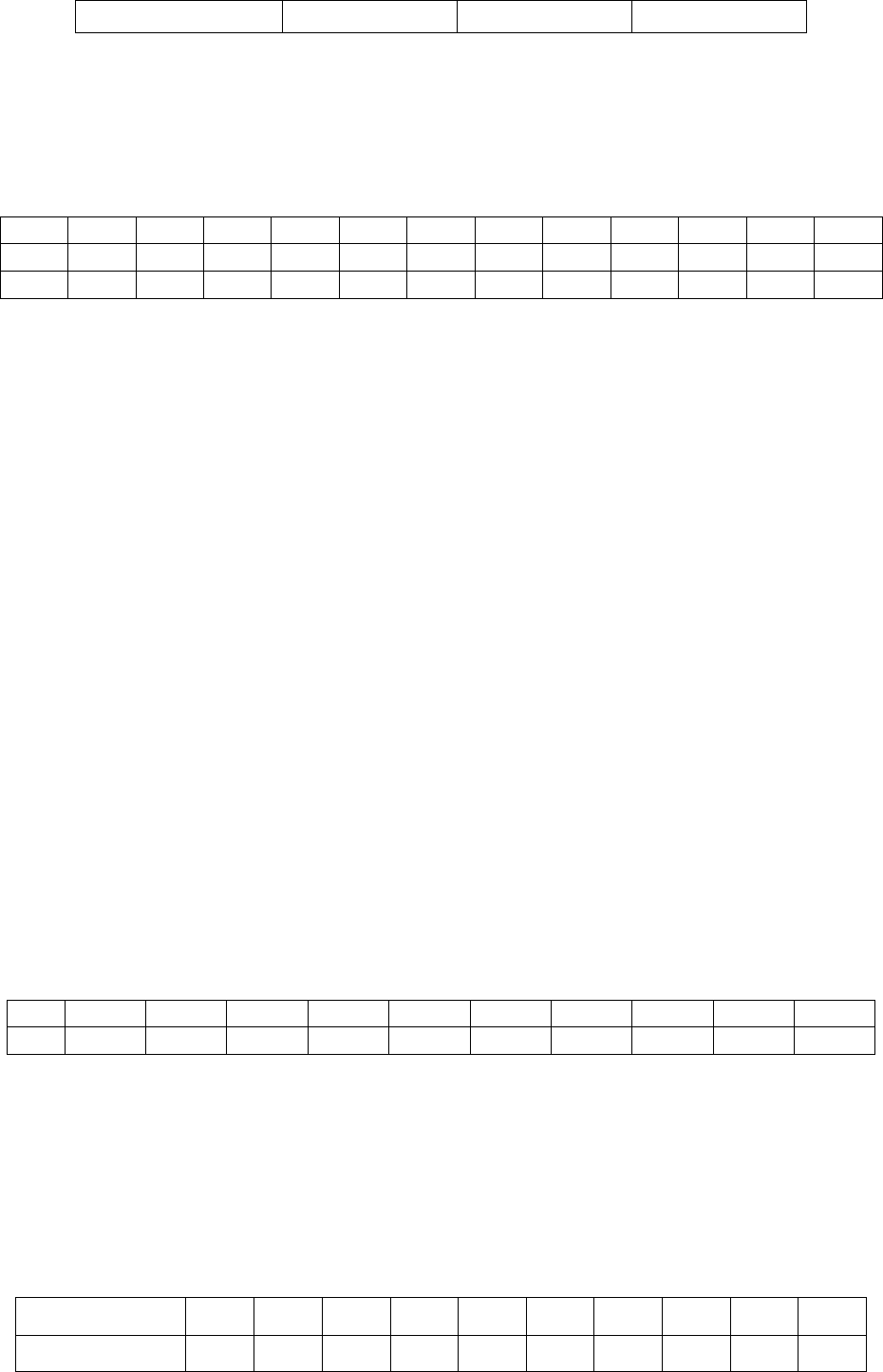
176

3 64 58 60

12. Корреляционный анализ

12.1. Имеются выборочные данные (в усл. ед.) по месячным доходам семей

сбережениями в банках

Y и ежемесячными расходами Z.

14,4 14,4 18,2 19,2 14,6 6,4 12,6 4,9 13,2 20,6 17,1 13,9

84 86 102 100 80 34 72 31 76 112 98 72

8,4 9,1 11,4 11,2 9,2 5,9 8,4 4,6 8,2 11,6 10,7 8,4

Выполните следующие задания:

установите по диаграмме рассеяния вид связи и тенденцию между всеми па-

рами признаков;

выберите адекватный измеритель статистической связи;

определите степень тесноты парных и частных связей;

проверьте гипотезы о значимости парных измерителей связи;

постройте интервальные оценки для парных коэффициентов корреляции;

вычислите парные ранговые коэффициенты корреляции Спирмена и Кен-

далла;

измерьте степень тесноты множественной связи;

проверьте гипотезу о значимости множественной ранговой связи между

всеми признаками;

по каждому заданию сделайте выводы в терминах решаемой задачи.

13. Элементы регрессионного анализа

12.1. По результатам десяти испытаний системы случайных величин (

X, Y) най-

ти выборочный коэффициент корреляции ρху и составить выборочное уравне-

ние линейной регрессии

Y на X. На координатной плоскости изобразить точка-

ми, полученные в результате испытаний пары значений случайных величин и

построить линию регрессии.

2,26 2,24 2,24 2,20 2,13 2,13 2,06 2,16 2,06 1,92

5,94 6,12 6,11 6,12 6,65 6,35 6,69 6,38 6,50 6,91

Проверить значимость полученного уравнения регрессии для α = 0,05.

12.2. Опрос случайно выбранных 10 студентов, проживающих в общежитии

университета, позволяет выявить зависимость между средним баллом по ре-

зультату предыдущей сессии и числом часов в неделю, затраченных студентом

на самостоятельную подготовку.

Средний балл 4,6 4,3 3,8 3,8 4,2 4,3 3,8 4,0 3,1 3,9

Число часов 25 22 9 15 15 30 20 30 10 17

Постройте график исходных данных и определите по нему характер зави-

симости. Рассчитайте выборочный коэффициент линейной корреляции Пирсо-

на, проверьте его значимость при

05,0

. Постройте уравнение регрессии.

Если студент занимается самостоятельно по 12 часов в неделю, то каков про-

гноз его успеваемости?

Ответы к задачам для самостоятельной работы

1.1. 1) Ω; 2)

А; 3) А; 4) А; 5) А; 6) ∅; 7) Ω; 8) ∅; 9) A.

1.3. 1) да; 2) нет; 3) да; 4) нет; 5) да; 6) да; 7) нет.

2.1. а)

; б)

2.2.

2.3. а)

; б)

; в)

2.4. 0,055.

2.5.

2.6. 0,9625.

2.7. 0,9984.

2.8. 0,96.

2.9. 0,975.

2.10. а) 0,58; б) 0,002.

2.11. а)

; б)

; в)

3.1. 0,12.

3.2. а) 0,21; б) 0,047; , в) 0,004.

3.3. 0,04565.

3.4. 0,0595.

3.5.

D[ξ] = npq.

3.6. а) 0,2048; б) 0,99968.

3.7.

0 1 2 3

= P(X = x

)

0,033 0,3 0,5 0,167

3.8.

6,1][ =X

;

34,1][ =X

;

158,1

3.9. а) 0,04979; б) 0,14936; в) 0,22404; г) 0,22404; д) 0,16803; е) 0,18474.

3.10.

6,0][ =X

;

46,0][ =X

. Распределение имеет вид:

0 1 2 3

177

= P(X = x

) 0,504 0,398 0,092 0,006

4.1.

][ =ξ

M ;

8][ =

4.2.

a = 1.

4.3. а) 0,1360; б) 0,6826.

4.4. 0,3.

4.5.

Р(|ξ – а| < 5 ) = 0,8664.

4.6. а) 4,01%; б) 0,135%.

4.7.

)1()1()(

eebXaP

λ−λ−

−−−=<<

5.1. ρ(

X, Y) = 0,688.

5.2.

M[Z] = 7,2; D[Z] = 32,16. Закон распределения имеет вид:

1 9 16

0,4 0,4 0,2

5.3. M[Z] = 2,6; D[Z] = 12,64.

5.5. а) 20; б)

6.1. а) 0,0997; б) 0,4938.

6.2. 0,808.

6.3. . 18000≥

6.4. 0,709.

6.5.

947,0>

6.6.

n > 265.

6.7.

Р > 0,99.

6.8.

1100

(0 ≤ k ≤ 17) = 0,9651.

6.9. Р

100

(75) = 0,04565.

7.1. а) 4 состояния; б) состояния

и E

, несущественны, поскольку остальные

состояния достижимы из них, но

недостижимо из E

, а E

недостижимо из E

;

состояния

и E

являются существенными.

7.2. В момент

t = 2: P(E

) = 0,437; P(E

) = 0,193; P(E

) = 0,37.

8.1.

53,170=

см.; см

702,38

;

221,6

см.

8.2. а) 635,0)0( ==X

, 635,0)0(

, 0425,0)5(

, 9575,0)6(

;

б)

M[X] = 1,535, D[X] = 3,379

9.1. )77,12;63,7(.

9.2. (

–0,24; 0,64).

9.3. . )00,356,1( <σ<

178

179

КОНТРОЛЬНАЯ РАБОТА

Общие указания

Необходимо строго придерживаться следующих правил:

1. Студент обязан делать контрольную работу №3 только своего варианта,

отсылая ее на рецензирование в сроки, предусмотренные графиком.

2. Контрольную работу следует выполнять в ученической тетради (отдель-

ной для каждой работы) чернилами любого цвета, кроме красного, оставляя по-

ля (3-4 см) для замечаний рецензента. Рекомендуется оставлять в конце тетради

несколько чистых страниц для исправлений и дополнений в соответствии с ука-

заниями рецензента.

3. На обложке тетради студент должен указать свою фамилию, имя, отче-

ство, также номер работы, ее название, номер зачетной книжки, номер вариан-

та, номера решаемых задач, форму обучения, специальность, курс, номер груп-

пы (образец оформления обложки приводится ниже).

Перед решением задачи нужно полностью выписать ее условие. Решение

каждой задачи студент должен сопровождать подробными объяснениями и

ссылками на соответствующие формулы, теоремы и правила. Вычисления

должны быть доведены до конечного числового результата. Ответы и выво-

ды, полученные при решении задач, следует подчеркнуть.

4. После получения отрецензированной работы студенту необходимо ис-

править все отмеченные ошибки и недочеты. Если работа возвращена на дора-

ботку, то следует переделать те задачи, на которые указывает рецензент.

Работы, выполненные без соблюдения этих правил, к зачету не при-

нимаются и возвращаются без рецензирования для переработки.

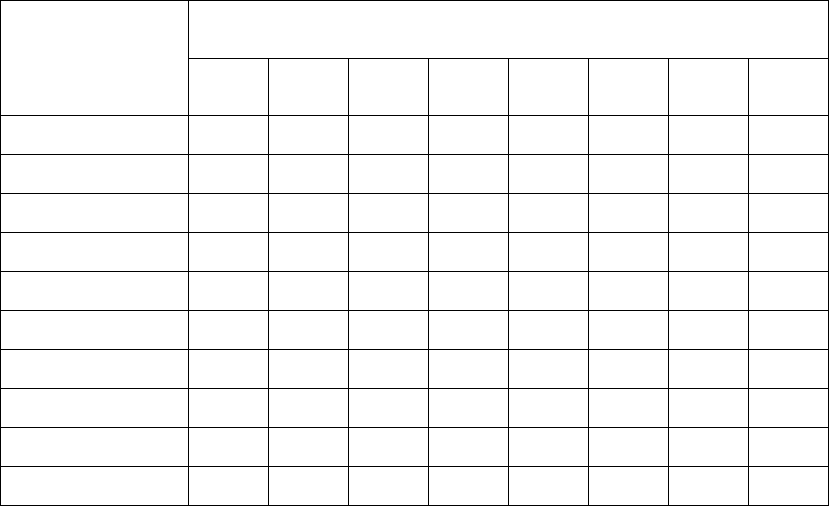
Контрольная работа содержит 8 задач. Номера задач выбираются из сле-

дующей таблицы

Задачи

Первая буква

фамилии сту-

дента

1 2 3 4 5 6 7 8

а, б 1 11 21 31 41 51 61 71

в, г 2 12 22 32 42 52 62 72

д, е 3 13 23 33 43 53 63 73

ж, з, и 4 14 24 34 44 54 64 74

к, л 5 15 25 35 45 55 65 75

м, н 6 16 26 36 46 56 66 76

о, п, р 7 17 27 37 47 57 67 77

с, т, у 8 18 28 38 48 58 68 78

ф, х, ч, ш, щ 9 19 29 39 49 59 69 79

э, ю, я 10 20 30 40 50 60 70 80

180

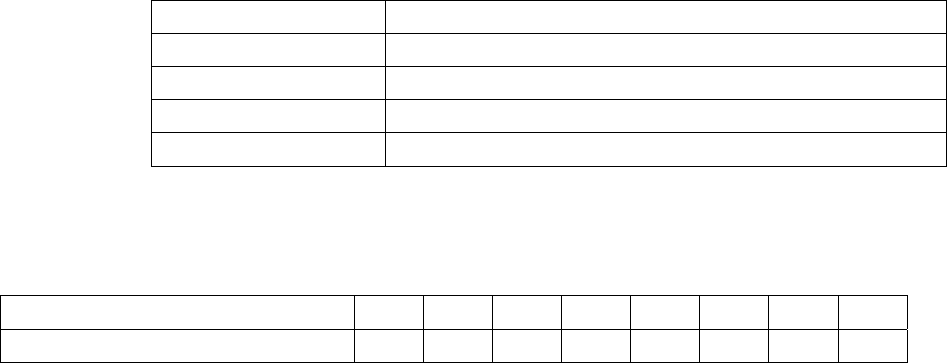
Образец оформления титульного листа

Челябинский государственный университет

Контрольная работа по математике

Семестр 3

Форма обучения:

Специальность:

Курс:

Группа:

Выполнил: Фамилия Имя Отчество

Номера задач по варианту:

Зачтено:

Челябинск – 2007