Тырсин А.Н. Теория вероятностей и математическая статистика. Учебное пособие
Подождите немного. Документ загружается.


Таблица 11.5
y
i
74 47 92 48 93 72 42 50 64 78 39 96 74 88 55 80 99 85
z
i
44 69 27 78 30 48 79 65 56 43 80 30 43 29 64 43 19 37
r
i
9,5 3 15 4 16 8 2 5 7 11 1 17 9,5 14 6 12 18 13
s
i
10 15 2 16 4,5 11 17 14 12 8 18 4,5 8 3 13 8 1 6
r
i
−
s
i
-0,5 -12 13 -12 11,5 -3 -15 -9 -5 3 -17 12,5 1,5 11 -7 4 17 7
(r
i
−
s
i
)
2
0,25 144 169 144 132,3 9 225 81 25 9 289 156,3 2,25 121 49 16 289 49
По формуле (11.15) 971,01910
1818
6
1
3
/
−=⋅
−
−=ρ
zy
. Однако при этом не
учтены связные ранги. По переменной Y имеем m
r
= 1 – одну группу неразли-
чимых рангов с t
r1
= 2 рангами. По переменной Z имеем m
s
= 2 – две группы не-
различимых рангов с t
s1
= 2 ранга и t
s2
= 3 ранга. Поэтому по формуле (11.17):
5,0)22(
12
1
3
=−=
r
T
,
5,2)]33()22[(
12
1
33
=−+−=
s
T
.
Отсюда находим по формуле (11.16)
977,0
)5,25,0(6/)1818(
1910
1
3
/
−=
+−−
−=ρ
zy
.
Для проверки значимости ρ
y/z
вычислим
327,18
977,01
218977,0
2
−=
−
−−
=
calc
t
. Далее
найдем . Поскольку
473,2)16(
025,0.
== tt
ucr
)16(
%5,2
tt
calc
>
, то коэффициент ρ
y/z
для данных переменных значим на 5%-ном уровне.
11.5.2. Коэффициент ранговой корреляции Кендалла
Коэффициент ранговой корреляции Кендалла между переменными X и Y
находится по формуле:
)1(
4
1
/
−
−=τ
nn
K
yx
, (11.19)
где K – статистика Кендалла, представляющая собой минимальное число обме-
нов между элементами последовательности s, необходимое для приведения ее к
упорядочиванию, аналогичному последовательности r.
Для определения статистики K необходимо ранжировать объекты по одной
переменной (пусть, для определенности по X) в порядке возрастания (при этом
ее ранги будут упорядочены (
n
rrr
≤
≤
≤
K
21
) и определить соответствующие
им ранги s
i
, (i = 1, … , n), переменной Y. Статистика K равна общему числу ин-
версий (нарушений порядка, когда большее число стоит слева от меньшего), в
ранговой последовательности s
1
, … , s
n
.
Формула (11.19) справедлива при отсутствии в ранжировках связных ран-
гов. Если они имеются, то коэффициент Кендалла определяют в виде:
⎥
⎦
⎤
⎢
⎣
⎡
−
−
⎥
⎦
⎤
⎢
⎣
⎡
−
−
−
+
−τ
=τ
∗
)1(
2
1
)1(
2
1
)1(
)(2
/
/
nn
V
nn
V
nn
VV
s
r
sr
yx
yx
, (11.20)
151
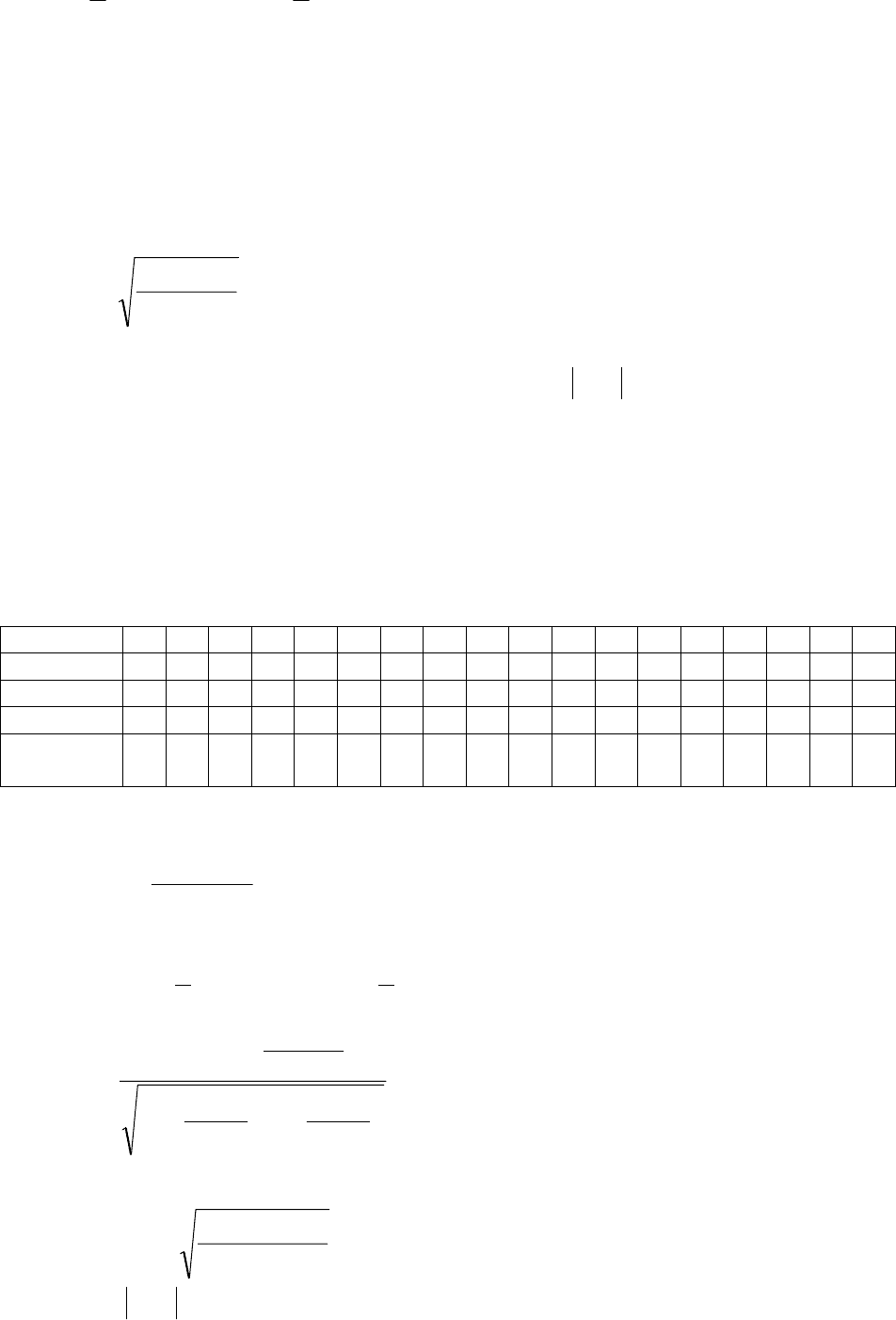
где
∑
=
−=
r
m
i
ririr
ttV
1
2
)(
2
1
,
∑
=
−=
s
m
i
sisis
ttV
1
2
)(
2
1
, (11.21)
m
y
, m
s
, t
ri
, t
si
− те же, что и при расчете коэффициента Спирмена.
Отметим, что в данном случае группы связных рангов не требуется при-
равнивать их средней арифметической по всей данной группе.
Свойства коэффициента Кендалла аналогичны свойствам коэффициента
Спирмена. При проверке значимости
τ
x/y
исходят из того, что в случае справед-
ливости гипотезы H
0
об отсутствии корреляционной связи между переменными
(при n > 10) критическая статистика
)52(2
)1(9
+
−
τ=
n
nn
u
cr
(11.22)
имеет стандартное нормальное распределение N(0, 1). Поэтому τ
x/y
значим на
доверительном уровне α, если расчетное значение
2/1 α−
> uu
calc
.
Пример 11.11. Для данных примера 11.2 определить с помощью коэффи-
циента Кендалла зависимость между стоимостью квартиры и ее удаленностью
от областного центра. Проверить значимость коэффициента с α = 0,05.
Решение. Составим таблицу, предварительно выполнив упорядочение всех
пар (y
i
,
z
i
) по возрастанию значений y
i
:
Таблица 11.6
y
i
39 42 47 48 50 55 64 72 74 74 78 80 85 88 92 93 96 99
z
i
80 79 69 78 65 64 56 48 44 43 43 43 37 29 27 30 30 19
r
i
1 2 3 4 5 6 7 8 9 9 11 12 13 14 15 16 17 18
s
i
18 17 15 16 14 13 12 11 10 7 7 7 6 3 2 4 4 1
Число ин-
версий
17 16 14 14 13 12 11 10 9 6 6 6 5 2 1 1 1 0
Сумма всех инверсий: K = 17 + 16 + … + 1 + 0 = 144. Теперь по (11.19)
882,0
)118(18
1444
1
/
−=
−
⋅
−=τ
zy
.
Поскольку имеются связные ранги, то определим из (11.21) поправочные коэф-
фициенты:
1)22(
2
1
2
=−=
r
V
,
4)]22()33[(
2
1
22
=−+−=
s
V
. Получим из (11.20)
930,0
1718
42
1
1718
12
1
1718
)41(2
882,0
/
−=
⎟
⎠
⎞
⎜
⎝
⎛
⋅
⋅
−
⎟
⎠
⎞
⎜
⎝
⎛
⋅
⋅
−
⋅
+
−−
=τ
∗
zy
.
Оценим значимость . Расчетное значение статистики согласно (11.22)
∗
τ
yx /
39,5
)5182(2
)118(189
93,0 −=
+⋅
−⋅
−=
calc
u
, 96,1
975,02/1
=
=
α−
uu .
Поскольку
975,0
uu
calc
>
, то коэффициент Кендалла значим на 5%-ном уровне.
152

Замечание 11.6. Вычисление коэффициента Кендалла более трудоемкое по
сравнению с коэффициентом Спирмена. Однако коэффициент τ
x/y
обладает не-
которыми преимуществами перед ρ
x/y
при исследовании его статистических
свойств и большим удобством его пересчета при добавлении к уже обследован-
ным объектам новых, т.е. при удлинении ранжировок.
11.5.3. Анализ множественных ранговых связей
В практике статистических исследований встречаются случаи, когда сово-
купность объектов характеризуется более чем двумя ранжировками и необхо-
димо установить статистическую связь между несколькими переменными. В
качестве такого измерителя используют коэффициент конкордации рангов
Кендалла W, определяемый по формуле
∑∑
==
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
+
−
=
n
i
m
j
j
i
x
nm
nnm
mW
1
2
1
)(
32
2
)1(
)(
12
)(
, (11.23)
где m − число анализируемых порядковых переменных; n − объем выборки;
− i-й ранг j-й порядковой переменной. Выражение (11.23) справедливо для слу-
чая отсутствия групп связных рангов. В противном случае используем формулу
)( j
i
x
∑
∑∑
=
==
∗
−−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
+
=
m
j
j
n
i
m
j
j
i
Tmnnm
x
nm
mW
1
32
1
2
1
)(
)(
12
1
2
)1(
)(
, (11.24)
где T
j
− поправочный коэффициент, определяемый по (11.17).
Коэффициент конкордации обладает следующими свойствами:
1) 0 ≤ W(m) ≤ 1;
2) W(m) = 1 при совпадении всех m анализируемых упорядочений;
3) Для случая m = 2 2/)1(),(
/
+
ρ
=
yx
yxW .
Проверка значимости коэффициента конкордации основана на том, что в
случае справедливости гипотезы об отсутствии корреляционной связи при n > 7
статистика имеет приближенно χ
Wnm )1( −=ψ
2
−распределение с (n − 1) сте-
пенями свободы. Поэтому коэффициент W значим на уровне α, если
)1()1(
2
%100
−χ>−
⋅α
nWnm
. (11.25)
Пример 11.12. Для данных примера 11.2 определить с помощью коэффи-
циента конкордации тесноту множественной статистической связи между
стоимостью квартир, их площадью и удаленностью от областного центра. Про-
верить значимость найденного коэффициента с α = 0,05.
Решение. Сформируем ранжировки для всех трех компонентов (m = 3) и
определим для всех i суммы . Результаты приведены в табл. 11.7.
∑
=
3
1
)(
j
j
i
x
153
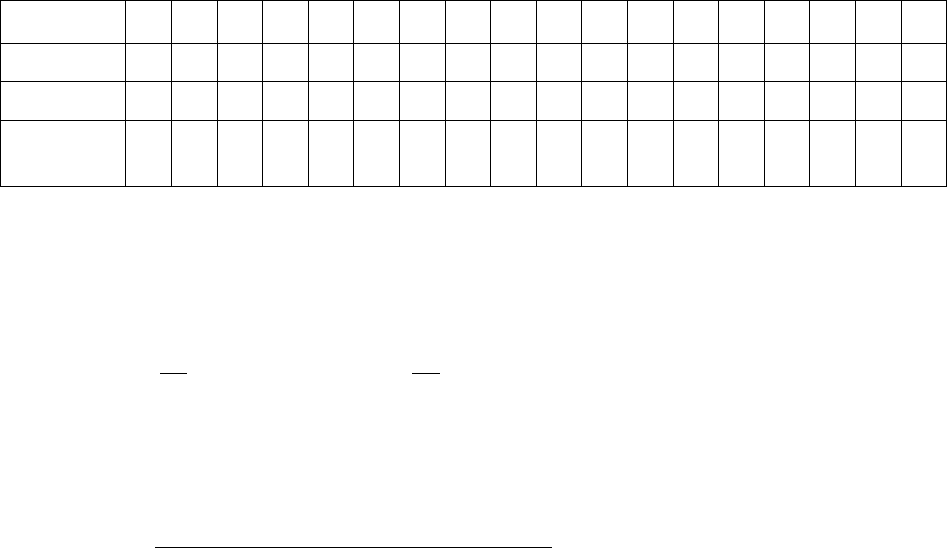
Таблица 11.7
)(Y
i
x
9 3 15 4 16 8 2 5 7 11 1 17 9 14 6 12 18 13
)(U
i
x
9 17 4 16 3 11 18 15 14 7 12 2 10 5 13 7 1 6
)( Z
i
x
10 15 2 16 4 11 17 14 12 7 18 4 7 3 13 7 1 6
∑
=
3
1
)(
j
j
i
x
28 35 21 36 23 30 37 34 33 25 31 23 26 22 32 26 20 25
В каждой ранжировке есть группы связных рангов: в и − по одной
группе из двух элементов, в − две группы из трех и двух элементов.
)(Y
i
x
)(U
i
x
)(Z
i
x
Вычислим поправочные коэффициенты:
5,0)22(
12
1
3
=−==
UY
TT
,
5,2)]33()22[(
12
1
33
=−+−=
Z
T
.
Далее, 5,282
/
1932
/
)1( =⋅
=
+nm . Числитель в (11.24) равен:
(28−28,5)
2
+ (35−28,5)
2
+ … + (20−28,5)
2
+ (25−28,5)
2
= 510,5.
Теперь подставляем в (11.24) полученные значения:
117,0
)5,25,05,0(312/)1818(3
5,510
)(
32
=
++−−
=
∗
mW .
Полученный результат свидетельствует об отсутствии одновременной тес-
ной зависимости между рассматриваемыми признаками.
Оценим значимость полученного значения W(m). Расчетное значение ста-
тистики:
967,5117,0173)1(
=
⋅
⋅
=−=ψ Wnm
calc
. Верхняя критическая точка:
. Неравенство (11.25) не выполняется, поэтому
одновременная статистическая связь между признаками не значимая.
587,27)17()1(
2
%5
2
%100
=χ=−χ
⋅α
n
Глава 12. Регрессионный анализ
Рассмотренный выше корреляционный анализ позволяет устанавливать
связь между случайными переменными и оценить ее тесноту. Регрессионный
анализ представляет собой следующий этап статистического анализа.
Задачами регрессионного анализа являются установление формы зависи-
мости между переменными, оценка функции регрессии и оценка неизвестных
значений (прогноз) зависимой переменной.
12.1. Основные положения регрессионного анализа
Определение 12.1. Регрессионный анализ – совокупность методов, позво-
ляющих исследовать вид односторонней зависимости объясняемой (зависимой)
переменной Y от одной или нескольких объясняющих (независимых) перемен-
ных
X = (X
1
, … , X
p
) и подбирать ее параметры.
Такие зависимости имеют вид модельного уравнения регрессии. Частным
случаем для одной объясняющей переменной является модель (11.1).
154

12.1.1. Задачи регрессионного анализа
В регрессионном анализе определяются точные количественные характе-
ристики изменения Y. Статистическая связь Y и
X сводится к строгим (неслу-
чайным) соотношениям. На данном этапе статистического анализа решаются
следующие основные задачи:
1) Выбор общего вида функции регрессии ;
),( Θϕ
∗
x
2) Отбор, если необходимо, наиболее информативных факторов;
3) Оценивание параметров уравнения регрессии
),,,(
21 l
θ
θ
θ
=
Θ
K
;
4) Анализ точности полученного уравнения регрессии путем построения дове-
рительных интервалов для коэффициентов регрессии, т.е. компонент вектора Θ,
для условного среднего отклика
)(x
y
и для прогнозов наблюдений отклика
при значениях факторов .
)(
∗
xy
),,(
1
∗∗∗
=
p
xx Kx
12.1.2. Многомерная нормальная регрессионная модель
Напомним, что при корреляционной связи между переменными, т.е. когда
условное математическое ожидание одной случайной переменной является
функцией значения, принимаемого другой случайной переменной,
)(][]/[ xYMxYM
x
ϕ
==
, где ϕ(x) − функция регрессии Y относительно X. В об-
щем случае функция регрессии ]
/
[)( xXx
=
=
ϕ
Y
M
описывает условное мате-
матическое ожидание от заданных значений факторов.
Практическое значение знания регрессионной зависимости заключается в
возможности прогнозирования значения зависимой случайной переменной Y,
когда независимая случайная переменная X принимает определенное значение.
Определение 12.2. Многомерная нормальная регрессионная модель описы-
вается уравнением
ε
+
ϕ= ),,(
1 p
XXY K , где функция регрессии ϕ(x) представ-
ляет закономерную часть одномерного отклика Y, ε − случайную часть отклика.
Определение 12.3. Регрессионную модель, удовлетворяющую основным пред-
посылкам 1
0
−5
0
называют гауссовской регрессионной моделью:
1
0
. Зависимая переменная Y есть величина случайная, а независимые перемен-
ные X
i
– неслучайные.
2
0
. Математическое ожидание остатка равно нулю, т.е.
0][ =ε
M
.
3
0
. Дисперсия остатка постоянна, т.е.
cons
t
D
=
ε
][
.
4
0
. Остатки ε
i
и ε
j
– не коррелированны, т.е. 0),cov(
=
ε
ε
ji
.
5
0
. Остатки ε
i
, i = 1, … , n распределены по нормальному закону.
Замечание 12.1. Для получения уравнения регрессии достаточно предпо-
сылок 1
0
−4
0
. Требование выполнения предпосылки 5 необходимо для оценки
точности уравнения регрессии и его параметров.
155
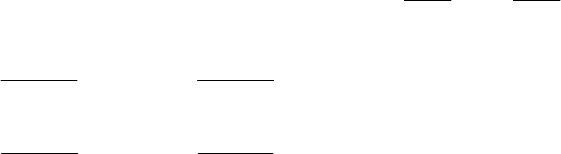
12.1.3. Выбор общего вида функции регрессии
Зависимость Y от X характеризуется формой и теснотой связи. Форма свя-
зи выявляет механизм получения зависимой случайной переменной Y. Она мо-
жет быть линейной ϕ(x) = β
0
+ β
1
x или нелинейной. Функция регрессии ищется
в одном из классов – параметрическом семействе. Среди нелинейных моделей
регрессии обычно рассматриваются следующие зависимости: квадратичная,
полиномиальная, экспоненциальная, мультипликативная, обратная по Y, гипер-
болическая и т.д. Вид зависимости выбирают исходя из визуальной оценки диа-
граммы рассеяния; опыта предыдущих исследований; знания сущности процес-
са. В ходе регрессионного анализа вид функции ϕ(x) может уточняться.
12.1.4. Оценивание параметров функции регрессии
Предложение 12.1. (Теорема Гаусса–Маркова). Если линейная регресси-
онная модель является гауссовской, то МНК−оценки ее параметров имеют наи-
меньшую дисперсию в классе всех линейных несмещенных оценок. #
Данное утверждение означает, что при введенных допущениях полученные
оценки обладают свойством эффективности. Если истинная модель регрессии
нелинейная или закон распределения величин
ε
i
неизвестен, то могут существо-
вать методы, дающие лучшие оценки параметров регрессии.
Параметры Θ оцениваются по исходным данным таким образом, чтобы ве-
личины )
,( Θϕ−=
)
iii
ye x , которые называются остатками, в совокупности бы-
ли близки к нулю. В МНК подбор параметров функции регрессии осуществля-
ется минимизацией суммы квадратов остатков:
[
444344421
)
ε
∑
=
Θ
Θϕ−=Θ
Q
n
i
ii
y
1
2
),(minarg x
]
. (12.1)
Найденная по (12.1) функция ),( Θϕ
)
x дает наименьшую среднюю квадра-
тическую погрешность прогноза величины Y по
X. Для нахождения оценок па-
раметров
01
b=θ
)
,
12
b=θ
)
, … , доставляющих минимум функции Q
ε
, приравни-
ваются к нулю все ее частные производные
K,0,0
10
=
∂
∂
=
∂
∂
εε
b
Q
b
Q
, откуда
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=
∂
ϕ∂
ϕ−
∂
ϕ∂
=
∂
ϕ∂
ϕ−
∂
ϕ∂
∑∑
∑∑
....
,0
)(
)(
)(
,0
)(
)(
)(
11
00
i
i
i
i
i
i
i
i
i
i
i
i
b
x
b
y
bb
y
x
x
x
x
x
(12.2)
Систему (12.2) называют системой нормальных уравнений.
Величина Q
ε
неотрицательна при любых b
0
, b
1
, … , и у нее должен сущест-
вовать хотя бы один минимум. Поэтому, если система нормальных уравнений
156

имеет единственное решение, то оно доставляет глобальный минимум для Q
ε
и
никаких дополнительных исследований на экстремум проводить не нужно.
12.2. Парная линейная регрессионная модель
Проиллюстрируем основные идеи регрессионного анализа на примере пар-
ной линейной модели.
12.2.1. Линейная одномерная модель регрессии
Функция регрессии ищем в виде
xbbxyx
10
)()(
+
=
=
ϕ
. Сумма квадратов
остатков равна . Система (12.2) принимает вид
∑
=
ε
−−=
n
i
ii
xbbyQ
1
2
10
)(
⎪
⎩
⎪
⎨
⎧
=+−
=+−
∑∑
∑∑
==
==
.0)(
,0)(
1
10
1
1
10
1
n
i
ii
n
i
ii
n
i
i
n
i
i
xxbbxy
xbby
После простых преобразований получим
⎪
⎩
⎪
⎨
⎧
=+
=+
∑∑∑
∑∑
===
==
.
,
11
2
1
1
0
11
10
n
i
ii
n
i
i
n
i
i
n
i
i
n
i
i
yxxbxb
yxbnb
(12.3)
Тогда коэффициент наклон егрессии и свободный член регрессии равны а р
(
)
(
)
()
2
11
2
111
1
∑∑
∑∑∑
==
===
−
⋅−
=
n
i
i
n
i
i
n
i
i
n
i
i
n
i
ii
xxn
yxyxn
b
,
n
xby
b
n
i
i
n
i
i
∑∑
==
−
=
1
1
1
0
. (12.4)
Для свободного члена равенство (12.4) можно переписать в виде
xbyx
n
by
n
b
n
i
i
n
i
i 1
1
1
1
0
11
−=−=
∑∑
==
, откуда
xbby
10
+
=
.
Это означает, что средняя точка
),(
y
x
совместного распределения величин X, Y
всегда лежит на линии регрессии ϕ(x). Поэтому при замене x на
x
x
−
получим
)()(
1
xxbyx
−
=−ϕ
. (12.5)
Отсюда следует, что для определения линии регрессии достаточно знать лишь
ее коэффициент наклона b
1
. Равенство для b
1
можно упростить, если использо-
вать найденное значение выборочного коэффициента корреляции r
xy
:
x
y
xy
s
s
rb =
1
, (12.6)
где s
y
и s
x
− оценки стандартных отклонений y
i
и x
i
вокруг своих средних
y
и
x
.
Из последнего выражения для b
1
видна роль коэффициента корреляции:
чем меньше r
xy
, тем ближе линия регрессии к горизонтальному положению, т.е.
тем ближе к состоянию неизменности будут средние значения наблюдений y
i
.
Пример 12.1. Для анализа зависимости объема потребления Y (у. е.) домо-
хозяйства от располагаемого дохода X (у. е.) отобрана выборка объема n = 12
(помесячно в течение года), результаты которой приведены в таблице 12.1.
Таблица 12.1
157
i
1 2 3 4 5 6 7 8 9 10 11 12
x
i
107 109 110 113 120 122 123 128 136 140 145 150
y
i
102 105 108 110 115 117 119 125 132 130 141 144
Необходимо определить вид зависимости и оценить по МНК параметры
уравнения регрессии.
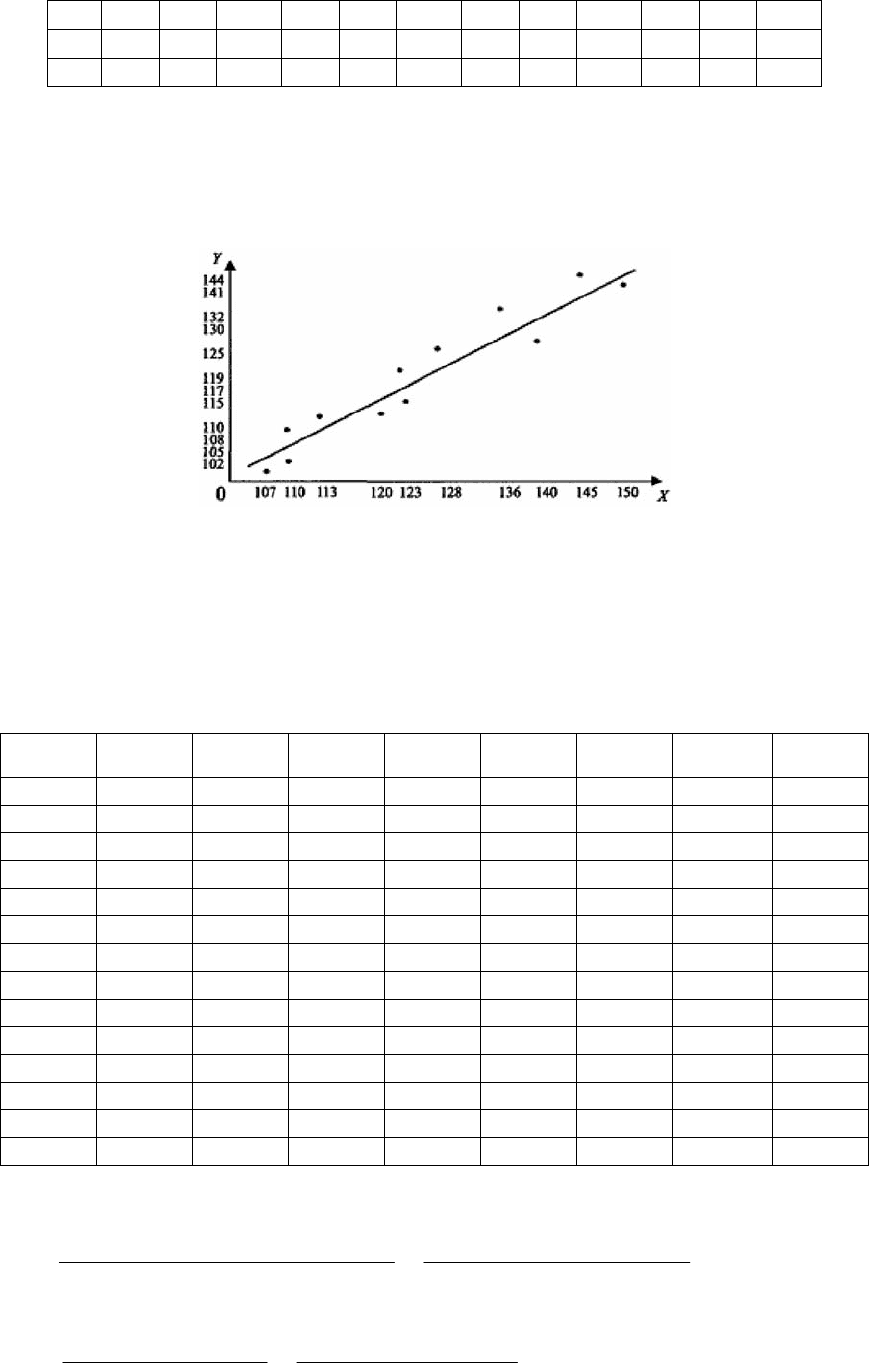
Решение. Построим диаграмму рассеяния (рис. 12.1).
Рис. 12.1. Диаграмма рассеяния.
По расположению точек на диаграмме рассеяния полагаем, что зависи-
мость между Y и X линейная:
xbbxy
10
)(
+
=
ϕ
=
)
.
Для наглядности вычислений по МНК построим таблицу 12.2.
Таблица 12.2
i x
i
y
i
2
i
x
x
i
y
i
2
i
y
i
y
)
e
i
2
i
e
1 107 102 11449 10914 10404 103,5832 -1,583 2,507
2 109 105 11881 11445 11025 105,4554 -0,455 0,207
3 110 108 12100 11880 11664 106,3914 1,609 2,587
4 113 110 12769 12430 12100 109,1997 0,800 0,641
5 120 115 14400 13800 13225 115,7522 -0,752 0,566
6 122 117 14884 14274 13689 117,6244 -0,624 0,390
7 123 119 15129 14637 14161 118,5605 0,440 0,193
8 128 125 16384 16000 15625 123,2409 1,759 3,094
9 136 132 18496 17952 17424 130,7295 1,270 1,614
10 140 130 19600 18200 16900 134,4739 -4,474 20,015
11 145 141 21025 20445 19881 139,1543 1,846 3,407
12 150 144 22500 21600 20736 143,8347 0,165 0,027
Сумма 1503 1448 190617 183577 176834 -
1,4⋅10
-14
35,249
Среднее 125,25 120,6667 15884,75 15298,08 14736,17 - - -
Согласно МНК имеем:
(
)
(
)
()
9361,0
150319061712
1448150318357712
22
12
1
12
1
2
12
1
12
1
12
1
1
=
−⋅
⋅−⋅
=
−
⋅−
=
∑∑
∑∑∑
==
===
i
i
i
i
i
i
i
i
i
ii
xxn
yxyxn
b
,
423,3
12
15039361,01448
12
1
1
12
1
0
=
⋅−
=
−
=
∑∑
==
n
xby
b
i
i
i
i
.
Таким образом, имеем уравнение парной регрессии
x
y
9361,0423,3 +
=
)
.
158
12.2.2. Оценка точности регрессионной модели
Построим доверительные интервалы для коэффициентов регрессии и зави-
симой переменной Y.
Интервальные оценки коэффициентов регрессии.
Доверительные интервалы позволяют проверить значимое отличие коэф-
фициентов от нуля. Пусть β
0
, β
1
− коэффициенты истинной регрессии. Важной
является гипотеза H
0
о коэффициенте наклона, H
0
: β
1
= 0. В этом случае пере-
менная Y изменяется чисто случайно, не завися от значений X. Гипотезу H
0
сле-
дует отвергнуть против двусторонних альтернатив β
1
≠ 0 на уровне значимости
α, если число 0 не входит в доверительный интервал для β
1
.
Построение доверительных интервалов для параметров β
0
, β
1
основано на
том, что отношения и
0
/)(
00 b
sb β−
1
/)(
11 b
sb
β
−
имеют распределение Стьюден-
та с (n−2) степенями свободы, где b
0
, b
1
− оценки коэффициентов регрессии,
полученные при решении системы (12.4), , − оценки стандартных откло-
нений коэффициентов регрессии. Тогда доверительные интервалы для пара-
метров β
0
b
s
1
b
s
0
, β
1
при надежности оценки (1−α) равны:
0
)2(
2/0 b
sntb ⋅−±
α
и
1
)2(
2/1 b
sntb
⋅
−
±
α
, (12.7)
Для , выполняются свойства:
0
b
s
1
b
s
∑
=
ε
−
=
n
i
i
b
xx
s
s
1
2
)(
1
,
10
2
1
2
1
2
)(
b
n
i
i
n
i
i
b
sx
xxn
xs
s =
−
=
∑
∑
=
=
ε
.
Число связей (коэффициентов) для линейной модели l = 2, поэтому
∑
=
ε
−−
−
=
n
i
ii
xbby
n
s
1
2
10
2
)(
2
1
. (12.8)
Из (12.7) можно получить условия для проверки значимости (в смысле отличия
от нуля) оценок коэффициентов регрессии. Действительно, учитывая, что при
выполнении гипотезы H
0
теоретические коэффициенты регрессии β
0
= β
1
= 0,
получим соотношения для критических статистик
0
0
0
b
b
s
b
t =
,
1
1
1
b
b
s
b
t =
.
Эти статистики при справедливости H
0
имеют распределение Стьюдента с
числом степеней свободы (n–2). Отсюда условиями, при которых оценки b
0
, b
1
будут значимыми с надежностью (1−α), являются:
)2(
%1002/
0
−≥
⋅α
ntt
b
,
)2(
%1002/
1
−≥
⋅α
ntt
b
.
Доверительные области для зависимой переменной.
Одной из центральных задач регрессионного анализа является прогнозиро-
вание значений зависимой переменной при определенных значениях объяс-
няющих переменных. Здесь возможны два варианта:
1. Предсказать условное математическое ожидание зависимой переменной
при определенных значениях объясняющих переменных (предсказание средне-
го значения).
159
2. Предсказать некоторое конкретное значение зависимой переменной
(предсказание конкретного значения).
Построим вначале доверительную область для условного математического
ожидания зависимой переменной (для модели регрессии M[Y/X = x
p
]. Пусть по-
строено уравнение регрессии
ii
xbbxy
10
)(
+
=
на основе которого нужно пред-
сказать условное математическое ожидание M[Y/X = x
p
] = β
0
+ β
1
x
p
переменной
Y при X = x
p
. Возникает вопрос: как сильно может уклониться значение )(
p
xy
от M[Y/X = x
p
]. Можно показать, что статистика
)(
][)(
p
xy
xp
s
YMxy
T
−
=
, где
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
−
+=
∑
=
ε
n
i
i
p
xy
xx
xx
n
ss
p
1
2
2
22
)(
)(
)(
1
,
2
1
2
2
−
=
∑
=
ε
n
e
s
n
i
i
, имеет t−распределение Стьюдента с
(n−2) степенями свободы, и построить доверительную область для условного
математического ожидания M[Y/X = x
p
]:
)(2/1010)(2/10
)2()2(
pp
xyppxyp
sntxbbxsntxbb ⋅−
+
+
<
β
+
β
<
⋅−−+
αα
.
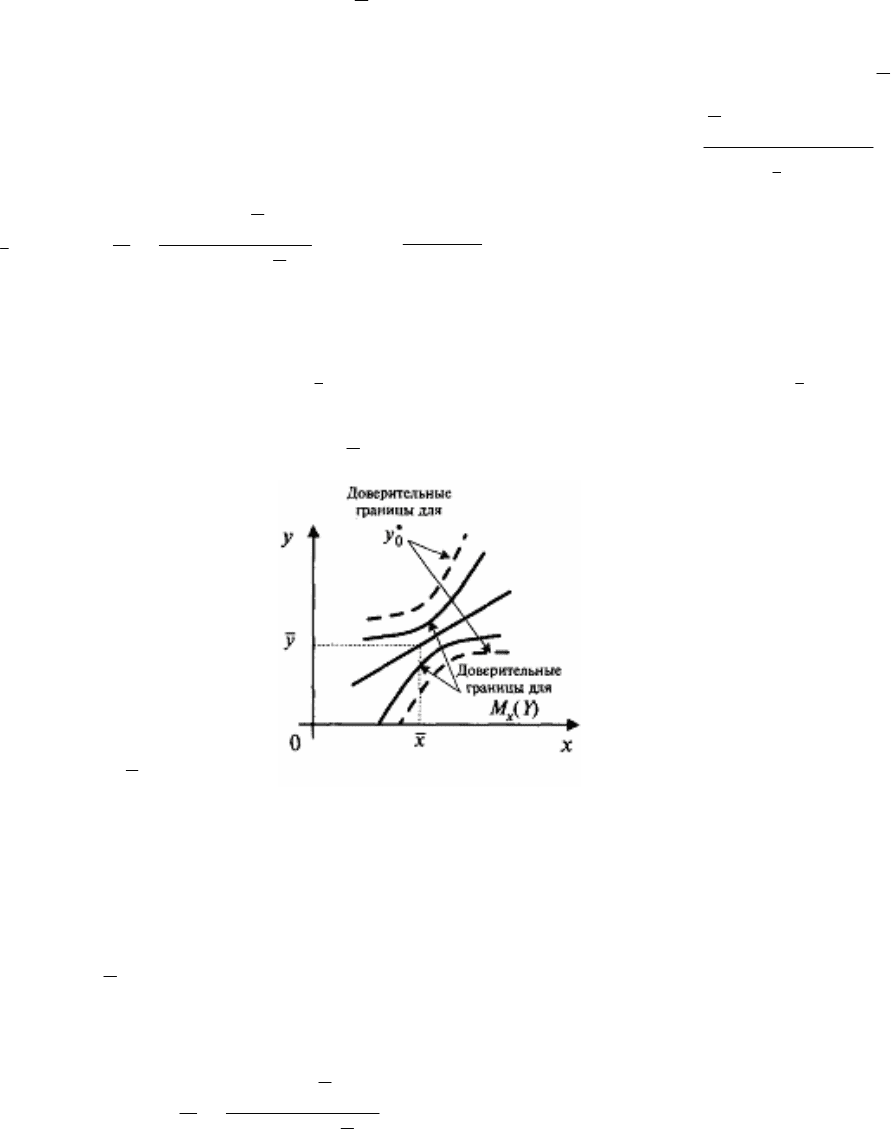
(12.9)Величина доверительной области (12.10) зависит от значения объясняю-
щей переменной x
p
: при xx
p
= она минимальна, и увеличивается по мере уда-
ления x
p
от
x
(рис. 12.2).
Рис. 12.2.
Построенная доверительная область для M
x
[Y] определяет местоположение
модельной линии регрессии (условного математического ожидания), а не от-
дельных возможных значений зависимой переменной, которые отклоняются от
среднего
x
. Получим теперь доверительную область для индивидуальных зна-
чений зависимой переменной.
Оценка дисперсии индивидуальных значений y
p
при x = x
p
равна
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
−
++=
∑
=
ε
n
i
i
p
y
xx
xx
n
ss
p
1
2
2
22
)(
)(
1
1
,
а доверительная область для прогнозов индивидуальных значений y
p
определя-
ется по формуле
pp
yppyp
sntxbbysntxbb
⋅
−
+
+
<
<
⋅−−+
αα
)2()2(
2/102/10
. (12.10)
160
