Тынянский Н.Т., Жуковский В.И. Дифференциальные игры с ненулевой суммой (кооперативный вариант)

Подождите немного. Документ загружается.

ситуации. Именно, в игре, представленной на рис. 2, равновес-

ный по Нэшу набор 0,1 одновременно является и оптимальным

ло Парето. Теперь составим таблицу выигрышей для всех воз-

Игрок 2

0,-5

—9,

—9

-4,-4

—5,

Рис.

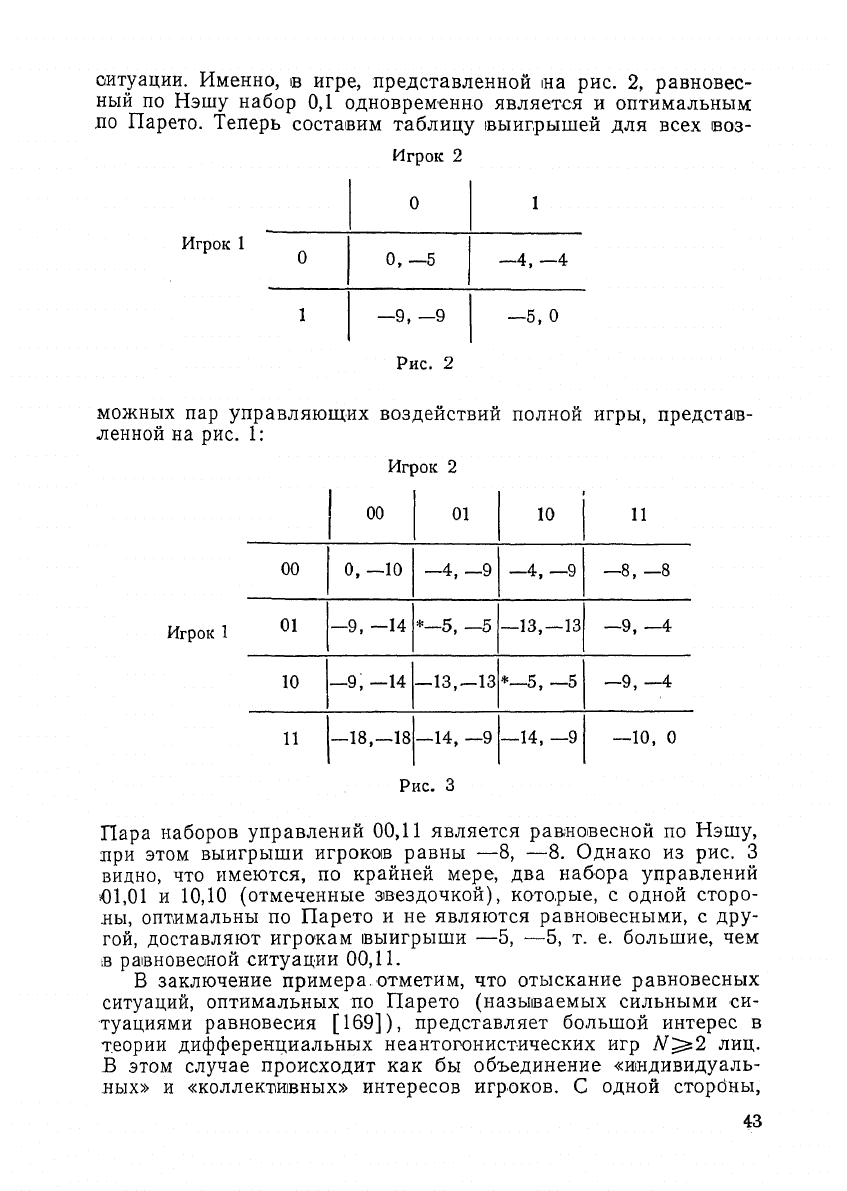
можных пар управляющих воздействий полной игры, представ-

ленной на рис. 1:

Игрок 2

0,—10

—9,

-14

—9,

-14

-18.—18

-4,-9

*__5,

—5

—13.—13

—14,

—9

—4,—9

—13,-13

*_5,

-5

-14,

-9

-8,-8

—9.—4

—9,-4

—10,

Рис.

Пара наборов управлений 00,11 является равновесной по Нэшу,

при этом выигрыши игроков равны —8, —8. Однако из рис. 3

видно, что имеются, по крайней мере, два набора управлений

О1,01 и 10,10 (отмеченные звездочкой), которые, с одной сторо-

ны,

оптимальны по Парето и не являются равновесными, с дру-

гой,

доставляют игрокам выигрыши —5, —5, т. е. большие, чем

в равновесной ситуации

00,11.

В заключение примера, отметим, что отыскание равновесных

ситуаций, оптимальных по Парето (называемых сильными си-

туациями равновесия [169]), представляет большой интерес в

теории дифференциальных неантогонистических игр N^2 лиц.

В этом случае происходит как бы объединение «индивидуаль-

ных» и «коллективных» интересов игроков. С одной сторбны,

каждому игроку не имеет смысла отклоняться, от решения игры

(в силу определения равновесности по Нэшу), с другой, не-

сколько игроков (два или более), не придерживаясь решения

и увеличивая свой -выигрыш, обязательно вызовут «ухудшение»

выигрыша одного из оставшихся. Этот вопрос связан с «улуч-

шаемостью»

[151],

точнее, с «неулучшаемостью» равновесных

ситуаций и в литературе почти не рассматривался. Некоторые

подходы, скорее на «эвристическом» уровне, анонсированы в

[347].

Для стохастических дифференциальных игр с ненулевой

суммой достаточные условия того, что равновесный набор пози-

ционных управлений совпадает с оптимальным по Парето, по-

лучены Варайа [351] (см. § 12, п. 12.3). Заметим, что в эконо-

мических задачах довольно часто встречаются равновесные

ситуации, оптимальные по Парето

[201].

Как показано в приведенном примере, принцип оптимально-

сти,

как необходимое условие существования решений, не всег-

да верен. Естественно задаться ©опросом об отношении прин-

ципа оптимальности к достаточным условиям. Этот вопрос

является принципиальным при использовании метода динамиче-

ского программирования в задачах неантагонистических диф-

ференциальных игр. Именно, в .основу метода динамического

программирования и должен быть положен принцип оптималь-

ности в форме достаточного условия. Однако в теории неанта-

гонистических дифференциальных игр возникла такая же

ситуация, как и в теории оптимального управления (подробно

об*

этом в [26]): принцип оптимальности при решении конкрет-

ных задач лишь декларируется, не по существу не использует-

ся

[322].

При выводе соответствующих уравнений Беллмана

не буквально выписываются соотношения, следующие из прин-

ципа оптимальности, а осуществляются преобразования, хотя

и ведущие к уравнениям Беллмана, но законность преобразова-

ний следует из других {как правило, простых) математических

фактов. То есть,

;

фактически, принцип оптимальности исполь-

зуется в теории неантагонистических дифференциальных игр

как наводящее соображение при выводе уравнений Беллмана..

§ 2. Среднеквадратичное решение

В п. 2.1 описываются свойства среднеквадратичного реше-

ния, в частности, доказано, что это решение является одновре-

менно оптимальным по Парето. Необходимым и достаточным

условиям посвящен п. 2.2.

2.1.

Определение и свойства. М. Е. Салуквадзе в серии

статей 1971 г. [1361 предложил подход к решению задачи опти-

мального управления с векторным критерием. В основу положено*

определение идеальной (утопической) точки /* = {/*, i =

...

.'.. .,N\I*= max

(и[•

J)}

в пространстве критериев $*

1/2

и введение нормы /гС^Н)-

j2l-

—

Л(

Н)]

[

этом про-

странстве. Этот подход развит в [143, 332, 333] и подробно изло-

жен М. Е. Салуквадзе в монографии

[135],

где решено и боль-

шое количество практических задач. Идея «приближения к иде-

альной точке»

—

основа метода целевого программирования Чар-

каса и Купера [204,205]. Ими рассмотрены разные метрики,

в том числе и используемая здесь евклидова.

Перейдем к изложению основных результатов.

Среднеквадратичным решением для игры (10)

—

(11) называет-

ся набор управляющих воздействий и? \t\ та-сой, что

(«

Н)== mm /

(«[-I)=- min ||/*-/(«[•]) ||

Среднеквадратичное решение обеспечивает максимальную

близость выигрышей игроков 1л(и

[-]) к их максимальным

выигрышам /<*,

t—1,...,

/V, (минимальная групповая неудов-

летворенность) и ряд других игровых свойств (Ю [365]).

Из леммы 8 следует, что среднеквадратичное решение опти-

мально по Парето для игры

(10)

—(11) здесь

= 2 К*

-7

*-!

Такой подход для случая статических систем был развит

Ю [360

—365],

Фромером и Ю

[232].

В указанных работах опти-

мальные по Парето решения выделены путем минимизации более

общей нормы, чем квадратичная. Именно, /^-решением и'гры

(10) —(11) называется набор управляющих воздействий uP\t\,

такой, что

(иР\-\)

minL/,(«!-])•

«l-16^

где

i/p

ПрИ

< "•< со ,

(u)

= \U-i

max '(/i —/-(и)) при р= со.

}•= 1

Так как разность /**—/•*(") составляет потерю выигрыша 1-го

игрока, то u

[t] минимизирует сумму индивидуальных потерь,

Щ минимизирует максимальную индивидуальную потерю, а

uP[t], \<p<oo, минимизирует групповую потерю «групповое

сожаление»

[368],

Укажем ряд полезных свойств р-решения

[232].

Обозначим

I{°U) множество выигрышей игроков, когда набор управляю-

щих воздействий пробегает все возможные значения.

а) Если I\°U) выпукло, то существует единственный набор

выигрышей

{h(ИР[•]),...,

я("

[-])} при 1<р<оо, если

же I{°U) строго выпукло, то единственность сохраняется и при

б) Если 1{°и) выпукло и компактно в R

, то /-

является

непрерывной функцией р при 1</?<оо.

в) При N—2 имеют место следующие свойства монотонно-

сти:

ири l{le}^<p<co.

2 2

2Л(^[-1)<2Л(^1-1) и max{/I—/i(^H)}<

i=l

i=! -=--2

max

{/J-/•

(а'Н)}-

i=l,2

Отметим, что И. А. Корниенко

[80] приведена минимакс-

ная постановка среднеквадратичной задачи и показана ее связь

с задачей векторного минимакса (п. 7.3 из § 7).

2.2.

Необходимые и достаточные условия. Предположим,

что в (10)-(11) функция / явно не зависит от времени, не-

прерывно дифференцируема;

и &i(x), i = l,

...,N,

не-

прерывно дифференцируемы; набор программных управлений

u(t) таков, что ||к(01|<Const = р>0 и компоненты u{t)

кусочно-непрерывны и порождает x(t)

—

единственное реше-

ние (10), определенное при всех t£\t

,T], и такое, что x(t

) =

;

задано начальное значение фазового вектора х

, но

моменты ^-начала, Г-окончания игры и значение х(Г)

не фиксированы. Пусть найдены Ф*= max Ф

(х(Г)). Введем

функционал

Ф {х (Г))

= 2 [

* ~

®i

(

))Г-

г-=1

Отыскание среднеквадратичного решения сводится к реше-

нию следующей задачи оптимального управления: найти набор

программных управлений u

(t), реализирующий минимум

Ф(х(Т)) при ограничениях

x=f{x,u),

x(t

) =

Применение принципа максимума Л. С. Понтрягина [126] при-

водит к следующим необходимым условиям

[135]:

если и

{t)-~

среднеквадратичное решение, то существует непрерывная функ-

ция ty(t) =

{tyi{t),

. ..,^„(-9} такая, что

Н (х

(t),

-ф

(*))

= max Я (х

(t), и,

i|>

(t)),

II»IKP

где Н(х, и,

ty)

= ty'f(x, u), a ty(t)—решение системы

•г df(x

(t) u

(t))

-ф =

_-|/_———i-iz——У--,

кроме того, выполнено условие транс-

версальности

^дФ^л^

Ьх

(г)

я {хс

цс

{i)

{t))bt+

{T)bx{T)

Отсюда при свободном конце Т получаем равенства

H(x°{T),u<(T),q(T)) = 0, у(Т)=-

дФ(х

(Т)

первое из которых определяет время Т окончания игры.

М. Е. Салуквадзе доказан £135] следующий результат:

если для каждой задачи

Ф]

= тахФ

(х (Т)) выполняются необ-

ходимые условия оптимальности (принцип максимума), то имеют

место и приведенные необходимые условия.

Достаточные условия сводятся к следующим требованиям:

а) существует абсолютный минимум функции

(—7)~)

)*-

который достигается при и = и

(х, -г-), здесь |]и||<р; б) суще-

ствует гладкое решение V

(х) уравнения (—— \ f ix

(х,

-——jj

= 0 с граничйым условием V (х (Т)) = Ф(х(Т)); тогда

/ dv°\

ix,

--—1 —

среднеквадратичное решение.

Заметим, что, используя приведенные условия, М. Е. Салук-

вадзе [135] нашел решение некоторых вариантов следующих

практических задач, в которых учитывались несколько целевых.

функционалов: полет на заданной высоте, полет беспилотного

самолета, оптимальный взлет в заданную точку пространства..

вертикальный взлет ракеты в 'пустоте и задачу аналитического

конструирования регуляторов при векторных показателях ка-

чества. Е. П. Маслов и В. Н. Харчев [93] провели сравнение

выигрышей игроков при среднеквадратичном решении с мини-

максным в задаче преследования, а Л. И. Кожинская и

Л.

И. Слуцкий [77] —с арбитражным решением (§ 3) (при

анализе работы системы «оператор — манипулятор»).

§ 3. Решение Нэша для арбитражной схемы

В п. 3.1 доказано, что решение Нэша является одновременно'

оптимальным по Парето. Необходимые и достаточные условия

отнесены соответственно в п. 3.2 и 3.3. В п. 3.5 рассмотрен

подход к классической задаче о сделке, основанный на страте-

гиях угроз, конечно, применительно к дифференциальной игре.

3.1.

Определение. Арбитражная схема есть функция, которая

связывает с каждой игрой единственный выигрыш игрокам

[89].

Набор управляющих воздействий, реализующий эти

выигрыши, называется арбитражным или компромиссным ре-

шением. В теории статических (не дифференциальных) игр

используется несколько арбитражных схем. В дифференциаль-

ных играх пока нашла применение лишь арбитражная схема

Нэша, предложенная им для классической задачи торга

[307].

Пусть /J (^

)

max mm

/i(^i[-],

«.vvl.]).

£==1-...,

, —ra-

«•I-l

N\iH

•рантированный выигрыш г-го игрока в игре

(10) —

(11).

Арбитраж-

ная схема состоит в максимизации произведения «приращений

выигрышей» всех игроков. Именно, набор управляющих воздей-

ствий u

\t\ называется решением Нэша для игры (10)

—(11),

если

ту

(и

\-])= тах7

(а[-])--= шах IIU*

("I'1)

—•-'?}

при дополнительных ограничениях /i(«

[-])>/5, i

—

l,...,

Далее, в этом параграфе для сокращения записи будем пред-

полагать, что в игре участвует только два игрока (N =

2),

тогда

/-*(«)•=

[/, (и)—/;н/

(а)-/21.

Решение Нэша удовлетворяет некоторой системе аксиом. Сам

вид арбитражной схемы (функции

(и))

определяется этой

системой аксиом также единственным образом [89].

Докажем, что решение Нэша u

[t] для игры (10)

—

(11)

оптимально по Парето. Предположим противное, тогда сущест-

вует набор u*[t] такой, что система неравенств, из которых по

крайней мере одно строгое, /<(«*[• ])^/*(и

[-]) (i—l, 2) со-

вместна. Поэтому совместна и система /.•*(#*[•])—Л

^li(u

[-])—h

(i—1, 2). Но, согласно ограничению, ц(и

[-])>

поэтому ?

(«*[•])>/

(гг

[.]), что противоречит определе-

нию решения Нэша.

Заметим, что, кроме оптимальности по Парето, решение

Нэша обладает и рядом других специфических игровых свойств

189].

3.2.

Необходимые условия. Предположим, что система (10)

-автономна:

x = f(x, щ, щ), хеХс%\ u&UiCzR^ (i = l, 2); (33)

определено терминальное множество

МадХ,

а каждый набор

позиционных управлений u(x) = {ui{x), и

(х)} порождает един-

ственное решение x(t), ^

<jf<7\ системы (33) такое, что

x(t

) = x

, x(t)GX\M при *6l*o» T) и

х(Т)еМ.

Выигрыш i-того игрока (11) определяется

It(x

, a[-\, M)=^F

(x(f), a(x(t)))dt

= \, 2). (34)

Необходимые условия существования решения Нэша для

игры (33)— (34) в классе позиционных управлений получены

Ори 1.249]: предположим, что найдены

= Vi(Jc

)

—

7J и, для

любых х$Х, —функции V

(x) = I

(x,

[-\,

М)

= l,2). Если

функции Vi\x) непрерывно дифференцируемы, а и

(х)

—

реше-

ние Нэша для игры

(33) —(34)

(соответствующую траекторию (33)

обозначим

{t),

<2?<.Г), то при почти всех /б

[--о»

-П

всех

•#i{in}£/i

(г

=—

2) выполняется неравенство:

hifax'V)'

(x^(t))) + (

if))

)'f(x^t)

и»

(я» (*)))}+

+ Ц/

-(*»(*). ^(^(0))+(

аУ1(

а(0)

)'/(А:

(0.

(**(')))}

Ц^з

<*-»(*).

+ {

dVA

a°

(t))

)'f(x

(t)>

")}

+ ЦЛ

<*"(')-

«)

+ (

аУ,(

(0)

)7(А:

(<). и)

d.x

Заметим, что последнее неравенство будет выполняться вдоль

решения x

(t) для каждого x^\t

.7"]

и почти всех t£\x, T] при

Ko =

ho(*)

= Vi(x

W)-W (

2)-

Здесь /г°(т)—гарантированный максиминный выигрыш 1-го

игрока в игре

(33) —

(34) с начальной позицией {т,

(т)}.

В п. 3.4 настоящего параграфа приведен явный вид, арбитраж-

ного решения в линейно квадратичной дифференциальной игре,

полученный в [249] с помощью этого замечания.

3.3.

Достаточные условия. Здесь ограничиваемся щ(х)—

позиционными управлениями /-го игрока (i=

2), удовлетво-

ряющими требованиям из п. 1.4, б) § 1. Предполагаем, что

функции f(x, и) и Fi(x, и) в

(33) — (34)

непрерывны при хвХ

UiBUi

(i—l, 2). Пусть для каждой позиции {/, х} найдены

функции

(х)

такие, что

(x)=

max min XF^x^), и

(х(х)), u

(x(x)))dr

= l, 2),

"il-l

UN\il\

где x(x), t<x<T

—

решение (33) при u = u(x), x(x)==x.

Теорема (Лайу 1293]). Пусть существует счетное разбие-

ние 3) множества X, функции Vi{x) и V]{x) (i=l, 2) непре-

рывно дифференцируемые относительно -

и набор позиционных

управлений u

(x) = {uf(х), Щ(х)} такие, что 1) V

(x) = Q при

всех {Г, JC}6M(3); 2) T/i (x) > V] (х) при х£Х; 3) для всех х£Х

и ufiUi

2) выполнено неравенство:

>•(*,

и)

(Щ£>)'/(х,

u)]-\V

{x)-Vl(x)] +

(X,

+ (^&)'f(x,u)]'\V

(x)--V

(x)]<

>•(*• и*(х)) + (Щ^)'/(х, u?(x))].\V

(x)-V*(x)] +

(x,

(x)) + (^fP)'f(x, u-(x))].lV

(x)~V"

(x)];

4—4150

4) при всех х£Х F

{x, u"(x)) -f (Щ^)'f(x, u

(х))=Ъ

(*=-1,

2).

Тогда набор позиционных управлений и

{х) является реше-

нием Нзша для игры

(33) —

(34).

Доказательство [293] основано на достаточных условиях из.

теории оптимального управления, полученных Сталфордом в

[344].

3.4. Линейно квадратичные игры. Предполагаем, что выпол-

нены требования к

(31) —(32)

и классу позиционных управле-

ний из п. 1.6 § 1 и Q=0 (t=l, 2). Запишем

(31)

—(32) в виде

(-V-2)

x=A(t)x+B(t)u,

h{u

) = ~l [x'QiX

u'R<tu]dt

(t=l, 2).

Здесь B = ^ в]' %

i==

R-

' -~-У

сть с

помощью Функций

V°

(x)

-K-x

Q°i(t)x

и Vl (.*:)—-

—

x'$>(t)x найдены максиминные.

позиционные управления соответственно в задачах:

./?==

maxmin/i(«i[•],

th[-]),

/2-=maxmm/

(«iH'

%["!)•

«л-i ««[•]

"2l'l «iH

Функции Vi

(x)

—

(*•)

(i —

2) пусть найдены с помощью*

замечания, приведенного нами в п. 3.2. § 3 после формулировки?

необходимого условия существования арбитражного решения из

[249].

Тогда решение Нэша в классе программных управлений

имеет вид

г 2

где

««(/)= —

2м*)д,(*)

./-=i

-'(О

2 м*)

мо

7-1

(*).

(*)

= у

-*"

* W

* М-

)

(7, * =

1 -

7 -£

< t < 0-

Замечания. Арбитражное решение Нэша обладает рядом,

«хороших» игровых свойств: оптимальность по Парето, симмет-

рия (при равных условиях игроки получают одинаковые вы-

игрыши), инвариантность относительно аффиных преобразова-

ний функций выигрыша (арбитражное решение не изменится,.

если вместо (34) рассмотреть функции выигрыша вида cJi + di,.

где

•£•!•=

Const>0,

di—Const), независимостью относительно не-

существенных альтернатив [89]. Эти свойства и объясняют-

стремление авторов ряда статей выбрать арбитражное решение.-

Нэша в качестве решения многокритериальной задачи опти-

мального управления. Такой подход использовали Прасад иг

Сарма

[317],

Л. И. Кожинская и Л. И. Слуцкий [77], Клемхоу*,

Лейтмэн и Ван

[214].

Обобщение на стохастические системы

обсуждается в

[316].

Особо интересен случай, когда равновес-

ное (по Нэшу) решение совпадает с решением Нэша. Наличие

его обнаружено Клемхоу, Ваном и Лейтмэном в задаче о «де-

леже пирога»

[214].

3.5.

Оптимальные стратегии угроз. В этом разделе предпо-

лагаем, что в игре

(33) — (34)

выпукло и компактно множество

когда набор управляющих воздействий {ux[t], %[/]} пробегает

все возможные значения. В арбитражной схеме Нэша в каче-

стве точки «статус кво» {/Д h

} берутся гарантированные

(максиминные) выигрыши игроков. Затем выигрыши игроков

находятся максимизацией функции (h{u)—Ii°)(I

(u)—/

°). Од-

нако выигрыши игроков можно изменить, варьируя начальную

точку {/Д

Именно, будем предполагать, что игра проис-

ходит в два этапа.

На первом этапе игроки, независимо друг от друга, выби-

рают «свои» управляющие воздействия tiri

[t]

(.1=1,

2). Пусть

= h(^i

['], u

[-])—соответствующие выигрыши игроков

(-=1,2).

На втором этапе игроки совместно выбирают набор управ-

ляющих воздействий

и* [t]

= {иЦЦ,

[t]}

согласно арбитражной

схеме Нэша

(/i-/i)(/2-/f)= max (А{и[.])-/i)(/

(a[•])-/!).

Итак, управляющие воздействия и\

Щ (.£

2) используются,

прежде всего, для нахождения точки {If, Щ и затем уже при

отыскании выигрышей {/J, l\). Таким образом, в конечном счете,

It (i-=l,2) можно рассмотреть как функционалы, зависящие

от

и?Щ

= {иЦЩМ\Л),

= 1 №\ЛМ\Л)

(--

= -• 2).

Определение (Лайу [292]). Набор управляющих воз

действий {ui [t\, ul

[t]}

называется оптимальными стратегиями

угроз для игры (33)

—(34),

если

/i(^[-I,S[-])>7iW[-],a[-]).

^(ам,й1-1)>?

(и?[-ь^[-])

для любых управляющих воздействий

{и

Щ,

Щ Щ}.

Таким об-

разом, оптимальные стратегии угроз реализуют равновесное (по

Нэшу) решение в классе управляющих воздействий

{Щ

[t\,

Лайу в статье [292] для нахождения оптимальных стратегий

угроз и соответствующих выигрышей

I'\

= /i

(a?

[ •

])

предложил

следующие достаточные условия: если существует постоянная

0<[х< оо и два набора управляющих воздействий {#*,

и*

)

{tii,

u%}

такие, что

(и*,

tt*)-f

\il

(tf

йр==тах[/

(и

)

!я/

(й1'

«г)].

(и

U2)-~\xI

(tti,

и")

= minmax[Ii(u

)~\i1

щ)]

«2 Щ

max

min[Л(й-,

)

—

\xl

щ)]>

(Л,

t&) —

ji (Й, Й)

—

(J.

(•«*»

ий — /2

(Й, ul)),

то набор {«I, aj»} — оптимальные стратегии угроз для игры

(33) —

(34),

а соответствующие выигрыши l\=l\{ui,

и»)

—Ii(uf,

u!{)

—1,2).

Применим это утверждение к линейно квадратичной игре

вида

x = Ax-\-Bitti-\-B

, x(t

) = x

(щ,

)

= х'

(Т)

x (T)-f [(x'Q

x-f и^я*) dt (i-1,2),

где все используемые матрицы постоянны, причем Ci<0, Q

(постоянно отрицательны), a ./?i<0 (определенно отрицательны).

Игроки используют программные управления wi(^), £

<^<7\

подчиненные условию \ ||

щ (t) ||

dt < 00 (i= l, 2). Пусть сущест-

во

вует

\i —

Const >

такая, что

B[ - -

R2~

—

|АС

О,

C&R^B.C, = ^C^RT'B

;C„.

Тогда [292] выигрыши игроков при использовании ими оптималь-

ных стратегий угроз определяются следующими равенствами

/:=л(й,

Й)=1Х;[Л(^+-

2^О)1^,

/; - /

(а.

а)

1Л

<*<>)

-°

сад

*<••

Здесь матрицы /-*-(£) и Р

(^ —решения соответственно систем

Л - -

РгА

- А'Р

4 Pi (B

4 j B

) P

—

-(Qi+^Q

)=0,

—

- P

—

A'P

[B^T'B'i -15

^;)

—

~(Qi-!^Q

)

—