Турчина Н.В. Физика в задачах для поступающих в вузы
Подождите немного. Документ загружается.

550
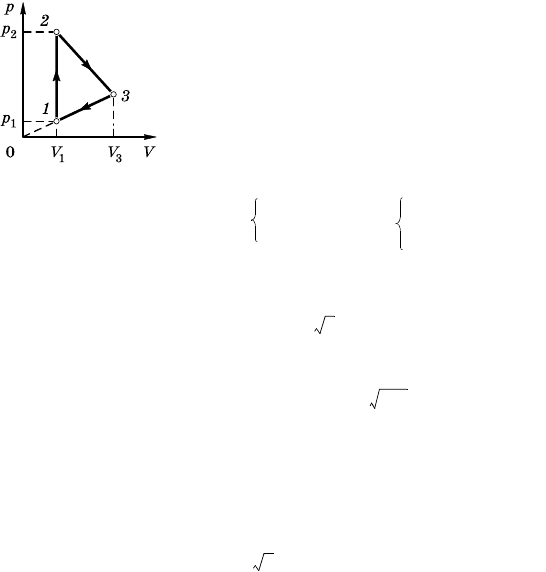
Процесс 2–3 изобарный, поэтому
Q
2–3
= ∆U
2–3
+ A
2–3
= p
2
∆V + p
2
∆V = p
2
∆V =
= αp
0
∆V=(β –1)αp
0
V
0
.(4)
Следовательно, подведенное в циле оличество теплоты
Q = Q
1–2
+ Q
2–3
.(5)
Из уравнений (1)—(5) получим
η = = .
О т в е т: η = 4/23.
9.11.12. КПД цила (рис. 9.11.16)
η =. (1)
Работа аза за цил
A =(p
2
– p
1
)(V
3
– V
1
)= (n –1) –1 .
Та а процесс 3–1 линейный, то можно
записать:
⇒
де k — оэффициент пропорциональности.
Следовательно,
A = ( – 1). (2)
Процесс 2–3 линейный и T
2
= T
3
, поэтому ∆U
2–3
= 0, а
Q
2–3
= A
2–3
=(V
3
– V
1
)= (n –1).
Процесс 1–2 изохорный; A
1–2
= 0 и Q
1–2
= ∆U
1–2
, т. е.
Q
1–2
= R(T
2
– T
1
)= RT
1
(n –1).
Работа аза за цил
А = 3Q
1–2
= 90 Дж.
3
2
---
5
2
---
5
2
---
5
2
---
2 α 1−()β 1−()
5αβ 2α− 3−
----------------------------------------
4
23
------
Рис. 9.11.16
A
Q
1
------ -
1
2
---
RT
1
2
-----------
⎝
⎛
V
3
V
1
------
⎠
⎞
p
1
= kV
1
,
p
2
= kV
3
kV
1
2
= RT
1
,
kV
2
2
= RT
2
,
RT
1
n 1−()
2
------------------------------
n
p
2
p
3
+
2
----------------- -
RnT
1
2
------------------- -
3
2
---
3
2
---
n 1−()
551
Количество теплоты, полученное азом за цил,
Q
1
= Q
1–2
+ Q
2–3
=(n –1)( +n). (3)
Решив систему уравнений (1)—(3), находим
η = · 100% = 20%.
О т в е т: A = 90 Дж; η = 20%.
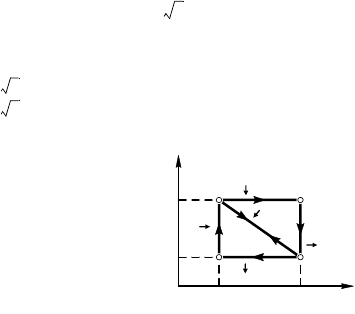
9.11.13. КПД цила 1–2–4–1
(рис. 9.11.17)
η
1
=;
КПД цила 2–3–4–2
η
2
=.
Работа А за цил одинаова для обо-
их цилов:
A =(p
2
– p
1
)(V
2
– V
1
).
Количество теплоты, полученное в циле 1–2–4–1,
Q
1–2
+ Q
2–4
= Q
1–4
+ A,
де Q
1–3
= ∆U
1–4
+ A
1–4
= p
1
(V
2
– V
1
).
Количество теплоты, полученное в циле 2–3–4–2,
Q
2–3
= ∆V
2–3
+ A
2–3
= p
2
(V
2
– V
1
).
Решив систему приведенных уравнений, находим о т в е т:
η
2
= и = 1 + 4η
1
= 2,5.
9.11.14. КПД цила 1–2–3–1
η
1
=. (1)
Количество теплоты, получаемое азом за цил,
Q
1
= ∆U
1–3
+ A
2–3
. (2)
RT
1
2
-----------
3
n 1−
n 1+
-----------------
0
1
2
4
3
p
VV
1
Q
1,2
Q
3,4
Q
2,3
Q
2,4
Q
1,4
V
2
p
1
p
2
Рис. 9.11.17
A
θ
12−
θ
24−
+
---------------------------- -
A
Q
23−
------------
1
2
---
5
2
---
5
2
---
η
1
14η
1
+
------------------- -
p
2
p
1
------
A
Q
1
------ -
552
КПД цила 1–3–4–1
η
2
=. (3)
Работа, совершаемая аждой машиной за цил, одинаовая.
Количество теплоты, получаемое азом в циле 1–3–4–1,
= ∆U
1–3
+ A
1–3
.(4)
Работа, совершаемая в процессе 2–3 первой машиной, больше
работы, совершаемой в процессе 1–3 второй машиной:
A
2–3
= A
1–3
+ A.(5)
Решив систему уравнений (1)—(5), получим о т в е т :
η
2
=.
9.11.23. При изотермичесом расширении аза (процесс 1–2)
внутренняя энерия аза не изменяется, и подведенное оличество
теплоты Q
1–2
равно работе A
1–2
, совершаемой азом. При изохорном
охлаждении (процесс 2–3) изменение внутренней энерии ∆U
2–3
=
=– νR∆T . В адиабатном процессе 3–1 теплообмен аза с ору-
жающей средой отсутствует, т. е. A
3–1
+ ∆U
3–1
= 0. Та а тем-
пературы в точах 1 и 2 одинаовы, то ∆U
3–1
=–∆U
2–3
= νR∆T. По-
этому A
3–1
= –∆U
3–1
= – νR∆T. Коэффициент полезноо действия
η = = ,
отуда получаем
A
1–2
= d 12,5 Дж.
О т в е т: A d 12,5 Дж.
9.12.7. КПД цила
η =, (1)
де Q
1
– оличество теплоты, подведенное рабочему телу. Та а
по условию машина является идеальной, то
η = = . (2)
A
Q
1
′
-------
Q
1
′
η
1 η+
------------ -
3
2
---
3
2
---
3
2
---
A
12−
A
31−
+
Q
12−
------------------------------ -
A
12−
3
2
--- νR∆ T−
A
12−
---------------------------------------
3νR∆T
21 η−()
----------------------
A
Q
1
------ -
T
1
T
2
−
T
1
--------------------
Q
1
Q
2
−
Q
1
--------------------

553
Сравнивая выражения (1) и (2), получим A = Q
1
– Q
2
, отуда
Q
1
= A + Q
2
. Тода η =; η =18%.
О т в е т: η = 18%.
9.12.15. Пусть КПД тепловой машины η = , а КПД холо-
дильной машины η′ = . Тода за счет оличества теплоты Q со-
вершается работа A = ηQ, а помещению передается оличество теп-
лоты Q′ = . Отсюда
== =3,
т. е. от сорания дров в пече помещение получит в 3 раза меньшее
оличество теплоты, чем при отоплении ео холодильной машиной.
Ответ: Q′/Q = 3.
9.12.16. Тепловая машина получает оличество теплоты от на-
ревателей на участах изотермичесоо расширения 1–2 и 3–4, а
отдает оличество теплоты на участе изотермичесоо сжатия 5–6–7.
Поэтому КПД машины
η = = ,
де A
1–2–3–4–5–6–7–1
— работа за цил.
Рассмотрим процессы 1–2–3–6–7–1 и 3–4–5–6–3. Оба процес-
са — цилы Карно. Поэтому КПД тепловых машин соответствен-
но равны
η
1
= = ,
η
2
==,
де A
1–2–3–6–7–1
=2 A
3–4–5–6–3
, или
η
1
=, η
2
=
(здесь T
1
= t
1
+ 273, T
2
= t
2
+ 273, T
3
= t
3
+ 273).
A
AQ
2
+
-----------------
T
1
T
2
−
T
1
--------------------
T
1
′
T
2
′
−
T
1
′
-------------------- -
A
η
′
-----
Q
′
Q
-----
ηA
η
′
A
-------- -
T
1
T
2
−()T
1
′
Q
′
T
1
′
T
2
′
−()T
1
Q
---------------------------------------
Q
12−
Q
34−
Q
56− 7−
−+
Q
12−
Q
34−
+
-----------------------------------------------------------
Q
12− 3− 4− 5− 6− 7− 1−
Q
12−
Q
34−
+
--------------------------------------------- -
Q
12−
Q
67−
−
Q
12−
------------------------------------- -
A
12− 3− 6− 7− 1−
Q
12−
-------------------------------------------
Q
34−
Q
56−
−
Q
34−
------------------------------------- -
A
34− 5− 6− 3−
Q
34−
----------------------------------- -
T
1
T
3
−
T
3
--------------------
T
2
T
3
−
T
2
--------------------

554
Следовательно,
=, =.
Работа в процессе 1–2–3–4– 5 –6–7–1 равна
A
1–2–3–4–5–6–7–1
= A
1–2–3–6–7–1
+ A
3–4–5–6–3
=3A
3–4–5–6–3
,
а оличество теплоты, полученное от наревателя,
Q
1–2
+ Q
3–4
=+=
= A
3–4–5–6–3
+ .
Следовательно,
η = = = 0,33.
О т в е т: η = 0,33.
9.13.8. Из уравнения Клапейрона—Менделеева плотность су-
хоо воздуха: ρ
сух
=.
Давление влажноо воздуха по заону Дальтона равно сумме
парциальных давлений сухоо воздуха p
1
и водяноо пара p
2
:
p
вл
= p
1
+ p
2
.
Давление паров воды p
2
= ϕp
н
. Плотность влажноо воздуха
ρ
вл
= ρ
1
+ ρ
2
, де ρ
1
— плотность воздуха без водяных паров, ρ
2
—
плотность пара.
Запишем уравнение Клапейрона—Менделеева соответственно
для сухоо воздуха и для пара:
p
1
= RT, p
2
=.
Отсюда находим плотность влажноо воздуха:
ρ
вл
=
A
12− 3− 6− 7− 1−
Q
12−
-------------------------------------------
T
1
T
3
−
T
1
--------------------
A
34− 5− 6− 3−
Q
34−
----------------------------------- -
T
2
T
3
−
T
2
--------------------
A
12− 3− 6− 7− 1−
T
1
T
1
T
3
−
-------------------------------------------------- -
A
34− 5− 6− 3−
T
2
T
2
T
3
−
-------------------------------------------
⎝
⎛
2T
1
T
1
T
3
−
--------------------
T
2
T
2
T
3
−
--------------------
⎠
⎞
3A
34− 5− 6− 3−
A
34− 5− 6− 3−
2T
1
T
1
T
3
−
--------------------
T
2
T
2
T
3
−
--------------------
+
⎝⎠
⎛⎞
------------------------------------------------------------------------------------------
3 T
1
T
3
−()T
2
T
3
−()
3T
1
T
2
T
2
T
3
− 2T
1
T
3
−
----------------------------------------------------------------
ρ
0
M
в
RT
-------------- -
ρ
1
M
в
--------
ϕρ
н
M
п
RT
------------------
M
в
p
0
ϕp
н
−()ϕM
п
p
н
+
RT
---------------------------------------------------------------
555
и отношение плотностей сухоо и влажноо воздуха:
= d 1,0046.
Ответ: d 1,0046.
9.13.10. Из уравнения Клапейрона—Менделеева найдем плот-
ность сухоо воздуха:
ρ
сух
=.
Давление влажноо воздуха (по условию р
вл
= р
0
) по заону
Дальтона равно сумме парциальных давлений воздуха без пара p
1
и
водяноо пара p
2:
p
0
= p
1
+ p
2
.
Давление водяных паров и давление воздуха без пара равны
соответственно
p
2
= ϕp
н
,
p
1
= p
0
– p
2
= p
0
– ϕp
н
.
Плотность влажноо воздуха
ρ
вл
= ρ
1
+ ρ
2
,
де ρ
1
и ρ
2
— плотность воздуха без водяных паров и плотность пара
соответственно.
Используя уравнение Клапейрона—Менделеева для сухоо воз-
духа и насыщенноо пара:
p
1
= RT, p
н
= RT,
получим
ρ
1
==– , ρ
2
= ϕρ
н
=.
Найдем плотность влажноо воздуха:
ρ
вл
=+.
ρ
сух
ρ
вл
----------
p
0
p
0
ϕp
н
1 M
п
/M
в
−()−
-----------------------------------------------------------
ρ
сух
ρ
вл
----------
p
0
μ
2
RT
------------
ρ
1
μ
2
----- -
ρ
н
μ
1
----- -
μ
2
p
1
RT
------------
μ
2
p
0
RT
------------
ϕμ
2
p
н
RT
-----------------
ϕp
н
μ
1
RT
-----------------
μ
2
p
0
ϕp
н
−()
RT
--------------------------------- -
ϕμ
1
p
н
RT
-----------------

556
Используя условие задачи, получим
ρ
вл1
=+,
ρ
вл2
=+,
∆ρ
вл
= ρ
вл1
– ρ
вл2
=– – d 46 /м
3
.
О т в е т: ∆ρ
вл
d 46 /м
3
.
9.13.14. Масса воды, оторую испарили,
m = m
2
– m
1
,(1)
де m
2
— масса паров воды, оторая будет в баллоне после испаре-
ния воды (в онечном состоянии); m
1
— масса паров в баллоне в на-
чальном состоянии.
Запишем уравнение Клапейрона—Менделеева для начальноо и
онечноо состояний паров воды:
pV = RT,(2)
p
н
V = RT. (3)
Абсолютная влажность
ρ =. (4)
Решив систему уравнений (1)—(4), получим о т в е т :
ρ =–d 13 /м
3
.
9.13.15. Давление в сосуде при t
2
=127°C равно
p =+p
2
,
де — давление сухоо воздуха: = p
1
; p
2
— давление паров
воды.
Найдем p
2
из уравнения Клапейрона—Менделеева, предполо-
жив, что весь лед испарится:
p
2
= = 6,64 · 10
4
Па.
μ
2
p
0
ϕ
1
p
н1
−()
RT
1
---------------------------------------
ϕ
1
μ
1
p
н1
RT
1
--------------------- -
μ
2
p
0
ϕ
2
p
н2
−()
RT
2
---------------------------------------
ϕ
2
μ
1
p
н2
RT
2
--------------------- -
μ
1
p
0
T
2
T
1
−()
RT
1
T
2
--------------------------------------
μ
1
μ
2
−
R
------------------
⎝
⎛
ϕ
1
p
н1
T
1
---------------
ϕ
2
p
н2
T
2
---------------
⎠
⎞
m
1
μ
--------
m
2
μ
--------
m
1
V
--------
μp
н
RT
----------
m
V
---- -
p
1
′
p
1
′
p
1
′
T
2
T
1
-------
mRT
2
MV
---------------- -

557
Посольу p
2
< p
н
, то весь лед действительно испарится. Оонча-
тельно получим
p = p
1
+ = 2,26 · 10
5
Па.
О т в е т: p = 2,26 · 10
5
Па.
9.13.17. Та а пар в обеих частях сосуда насыщенный, то в на-
чальном состоянии плотность пара в левой части равна ρ
н1
=
= 0,0173 /м
3
, а в правой ρ
н2
= 0,083 /м
3
(из табличных дан-
ных). Если переороду убрать, то
ρ = = 0,0508 /м
3
.
Та а основная часть пара находится в более наретой поло-
вине, то можно предположить, что пар, ода уберем переороду,
будет ненасыщенным. Тода по заону сохранения энерии
RT
1
+ RT
2
=+RT,
де m
1
, m
2
— массы пара в левой и правой частях сосуда соответст-
венно равны:
m
1
= ρ
н1
, m
2
= ρ
н2
(здесь V — объем сосуда).
Решив систему приведенных уравнений, получим
T ==317,8К; t =44,8°С.
Действительно, t = 44,8 °С>40°C, следовательно, пар ненасы-
щенный и ео давление
р = = 7453 Па.
9.14.5. Запишем уравнение Клапейрона—Менделеева для на-
чальноо состояния пара:
pV = RT
1
,(1)
де m
1
— масса пара в начальном состоянии.
T
2
T
1
-------
mRT
2
μV
---------------- -
ρ
н1
ρ
н2
+
2
------------------------
im
1
2μ
----------
im
2
2μ
----------
i
2
---
⎝
⎛
m
1
μ
--------
m
2
μ
--------
⎠
⎞
V
2
---
V
2
---
ρ
н1
T
1
ρ
н2
T
2
+
ρ
н1
ρ
н2
+
-------------------------------------- -
ρ
н1
ρ
н2
+()RT
2μV
------------------------------------- -
m
1
μ
--------

558
В онечном состоянии пар будет насыщенным (это можно доа-
зать), и уравнение Клапейрона—Менделеева для этоо состояния
имеет вид:
p
н
V = RT
2
,(2)
де m
2
— масса пара в онечном состоянии.
Масса росы, выпавшей на стенах труби,
∆m = m
1
– m
2
.(3)
Решив систему уравнений (1)—(3), получим
∆m =–d 9,65 · 10
–6
.
О т в е т: ∆m d 9,65 · 10
–6
.
9.14.17. Если влажность воздуха 80% (рис. 9.14.2, состояние а),
то подъемная сила шара равна нулю. Запишем первый заон Ньютона
для проеций сил на ось ОY:
F
A1
– mg =0,
де m — масса воздушноо шара (общая); F
A1
— сила Архимеда,
равная:
F
A1
= ρ
вл
gV;
ρ
вл
— плотность влажноо воздуха:
ρ
вл
= ρ
возд
+ ρ
п
;
ρ
возд
— плотность сухоо воздуха:
ρ
возд
=;
m
2
μ
--------
μV
R
-------
⎝
⎛
p
T
1
-------
p
н
T
2
-------
⎠
⎞
Y
O
F
A
1
mg
Y
O
F
A
2
mg
a
а)
б)
Рис. 9.14.2
p ϕp
н
−()μ
возд
RT
--------------------------------------

559
p
н
— давление паров воды; ρ
п
— плотность паров воды:
ρ
п
=.
Если влажность ϕ→0 (рис. 9.14.2, состояние б), то
F
A2
– mg = та,
де F
A2
— сила Архимеда:
F
A2
= ρ
2
gV,
ρ
2
— плотность воздуха. Если воздух сухой, то ρ
2
=.
Решив систему приведенных уравнений, получим
a = g = 0,39 м/с
2
.
О т в е т: a = 0,39 м/с
2
.
9.14.18. По условию задачи внешнее давление постоянно, темпе-
ратура уменьшается. Следовательно, уменьшается давление в сосуде,
поэтому сила давления будет направлена внутрь баллона и равна:
F =(p
0
– p
2
) πr
2
,
де p
2
— давление в сосуде при температуре t
2
=10°C:
p
2
= p
2в
+ p
2п
(p
2в
— давление воздуха, p
2п
— давление пара).
Та а объем не изменяется, то давление воздуха при темпера-
туре t
2
=10°C и начальное давление воздуха в сосуде связаны соот-
ношением
=,
де p
1в
— давление воздуха при температуре t
1
=40°C:
p
1в
= p
0
– ϕ p
1н
,
ϕp
1н
— давление паров воды при температуре t
1
=40°C.
Давление паров воды при температуре t
2
=10°C:
p
2п
= p
2нас
,
де p
2нас
— давление насыщенноо пара при t
2
=10°C.
Решив систему приведенных уравнений, получим
F = p
0
1– +ϕ p
1н
– p
2н
πr
2
=37,7Н.
О т в е т: F = 37,7 H.
ϕp
н
μ
H
2
O
RT
--------------------- -
p
0
μ
возд
RT
-------------------
ϕp
н
μ
возд
μ
H
2
O
−()
p
0
μ
возд
ϕp
н
μ
возд
μ
H
2
O
−()−
----------------------------------------------------------------------- -
p
1в
T
1
------- -
p
2в
T
2
--------
-
⎝
⎛
T
2
T
1
-------
⎠
⎞
T
2
T
1
-------
