Турчина Н.В. Физика в задачах для поступающих в вузы
Подождите немного. Документ загружается.

540
9.3.4. КПД чайниа η =, де Q
п
— полезное оличество теп-
лоты, оторое идет на наревание воды до температуры ипения t
и испарение воды:
Q
п
= cm(t
– t)+rm
(m = ρV — масса воды), Q
з
— энерия, получаемая наревателем от
сети:
Q
з
= ηN.
Из приведенных уравнений получим о т в е т:
τ = d 3ч.
9.5.14. Температуру θ
1
воды в первом сосуде после первоо пе-
реливания найдем из уравнения тепловоо баланса:
ρV
0
c (θ
1
– t
1
)=ρ(V – V
0
) c (t
2
– θ
1
), θ
1
=
(ρ — плотность воды, c— удельная теплоемость воды), а темпера-
туру θ
2
воды во втором сосуде после переливания остывшей воды из
первоо сосуда — из уравнения
2ρ(V – V
0
) c (θ
2
– θ
1
)=ρ(2V
0
– V) c (t
2
– θ
2
), θ
2
=.
После второо переливания температура воды в сосудах будет
отличаться на
∆t
2
= θ
2
– θ
1
==t
2
.
После следующео переливания воды из второо сосуда в первый
2ρ(V – V
0
) c (θ
2
– θ
3
)=ρ(2V
0
– V) c (θ
3
– θ
1
), θ
3
=,
∆t
3
= θ
3
– θ
2
==t
2
,
а обратно
ρ(2V
0
– V) c (θ
2
– θ
4
)=2ρ(V – V
0
) c (θ
4
– θ
3
), θ
4
=,
∆t
4
= θ
4
– θ
3
= t
2
.
Q
п
Q
з
------ -
ρVct
t−()r+[]
ητ
------------------------------------------- -
t
2
3
---- -
5t
2
9
---------
2t
2
9
---------
2
3
2
----- -
13t
2
27
------------
2t
2
27
---------
2
3
3
----- -
41t
2
81
------------
2
3
4
----- -
541
После n-о переливания воды ∆t
n
= t
2
. Посольу ∆t
n
m 1 °C, то
m 0,01, n l 5.
О т в е т: n l 5.
9.5.19. 1-й сосуд. Количество теплоты, необходимое льду для
наревания до температуры плавления t
пл
=0°C:
Q
л
= c
л
m
1
(t
пл
– t
л
) = 47,25 Дж.
Вода при этом должна остыть до таой же температуры,
Q
в
= c
в
m
в1
(t
1
– t
пл
)=c
в
ρ V
1
(t
1
– t
пл
)=12,6Дж,
де m
в1
= ρV
1
— начальная масса воды в сосуде, ρ — плотность
воды.
Посольу Q
л
> Q
в
, то лед, получив оличество теплоты Q
в
за
счет остывания воды, не нареется до t
пл
.
Найдем оличество теплоты Q′
в
, оторое может быть передано
льду при замерзании воды:
Q′
в
= m
в1
λ = ρV
1
λ =165Дж.
Сравнивая Q
л
с Q
в
+ , видим, что Q
л
< Q
в
+ . Следователь-
но, для наревания льда до температуры t
пл
вода в первом сосуде
должна остыть и часть ее превратится в лед при t
пл
.
Из уравнения тепловоо баланса
Q
л
= Q
в
+ λ
найдем массу замерзшей воды:
= d 0,1 .
Во второй сосуд перелили воды при температуре t =0°C:
∆m =(m
в1
–)=(ρV
1
–)d 0,2 .
2-й сосуд. Лед находится при температуре плавления. Коли-
чество теплоты, необходимое для плавления,
= m
2
λ =148,5Дж.
2
3
n 1+
-------------
2
3
n 1+
-------------
Q
в
′
Q
в
′
m
в1
′
m
в1
′
m
в1
′
Q
л
Q
в
−
λ
--------------------
1
2
---
m
в1
′
1
2
---
m
в1
′
Q
л
плав
542
Это оличество теплоты может быть получено за счет остыва-
ния воды до t =0°C:
= c
в
ρV
2
(t
2
– t
пл
) = 151,2 Дж.
Та а > , то весь лед растает и образовавшаяся во-
да нареется. Поэтому
+ c
в
m
2
(θ – t
пл
)+c
в
∆m(θ – t
пл
)=c
в
ρV
2
(t
2
– θ),
отуда
θ = d 0,11 °C.
О т в е т: θ d 0,11°C.
9.5.20. При тепловом равновесии в сосуде будет находиться во-
да при неоторой температуре θ, оторую можно найти из уравне-
ния тепловоо баланса:
c
1
m
1
(t
пл
– t
1
)+c
2
m
2
(t
пл
– t
1
)+λm
2
+ c
1
m
1
(θ – t
пл
)+cm
2
(θ – t
пл
) =
= c
3
m
3
(t
2
– t
ип
)+ρm
3
+ cm
3
(t
ип
– θ) ⇒ θ =36,6°C.
О т в е т: θ = 36,6 °C.
9.5.21. Для образования пара необходима энерия Q
1
= rm
п
,
оторая будет получена за счет образования льда Q
2
= ∆mλ (здесь r —
удельная теплота парообразования, λ — удельная теплота плавле-
ния). Учтем, что m
п
= m – ∆m. Из приведенных уравнений получим
∆m = = 17,2 .
О т в е т: œm = 17,2 .
9.7.12. Из уравнения Клапейрона—Менделеева
pV = νRT
и заона, по оторому расширяется аз, p = (см. условие) найдем
зависимость температуры аза от объема:
T =.
Следовательно, при увеличении объема в n раз температура
уменьшится в n раз:
T =. (1)
Q
в
ост
Q
в
ост
Q
л
плав
Q
л
плав
c
в
ρV
2
t
2
Q
л
плав
−
c
в
m
2
∆m ρV
2
++()
-------------------------------------------------- -
mr
r λ+
----------- -
α
V
2
------
α
νRV
----------- -
T
0
n
-------
543
Изменение внутренней энерии
∆U = νR (T – T
0
). (2)
Решив систему уравнений (1), (2) (учтем, что энерия убывает),
получим о т в е т:
T
0
= = 300 К.
9.7.18. Система «сосуд—поршень—аз» замнута, и по заону
сохранения импульса
mv =(m + M + m
) u,
де m
— масса аза в сосуде, u — сорость движения системы после
преращения олебаний поршня.
Разность инетичесих энерий системы в начале и онце дви-
жения сосуда равна энерии, отданной азу:
mv
2
–(m + M + m
)u
2
= ∆E.
Та а масса аза в сосуде m
n
М
и масса сосуда m n M, то
∆E =.
Энерия, отданная азу, пойдет на увеличение ео внутренней
энерии:
∆E = ∆U.
Изменение внутренней энерии аза
∆U =2
.
νR∆T =3νR∆T.
Из приведенных уравнений находим
∆T = d .
О т в е т: œT d .
9.7.22. Энерия аза в первом сосуде равна U
1
= p
1
V
1
, во вто-
ром U
2
= p
2
V
2
. Энерия аза в обоих сосудах после их соединения
U = p (V
1
+ V
2
). По заону сохранения энерии
U
1
+ U
2
= U.
3
2
---
2n∆U
3νRn 1−()
------------------------------
1
2
---
1
2
---
mM m−()v
2
2M
-----------------------------------
3
2
---
mM m−()v
2
6νMR
-----------------------------------
mv
2
6R
-----------
mv
2
6R
-----------
3
2
---
3
2
---
3
2
---
544
Следовательно, давление аза в обоих сосудах
p =. (1)
Объединенный азовый заон для аза, находящеося в первом
сосуде:
=, (2)
для аза во втором сосуде:
=. (3)
По заону Дальтона
p =+. (4)
Решив систему уравнений (1)—(4), найдем температуру аза
T = T
1
T
2
.(5)
О т в е т : см. (1) и (5).
9.8.10. Обозначим p — давление, V
0
—
начальный объем аза, а
V = V
0
+ ∆V — онечный объем аза. Запишем уравнение Клапейро-
на—Менделеева для начальноо состояния аза:
pV
0
=.
Работа аза при ео расширении
A = p ∆V = νRT .
Находим отношение
= = 1 + = 6.
О т в е т: V/V
0
= 6.
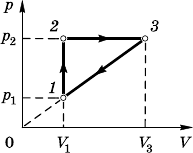
9.8.23. Построим рафи данноо
цила в оординатах p—V (рис. 9.8.13).
Из рафиа цила найдем работу:
A =(V
2
– V
1
).
Запишем уравнение Клапейрона—Мен-
делеева для аждоо состояния аза:
p
1
V
1
= νRT
1
; p
2
V
1
= νRT
2
, p
2
V
3
= νRT
3
.
p
1
V
1
p
2
V
2
+
V
1
V
2
+
--------------------------------
p
1
V
1
T
1
------------ -
p
1
′
V
1
V
2
+()
T
-------------------------------
p
2
V
2
T
2
------------ -
p
2
′
V
1
V
2
+()
T
-------------------------------
p
1
′
p
2
′
p
1
V
1
p
2
V
2
+
p
1
V
1
T
2
p
2
V
2
T
1
+
------------------------------------------------
νRT
V
0
------------
∆V
V
0
--------
V
V
0
------
V
0
∆V+
V
0
-------------------- -
A
νRT
------------
Рис. 9.8.13
p
2
p
1
−
2
----------------- -

545
Для линейноо процесса 1—3 найдем отношение давлений:
=.
Решив систему приведенных уравнений, получим о т в е т:
A =; А d 104 Дж.
9.8.26. Работа аза, совершаемая за один цил,
A = A
12
+ A
23
= A
31
,
де A
12
= 0 (процесс изохоричесий); A
23
=(V
3
– V
2
) (процесс
линейный); A
31
=(V
1
– V
3
) (процесс линейный). Та а про-
цесс 3—1 линейный и рафи ео проходит через начало оорди-
нат, то
===.
Решив систему приведенных уравнений, получим о т в е т:
A =.
9.9.5. Соласно первому началу термодинамии
Q = ∆U + A.(1)
Внутренняя энерия аза в начальном и онечном состояниях
соответственно равна
U
1
= νRT
1
, U
2
= νRT
2
,(2)
де T
1
и T
2
— начальная и онечная температуры. По условию за-
дачи T
2
/T
1
= n, поэтому, используя (2), найдем
= n.(3)
Из уравнения (1) следует, что
U
2
– U
1
= Q – A,
p
1
p
3
------
T
1
T
3
-------
νRT
2
T
1
−()
2
2T
1
------------------------------------
p
2
p
3
+
2
----------------- -
p
1
p
3
+
2
----------------- -
p
1
V
1
------
p
3
V
3
------
T
1
V
2
2
-------
T
2
V
3
2
-------
RT
2
T
1
−()
2
------------------------------
T
2
T
1
-------
1−
3
2
---
1
2
---
U
2
U
1
------ -
546
отуда с учетом соотношения (3) получим
U
1
= = .
О т в е т: U
1
= (Q – A)/3.
9.9.21. Работа аза за весь процесс равна
A = A
1–2
+ A
2–3
+ A
3–4
+ A
4–1
,(1)
де A
1–2
= 0, та а это процесс изохорный; A
2–3
= p
2
(V
3
– V
2
), V
3
и
V
2
— объемы аза в состояниях 3 и 2; A
3–4
= Q, та а это процесс
изотермичесий; A
4–1
= p
1
(V
1
– V
4
), V
1
и V
4
—
объемы аза в состоя-
ниях 1 и 4.
Подставив значения работ в уравнение (1), получим
A = p
2
V
3
– p
2
V
1
+ Q + p
1
V
1
– p
1
V
4
.
Запишем уравнение Клапейрона—Менделеева для аждоо со-
стояния:
p
1
V
1
= νRT
1
, p
2
V
1
= νRT
2
,
p
2
V
3
= νRT
3
, p
1
V
4
= νRT
4
.
Учтем, что T
3
= T
4
. Решив систему приведенных уравнений, на-
ходим
A= νR (T
1
– T
2
)+ Q = 339 Дж.
О т в е т: A = 339 Дж.
9.9.26. Количество теплоты, оторое необходимо сообщить а-
зу, чтобы он перешел из начальноо состояния в онечное,
Q = ∆U = A.(1)
Изменение внутренней энерии
∆U = νR(T
– T
0
).
Работа, совершаемая азом,
A = p
0
(V
– V
0
)=p
0
(3V
0
– V
0
)= p
0
.
2V
0
,
де V
= nV
0
= 3V
0
.
Запишем уравнение Клапейрона—Менделеева для начальноо и
онечноо состояний:
p
0
V
0
= νRT
0
, 3p
0
.
3V
0
= νRT
0
.
QA−
n 1−
--------------
QA−
3
--------------
3
2
---
547
Подставим в уравнение (1) найденные величины:
Q = p
0
V
0
·8+2p
0
V
0
=14p
0
V
0
.
Та а азу уже сообщили оличество теплоты Q
1
=10Дж,
то нужно еще
∆Q = Q – Q
1
, ∆Q =14p
0
V
0
– Q
1
=4Дж.
О т в е т: œQ = 4 Дж.
9.10.11. Процесс 1–2 изобарный, поэтому
Q
1–2
= C
р
ν(T
– T
н
)=–2C
p
νT
0
.
Процесс 3–2 изохорный, поэтому
Q
2–3
= C
V
ν(T
– T
н)
=–C
V
νT
0
.
Та а C
V
= C
p
– R, то
Q
2 – 3
=–(C
p
– R)νT
0
.
Все оличество теплоты, отданное азом в процессе 1–2–3:
Q = Q
1–2
+ Q
2–3
=–νT
0
(3C
p
– R)=–78,7Дж.
О т в е т: Q = –78,7 Дж.
9.10.12. Из первоо начала термодинамии работа равна
A = Q – ∆U,
де оличество теплоты, сообщенное азу, и изменение внутренней
энерии равны соответственно
Q = νC ∆T, ∆U=νC
V
∆T.
Следовательно,
A = νC ∆T – νC
V
∆T =–νR ∆T.
Уравнение Клапейрона—Менделеева для начальноо и онеч-
ноо состояний:
p
1
V
1
= νRT
1
, p
2
V
2
= νRT
2
,
а давления аза в начальном и онечном состояниях в этом процес-
се равны:
p
1
=, p
2
=.
Поэтому
νR∆T = p
2
V
2
– p
1
V
1
=.
3
2
---
α
V
1
2
------
α
V
2
2
------
α V
1
V
2
−()
V
1
V
2
-----------------------------

548
Тода работа расширения аза
A =–νR∆T ==d 1,66 Дж.
О т в е т: A d 1,66 Дж.
9.10.19. Количество теплоты, необходимое для наревания аза,
Q = ∆U + A,(1)
де ∆U = Q
V
.
Найдем зависимость давления от объема в этом процессе:
Та а зависимость давления от объема линейная, то
давление p
cp
= , а работа, совершаемая азом,
A=p
cp
∆V =(V
2
– V
1
).
Учтем, что p = νRαV, и получим
A =–.
Та а T
2
= и T
1
=, то
A =(T
2
– T
1
)= . (2)
При изохорном процессе
Q
V
= c
V
V∆T ⇒ν∆T =. (3)
Решив систему уравнений (1)—(3), получим
Q = Q
V
1+ =580Дж.
О т в е т: Q = 580 Дж.
9.11.6. КПД тепловой машины η = . Работа, совершаемая а-
зом за цил, равна площади, ораниченной линиями цила 1–2–3–1
на p—V-диарамме:
A =(2p
0
– p
0
) (3V
0
– V
0
) = 2p
0
V
0
.(1)
α V
2
V
1
−()
V
1
V
2
-----------------------------
2R
2V
1
----------
pV = νRT,
T = α V
2
⇒
p = νRαV.
p
1
p
2
+
2
----------------- -
p
1
p
2
+
2
----------------- -
VR
2
--------
⎝
⎛
αV
2
2
αV
1
2
⎠
⎞
αV
2
2
αV
1
2
VR
2
--------
VR∆T
2
---------------- -
Q
V
C
V
-------
⎝
⎛
R
2c
V
M
----------------
⎠
⎞
A
Q
1
------ -
549
Процесс 1–2 изохорный: давление увеличивается, температура
увеличивается, поэтому аз в этом процессе получает оличество
теплоты:
Q
1–2
= νR (T
2
– T
1
). (2)
Процесс 2–3 изобарный: объем увеличивается, температура
увеличивается, поэтому аз в этом процессе получает оличество
теплоты, равное
Q
2–3
= ∆V
2–3
+ A
2–3
= νR(T
3
– T
2
)+2p
0
(3V
0
– V
0
). (3)
Запишем уравнение Клапейрона—Менделеева для состояний аза:
p
0
V
0
= νRT
1
,(4)
2p
0
V
0
= νRT
2
,(5)
2p
0
· 3V
0
= νRT.(6)
Количество теплоты, полученное азом за цил:
Q
1
= Q
1–2
+ Q
2–3
.(7)
Решив систему уравнений (1)—(7), получим о т в е т:
η = = 0,087; η =8,7%.
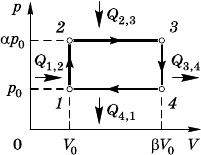
9.11.7. КПД тепловой машины
η =, (1)
де A — работа аза за цил, Q — подведенное оличество теплоты.
Работа за один цил равна площади, ораниченной линиями про-
цессов 1–2–3–4–1 на p—V-диарамме (рис. 9.11.15):
A =(α –1)(β –1)p
0
V
0
.(2)
Для нахождения подведенноо рабо-
чему телу в циле оличества теплоты
рассмотрим последовательно ео участи.
Температуры T
3
> T
2
> T
1
, T
3
> T
4
. Зна-
чит, оличество теплоты подводилось на
участах 1–2 и 3–4, а на участах 3–4 и
4–1 — отводилось.
Процесс 1–2 изохорный, следовательно,
Q
1–2
= ∆U
1–2
= ∆pV
0
=(α –1)p
0
V
0
.(3)
3
2
---
3
2
---
2
23
------
A
Q
1
------ -
Рис. 9.11.15
3
2
---
3
2
---
