Турчина Н.В. Физика в задачах для поступающих в вузы
Подождите немного. Документ загружается.

530
Ч АСТЬ 2
МОЛЕКУЛЯРНАЯ ФИЗИКА
И ТЕРМОДИНАМИКА
Г л а в а 8. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ.
УРАВНЕНИЕ СОСТОЯНИЯ
8.1.8. Количество молеул воды в стаане равно N = . Мо-
лярную массу воды найдем, зная химичесую формулу воды — H
2
O:
M = (16 + 2) · 10
–3
/моль = 18 · 10
–3
/моль.
Таим образом, число вылетающих за 1 с молеул равно
n = = = 4 · 10
18
1/с.
О т в е т: n = 4
.
10
18
c
–1
.
8.3.12. Концентрация молеул n = , де N — число молеул
аза. Плотность аза ρ = , де m — масса вещества: m = m
0
N
(m
0
— масса одной молеулы). Средняя вадратичная сорость мо-
леулы v = .
Решив систему приведенных уравне-
ний, получим о т в е т:
n = = 2,4 · 10
23
м
–3
.
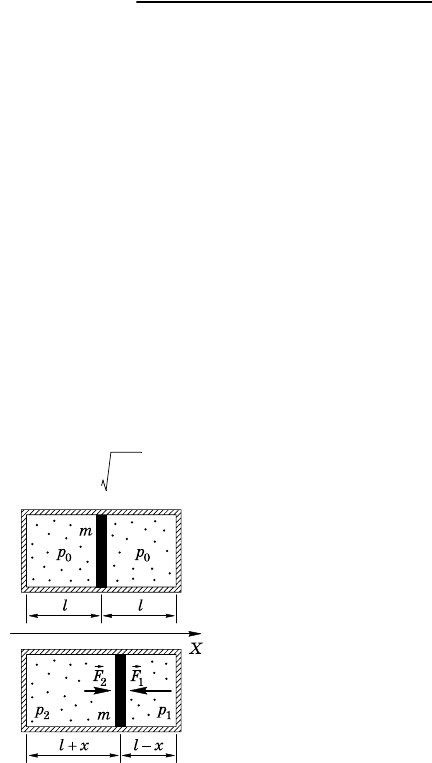
8.4.16. Если поршень сместить впра-
во от положения равновесия, то воздух
справа от поршня будет сжат, а слева —
расширен. Если поршень отпустить, то
он начнет двиаться влево, по инерции
«просочит» положение равновесия и
сожмет воздух в левой части сосуда. Те-
перь поршень станет двиаться вправо и
т. д., т. е. поршень будет совершать оле-
бания (рис. 8.4.10, а).
mN
A
M
--------------
N
t
-----
m
M
----- -
N
A
t
------- -
N
V
-----
m
V
---- -
3kT
m
0
------------
Рис. 8.4.10
а)
б)
ρv
2
3kT
------------
531
Запишем уравнения состояния воздуха в обеих частях сосуда
для положения равновесия поршня и положения, ода поршень
смещен вправо на произвольную величину x (см. рис. 8.4.10, б):
p
0
Sl = ν
1
RT, p
0
Sl = ν
2
RT;
p
1
S(l – x) = ν
1
RT, p
2
S(l + x) = ν
1
RT.
В новом положении поршня разность давлений
∆p = p
1
– p
2
= – ,
и на поршень будет действовать результирующая сила, направлен-
ная положению равновесия:
F = ∆pS = – = d ,
де учтено, что x f l.
Та а F f x, то олебания поршня будут армоничесими.
В этом случае можем записать
– = –kx, T
ол
= 2π .
Следовательно, период олебаний поршня
T
ол
= 2π d 0,44 с.
8.5.7. Обозначим V
2
— онечный
объем аза. При изобарном процессе
= , следовательно, V
2
= V
1
.
Масса аза
m = ρ
2
V
2
= ρ
2
V
1
= 0,0144 .
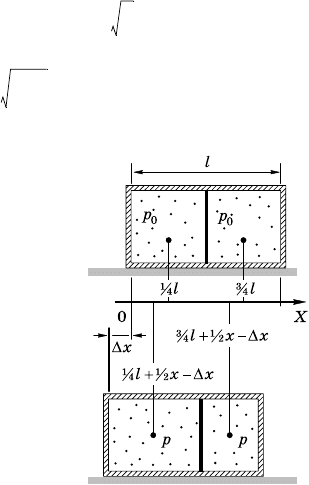
8.7.8. При наревании воздуха в
левой части сосуда и охлаждении в
правой поршень сместится в сторону
более холодноо аза. Центр масс сис-
темы останется на прежнем месте
(рис. 8.7.4). Найдем смещение поршня
внутри сосуда. Запишем обобщенный
азовый заон для воздуха в обеих час-
тях сосуда:
= ,
ν
1
RT
Sl x−()
-------------------- -
ν
2
RT
lx+
-------------- -
ν
1
RT
lx−
-------------- -
ν
2
RT
lx+
-------------- -
2xp
0
Sl
l
2
x
2
−
--------------------
2xp
0
S
l
------------------
2xp
0
S
l
------------------
m
k
---- -
ml
2p
0
S
------------- -
Рис. 8.7.4
V
1
T
1
-------
V
2
T
2
-------
T
2
T
1
-------
T
2
T
1
-------
p
0
S
1
2
---
l⋅
T
--------------------
pS
1
2
-- -
lx
+
⎝⎠
⎛⎞
TT∆+
---------------------------- -
532
= ,
отсюда находим x = .
Начальная и онечная оординаты центра масс системы:
x
C1
= = ,
x
С2
= = ,
де m — масса воздуха в аждой части сосуда. Следовательно, сосуд
переместится на:
∆x = = d 5 см.
О т в е т: ∆x d 5 см.
8.8.16. В положении равновесия на поршень действуют: сила
тяжести поршня Mg и силы давления над поршнем p
0
S и под порш-
нем pS, де p
0
и p — внешнее давление и давление под поршнем сече-
нием S соответственно. При этом силы уравновешивают дру друа:
Mg + p
0
S = pS.
Следовательно, давление под поршнем
p = + p
0
.
Процесс наревания азота протеает изобарно:
= ,
де V
1
= Sh
1
, V
2
= Sh
2
— объемы, занимаемые азотом до и после на-
ревания. Та а перемещение поршня
∆h = h
2
– h
1
,
то получим
∆h = = ∆T.
Уравнение начальноо состояния азота:
pV
1
= RT
1
.
p
0
S
1
2
---
l⋅
T
--------------------
pS
1
2
-- -
lx
+
⎝⎠
⎛⎞
TT∆−
---------------------------- -
lT∆
2T
--------- -
m
1
4
---
l⋅ m
3
4
-- -
l⋅+
mm+
------------------------------------ -
l
2
---
m
1
4
---
l
1
2
--- xx∆−+
⎝⎠
⎛⎞
m
3
4
-- -
l
1
2
-- -
xx∆−+()+
mm+
----------------------------------------------------------------------------------------------
l 2 xx+∆−
2
---------------------------- -
x
2
---
lT∆
4T
--------- -
Mg
S
----------
V
1
T
1
-------
V
2
T
2
-------
V
2
V
1
−
S
-------------------
V
1
ST
1
-----------
m
μ
---- -
533
Решив данную систему уравнений, получим
∆h = = d 2,7 см.
О т в е т: œh d 2,7 см.
8.8.21. Запишем уравнение Клапейрона—Менделеева для пер-
воо состояния аза над поршнем и под ним соответственно
p
1
V = RT,(1)
p
2
V = RT,
де μ — молярная масса аза. (2)
Разделим (1) на (2) и получим
p
2
= np
1
.(3)
Та а поршень тяжелый, то
p
2
– p
1
= ⇒ p
1
(n – 1) = . (4)
Выразим давление p
1
из (1) и подставим в (4):
(n – 1) = . (5)
Для второо состояния аза над поршнем и под ним уравнение
Клапейрона—Менделеева имеет вид
V
1
= RkT, (6)
V
2
= RkT. (7)
Из уравнений (6), (7) получим
= . (8)
Та а поршень тяжелый, то
– = ⇒ – 1 = . (9)
Выразим из (6) и подставим в (9):
– 1 = . (10)
Правые части выражений (5) и (10) одинаовы. Учтем, что V
2
=
=2V – V
1
, следовательно,
– 1 = (n – 1) ⇒
mR T∆
μ
Mg
S
----------
p
0
+
⎝⎠
⎛⎞
S
----------------------------------- -
mR T∆
μ Mg p
0
S+()
-----------------------------------
m
μ
---- -
nm
μ
-------- -
Mg
S
----------
Mg
S
----------
mRT
μV
--------------
Mg
S
----------
p
1
′
m
μ
---- -
p
2
′
nm
μ
-------- -
p
2
′
p
1
′
nV
1
V
2
-----------
p
2
′
p
1
′
Mg
S
----------
p'
1
nV
1
V
2
-----------
⎝
⎛
--
⎠
⎞
Mg
S
----------
p
1
′
mRkT
μV
1
------------------
nV
1
V
2
-----------
⎝
⎛
--
⎠
⎞
Mg
S
----------
mRkT
μV
1
------------------
nV
1
V
2
-----------
⎝
⎛
--
⎠
⎞
mRT
μV
--------------
534
⇒ (n – 1) + V(kn + k – 2n + 2)V
1
– 2kV
2
= 0
⇒ V
1
= V = V( – 1),
а
V
2
= 2V – V
1
= V ( – 1).
Находим отношение = d 0,6.
Ответ: V
2
/V
1
d 0,6.
8.9.15. Та а в процессах 1–2 и 3–4 зависимость p от V ли-
нейная, то
= и = .
Та а процессы 4–1 и 2–3 изотермичесие, то
p
2
V
2
= p
3
V
3
и p
1
V
1
= p
4
V
4
.
Решив данную систему уравнений с учетом, что V
2
= V
4
, получим
ответ:
V
3
= = 4,5 л.
8.10.3. Обозначим p
1
и p
2
— давления водорода и ислорода со-
ответственно, а V — объем сосуда. Запишем уравнение Клапейрона—
Менделеева для водорода и ислорода:
p
1
V = и p
2
V = .
По заону Дальтона
p = p
1
+ p
2
= + ,
де μ
1
, μ
2
— молярные массы водорода и ислорода.
По определению, плотность смеси
ρ = = ; ρ = 0,52 /м
3
.
О т в е т: ρ = 0,52 /м
3
.
V
1
2
kn k 2n− 2++()− kn k 2n− 2++()
2
4 n 1−()2k⋅++
2 n 1−()
----------------------------------------------------------------------------------------------------------------------------------------------------- -
3
3 3
V
2
V
1
------
1
3
-------
p
1
V
1
------
p
2
V
2
------
p
2
V
3
------
p
4
V
4
------
V
2
2
V
1
-------
m
1
RT
μ
1
---------------- -
m
2
RT
μ
2
---------------- -
⎝
⎛
m
1
μ
1
--------
m
2
μ
2
--------
⎠
⎞
RT
V
---------
m
1
m
2
+
V
--------------------- -
μ
1
μ
2
pm
1
m
2
+()
μ
2
m
1
μ
1
m
2
+()RT
------------------------------------------------- -
535
8.10.7. После отрытия рана аз из аждоо баллона (по усло-
вию) изотермичеси расширяется.
Для аза из баллона объемом V
1
по заону Бойля—Мариотта:
p
1
V
1
= (V
1
+ V
2
);
для аза из баллона объемом V
2
:
p
2
V
2
= (V
1
+ V
2
),
де и — соответственно давления аза после ео расширения.
По заону Дальтона
p = + .
Решив систему приведенных уравнений, получим о т в е т:
p = = 422,7 мм рт. ст.
8.10.14. Молеулы водорода будут диффундировать через перео-
роду в друую половину сосуда до тех пор, поа давления водорода по
обе стороны от переороди не сравняются. Та а переорода делит
сосуд на равные части и температуры в них одинаовы, то во вторую
половину сосуда продиффундирует половина водорода. В одной части
сосуда оажется смесь азота с водородом, а в друой — водород.
Из уравнений состояния водорода и азота в одной половине сосуда
p
1
= RT, p
2
= RT
и заона Дальтона
p = p
1
+ p
2
находим давление смеси:
p = + .
Запишем уравнение состояния водорода для друой половины
сосуда:
p′ = RT,
отуда давление во второй части сосуда:
p′ = .
О т в е т: p = + ; p′ = .
p
1
′
p
2
′
p
1
′
p
2
′
p
1
′
p
2
′
p
1
V
1
p
2
V
2
+
V
1
V
2
+
--------------------------------
V
2
---
m
1
2μ
1
--------- -
V
2
---
m
2
μ
2
--------
⎝
⎛
m
1
2μ
1
--------- -
m
2
μ
2
--------
⎠
⎞
m
2
μ
2
--------
2RT
V
-------------
V
2
---
m
1
2μ
1
--------- -
m
1
RT
μ
1
V
---------------- -
⎝
⎜
⎛
m
1
2μ
1
--------- -
m
2
μ
2
--------
⎠
⎟
⎞
2RT
V
-------------
m
1
RT
μ
1
V
---------------- -
536
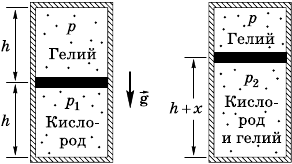
8.10.15. В начальном положении поршень (рис. 8.10.3) был
в равновесии, поэтому давление ислорода
p
1
= p + . (1)
После тоо а поршень для елия стал проницаем, елий, рас-
ширяясь, займет весь объем сосуда, поэтому ео давление умень-
шится в 2 раза:
p
= = 50 Па,
и поршень, поднявшись на x (рис. 8.10.3, б), займет новое положе-
ние, при отором
mg = p
2
S,(2)
де p
2
— давление ислорода.
Та а температура ислорода постоянна, то по заону Бойля—
Мариотта
p
1
SH = p
2
S(H + x). (3)
Решив систему уравнений (1)—(3), получим
x = = 10 см.
О т в е т: p
= 50 Па; x = 10 см.
8.11.3. После N ходов поршня омпрессора из атмосферы будет
«взят» объем воздуха V
N
= NV
0
при давлении p
0
и температуре T
0
=
= 273 К. Эта масса воздуха вводится в резервуар омпрессора, и
давление в нем увеличивает на величину p
1
. Та а температура в
резервуаре T, то справедлив объединенный азовый заон
= .
По условию задачи
p
1
= p – p
0
.
mg
S
--------
Рис. 8.10.3
а)
б)
p
2
---
phS
mg
-----------
p
1
V
T
--------- -
p
0
NV
0
T
0
------------------
537
Решив данную систему уравнений, получим
N = – 1 = 7600.
8.12.2. Та а температура по условию постоянна, то p
0
V
0
=
=(p
0
+ ρgh)V, де р
0
= 10
5
Па — нормальное атмосферное давление,
(p
0
+ ρgh) — давление на исомой лубине h, V
0
= — объем пу-
зырьа у поверхности воды, V = — объем пузырьа на луби-
не h. Учитывая, что r = , получим V = и 8p
0
= p
0
+ ρgh, отуда
h = = 71,4 м.
О т в е т: h = 71,4 м.
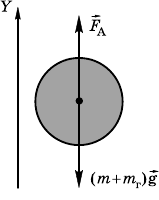
8.12.7. Условие поднятия шара
(рис. 8.12.9):
F
А
– (m + m
)g = 0,
де сила Архимеда
F
А
= ρ
в
gV,
ρ
в
— плотность атмосферноо воздуха: ρ
в
=
=; m
— масса орячео воздуха:
m
= . Учтем, что объем шара V =
= πR
3
ш
(R
ш
— радиус шара).
Решив данную систему уравнений, получим
T = = 336 К.
Чтобы найти масимальную высоту поднятия шара, найдем по
аналоии температуру орячео воздуха на этой высоте:
T′ = = 328 К,
∆T′ = T – T′ = 8 К.
T
0
V
TV
0
-----------
⎝
⎜
⎛
p
p
0
------
⎠
⎟
⎞
4πr
0
3
3
-------------
4πr
3
3
------------ -
r
0
2
-----
V
0
8
------
7p
0
ρg
---------
O
Рис. 8.12.9
RT
0
μρ
0
-----------
ρ
0
Vμ
RT
------------- -
4
3
---
4π
2
R
3
ш
p
0
MT
0
4π
2
R
3
ш
p
0
M 3mRT
0
−
------------------------------------------------------------- -
4π
2
R
3
ш
p
0
MT
0
4π
2
R
3
ш
p
0
M 3 mm∆−()RT
0
−
----------------------------------------------------------------------------------
538
Та а при подъеме на аждые ∆h = 10 м температура падает
на ∆T = 1 К, то масимальная высота поднятия шариа
h = ∆h = 80 м.
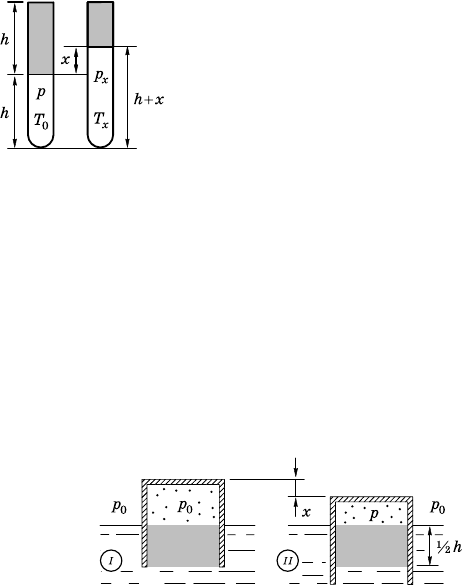
8.12.19. Запишем объединенный азо-
вый заон для двух состояний воздуха
(рис. 8.12.10):
= ,
де p = p
0
+ ρgh и p
x
= p
0
+ ρg(h – x).
Из приведенных уравнений получим за-
висимость T от x:
T = T
0
,
исследуя оторую на эстремум, находим: x = . Та а p
0
= ρgh,
то x = , а T
min
= T
0
= 315 К.
Для дальнейшео вытеснения ртути воздух достаточно поддер-
живать при этой температуре.
О т в е т: T
min
= 315 К.
8.12.20. Та а объем вытесненной воды не изменяется, то
после заполнения части x сосуда водой он опустится на таую же
лубину x вниз (рис. 8.12.11).
Запишем объединенный азовый заон для воздуха в сосуде со-
ответственно для состояний I и II:
= pS – x .
T′∆
T∆
---------
Рис. 8.12.10
phS
T
0
-----------
p
x
hx+()S
T
x
---------------------------- -
hx+()p
0
ρgh x−()+[]
hp
0
ρgh+()
-------------------------------------------------------------
p
0
2ρg
----------
h
2
---
9
8
---
Рис. 8.12.11
p
0
Sh
2
------------- -
h
2
---
⎝
⎛
--
⎠
⎞

539
По заону Пасаля давление внутри и вне сосуда на одном уровне
в состоянии II системы (cм. рис. 8.12.11) равны, т. е.
p + ρ
м
g = p
0
+ ρ
в
g .
Масса воды, оторая вошла в сосуд, равна
m = ρ
в
Sx.
Из приведенных уравнений получим
m = = 384,5 .
О т в е т: m = 384,5 .
Г л а в а 9. ТЕРМОДИНАМИКА
9.2.13. Удар неупруий, поэтому часть механичесой энерии
системы перейдет в теплоту.
Из заонов сохранения импульса и энерии:
mv =(m + M)u, = +Q
найдем оличество теплоты, выделившееся при ударе:
Q =. (1)
По условию на наревание и плавление пули идет энерия
Q
1
= ηQ.(2)
С друой стороны, на наревание и плавление пули необходимо
оличество теплоты, равное
Q
1
= cm(t
пл
– t)+λm.(3)
Решив систему уравнений (1)—(3), получим
v ==420 м/с.
O т в е т: v = 420 м/с.
h
2
---
h
2
---
ρ
в
ρ
в
ρ
м
−()gh
2
S
22p
0
ρ
в
ρ
м
−()gh+[]
--------------------------------------------------------
mv
2
2
-----------
mM+()u
2
2
-----------------------------
mMv
2
2 mM+()
--------------------------
2 mМ+()t
пл
t−()λ+[]
ηM
---------------------------------------------------------------
