Турчина Н.В. Физика в задачах для поступающих в вузы
Подождите немного. Документ загружается.

410
Пути, проходимые за ∆t = 1 с при равноусоренном движении,
если начальная сорость равна нулю, относятся, а нечетный ряд
натуральных чисел: ∆s
1
: ∆s
2
: ∆s
3
: ∆s
4
... = 1 : 3 : 5 : 7 ... .
О т в е т: œs
1
: œs
2
: œs
3
: œs
4
... = 1 : 3 : 5 : 7... .
1.4.12. Путь s
1
, проходимый за время t
1
:
s
1
= v
0
t +.
Путь s
1
+ s
2
, проходимый за время t
1
+ t
2
:
s
1
+ s
2
= v
0
(t
1
+ t
2
)+ .
Решив систему приведенных уравнений, получим
a = = 0,07 м/с
2
.
О т в е т: a = 0,07 м/с
2
.
1.4.13. Первую часть пути, пройденноо точой, выразим соот-
ношением
l
1
=,
де а — усорение точи, а последнюю часть пути —
l
2
= v
1
t
2
+.
Время, в течение отороо точа приобрела сорость v
1
:
t
3
=.
Время движения точи на всем пути равно
t
0
= t
3
+ t
2
.
Путь, пройденный точой,
s =.
Решив систему приведенных уравнений, получим
s =; s = 612,5 м.
О т в е т: s = 612,5 м.
at
1
2
2
---------
at
1
t
2
+()
2
2
--------------------------- -
2 s
2
t
1
s
1
t
2
−()
t
1
t
2
t
1
t
2
+()
-------------------------------------
at
1
2
2
---------
at
2
2
2
---------
v
1
a
------
at
0
2
2
---------
l
1
t
1
2
---- -
l
2
t
1
2
l
1
t
2
2
+
2l
1
t
2
-------------------------- -
⎝⎠
⎜⎟
⎛⎞
2

411
1.4.14. Пусть l — длина одноо ваона: l =, де а — усорение
элетричи. Мимо пассажира пройдут пять ваонов за время t
5
,
следовательно, можем записать 5l = , отуда находим t
5
= t
1
.
Четыре ваона пройдут за время
t
4
= t
1
=2t
1
.
Шестой ваон (для пассажира — пятый) пройдет за время
t
2
= t
5
– t
4
= t
1
(–2); t
2
d 1,2 c.
О т в е т: t
2
d 1,2 с.
1.4.15. Пусть l— длина одноо ваона, v
0
— сорость элет-
ричи моменту, ода последний ваон начинает проезжать мимо
человеа на перроне, ∆t — время отставания часов.
Путь, пройденный предпоследним ваоном,
l = v
0
t
1
+,
а двумя последними ваонами —
2l=v
0
(t
1
+ t
2
)+ .
Сорость элетричи
v
0
= a∆t.
Решив систему приведенных уравнений, получим
∆t =; ∆t d 31 с.
Ответ: на œt d 31 с.
1.4.16. 1. Харатер движения лифта менялся дважды, следо-
вательно, движение лифта нужно рассматривать на трех участах.
На первом участе лифт двиался равноусоренно, и высота ео
поднятия
h
1
=<v
1
> t
1
, (1)
де <v
1
> — средняя сорость на этом участе.
Та а движение равноусоренное, то <v
1
>= =
= = . Учитывая это, перепишем уравнение (1): h
1
=.
На втором участе лифт двиался равномерно, поэтому высота
ео поднятия h
2
= vt
2
, а на третьем участе он двиался замедленно
at
1
2
2
---------
at
5
2
2
---------
5
4
5
at
1
2
2
---------
at
1
t
2
+()
2
2
--------------------------- -
t
2
2
2t
1
t
2
t
1
2
−+
2 t
1
t
2
−()
-------------------------------------
v
нач
v
он
+
2
----------------------------
0 v+
2
-------------
v
2
---
vt
1
2
--------
412
до полной останови; следовательно, можно по аналоии приме-
нить формулу h
3
= . Поэтому вся высота
h = h
1
+ h
2
+ h
3
=+vt
2
+=v + t
2
+;
h = 4 + 8 + м = 4(2 + 8 + 1,5) м = 46 м.
Средняя сорость движения: <v>= , <v>=3м/с.
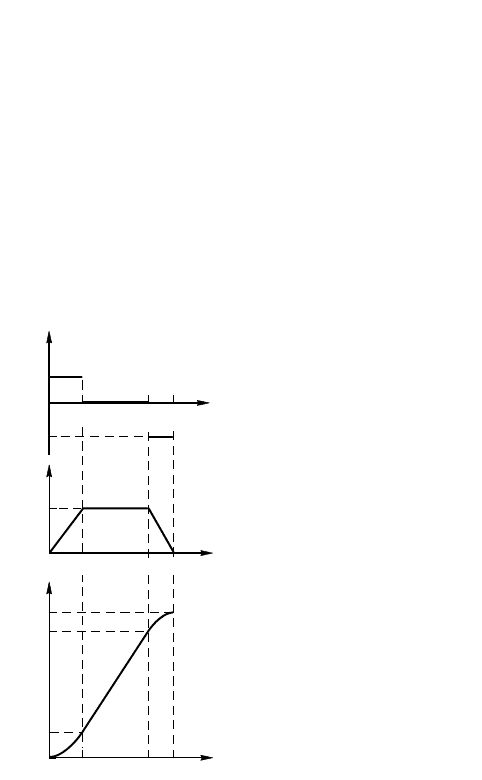
2. Построим рафии усорения, сорости и перемещения
лифта, рассматривая аждый участо отдельно. Графи усорения
поазан на рис. 1.4.6, а.
В интервале времени 0 < t < 4 с усорение a
1
=1м/с
2
; в интер-
вале времени 4 с < t <12с усорение a
2
= 0, та а движение равно-
мерное; в интервале времени 12 с < t <15с усорение a
3
=–1,3м/с
2
.
Графи сорости поазан на рис. 1.4.6, б.
В интервале времени 0 < t < 4 с сорость лифта равномерно рас-
тет от 0 до 4 м/с; в интервале времени 4 с < t < 12 с сорость лифта
постоянна и равна 4 м/с; в интервале
времени 12 с < t < 15 с сорость лифта
равномерно уменьшается от 4 м/c до 0.
Графи перемещения поазан на
рис. 1.4.6, в.
В интервале времени 0 < t <4с пере-
мещение изменяется по заону ∆y
1
=
= = .
Перемещение на этом участе дви-
жения: h
1
= 8 м.
В интервале времени 4 с < t <12с
перемещение увеличивается линейно:
∆y
2
= v ∆t =4(t –4)=4t –16.
Перемещение на втором участе:
h
2
=32м.
В интервале времени 12 с < t <15с
перемещение изменяется по заону:
∆y
3
= v∆t + = 4(t – 1 2) –
– = –+14t –140.
vt
3
2
--------
vt
1
2
--------
vt
3
2
--------
⎝
⎛
t
1
2
---- -
t
3
2
---- -
⎠
⎞
⎝
⎛
4
2
---
3
2
---
⎠
⎞
h
t
1
t
2
t
3
++
--------------------------- -
a,
м/с
2
t, с
0
4
–1,3
v,
м/с
t, с
t, с
Δ y, м
0
0
12 15
1
а)
б)
в)
4
12 15
4
12 15
46
40
8
4
Рис. 1.4.6
a
1
t
2
2
------------
t
2
2
---- -
a
3
∆t
2
2
----------------
1,3 t 12−()
2
2
--------------------------------
2t
2
3
-------- -

413
Перемещение на третьем участе: h
3
=6м.
Ответ: 1) h = 46 м, <v> = 3 м/с; 2) рис 1.4.6, а, 1.4.6, б, 1.4.4, в.
1.4.18. Расстояние от Земли до звезды:
s=2s
1
+ s
2
,
де s
1
— путь звездолета при разоне, равный пути торможения;
s
1
= (t
1
— время разона или торможения); s
2
— путь при рав-
номерном движении:
s
2
= v –2t
1
,
де v — сорость равномерноо движения, равная онечной (на-
чальной) сорости разона (торможения),
v
1
= at
1
.
Решив систему приведенных уравнений, найдем усорение
звездолета:
a =.
Усорение будет минимальным, если знаменатель y = t
1
t –
будет масимальным. Найдем t
1
, при отором знаменатель маси-
мален: t
1
= – = . Следовательно, минимальное усорение
a
min
==0,2м/с
2
.
О т в е т: a
min
= 0,2 м/с
2
.
1.4.19. 1-й с п о с о б. Сравним данное уравнение движения с урав-
нением движения в общем виде:
x = x
0
+ v
x0
t +; x =15t +0,4t
2
. (1)
Очевидно, что x
0
=0; v
x0
=15м/с; =0,4м/с
2
, отуда a
x
=
=0,8м/с
2
.
Координату тела через 5 с найдем из уравнения (1):
x = (15 · 5 + 0,4 · 5
2
) м = 85 м.
at
1
2
2
---------
⎝
⎛
t
2
---
⎠
⎞
2s
t
1
t 2t
1
−()
----------------------------
2t
1
2
b
2a
------ -
t
4
---
10s
t
2
--------- -
a
x
t
2
2
----------- -
a
x
2
----- -

414
Сорость тела в момент времени 5 с определим по формуле:
v
x
= v
x0
+ a
x
t; v
x
= 19 м/с. Средняя сорость за данное время:
v =; v =17м/с,
а путь
s = v
0
t +=85м.
В данной задаче оордината, перемещение и путь одинаовы.
2-й с п о с о б. Координату найдем из уравнения (1). По опреде-
лению, сорость: v
x
= xR = (15t +0,4t
2
)R =15+0,8t; v
x
=19м/с.
Усорение: a
x
=(v
x
)R =(15+0,8t)R = 0,8 м/с
2
.
Ответ: а) x
0
= 0, v
x0
= 15 м/с; б) x = 85 м, v
x
= 19 м/с; в) v=17 м/с,
s = 85 м.
1.4.20. Точа начинает движение в момент времени t
0
=0 из
оординаты x
0
= 5 м в положительном направлении оси OX с на-
чальной соростью v
0x
= 4 м/с и усорением a
x
=–4м/с
2
. Опреде-
лим, существует ли в данном интервале времени движения момент
времени, в оторый изменяется направление движения точи. Для
этоо найдем момент времени, ода сорость точи равна нулю.
Сорость точи изменяется по заону: v
x
=4–4t, поэтому
0=4–4t
поворота
⇒ t
поворота
=1с.
1)
Следовательно, в интервале вре-
мени 0 m t m 1 с точа движется в положительном направлении оси
OX, а в интервале времени 1 с m t m 3 с возвращается началу оор-
динат. Найдем оординату поворота точи:
x
поворота
=5+4t
поворота
–2t
2
поворота
=(5+4–2)м=7м.
Тода путь, пройденный точой при движении в положитель-
ном направлении оси OX,
s
1
= x
поворота
– x
0
=(7–5) м=2м.
Конечная оордината движения точи:
x =(5+4·3–2·3
2
) м = –1 м.
Путь, пройденный точой при движении началу оординат,
s
2
= x
поворота
– x
0
= (7 – (–1)) м = 8 м,
а весь путь
s = s
1
+ s
2
=(2+8)м=10м.
О т в е т: s = 10 м.
1)
В решениях данноо сборниа часто используется зна ⇒, оторый
заменяет слово «отуда».
v
x
v
x0
+
2
---------------------
at
2
2
---------
415
1.5.9. В момент отрыва сосульи от рыши ее начальная со-
рость равна нулю. Кода сосульа подлетела верхнему раю она,
у нее была сорость v. Данную сорость находим из соотношения
h = vt + g ; v =– . (1)
Высоту относительно верхнео рая она определим из соотно-
шения H = , подставив в нео выражение (1):
H = – =2,17м.
О т в е т: H = 2,17 м.
1.5.11. Направим ось OY вертиально вверх, совместив начало
оординат с точой бросания. Тело на заданной высоте будет
находиться дважды: при движении вверх и при движении вниз. Ес-
ли обозначить данные моменты времени соответственно t
1
и t
2
, то
тело будет находиться на высоте, большей h = 14,7 м, в течение вре-
мени
∆t = t
2
– t
1
.(1)
Запишем заон движения тела в выбранной системе отсчета:
y = v
0
t–g . В моменты времени t
1
и t
2
оордината y = h, поэтому
h = v
0
t – g или
gt
2
–2v
0
t +2h = 0. (2)
Корни вадратноо уравнения (2) и есть моменты времени t
1
и t
2
:
t
1,2
=, т.е.
t
1
=, (3)
t
2
=. (4)
Подставим выражения (3), (4) в (1) и получим ∆t = = 2 с.
О т в е т: œt = 2 с.
t
2
2
---- -
h
t
---
gt
2
------
v
2
2g
------ -
1
2g
------ -
⎝
⎛
h
t
---
gt
2
------
-
⎠
⎞
2
t
2
2
---- -
t
2
2
---- -
v
0
v
0
2
2gh−±
g
--------------------------------------- -
v
0
v
0
2
2gh−−
g
--------------------------------------- -
v
0
v
0
2
2gh−+
g
--------------------------------------- -
2 v
0
2
2gh−
g
-------------------------------

416
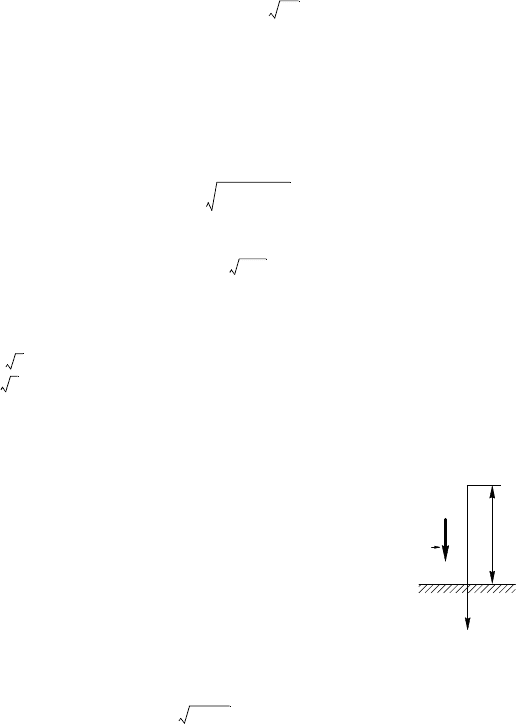
1.5.12. Направим ось Y вертиально вверх, начало
оси — точу O — поместим на поверхности земли
(рис. 1.5.1). Запишем заон движения мяча в
выбранной системе отсчета:
y = vt –. (1)
Кода мяч достиает высоты h (это происходит дваж-
ды), то уравнение (1) принимает вид
h = vt
1
–(2)
и
h = vt
2
–, (3)
де по условию
t
2
= t
1
+ ∆t. (4)
Решив совместно уравнения (2)—(4), получим
v =; v = 20 м/с.
Масимальная высота подъема h
max
= = 20 м.
О т в е т: v = 20 м/с; h
max
= 20 м.
1.5.13. Направим ось OY вертиально вверх, тода проеция
сорости на ось OY изменяется по заону v = v
0
– gt. При движении
вверх проеция сорости положительна, поэтому = v
0
– gt
1
,
отуда находим t
1
= = 1 с. При движении вниз проеция
сорости отрицательна, поэтому = v
0
– gt
2
и тода t
2
= =
= 3 с.
(При расчетах принято g =9,8м/с
2
, та а число 19,6 рат-
но 9,8.)
О т в е т: t
1
= 1 c; t
2
= 3 c.
1.5.17. Сорость падения первоо шариа на землю найдем из
соотношения
h =; v =, (1)
v
g
Y
h
0
Рис. 1.5.1
gt
2
2
---------
gt
1
2
2
--------
gt
2
2
2
--------
2gh g
2
t
2
+
4
---------------------------------
v
2
2g
------ -
v
0
n
------
v
0
n 1−()
ng
------------------------
v
0
n
------
v
0
n 1+()
ng
------------------------
v
2
2g
------ -
2gh
417
а сорость второо шариа перед падением на пластину — из
соотношения
=; v
1
=. (2)
После пробивания пластини сорость шариа станет в 2 раза
меньше, т. е.
v
01
=, (3)
и он пролетит следующую половину пути: = , отуда
v
2
=. (4)
Подставим в (4) выражения (2), (3) и получим
v
2
=. (5)
Разделим выражение (1) на (5) и найдем, что в момент падения
на землю сорость первоо шариа больше сорости второо в
= = 1,26 раза.
О т в е т: = 1,26.
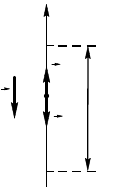
1.5.18. Тело отсчета — Земля. Направим ось Y
вниз, начало оси поместим в точе сброса руза
(рис. 1.5.2).
a) Если вертолет неподвижен, то заон движения
руза:
y =. (1)
Кода руз достинет земли (y = h, t = t
1
), уравне-
ние (1) примет вид: h = , отуда время падения
руза на землю:
t
1
=; t
1
= 7,8 с.
б) Если вертолет опусается со соростью v, то у руза относитель-
но земли будет начальная сорость v, поэтому заон движения руза:
y = vt + .(2)
h
2
---
v
1
2
2g
------ -
gh
v
1
2
------
h
2
---
v
2
2
v
01
2
−
2g
---------------------
v
01
2
2gh+
5gh
2
-------------- -
v
v
2
------
22
5
-----------
v
1
v
2
------
g
0
Y
h
Рис. 1.5.2
gt
2
2
---------
gt
1
2
2
--------
2hg⁄
gt
2
2
---------

418
Кода руз достинет земли (y = h, t = t
2
), уравнение (2) примет вид:
h = vt
2
+ , отуда
+2vt
2
–2h =0.
Решив полученное уравнение, находим
t
2
=.
Следовательно, t
2
= 7,3 с (отрицательный орень в данной зада-
че физичесоо смысла не имеет, та а t >0).
в) Если вертолет поднимается со соростью v, то у руза относи-
тельно земли будет начальная сорость v (направлена вверх), поэто-
му заон движения руза:
y =–vt +. (3)
Кода руз достинет земли (y = h, t = t
3
), уравнение (3) примет
вид: h =–vt
3
+ , отуда
gt
3
2
–2vt
3
–2h =0.
Решив полученное уравнение, находим
t
3
=.
Следовательно, t
3
= 8,3 с (отрицательный орень в данной зада-
че физичесоо смысла не имеет, та а t>0).
Ответ: а) t
1
= 7,8 с; б) t
2
= 7,3 с; в) t
3
= 8,3 с.
1.5.23. В момент отрыва десятой апли первая будет находиться
в полете в течение времени t
1
=9τ и пролетит расстояние
h
1
= g = g ,(1)
а четвертая апля будет в полете в течение времени t
2
=6τ и проле-
тит расстояние
h
2
= g = g .(2)
Расстояние между первой и четвертой аплями в момент отры-
ва десятой
s = h
1
– h
2
.(3)
gt
2
2
2
--------
gt
2
2
v− v
2
2gh+±
g
----------------------------------------
gt
2
2
---------
gt
3
2
2
--------
v v
2
2gh+±
g
-------------------------------------
t
1
2
2
---- -
81τ
2
2
------------
t
2
2
2
---- -
36τ
2
2
------------
419
Подставим в (3) выражения (1) и (2) и получим s = g ; s =9м.
В момент отрыва десятой апли сорость первой v
1
= gt
1
=9gτ,
четвертой v
2
= gt
2
=6gτ. Сорость движения первой апли относи-
тельно четвертой v = v
1
– v
2
=
3gτ; v =6м/с.
О т в е т: s = 9 м; v = 6 м/с.
1.5.27. Тело отсчета— Земля. Направим ось Y
вертиально вверх, начало оси совместим с точой O,
в оторой находится шар в момент времени t
0
=0 —
момент бросания руза (рис. 1.5.3). Тода заон
движения шара:
y
1
=–vt. (1)
По условию задачи сорость руза дана отно-
сительно шара. Найдем проецию начальной со-
рости руза на данную ось относительно земли:
u
отн
= u – v.
Заон движения руза:
y
2
= u
отн
t –=(u – v)t– .(2)
Расстояние между рузом и шаром в любой момент времени
равно
∆y = y
2
– y
1
.(3)
В наивысшей точе подъема руз будет находиться в момент
времени
t
1
==, (4)
это время шар опусался. Решив систему уравнений (1)—(4), най-
дем расстояние между рузом и шаром в момент t
1
:
∆y
1
=(u – v)t
1
––(–vt
1
)= ; ∆y
1
=19,2м.
В момент времени t
2
, ода руз будет находиться рядом с ша-
ром, оординаты тел будут одинаовы: y
2
= y
1
, или с учетом урав-
нений (1) и (2):
(u – v)t
2
–=–vt
2
,
отуда
t
2
= = 4 с.
О т в е т: œy
1
= 19,2 м; t
2
= 4 с.
45τ
2
2
------------
u
отн
g
v
y
1
y
2
Y
Δ y
O
Рис. 1.5.3
gt
2
2
---------
gt
2
2
---------
u
отн
g
---------- -
uv−
g
-------------
gt
1
2
2
--------
u
2
v
2
−
2g
------------------
gt
2
2
2
--------
2u
g
------ -
