Толпаев В.А. Математические модели двумерной фильтрации в анизотропных, неоднородных и многослойных средах
Подождите немного. Документ загружается.


310
найдены, то, как известно
1
, уравнения самих цилиндрических поверхностей
будут определяться как поверхности уровня функций
−−=
−−=
n
mz
y
n
lz
xqq
n
mz
y
n
lz
xpp
,
,
0
0
. (1)
Первые два ГНА, как следует из (1), будут задаваться векторами
p
p
h
∇
∇
=
1
r
и
q
q
h
∇
∇
=
2
r
, где k
n
m
v
p
n
l
u
p
j
v
p
i
u
p
p
r
rr
⋅
∂
∂
+⋅
∂
∂
−
∂
∂
+
∂
∂
=∇
0000
; (2)
k
n
m
v
q
n
l
u
q
j
v
q
i
u
q
q
r
rr
⋅
∂
∂
+⋅
∂
∂
−
∂
∂
+
∂
∂
=∇
0000
; (3)
n
mz
yv
n
lz
xu −=−= , . (4)
Для того чтобы векторы
1
h
r
и
2
h
r
удовлетворяли условию ортогональности,
потребуем выполнение равенства
0),(
=
∇
∇
qp . В развернутой форме записи
оно принимает вид
0
00000000
=
⋅
∂
∂
+⋅
∂
∂
⋅
∂
∂
+⋅
∂
∂
+
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
n
m
v
q
n
l
u
q
n
m
v
p
n
l
u
p
v
q
v
p
u
q
u
p
, или,
что одно и то же,
011
00
2
2
2
000
22
2
0
=
∂
∂
∂
∂
++⋅
∂
∂
+
∂
∂
∂
∂
⋅+
+
∂
∂
v
q
v
p
n
m
n
lm
u
p
u
q
v
p
n
lm
n
l
u
p
. Если
последнее равенство переписать в виде пропорции
),(
11
0
0
2
2
2
0
0
0
22
2
0
vuH
u
q
v
p
n
m
n
lm
u
p
v
q
v
p
n
lm
n
l
u
p
=
∂
∂
∂
∂
++⋅
∂
∂
−=
∂
∂
∂
∂
⋅+
+
∂
∂
, и общее частное двух
дробей обозначить как некоторую безразмерную непрерывную не равную
нулю функцию
),( vuH , то относительно функций ),(
0
vup и ),(
0
vuq получим
следующую систему дифференциальных уравнений
∂
∂
⋅−=
∂
∂
++
∂
∂
⋅
∂
∂
=
∂
∂
⋅+
∂
∂
+
u
q
vuH
v
p
n
m
u
p
n
lm
v
q
vuH
v
p
n
lm
u
p
n
l
00
2
2
0
2
00
2
0
2
2
),(1
;),(1
. (5)
1
Сборник задач по математике для втузов. 1 том. /Под ред. Ефимова А..В. и Демидовича Б.П./- М., Наука,
1981.

311
В соответствии с формулами (4) промежуточные переменные u и v при 0
=
z
равны соответственно
x
и y . Поэтому система уравнений (5) определяет
уравнения
),(
00
yxpp = и ),(
00
yxqq
=
семейств направляющих (в плоскости
xOy ) кривых для рассматриваемых цилиндрических поверхностей:
∂
∂
⋅−=
∂
∂
++
∂
∂
⋅
∂
∂
⋅=
∂
∂
⋅+
∂
∂
+
x
q
yxH
y
p
n
m
x
p
n
lm
y
q
yxH
y
p
n
lm
x
p
n
l
00
2
2
0
2
00
2
0
2
2
),(1
;),(1
. (5′)
С помощью любого частного решения
),(),,(
0000
yxqqyxpp =
=
системы
уравнений (5′), по формулам (1) будут задаваться ортогональные друг к
другу семейства цилиндрических поверхностей
constzyxp =),,( и
constzyxq =),,( , образующие которых параллельны вектору },,{ nmls =
r
. Третье
семейство поверхностей, ортогональное цилиндрическим поверхностям, как
уже сказано, представляет собой семейство параллельных между собой
плоскостей
constzyxr =),,( , где
nzmylxsRzyxr ++== ),(),,(
r
r
. (6)
Для того чтобы вычислить компоненты тензора проницаемости пористой
среды с рассматриваемыми законами распределения ГНА требуется
предварительно вычислить координаты векторов
321
,, hhh
r
r
r
, задающих поле
ГНА. Эти векторы направлены по градиентам функций
),,(),,,( zyxqzyxp и
),,( zyxr соответственно. С учетом формул (2), (3), (5’) и (6) получаем:
(
)
[
]
;
1
0000
1
1
kmplpjnpinp
D
p
p
h
yxyx
r
r
r
r
+−+=
∇
∇
= (7)
(
)
[
]
;
1
0000
2
2
kmqlqjnqinq
D
q
q
h
yxyx
r
r
r
r
+−+=
∇
∇
= (8)
knjmils
r
r
h
r
r
r
r
r
++==
∇
∇
=
3
, (9)
где
,
,)(2)(
,)(2)(
2
0
22
00
2
0
22
2
2
0
22
00
2
0
22
1
++++=
++++=
yyxx
yyxx
qnmqlmqqnlD
pnmplmppnlD
(10)
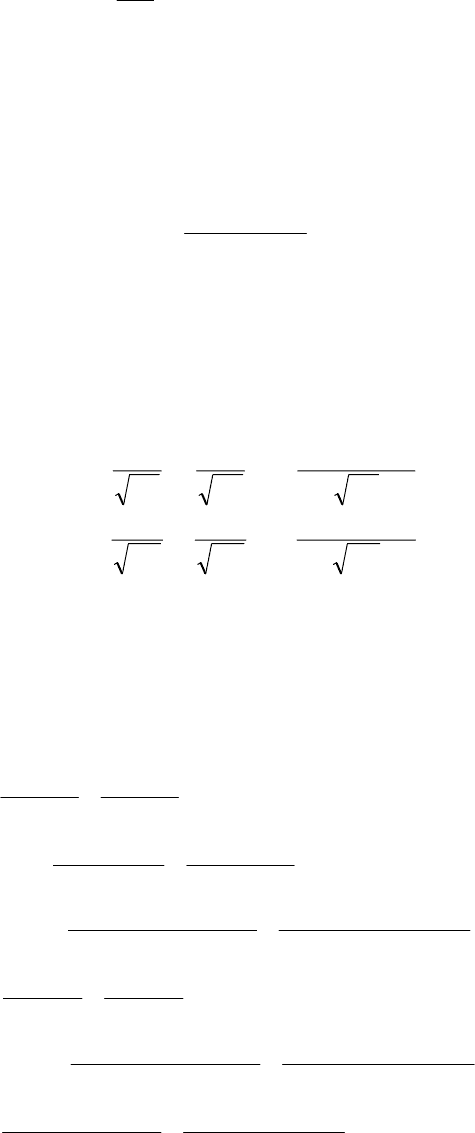
312
а через
x
p
0
обозначено
x
p
p
x
∂
∂
=
0
0
и т.д. С учетом того, что функции ),(
0
yxp и
),(
0
yxq связаны друг с другом системой уравнений (5’), между
коэффициентами
1
D и
2
D есть взаимозависимость, выражаемая, как легко
проверить, формулой
.
),(
22
1
2
yxHn
D
D
⋅
=
(11)
Далее, для расчета тензора проницаемости в декартовых координатах,
вычисляем матрицу перехода от базиса ГНА к базису
),,( kji
r
r
r
. Эта матрица П
имеет вид (П1.1.11). С помощью формул (7), (8) и (9) найдем, что
+
−
+
−
=
n;m;l
D
mqlq
;
D
nq
;
D
nq
D
mplp
;
D
np
;
D
np
П
2
y0x0
2
y0
2
x0
1
y0x0
1
y0
1
x0
. (12)
Наконец, по формуле (П1.3.6), в которой
K
′
имеет диагональный вид, а П
подставляем из (12), получим:
+
+
+
+
=
+
+
−
+
−==
++=
⋅+
+
−
+
−==
++==
++=
2
3
2
2
002
1
2
001
33
3
2
0002
1
0001
3223
2
3
2
2
0
2
2
1
2
0
2
1
22
3
2
0002
1
0001
3113
3
2
00
2
2
1
00
2
1
2112
2
3
2
2
0
2
2
1
2
0
2
1
11
)()(
)()(
)()(
n
D
mqlq
D
mplp
k
mn
D
mqlqnq
D
mplpnp
kk
m
D
qn
D
pn
k
nl
D
mqlqnq
D
mplpnp
kk
lm
D
qqn
D
ppn
kk
l
D
qn
D
pn
k
yxyx
yxyyxy
yy
yxxyxx
yxyx
xx
λ
λλ
λ
λλ
λ
λλ
λ
λλ
λ
λλ
λ
λλ
. (13)
Формулы (13), с учетом системы уравнений (5’) и формулы (11), можно
переписать в виде, содержащем лишь одну из функций
),(
0
yxp (или ),(
0
yxq ).
В частности, исключив с помощью (5’) функцию
),(
0
yxq , для компонент
тензора проницаемости в средах с цилиндрическими законами распределения
ГНА получим выражения:

313
[]
[]
[]
[]
[]
[]
,
.)()(
1
;)()(
1
;
1
;)()(
1
;
1
;
1
2
3
2
00
2
2
2
001
1
33
30020001
1
3223
2
3
2
2
2
0
2
1
1
22
30020001
1
3113
3200
2
1
1
2112
2
3
2
2
2
0
2
1
1
11
+−++=
+−++−==
++=
⋅+−++−==
+−==
++=
nmplpnmplp
D
k
mnmplpnbmplpnp
D
kk
mbpn
D
k
nlalpmpnmplpnp
D
kk
lmabppn
D
kk
lapn
D
k
xyyx
xyyxy
y
yxyxx
yx
x
λλλ
λλλ
λλλ
λλλ
λλλ
λλλ
(14)
где ради краткости записи обозначено:
.)(
;)(
00
22
0
22
0
yx
yx
lmppnlb
pmnlmpa
++=
++=
Из рассмотренных законов распределения ГНА выделим важный
частный случай, когда образующие цилиндрических поверхностей
cons
t
p
=
и
cons
t
q
= параллельны одной из координатных осей (к примеру, оси Oz ).
П2.4.2 Случай совпадения одного из ГНА цилиндрических законов с
координатной осью (осью
Oz )
Итак, пусть семейства двух взаимно ортогональных цилиндрических
поверхностей имеют образующие, параллельные оси
Oz . В этом случае
цилиндрические поверхности, как хорошо известно, задаются уравнениями
вида
constyxp =),( и constyxq =),( . Направляющий же вектор s
r
образующих
этих поверхностей совпадет с ортом оси
Oz и, поэтому, ),,( 100== ks
r
r
. Система
уравнений (5') с указанным вектором
s
r
для функций ),( yxp и ),(
y
xq в
декартовых координатах примет вид
x
q
yxH
y
p
y
q
yxH
x
p
∂
∂
⋅−=
∂
∂
∂
∂
⋅=
∂
∂
),(;),( , (15)
в которой
),( yxH - непрерывная положительная в области, занятой
анизотропной средой, функция. В качестве расчетной системы выберем
некоторую ортогональную криволинейную систему координат
),,( z
η
ξ
,
связанную с декартовыми равенствами
zzyx
y
x =
=
=
),,(),,(
η
η
ξ
ξ
. Так как
ξ
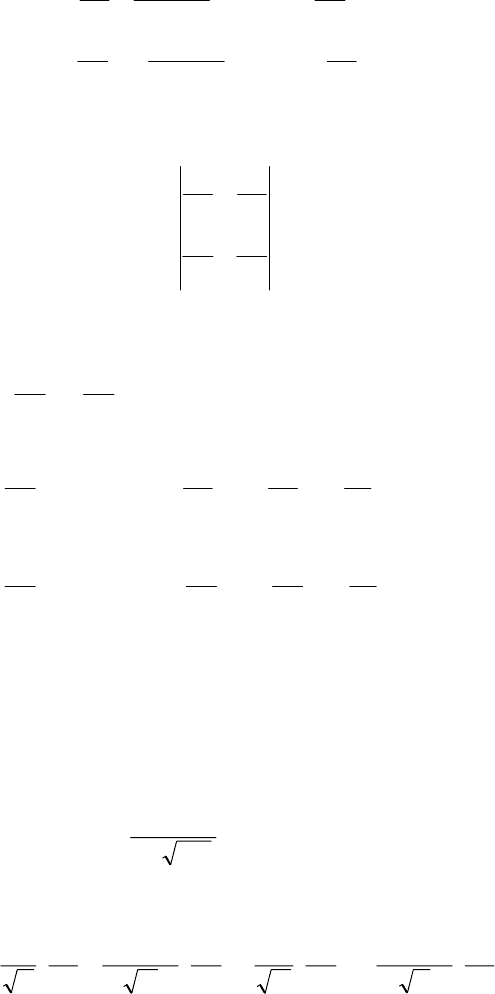
314
и
η
считаются ортогональными, то 0
=
∇
∇
),(
η
ξ
. Переходя в (15) к новым
переменным
ξ
и
η
, получим
∂
∂
∇∇⋅
∆
−=
∂
∂
∂
∂
∇∇⋅
∆
=
∂
∂
ξ
ξξ
ηξ
η
η
ηη
ηξ
ξ
q
H
p
q
H
p
),(
),(
,),(
),(
, (16)
где
yx
yx
∂
∂
∂
∂
∂
∂
∂
∂
=∆
ηη
ξ
ξ
. (17)
С целью упрощения записи системы уравнений (16) отметим, что скалярные
квадраты векторов
ξ
∂
∂
R
r
и
η
∂
∂
R
r
равны следующим выражениям:
);,(),(
ηη
ξξ
ηξ
ξ
∇∇⋅
∆
=
∂
∂
+
∂
∂
==
∂
∂
2
22
2
1
y
x
E
R
r
(18)
).,(),(
ξξ
ηη
ηξ
η
∇∇⋅
∆
=
∂
∂
+
∂
∂
==
∂
∂
2
22
2
1
y
x
G
R
r
(19)
Коэффициенты
),(
η
ξ
E и ),(
η
ξ
G являются, как известно, коэффициентами 1-ой
квадратичной формы, поскольку
222
ηξ
GdEdRdRdds +== ),(
r
r
. Пользуясь
произволом в выборе положительной непрерывной функции
),(
η
ξ
H ,
обозначим её в виде
EG
H
H
⋅∆
=
),(
),(
η
ξ
ηξ
0
. Тогда система уравнений (16), с учетом
формул (18) и (19), примет следующий окончательный вид
.
),(
;
),(
ξ
η
ξ
ηη
η
ξ
ξ
∂
∂
⋅−=
∂
∂
⋅
∂
∂
⋅=
∂
∂
⋅
q
E
H
p
G
q
G
H
p
E
11
(20)
(Индекс «0» у
),(
η
ξ
H в силу произвола в её выборе опущен). Всевозможные
частные решения системы (20) с любыми положительными непрерывными
функциями
),(
η
ξ
H определяют ортогональную сеть направляющих
constp =),(
η
ξ
и constq =),(
η
ξ
, с помощью которой задаются цилиндрические
законы распределения ГНА в системе координат
),,( z
η
ξ
.
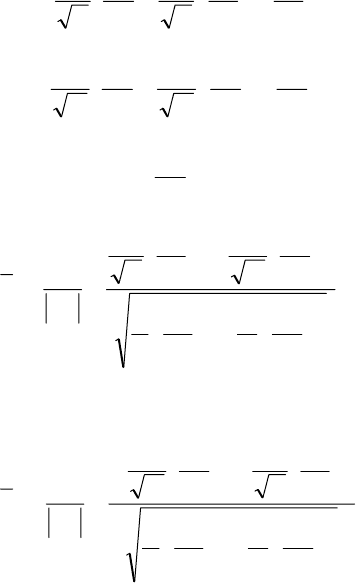
315
Вычислим компоненты тензора проницаемости для всех
рассматриваемых законов распределения ГНА в ортогональной системе
координат
),,( z
η
ξ
. С этой целью предварительно найдем разложения
векторов
321
eee
rrr
,, и
321
hhh
rrr
,, . Имеем:
;
∂
∂
+
∂
∂
=
∂
∂
⋅=
j
y
i
x
E
R
E
e
rr
r
r
ξξξ
11
1
(21)
;
∂
∂
+
∂
∂
=
∂
∂
⋅=
j
y
i
x
G
R
G
e
rr
r
r
ηηη
11
2
(22)
;k
z
R
e
r
r
r
=
∂
∂
=
3
(23)
;
22
21
1
11
11
∂
∂
+
∂
∂
∂
∂
⋅+
∂
∂
⋅
=
∇
∇
=
ηξ
ηξ
p
G
p
E
e
p
G
e
p
E
p
p
h
rr
(24)
с учетом системы уравнений (20):
;
22
21
2
11
11
∂
∂
+
∂
∂
∂
∂
⋅+
∂
∂
⋅−
=
∇
∇
=
ηξ
ξη
p
G
p
E
e
p
E
e
p
G
q
q
h
rr
(25)
keh
r
r
r
==
33
. (26)
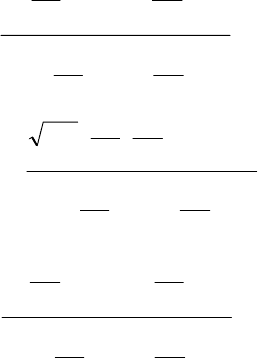
Теперь по формулам (П1.1.11) и (П1.3.6) для компонент тензора
проницаемости в координатах
),,( z
η
ξ
находим следующие значения:
316
=====
∂
∂
+
∂
∂
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
−⋅
∂
∂
⋅
∂
∂
⋅
==
∂
∂
+
∂
∂
∂
∂
+
∂
∂
=
.;
;
;
)(
;
33332233113
22
2
2
1
2
22
22
21
2112
22
2
2
1
2
11
0
λ
ηξ
λ
ξ
λ
η
ηξ
λλ
ηξ
ηξ
λ
η
λ
ξ
kkkkk
p
E
p
G
p
G
p
E
k
p
E
p
G
pp
EG
kk
p
E
p
G
p
E
p
G
k
(27)
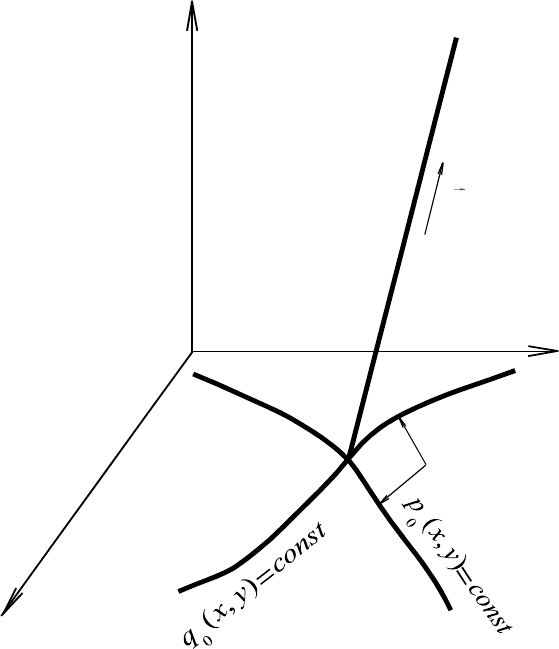
Рис. 69.
y
} , , { n
m
l
s
=
x
z
- образующа
я
цилиндрических
поверхностей
- направляющие
линии для
цилиндрических
поверхносетй

317
1
k
1
k
1
k
1
k
1
k
2
k
2
k
2
k
q
p
2
k
1
h
2
h
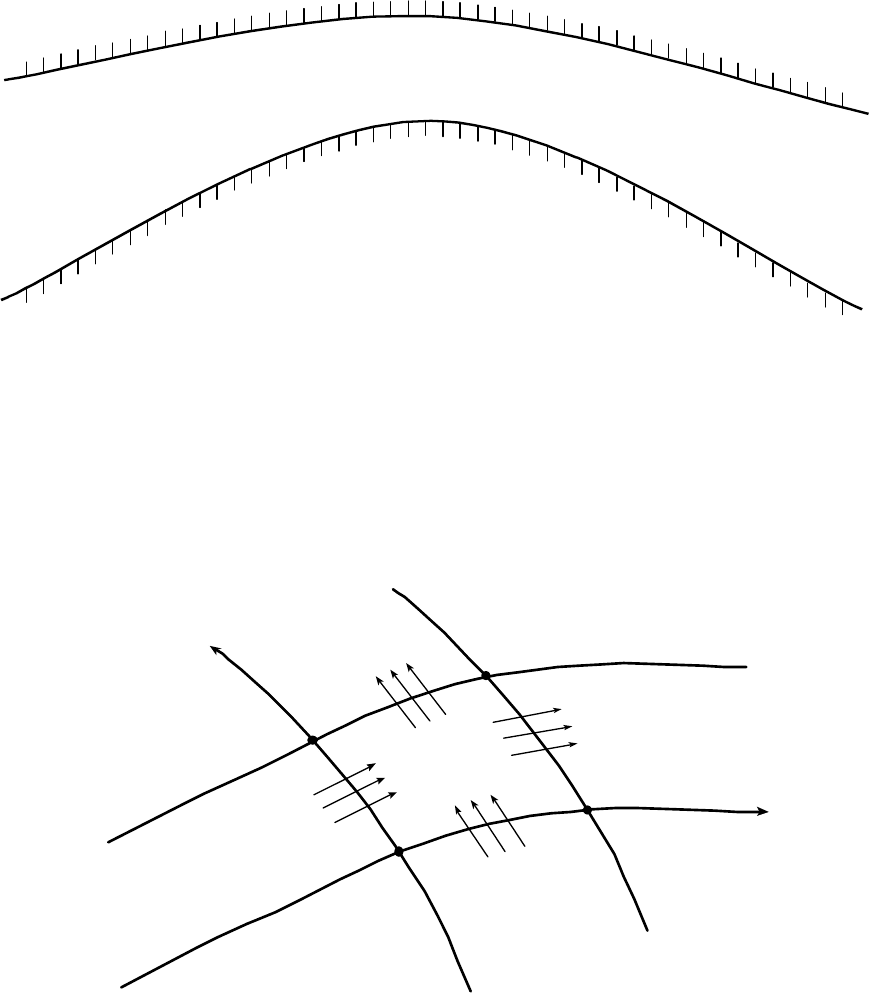
Рис. 1. Пример пористой среды с периодической структурой (многослойная
слоистая среда – МС-среда)
Рис. 2. Элементарный объём усреднения
ω
. Длина дуги ;AM
p
l=
′
;BM
q
l=
′
r
CM l=
′
. Прямые MA, MB, MC – оси локальной декартовой системы координат
r
~
,q
~
,p
~
.
C
C ’
B
B ’
A
A ’
M
r
R
∂
∂
r
p
R
∂
∂
r
q
R
∂
∂
r
318
2
1
3
Рис. 3. Типовая схема разреза продуктивного пласта. 1 - непроницаемая кровля
пласта (координатная поверхность ζ
2
=const); 2 – продуктивный пласт; 3 -
непроницаемая подошва пласта (координатная поверхность ζ
1
=const).
( , )
η
ξ
( +d , )
η
ξ
ξ
( , +d )
η
ξ
η
( +d , +d )
η
ξ
η
ξ
ξ
η
П
1
П
2
П
3
П
4
A
B
C
D
Рис. 4. Сечение АВСD элементарного криволинейного параллелепипеда
поверхностью ζ=const. Основания параллелепипеда расположены на
непроницаемых подошве (ζ=ζ
1
) и кровле (ζ=ζ
2
) слоя. Вдоль AD η=const; вдоль
ВС η+dη=const; вдоль AВ ξ=const; вдоль СD ξ+dξ=const.
