Тимофеев В.А., Тимофеев А.А. Краткий курс лекций по высшей математике. Семестр II (сокращенная программа)
Подождите немного. Документ загружается.

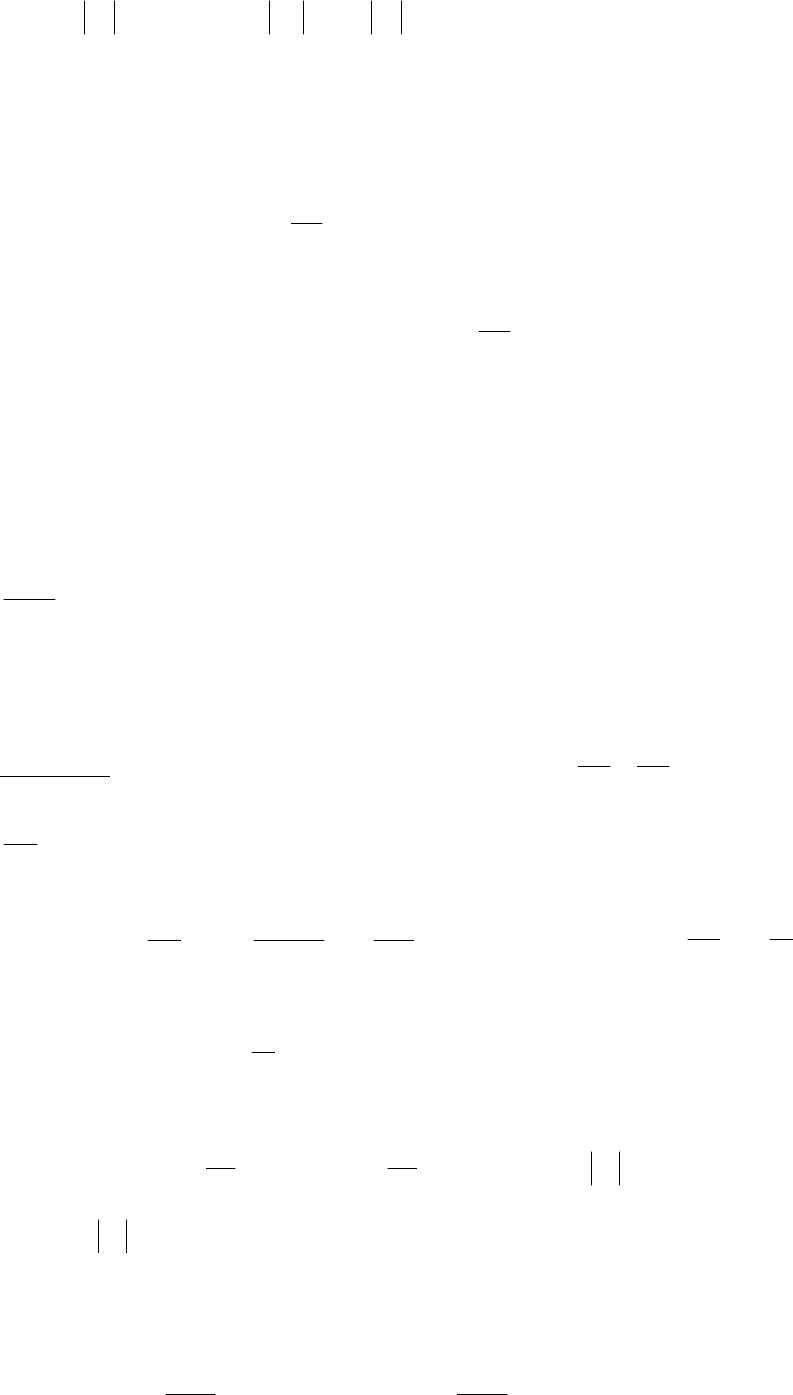
50
Cey
x
lnlnln
2
+=
−
,
2
lnln
x
Cey
−
=
,
– общее решение уравнения (*).
2
x
Cey
−
=
Пусть )(
x
C
C
= . Тогда – подставляем в исходное уравнение:
2
)(
x
exCy
−
⋅=
, ,
2222
)(22)()(
xxxx
xeexCxxexCexC
−−−−
=⋅⋅+⋅⋅−⋅
′
22
)(
xx
xeexC
−−
=⋅
′
xxC =
′
)(,
C
x
xC +=
2
)(
2
.
Таким образом, общее решение исходного уравнения:
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+⋅=
−
C
x
ey
x
2
2
2
.
Определение. Уравнение вида
, (
n
yxqyxpy )()( =+
′
1
≠
n ) (2)
называется уравнением Бернулли.
Чтобы его решить, надо обе части разделить на и сделать замену
n
y
z
y
n
=
−1
1
. После замены получается линейное уравнение.
Пример 2. Решить уравнение
33
22 yxxyy =+
′
.
Решение.
Разделим данное уравнение на :
3
y
3
33
2
2
x
y
x
y
y
=+
′
. После замены
z
y
=
2
1
получаем:
z
y
y
y
yy
y
′
=
′
−=
⋅
′
−=
′
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
342
221
, следовательно,
2
3
z
y
y
′
−=
′
.
Имеем:
3
22
2
xxz
z
=+
′
− ,
3
44
x
xz
z
=
+
′
−
. (**)
Решим уравнение
04
=
+
′
−
x
zz . (***)
x
zz 4=
′
, xdx
z
dz
4= ,
⎮
⌡
⌠
⎮
⌡
⌠
= xdx
z
dz
4, Cxz +=
2
2ln ,
Cez
x
lnlnln
2
2
+=
,
2
2x
Cez
=
– общее решение уравнения (***).
Пусть )(
x
C
C
= . Тогда – подставляем в уравнение (**):
2
2
)(
x
exCz ⋅=
, ,
3222
4)(44)()(
222
xexCxxexCexC
xxx
=⋅⋅+⋅⋅−⋅
′
−
32
4)(
2
xexC
x
=⋅
′
−
dx
e
x
xdC
x
2
2
3
4
)(
=− ,
⎮
⌡
⌠
=
⎮
⌡
⌠
− dx
e
x
xdC
x
2
2
3
4
)(.

51
Далее:
=
−=
=
=
=
=
⎮
⌡
⌠
=
⎮
⌡
⌠
===
⎮
⌡
⌠
=
⎮
⌡
⌠
−
−−−−
t
tttx
x
ev
dvdte
dtdutu
dttetdetxxdedx
e
x
2
2222242
2
3
,2
,,
2)()(
4
2
2
Cetedtete
tttt
+−−=
⎮
⌡
⌠
+−=
−−−− 2222
2
1
.
Таким образом,
CeexCetexC
xxtt
++=++=
−−−−
22
22222
2
1
2
1
)(
,
следовательно,
2222
222222
2
1
2
1
xxxx
CexeCeexz ++=⋅
⎟
⎠
⎞
⎜
⎝
⎛
++=
−−
,
2
11
22
2
2
++= xCe
y
x
.
§ 6. Дифференциальные уравнения высших порядков
6.1 Дифференциальные уравнения второго порядка
Определение. Дифференциальное уравнение вида 0);;;(
=
′
′
′
yyyxF
, в
левую часть которого входит вторая производная, называется дифференци-
альным уравнением 2-го порядка.
Определение. Уравнение вида
);;( yyxfy
′
=
′
′
называется разрешен-
ным относительно второй производной.
Пример 1. Решить уравнение xy
=
′
′
.
Решение. Последовательно интегрируя, найдем:
1
2
2
C
x
y +=
′
,
21
3
1
2
62
CxC
x
dxC
x
y ++=
⎮
⌡
⌠
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+=
.
Дифференциальное уравнение второго порядка );;( yyxfy
′
=
′′
имеет
бесчисленное множество решений, которые даются формулой
);;(
21
CCxy
ϕ
= , содержащей две произвольные постоянные. Эта совокуп-
ность решений называется общим решением.
Частное решение уравнения отыскивается при помощи задания началь-
ных условий
0
0
yy
xx
=
=
и
0
0
yy
xx
′
=
′
=
.
Пример 2. Найти частное решение уравнения
xy =
′
′
при начальных условиях
2
2
=
=x
y , 3
2
=
′
=x
y .
Решение.
Выше мы нашли общее решение –
21
3
6
CxC
x
y ++= . Подставляя
начальные условия в выражения для общего решения и его производной, по-
лучим систему уравнений:

52
⎩
⎨
⎧
−=
=
⇒
⎩
⎨
⎧
++=
+=
.34
,1
,2342
,23
2
1
21
1
C
C
CC
C
Таким образом, частное решение имеет вид
3
4
6
3
−+= x
x
y .
6.2 Дифференциальные уравнения высших порядков
Определение. Порядком дифференциального уравнения называют
наивысший порядок производной, входящей в уравнение.
Определение. Дифференциальное уравнение -го порядка вида
называется разрешенным относительно старшей
производной.
n
)...;;;;(
)1()( −
′
=
nn
yyyxfy
Общее решение такого уравнения зависит от произвольных постоян-
ных:
n
)...;;;;(
21 n
CCCxy
ϕ
=
.
Чтобы выделить частное решение, отвечающее конкретным условиям
задачи, нужно задать начальные условия, они имеют следующий вид
0
0
yy
xx
=
=
,
0
0
yy
xx
′
=
′
=
, …,
)1(
0
)1(
0
−
=
−
=
n
xx
n
yy
,
т.е. при задаются значения самой функции и ее первых ) произ-
водных. Дифференцируя )
0
xx = 1( −n
1(
−
n раз общее решение и подставляя начальные
условия, мы получим систему уравнений с неизвестными , , …,
.
n n
1
C
2
C
n
C
6.3 Дифференциальные уравнения, допускающие понижение порядка
1. Уравнения вида
)(
)(
xfy
n
= .
Последовательно интегрируя раз, находим общее решение. n
2. Если в уравнение не входит искомая функция , т.е. оно имеет вид y
0)...;;;;(
)()1()(
=
+ nkk
yyyxF
,
то порядок уравнения можно понизить, взяв за новую неизвестную функцию
низшую из производных, входящих в уравнение, т.е. сделав замену .
zy
k
=
)(
Пример 1. Решить уравнение x
x
y
y =
′
+
′′
.
Решение.
Уравнение не содержит , поэтому замена , y zy =
′
zy
′
=
′′
. После
подстановки получаем
x
x
z
z =+
′
– линейное уравнение.

53
Решим уравнение
0=+
′
x
z
z . (*)
Имеем:
x
z
z −=
′
,
x
z
dx
dz
−=
,
x
dx
z
dz
−=
,
⎮
⌡
⌠
−=
⎮
⌡
⌠
x
dx
z
dz
,
Cxz lnlnln
+
−= ,
x
C
z = – общее решение уравнения (*).
Пусть )(
x
C
C
= , тогда
x
xC
z
)(
= и подставляем в линейное уравнение.
Имеем:
x
x
xC
x
xCxxC
=+
−
⋅
′
22
)()()(
,
x
x
xC
x
xC
x
xC
=+−
′
)()()(
,
,
2
)( xxC =
′
1
3
3
)( C
x
xC += , следовательно,
x
Cx
z
1
2
3
+= .
Тогда:
x
C
x
y
1
2
3
+=
′
,
⎮
⌡
⌠
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+= dx
x
C
x
y
1
2
3
,
21
3
ln
9
CxC
x
y ++= – общее решение.
3. Если в уравнение не входит независимая переменная
x
, т.е. уравнение
имеет вид
0)...;;;;(
)(
=
′′′
n
yyyyF ,
то порядок уравнения можно понизить, взяв за новую независимую перемен-
ную , а за неизвестную функцию y )( ypy
=
′
.
Пример 2. Решить уравнение .
2
)( yyy
′
=
′′
Решение.
В уравнение не входит переменная
x
, поэтому замена )(ypy
=
′
.
Тогда
pp
dx
dy
dy
dp
dx
ydp
dx
yd
y ⋅
′
=⋅==
′
=
′′
)(
.
После подстановки имеем:
2
pppy =⋅
′
⋅ , , ppy =
′
⋅
y
dy
p
dp
=
,
1
lnlnln Cyp
+
=
, . yCp
1
=
Тогда
, yCyp
1
=
′
=
dxC
y
dy
1
=
,
⎮
⌡
⌠
=
⎮
⌡
⌠
dxC
y
dy
1
,
21
ln CxCy += ,
2
lnlnln
1
Cey
xC
+= , ,
xC
eCy
1
1
= consty
=
(при делении на
p
потеряно решение 0
=
p
, 0
=
′
y , ). consty =

54
§ 7. Линейные дифференциальные уравнения высших порядков
7.1 Линейные уравнения второго порядка. Общие свойства
Определение. Линейным дифференциальным уравнением 2-го поряд-
ка называется уравнение первой степени (линейное) относительно неизвест-
ной функции и ее производных. Будем записывать его в виде
)()()(
21
xfyxayxay
=
+
′
+
′′
. (1)
Функция )(
x
f
называется правой частью уравнения. Если функция
)(
x
f
тождественно равна нулю, то уравнение (1) называется линейным
уравнением без правой части (или однородным). В противном случае урав-
нение (1) называется линейным уравнением с правой частью (или неодно-
родным).
Если в некотором интервале b
x
a
≤
≤
функции , и )) )(
2
xa(
1
xa (
x
f
не-
прерывны, то уравнение (1) при любых начальных условиях
0
0
yy
xx
=
=
,
0
0
yy
xx
′
=
′
=
, где );(
0
bax
∈
имеет единственное решение, удовлетворяющее этим условиям.
7.1.1 Линейные уравнения без правой части
Рассмотрим уравнение без правой части
0
21
=
+
′
+
′
′
yayay , (2)
где и . В частных случаях и могут быть просто
постоянными.
)
)
(
11
xaa = )(
22
xaa =
1
a
2
a
Теорема. Если и ) – решения линейного уравнения (2), то
функция
(
1
xy
)( Cx
(
2
xy
)(
2
xy)(
211
yCxy
⋅
+⋅
=
при любых постоянных и также
является решением уравнения.
1
C
2
C
Следствие. Если и – решения (2) такие, что их отношение не
равно постоянной величине (
1
y
2
y
constyy
≠
12
), то линейная комбинация этих
функций является общим решением уравнения.
2
y⋅
211
CyCy +⋅=
Из общего решения при любых заданных возможных начальных усло-
виях может быть найдено частное решение, удовлетворяющее этим услови-
ям.
Пусть заданы начальные условия
0
0
yy
xx
=
=
,
0
0
yy
xx
′
=
′
=
, причем
точка принадлежит интервалу, где функции и непрерывны. В
частности, если и – постоянные, то может быть любым. Подставляя
начальные значения в выражения для общего решения и его производной,
получим систему линейных алгебраических уравнений относительно и
:
0
x )(
1
xa )(
2
xa
1
a
2
a
0
x
1
C
2
C

55
⎩
⎨
⎧
′
=
′
⋅+
′
⋅
=⋅+⋅
,
,
0202101
0202101
yyCyC
yyCyC
где , ,
)(
0110
xyy = )(
0110
xyy
′
=
′
)(
0220
xyy
=
,
)(
0220
xyy
′
=
′
– известные числа.
Чтобы эта система имела решение при любых правых частях, необхо-
димо и достаточно, чтобы определитель системы был не равен нулю:
0
2010
2010
≠
′′
yy
yy
. (3)
Если определитель равен нулю, то система имеет решение только при
условии
0
0
20
20
10
10
y
y
y
y
y
y
′
=
′
=
′
, т.е. заведомо не при любых начальных условиях
и .
0
y
0
y
′
7.1.2 Линейные уравнения с правой частью
Пусть дано линейное уравнение 2-го порядка с правой частью
)(
21
xfyayay
=
+
′
+
′
′
. (1)
Уравнение без правой части
0
21
=
+
′
+
′
′
yayay (2)
называется соответствующим уравнению (1).
Теорема. Общее решение уравнения с правой частью (1) можно соста-
вить как сумму общего решения соответствующего уравнения без правой
части (2) и какого-нибудь частного решения данного уравнения (1).
Таким образом, чтобы найти общее решение уравнения с правой ча-
стью, нужно найти общее решение соответствующего уравнения без правой
части и лишь одно какое-нибудь частное решение заданного уравнения. Это
можно записать так:
)(
2211
xyCyCy
ϕ
+
⋅
+
⋅
=
,
где и – частные решения соответствующего уравнения без правой час-
ти, а )
1
y
2
y
(
x
ϕ
– частное решение уравнения с правой частью.
7.2 Уравнения 2-го порядка с постоянными коэффициентами
без правой части
Рассмотрим линейное уравнение с постоянными коэффициентами
)(
21
xfyayay
=
+
′
+
′
′
, (1)
где и – постоянные величины.
1
a
2
a
Возьмем однородное линейное уравнение 2-го порядка
0
21
=
+
′
+
′
′
yayay , (2)
где и – постоянные величины.
1
a
2
a

56
Найдем решение такого уравнения.
Возьмем функцию вида (
rx
ey =
r
– константа). Подставим ее в урав-
нение (2):
rx
rey =
′
, ,
rx
ery
2
=
′′
следовательно, имеет место тождество
, или, т.к. 00)(
21
2
=++ arare
rx
≠
rx
e ,
0. (4)
21
2
=++ arar
Отсюда видно, что функция будет решением дифференциального
уравнения (2), если
rx
e
r
будет корнем квадратного уравнения (4).
Уравнение (4) называется характеристическим.
Чтобы составить характеристическое уравнение, нужно в данном диф-
ференциальном уравнении (2) заменить единицей, а каждую производную
искомой функции ( и ) – величиной
y
y
′
y
′′
r
в степени, равной порядку произ-
водной (
r
и
2
r
).
Возможны три случая для корней и характеристического уравне-
ния (предполагается, что и – действительные числа):
1
r
2
r
1
a
2
a
1) и – действительные и различные числа: ;
1
r
2
r
21
rr ≠
2) и – действительные и равные числа: ( – двукратный
корень уравнения (4);
1
r
2
r
21
rr =
1
r
3) и – комплексные сопряженные числа:
1
r
2
r ir
β
α
+=
1
,
ir
β
α
−
=
2
,
0≠
β
.
Случай 1:
.
21
rr ≠
Общее решение в случае действительных и разных корней характери-
стического уравнения дается формулой
xrxr
eCeCy
21
21
⋅+⋅= ,
где и – произвольные постоянные.
1
C
2
C
Легко проверить, что определитель (3) в данном случае не равен нулю;
составим этот определитель, задаваясь каким-нибудь значением :
0
x
)(
12
)(
21
021
0201
0201
rre
erer
ee
xrr
xrxr
xrxr
−=
+
.
Т.к. , то этот определитель ни при каком значении не равен
нулю.
21
rr ≠
0
x
Пример 1. Решить уравнение
02
=
−
′
−
′
′
yyy
.
Решение. Составим характеристическое уравнение:
02
2
=−−
r
r
. Его корни
и . Общее решение имеет вид
2
1
=r 1
2
−=r
xx
eCeCy
−
⋅+⋅=
2
2
1
.
57
Найдем частное решение по ным условиям: началь
2
0
=
=x
y и 5
0
−
=
′
=x
y .
Составим систему уравнений относительно и :
Искомое частное решение .
1
C
2
C
⎩
⎨
⎧
−=
⇒
⎨
⎧
−
=+
.3
,1
,5
,2
2
121
C
CCC
=
⎩
=−2
21
CC
xx
eey
−
+−= 3
2
Случай 2:
21
rr = .
В случае действительных равных корней характеристического уравне-
ния общее решение уравнения (2) имеет вид
, что определитель (3) ни при каком значении не
равен нулю:
xr
exCCy
1
)(
21
⋅+=
.
Легко проверить
0
x
0
01
010101
0101
2
011
0
≠=
+
xr
xrxrxr
xrxr
e
exreer
exe
.
096
=
+
′
−
′
′
yyy
Пример 2. Решить уравнение .
ристичес
Решение. Характе кое уравнение 96
2
0
=
+
−
r
r
имеет один дву-
кратный корень . Общее решение
.
3
21
== rr имеет вид
x3
exCCy
21
)( ⋅+=
Случай 3: корни характеристического уравнения – комплексные со-
пряженные числа
ir
β
α
+=
1
, ir
β
α
−
=
2
.
В случае комплексных сопряженных корней характеристического
уравнения общее решение имеет вид
. )sincos(
2
xCxCey
x
ββ
α
+=
1
0134
=
+
′
−
′
′
yyy
Пример 3. Решить уравнение .
ское уравнение
Решение. Характеристиче
0134
2
=
+
−
r
r
имеет комплекс-
ные сопряженные корни
ir 32
1
+
=
и
i32r
2
−
=
. Общее решение имеет вид
.
7.3 Уравнения 2-го пор ми коэффициентами
ейное уравнение с постоянными коэффициентами и
й частью
)3sin3cos(
21
xCxCey +=
2x
ядка с постоянны
с правой частью
Рассмотрим лин
1
a
2
a и с право
)(
21
xfyayay
=
+
′
+
′
′
. (1)

58
Общее решение уравнения (1) есть сумма общего решения соответст-
вующего уравнения без правой части и частного решения уравнения с правой
частью.
Общее решение уравнения без правой части мы умеем находить. Най-
дем частное решение уравнения (1).
Рассмотрим некоторые частные случаи, в которых решение находится
методом неопределенных коэффициентов.
1. Пусть правая часть уравнения (1) имеет вид
, (5)
mx
exPxf ⋅= )()(
где )(
x
P
– многочлен. Тогда уравнение (1) имеет частное решение вида
, (6)
mxk
exQxy ⋅⋅= )(
где )(
x
Q – многочлен той же степени, что и )(
x
P
, причем, если число не
является корнем характеристического уравнения , то
m
0
21
2
=++ arar 0
=
k
, а
если является, то
k
– кратность этого корня.
Принимая решение в указанной форме, мы находим неизвестные ко-
эффициенты многочлена )(
x
Q по методу неопределенных коэффициентов.
Правило сохраняет свою силу и тогда, когда 0
=
m , т.е. в правой части
стоит только многочлен; в этом случае надо проверить, не является ли число
корнем характеристического уравнения. В частных случаях многочлен 0
)(
x
P
может быть нулевой степени, т.е. постоянной величиной.
Пример 4. Решить уравнение xyyy
+
=
+
′
−
′
′
12.
Решение. Характеристическое уравнение 012
2
=
+
−
r
r
имеет корень 1
=
r
кратности 2. Общее решение однородного уравнения
x
одн
exCCy ⋅+= )(
21
.
Правая часть уравнения имеет форму (5), причем 0
=
m ,
x
x
P
+= 1)(. Т.к. 0 не
является корнем характеристического уравнения, то частное решение ищем в
виде
BAxy
част
+
=
,
где
A
,
B
– постоянные, подлежащие отысканию.
Дифференцируя и подставляя в дифференциальное уравнение, находим
x
B
Ax
A
+
=
+
+
−
12.
Приравнивая коэффициенты в обеих частях равенства при подобных членах
1
=
A
, 12
=
+
−
B
A
,
находим
1=
A
, 3=
B
. Таким образом, частное решение имеет вид
3
+
=
xy
част
.
Общее решение
)3()(
21
++⋅+=+= xexCCyyy
x
частодн
.
Пример 5. Решить уравнение .
x
eyyy
2
334 =+
′
−
′′
Решение. Характеристическое уравнение 034
2
=
+
−
r
r
имеет корни 1
=
r
,

59
3
=
r
. Общее решение однородного уравнения
xx
одн
eCeCy
3
21
⋅+⋅= .
Правая часть уравнения имеет форму (5), причем 3)(
=
x
P
; – не явля-
ется корнем характеристического уравнения, поэтому
2=m
0
=
k
.
Частное решение ищем в виде
x
eAy
2
⋅= ,
A
– постоянная, подлежащая отысканию. Тогда где
x
Aey
2
2=
′
, .
x
Aey
2
4=
′′
Подставляя , , в исходное уравнение, получим
y
y
′
y
′′
xxxx
e
A
e
A
e
A
e
2222
3384
=
+
−
, откуда 3−=
A
.
Следовательно,
x
част
ey
2
3−= ,
общее решение исходного уравнения
xxx
частодн
eeCeCyyy
23
21
3−⋅+⋅=+= .
2. Пусть правая часть уравнения (1) имеет вид
nxbnxa
x
f
sincos)(
+
=
.
Если числа не являются корнями характеристического уравнения,
то уравнение имеет частное решение вида
in±
nx
B
nx
A
y sincos
+
=
.
Если же числа служат корнями характеристического уравнения, то
частное решение имеет вид
in±
)sincos(
nx
B
nx
A
x
y
+
⋅
=
.
В частных случаях, когда 0
=
a или 0
=
b , решение все равно следует
искать в указанном полном виде.
Пример 6. Решить уравнение xyyy 2sin5134
=
+
′
+
′
′
.
Решение. Характеристическое уравнение 0134
2
=
+
+
r
r
имеет корни
r
i32 ±−= . Общее решение однородного уравнения
)3sin3cos(
21
2
xCxCey
x
одн
+=
−
.
Т.к. числа не являются корнями характеристического уравнения, то ча-
стное решение ищем в виде
i2±
xBxAy
част
2sin2cos
+
=
.
Дважды дифференцируем:
xBxAy 2cos22sin2 +
−
=
′
, xBxAy 2sin42cos4
−
−
=
′
′
.
Полученные выражения подставим в уравнение:
A
x
x
B
x
A
x
B
x
A
x
B
x
4 2sin52sin132cos132cos82sin82sin42cos = . −
+
+
+
−−
Приравнивая друг другу коэффициенты при
x
2sin и
x
2cos в обеих частях
равенства, получим:
