Тимофеев В.А., Тимофеев А.А. Краткий курс лекций по высшей математике. Семестр II (сокращенная программа)
Подождите немного. Документ загружается.

40
Правая часть соотношения (2) является интегральной суммой непре-
рывной на ] функции ;[ ba
[]
2
)(1 xf
′
+
.
L
A
B
≈
∪
. Приближение будет тем
точнее, чем меньше шаг разбиения. Отсюда длина дуги
∪
A
B будет равна пре-
делу интегральных сумм (2) при условии, что шаг разбиения стремится к 0,
т.е.
[] []
⎮
⌡
⌠
′
+=Δ⋅
′
+=
∑
=
→
∪
b
a
n
i
ii
dxxfxcfAB
2
1
2
0
)(1)(1lim
λ
,
{}
n
xx
Δ
Δ= ...,,max
1
λ
.
Пример 1.
Найти длину дуги кривой 2
32
xy = от 0
=
x
до 1=
x
.
Решение.
[]
=
⎮
⌡
⌠
+==
′
==
⎮
⌡
⌠
′
+= dxxxy
x
ydxxfL
1
0
21
23
1
0
2
8
9
1
22
3
,
2
)(1
=⋅=
⎮
⌡
⌠
=
=⇒==⇒=
==+
=
1
817
23
817
1
21
3
2
9
8
9
8
8
17
1,10
9
8
,
8
9
1
uduu
uxux
dudxux
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
⎟
⎠
⎞
⎜
⎝
⎛
= 1
8
17
27
16
23
.
9.2 Вычисление длины дуги кривой,
заданной параметрическими уравнениями
Пусть кривая
∪
A
B задана параметрическими уравнениями:
βα
≤≤
⎩
⎨
⎧
=
=
t
tyy
txx
),(
),(
.
Функции )(
t
x
, )(
t
y , ,
)(tx
′
)(ty
′
непрерывны и
0)( >
′
tx
на ];[
β
α
.
Имеем:
t
t
x
y
dx
dy
xf
′
′
==
′
)(;
[] [][]
dttytxdttx
x
y
dxxf
t
t
22
2
2
)()()(1)(1
′
+
′
=
′
⋅
⎥
⎦
⎤
⎢
⎣
⎡
′
′
+=
′
+ ;
[] [][]
dttytxdxxfAB
b
a
⎮
⌡
⌠
′
+
′
=
⎮
⌡
⌠
′
+=
∪
β
α
222
)()()(1 . (2)

41
Пример 2.
Вычислить длину дуги кривой t
t
x −=
3
3
, от 0
2
2
+= ty
=
t
до 3
=
t
.
Решение.
[][]
=
⎮
⌡
⌠
+−=
⎮
⌡
⌠
′
+
′
=
3
0
222
22
4)1()()( dtttdttytxL
β
α
1239
3
)1(12
0
3
3
3
0
2
3
0
24
=+=+=
⎮
⌡
⌠
+=
⎮
⌡
⌠
++= t
t
dttdttt .
9.3 Вычисление длины дуги кривой в полярной системе координат
Пусть кривая
∪
A
B задана уравнением в полярных координатах
)(
ϕ
ρ
ρ
= ,
β
ϕ
α
≤≤ , причем )(
ϕ
ρ
и )(
ϕ
ρ
′
– непрерывные на ];[
β
α
функ-
ции.
Имеем:
⎩
⎨
⎧
=
=
,sin
,cos
ϕρ
ϕ
ρ
y
x
(
ϕ
взяли за параметр);
ϕ
ρ
ϕ
ρ
ϕ
sincos ⋅−⋅
′
=
′
x ;
ϕ
ρ
ϕ
ρ
ϕ
cossin
⋅
+
⋅
′
=
′
y ;
[] []
+⋅
′
+⋅+
′
−⋅
′
=
′
+
′
ϕρϕρϕϕρρϕρ
ϕϕ
222222
22
sinsincossin2cosyx
ρρϕρϕϕρρ
+
′
=⋅+
′
+
222
coscossin2.
Тогда
[] []
ϕρρϕ
β
α
β
α
ϕϕ
ddyxAB
⎮
⌡
⌠
′
+=
⎮
⎮
⌡
⌠
′
+
′
=
∪
22
22
. (3)
Пример 3.
Найти длину кривой
ϕ
ρ
sin2
=
.
Решение. Линия
ϕ
ρ
sin2= представляет собой “однолепестковую розу”
(
π
ϕ
ϕ
ρ
≤≤⇒≥⇒≥ 00sin0). Тогда длина
искомой кривой (рис. 5.11) равна
Рис. 5.11
O
l
2
=
⎮
⌡
⌠
+=
⎮
⌡
⌠
′
+=
ϕϕϕϕρρ
π
β
α
ddL
0
2222
cossin2
πϕ
π
22
0
=
⎮
⌡
⌠
= d .

42
§ 10. Объем тела
Пусть дано тело, ограниченное замкнутой поверхностью, и пусть из-
вестна площадь любого его сечения, произведенного плоскостью, перпенди-
кулярной к некоторой прямой, например, к оси абсцисс (рис. 5.12).
При этом можно
считать, что площадь
такого сечения является
известной нам функци-
ей )(
x
S
, где
x
– абс-
цисса точки пересече-
ния указанной плоско-
сти с осью
x
.
Предположим да-
лее, что все тело за-
ключено между двумя
перпендикулярными к
оси
x
плоскостями, пересекающими ее в точках и ( ). Для опреде-
ления объема такого тела разобьем его на слои с помощью секущих плоско-
стей, перпендикулярных к оси
a b ba <
x
и пересекающих ее в точках , , ,
…, . Заменим каждый слой прямым цилиндром с той же высотой и ос-
нованием, равным ); объем прямого цилиндра равен произведению пло-
щади его основания на высоту. Поэтому объем -ступенчатого тела выразит-
ся суммой
ax =
0 1
x
2
x
b=x
n
(
i
xS
n
Рис. 5.12
a
1
x
2
x
b
x
∑
−
=
−−
Δ=−++−+−=
1
0
11121010
)())((...))(())((
n
i
iinnnn
xxSxxxSxxxSxxxSV .
Предел полученной суммы, а она является интегральной суммой для функ-
ции )(
x
S
на отрезке ], при ;[ ba
∞
→n и при стремлении наибольшего
i
x
Δ
к
нулю и даст нам искомый объем
. (1)
⎮
⌡
⌠
=
b
a
dxxSV )(
Если рассматриваемое тело получается вращением криволинейной тра-
пеции, ограниченной линией )(
x
f
y
=
вокруг оси O
x
, то поперечным сече-
нием с абсциссой
x
служит круг, радиус которого равен соответствующей
ординате линии )(
x
f
y = . (Если 0
<
y , то радиус равен y .) В этом случае
2
)( yxS
π
=
,
и мы приходим к формуле для объема тела вращения
, где
⎮
⌡
⌠
=
b
a
dxyV
2
π
)(
x
f
y
=
. (2)
43
Пример.
Найти объем трехосного эллипсоида 1
2
2
2
2
2
2
=++
c
z
b
y
a
x
.
Решение.
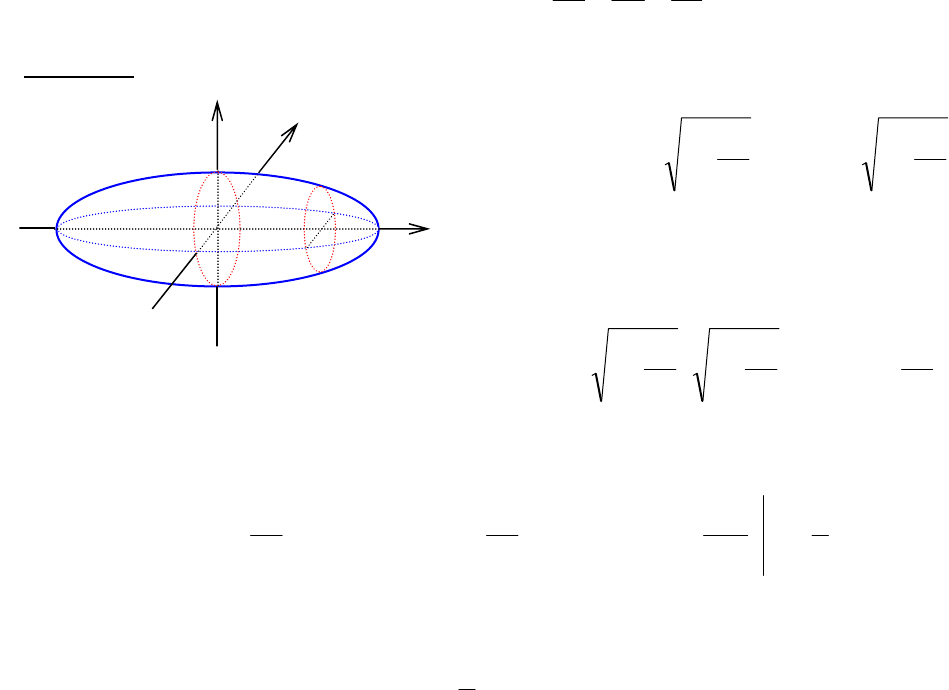
Его плоскими сечениями, перпендикулярными, например, к оси
O
x
(рис. 5.13), являются эллипсы с по-
луосями
2
2
1
a
x
b − и
2
2
1
a
x
c − ,
a
x
a
≤
≤
−
.
Рис. 5.13
z
y
b
a
c
O
x
Площадь )(
x
S
поперечного сече-
ния в точке
x
известна:
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=−−=
2
2
2
2
2
2
111)(
c
x
bc
a
x
c
a
x
bxS
ππ
;
поэтому
abc
a
x
xbcdx
a
x
bcdx
a
x
bcV
a
aa
a
ππππ
3
4
3
2121
0
2
3
0
2
2
2
2
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
⎮
⌡
⌠
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
⎮
⌡
⌠
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
−
.
Если две из полуосей равны между собой, например, , то эллипсо-
ид превращается в шар объема
bc =
3
3
4
aV
π
= .

44
Глава VI
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
§ 1. Задачи, приводящие к понятию дифференциального уравнения
1
0
. Радиоактивный распад. Экспериментальным путем установлено,
что скорость радиоактивного распада пропорциональна количеству нерас-
павшегося вещества. Считая, что начальное количество вещества равна ,
найдем зависимость между количеством нераспавшегося вещества
0
M
M
и вре-
мени
t
.
Скорость радиоактивного распада равна производной от количества
вещества
M
по времени
t
, т.е.
dt
dM
. Но по условию
kM
dt
dM
−=
, (1)
где
k
– коэффициент пропорциональности. Знак минус берется потому, что с
возрастанием
t
количество вещества
M
уменьшается. Полученное уравне-
ние (1) называется математической моделью данного физического процесса.
2
0
. Охлаждение тела. Согласно закону, установленному Ньютоном,
скорость охлаждения тела пропорциональна разности между температурой
тела и температурой окружающей среды.
Пусть тело нагрето до температуры ; температуру окружающей сре-
ды будем считать постоянной и равной (
0
T
T
cc
T
0
T
<
). Найдем зависимость ме-
жду изменяющей температурой
T
тела и временем охлаждения
t
.
Пусть в момент времени
t
температура тела равна
T
. Скорость изме-
нения температуры, т.е.
d
t
dT
по закону Ньютона пропорциональна разности
, следовательно,
c
TT −
)(
c
TTk
d
t
dT
−−= . (2)
Знак минус выбран потому, что с возрастанием
t
температура
T
тела
уменьшается. Коэффициент пропорциональности
k
зависит как от физиче-
ских свойств тела, так и от его геометрической формы.
§ 2. Дифференциальные уравнения 1-го порядка.
Общие понятия. Теорема существования
В уравнениях (1) и (2) § 1 наряду с известной функцией входит и ее
производная. Эти уравнения называются дифференциальными уравнениями.
Определение. Уравнение )(xfy
=
′
или dx
x
f
dy )(
=
, (1)
где – неизвестная функция от y
x
, а )(
x
f
– заданная функция, называется
простейшим дифференциальным уравнением.

45
Для решения уравнения (1) нужно проинтегрировать данную функцию
)(
x
f
. При этом мы получим бесчисленное множество функций, каждая из
которых будет удовлетворять условию (1), т.е.
Cdxxfy +
⎮
⌡
⌠
= )(.
Определение. Дифференциальным уравнением 1-го порядка называ-
ется уравнение, связывающее независимую переменную, неизвестную функ-
цию и ее производную.
Т.к. производную можно представить в виде отношения дифференциа-
лов, то уравнение может содержать не производную, а дифференциалы неиз-
вестной функции и независимой переменной.
Уравнения, в которых неизвестная функция зависит от одного аргумен-
та, называется обыкновенным дифференциальным уравнением.
Дифференциальное уравнение 1-го порядка в общем виде записывается
так:
0);;(
=
′
yyxF .
В частных случаях в левую часть уравнения могут не входить
x
или ,
но всегда обязательно входит
y
y
′
.
Определение. Уравнение вида );( yxfy
=
′
называется разрешенным
относительно производной.
Определение. Решением дифференциального уравнения называется
функция, которая при подстановке ее вместе с производной в это уравнение
превращает его в тождество.
Пример 1. Уравнение
x
y
y =
′
имеет решениями функции C
x
y
=
,
C
– любое число.
Любое дифференциальное уравнение );(
yxfy
=
′
имеет бесчисленное
множество решений, которые определяются формулой, содержащей одну
произвольную постоянную. Эту совокупность решений будем называть об-
щим решением дифференциального уравнения 1-го порядка и записывать
так:
);(
C
x
y
ϕ
=
.
Придавая произвольной постоянной
C
определенные числовые значе-
ния, мы будем получать частные решения.
Чтобы из общего решения выделить частное решение, необходимо за-
дать начальное условие. Задать начальное условие дифференциального урав-
нения 1-го порядка это значит указать пару соответствующих друг другу зна-
чений независимой переменной и функции :
0
x
0
y
0
0
yy
xx
=
=
.

46
Пример 2.
Найти частное решение дифференциального уравнения
x
y
y =
′
, 6
2
=
=x
y .
Решение. Уравнение имеет общее решение C
x
y
=
(см. пример 1). Подстав-
ляя начальное условие в общее решение, имеем
26
⋅
=
C
, следовательно, 3
=
C
.
Таким образом, функция
x
y 3
=
удовлетворяет дифференциальному уравне-
нию и начальному условию.
Теорема (существования и единственности решения).
Если функция );( y
x
f
непрерывна в области, содержащей точку
, то уравнение
);(
000
yxP );( yxfy
=
′
имеет решение )(
x
yy = такое, что
.
00
)( yxy =
Если, кроме того, непрерывна и частная производная
дy
дf
, то это реше-
ние единственно.
Теорема впервые была сформулирована и доказана Коши. Задачу по
отысканию частного решения по начальным условиям называют задачей
Коши.
График любого частного решения дифференциального уравнения на-
зывается интегральной кривой. Общему решению соответствует семейство
интегральных кривых.
Пример 3.
x
y
y =
′
.
Общее решение –
C
x
y
=
, соответствующее семейство интегральных
кривых – пучок прямых, проходящих через начало координат.
Задание начального условия
0
0
yy
xx
=
=
означает задание точки
, через которую должна проходить интегральная кривая, соответст-
вующая искомому частному решению, т.е. из семейства кривых мы выбираем
ту, которая проходит через точку ). Согласно теореме существова-
ния и единственности решения, через каждую точку, в которой функции
);(
000
yxP
;(
000
yxP
);(
y
x
f
и
дy
дf
непрерывны, проходит единственная интегральная кривая. Ес-
ли в данной точке эти условия нарушены, то это означает, что через эту точ-
ку либо вообще не проходит ни одна интегральная кривая, либо проходит не-
сколько.
Общее решение );(
C
x
y
ϕ
= дифференциального уравнения );( yxfy
=
′
обладает тем свойством, что из него по любому заданному возможному на-

47
чальному значению
0
0
yy
xx
=
=
может быть найдено частное решение, удов-
летворяющее этому условию.
Геометрическое место точек плоскости );(
y
x
, в которых наклон каса-
тельных к решениям уравнения
);( yxfy
=
′
один и тот же, называется изо-
клиной. Уравнение изоклины имеет вид
k
y
x
f
=
);(, где
k
– постоянная.
Чтобы приближенно построить решения уравнения );(
x yf=y
′
, можно на-
чертить достаточное число изоклин, а затем провести решения, т.е. кривые,
которые в точках пересечения с изоклинами ,
1
) k= ;(x;(xf y
2
) kyf
=
, …
имеют касательные с угловыми коэффициентами соответственно , , ….
1
k
2
k
§ 3. Уравнения с разделяющимися переменными
Рассмотрим уравнение вида
dxxfdyyf )()(
21
=
, (1)
где и – заданные функции.
)(
1
yf )(
2
xf
В этом дифференциальном уравнении переменные разделены, т.е. каж-
дая из переменных содержится только в той части уравнения, где находится
ее дифференциал.
В обеих частях уравнения (1) стоят дифференциалы некоторых функ-
ций; справа этот дифференциал выражен прямо через независимую перемен-
ную
x
, а слева через промежуточный аргумент , который является функци-
ей от
y
x
. Именно эта зависимость от y
x
и является искомой. Произведя ин-
тегрирование, мы получим связь между переменными
x
и , освобожден-
ную от их дифференциалов:
y
⎮
⌡
⌠
⎮
⌡
⌠
= dxxfdyyf )()(
21
.
Если задано начальное условие
0
0
yy
xx
=
=
, то, определяя постоянную
C
, получим частное решение, удовлетворяющее данному условию.
Пример. Решить уравнение
dxx
y
dy
2
3=
.
Решение. Интегрируя обе части уравнения, получим:
⎮
⌡
⌠
⎮
⌡
⌠
= dxx
y
dy
2
3
, Cxy lnln
3
+= ,
3
x
eCy ⋅=
, – общее решение.
3
x
Cey =
Очень часто встречаются уравнения, в которых переменные еще не
разделены, но их можно разделить, производя простые арифметические дей-
ствия.
48
Определение. Дифференциальные уравнения, в которых переменные
можно разделить посредством умножения (деления) обеих частей уравнения
на одно и то же выражение, называется дифференциальным уравнением с
разделяющимися переменными.
Уравнение вида
)(
)(
1
2
yf
xf
dx
dy
=
приводятся к уравнению с разделяющимися переменными умножением обе-
их частей на . dxyf )(
1
Уравнение вида
0)()()()(
4321
=
+
dyyfxfdxyfxf
приводятся к уравнению с разделяющимися переменными делением обеих
частей на . При этом могут быть потеряны решения, обращающие
это произведение в нуль.
)()(
32
xfyf
Пример. Решить уравнение .
yyyx =+
′
1
22
Решение. Преобразуем уравнение:
1
22
−= y
dx
dy
yx , .
dxydyyx )1(
22
−=
Делим обе части уравнения на
: )1(
2
−yx
2
2
1
x
dx
dy
y
y
=
−
.
Переменные разделены. Интегрируем обе части уравнения:
⎮
⌡
⌠
⎮
⌡
⌠
=
−
2
2
1
x
dx
dy
y
y
,
⎮
⌡
⌠
=
⎮
⌡
⌠
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
++
2
1
1
1
x
dx
dx
y
y ,
C
x
yyy +−=−++
1
1ln
2
.
При делении на ) могли быть потеряны решения 1(
2
−yx 0=
x
и 01
=
−y (т.е.
). Очевидно,
0)1(
2
=−yx 1
=
y – решение уравнения, 0
=
x
– нет.
§ 4. Однородные дифференциальные уравнения 1-го порядка
Определение. Уравнение );( yxfy
=
′
называется однородным, если
функция );( y
x
f
может быть представлена как функция отношения своих ар-
гументов:
⎟
⎠
⎞
⎜
⎝
⎛
=
x
y
yxf ;
ϕ
)(.
Пример 1. Уравнение однородное, т.к.
его можно записать
0)2()(
2
=−−− dyxyxdxyxy
2
)(21
)(
2
2
2
2
xy
xyxy
xyx
yxy
dx
dy
−
−
=
−
−
= .

49
Однородное дифференциальное уравнение приводится к уравнению с
разделяющимися переменными заменой
x
t
y
⋅
=
( txy
=
), txty
+
⋅
′
=
′
.
Пример 2. Решить уравнение
xyx
yxy
y
2
2
2
−
−
=
′
.
Решение. Уравнение является однородным, т.к.
)(21
)(
2
xy
xyxy
y
−
−
=
′
.
Замена
x
t
y ⋅=
(
txy =
),
txty
+
⋅
′
=
′
приводит к уравнению:
t
tt
xtt
21
2
−
−
=⋅
′
+ ,
t
t
tt
x
dx
dt
−
−
−
=
21
2
, dx
t
tttt
xdt
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
+−−
=
21
2
22
, dx
t
t
xdt
21
2
−
= .
Разделяя переменные, получим
x
dx
dt
t
t
=
−
2
21
.
Интегрируем обе части полученного уравнения:
⎮
⌡
⌠
=
⎮
⌡
⌠
−
x
dx
dt
t
t
2
21
,
Cxt
t
lnlnln2
1
+−=+
,
x
C
t
t
lnln2
1
=+ ,
()
x
C
te
t
lnln
21
=⋅ ,
x
C
et
t
=⋅
12
, Ce
x
y
yx
=⋅
2
.
§ 5. Линейные уравнения 1-го порядка
Определение. Уравнение
)()( xqyxpy
=
+
′
, (1)
т.е. линейное относительно искомой функции и ее производной, называется
линейным. Здесь )(
x
p
и )(
x
q известные функции независимой переменной
x
.
Чтобы его решить, надо сначала решить уравнение
0)(
=
+
′
yxpy
(это делается путем разделения переменных) и в общем решении последнего
заменить произвольную постоянную
C
на неизвестную функцию )(
x
C
. За-
тем выражение, полученное для , подставить в уравнение (1) и найти функ-
цию
y
)(
x
C
.
Пример 1. Решить уравнение
2
2
x
xexyy
−
=+
′
.
Решение.
Решим уравнение 02
=
+
′
xyy : (*)
, xyy 2−=
′
xdx
y
dy
2−=
,
⎮
⌡
⌠
−=
⎮
⌡
⌠
xdx
y
dy
2,
Cxy +−=
2
ln ,
