Тимофеев В.А., Тимофеев А.А. Краткий курс лекций по высшей математике. Семестр II (сокращенная программа)
Подождите немного. Документ загружается.


30
)()( xfdttf
dx
d
x
a
=
⎮
⌡
⌠
.
Доказательство.
⎮
⌡
⌠
=Δ+
Δ+ xx
a
dttfxxJ )()(.
⎮
⌡
⌠
−
⎮
⌡
⌠
=−Δ+=Δ
Δ+ x
a
xx
a
dttfdttfxJxxJJ )()()()(.
Но
отсюда
⎮
⌡
⌠
+
⎮
⌡
⌠
=
⎮
⌡
⌠
Δ+Δ+ xx
x
x
a
xx
a
dttfdttfdttf )()()(, Jdttf
xx
x
Δ=
⎮
⌡
⌠
Δ+
)(.
По теореме о среднем значении
xcfdttf
xx
x
Δ⋅=
⎮
⌡
⌠
Δ+
)()(, где
x
x
c
x
Δ
+
≤
≤
.
Тогда
==
Δ
Δ
=
Δ
Δ
==
⎮
⌡
⌠
→Δ→Δ→Δ
)(lim
)(
limlim
)(
)(
000
cf
x
xcf
x
J
dx
xdJ
dttf
dx
d
xxx
x
a
)(
)()(lim)(
0
xf
xfcfянепрерывнаtf
xcxxxx
xc
=
=⇒−
→⇒→Δ+⇒→Δ
=
→
.
§ 5. Формула Ньютона-Лейбница
В предыдущем параграфе мы установили, что функция
является первообразной для непрерывной подынтегральной функции
⎮
⌡
⌠
=
x
a
dttfxJ )()(
( )
x
f
.
Как известно, всякая другая первообразная для функции )(
x
f
отличается от
)(
x
J
только постоянным слагаемым. Поэтому, если )(
x
F
– другая первооб-
разная для )(
x
f
, то
C
x
F
x
J
+
= )()(, или
CxFdttf
x
a
+=
⎮
⌡
⌠
)()(.

31
. Отсюда имеем: .
⎮
⌡
⌠
=
a
a
dttfaJ )()( )(0)()( aFCCaFdttf
a
a
−=⇒=+=
⎮
⌡
⌠
Значит,
)()()(
aFxFdttf
x
a
−=
⎮
⌡
⌠
.
В частности, при
b
x
= имеем:
)()()(
aFbFdttf
b
a
−=
⎮
⌡
⌠
– формула Ньютона-Лейбница.
Эта формула показывает, что, для того чтобы вычислить определенный
интеграл, нужно найти какую-либо первообразную )(
x
F
для подынтеграль-
ной функции )(
x
f
и взять разность ее значений в верхней и нижней грани-
цах интегрирования.
Пример.
6
0
6
0arcsin
2
1
arcsinarcsin
1
0
21
21
0
2
ππ
=−=−==
⎮
⌡
⌠
−
x
x
dx
.
§ 6. Замена переменной в определенном интеграле
Как и в случае неопределенного интеграла, вычисление определенного
интеграла можно упростить с помощью замены переменной.
Предположим, что нужно вычислить определенный интеграл
, где )
⎮
⌡
⌠
b
a
dxxf )(
(
x
f
– непрерывная на ]. Перейдем от переменной ;[ ba
x
к
переменой
t
, полагая )(
t
x
ϕ
= . Пусть
α
и
β
– числа, такие, что a
=
)(
α
ϕ
и
b=)(
β
ϕ
, и при этом выполняются условия:
1) )(
t
ϕ
и )(t
ϕ
′
– непрерывны на ];[
β
α
;
2) при изменении
t
от
α
до
β
значение функции )(
t
ϕ
не выходят за
пределы отрезка b
x
a
≤
≤
.
При этих условиях имеет место следующая формула замены переменной в
определенном интеграле:
⎮
⌡
⌠
′
=
⎮
⌡
⌠
β
α
ϕϕ
dtttfdxxf
b
a
)()]([)(.

32
Доказательство. Пусть )(
x
F
– первообразная для функции )(
x
f
, т.е.
. Тогда по формуле Ньютона-Лейбница )()( xfxF =
′
) . (*) ()()( aFbFdxxf
b
a
−=
⎮
⌡
⌠
Теперь покажем, что функция ))((
t
F
ϕ
будет первообразной для функции
)()]([ ttf
ϕ
ϕ
′
. Действительно:
)()]([)()(
)()())((
ttfxxf
d
t
dx
dx
xdF
d
t
xdF
d
t
tdF
ϕϕϕ
ϕ
′
⋅=
′
⋅=⋅== .
По формуле Ньютона-Лейбница имеем:
. (**) )()())(())(()()]([ aFbFFFdtttf −=−=
⎮
⌡
⌠
′
αϕβϕϕϕ
β
α
Из (*) и (**) следует, что
⎮
⌡
⌠
′
=
⎮
⌡
⌠
β
α
ϕϕ
dtttfdxxf
b
a
)()]([)(.
Пример.
=
⎮
⌡
⌠
−=
=⇒==⇒=
==
=
⎮
⌡
⌠
−
2
0
2
2
0
2
cos2sin44
22,00
cos2,sin2
4
π
π
dttt
txtx
tdtdxtx
dxx
π
π
π
π
π
=
⎥
⎦
⎤
⎢
⎣
⎡
−=
⎥
⎦
⎤
⎢
⎣
⎡
+=
⎮
⌡
⌠
+=
⎮
⌡
⌠
= 0
2
2
2
2sin
2)2cos1(2cos4
0
2
2
0
2
0
2
t
tdttdt .
§ 7. Интегрирование по частям в определенном интеграле
Пусть )(
x
uu = и )(
x
v
v
=
[
vdvu
– две функции, непрерывные вместе со свои-
ми первыми производными на . ]; ba
du
dxxuxvdxxvxu ⋅
′
⋅
+
⋅
′
⋅
vud ⋅ ][
=
⋅
+
⋅= )()()()( . (1)
Интегрируем тождество (1) в пределах от до b , получим a
. (2)
⎮
⌡
⌠
′
⋅+
⎮
⌡
⌠
′
⋅=
⎮
⌡
⌠
⋅
b
a
b
a
b
a
dxxuxvdxxvxuxvxud )()()()()]()([
По формуле Ньютона-Лейбница
a
b
b
a
xvxuxvxud )()()]()([ ⋅=
⎮
⌡
⌠
⋅ .

33
Тогда (2) примет вид
⎮
⌡
⌠
′
⋅+
⎮
⌡
⌠
′
⋅=⋅
b
a
b
a
a
b
dxxuxvdxxvxuxvxu )()()()()()(.
Откуда имеем
⎮
⌡
⌠
′
⋅−⋅=
⎮
⌡
⌠
′
⋅
b
a
a
b
b
a
dxxuxvxvxudxxvxu )()()()()()( . (3)
Формула (3) – формула интегрирования по частям в определенном интеграле.
Пример.
=
⎮
⌡
⌠
−+=
==
=+=
=
⎮
⌡
⌠
+
1
0
0
1
1
0
)1(
,
,,1
)1( dxeex
evdxedv
dxduxu
dxex
xx
xx
x
[]
eexeeex
xxx
=−==−+= 0)1(
0
1
0
1
.
§ 8. Вычисление площадей плоских фигур
с помощью определенного интеграла
8.1 Вычисление площади в Декартовых координатах
Рассмотрим следующие возможные случаи.
1. )(
x
f
определена и непрерывна на отрезке и 0];[ ba )( ≥
x
f
для любо-
го ];[ ba
x
∈ . В этом случае, как мы установили раньше, определенный
интеграл численно равен площади криволинейной трапеции
с основанием ], ограниченной сверху графиком функции
⎮
⌡
⌠
b
a
dxxf )(
;[ ba )(
x
f
.
Таким образом, мы получили формулу для нахождения площадей пло-
ских фигур следующего вида (рис. 5.2):
. (1)
⎮
⌡
⌠
=
b
a
dxxfS )(
Рис. 5.2
a
b
y
O
)(
y
f
x
=
x

34
2. Рассмотрим теперь фигуру, изображенную на рис. 5.3. Она представ-
ляет собой криволинейную трапецию с основанием ];[ ba , ограничен-
ную снизу графиком функции )(
x
f
. Таким образом, имеем )(
x
f
, оп-
ределенную и непрерывную на ];[ ba и 0)(
≤
x
f
для любого ];[ ba
x
∈
.
y
O
a
b
)(
y
f
)(
x
=
−
1
S
x
S
y
f
x
=
Рис. 5.3
Легко заметить, что площадь данной трапеции
S
будет равна площади
криволинейной трапеции с основанием ], ограниченной сверху гра-
фиком функции )
1
S ;[ ba
(
x
f
y −= (т.к. эти трапеции симметричны относительно оси
). Отсюда имеем: Ox
. (2)
⎮
⌡
⌠
−=
⎮
⌡
⌠
−=
a
b
a
dxxfdxxfS )()]([
b
Пример 1.
Найти площадь фигуры, ограниченной параболой и осью
2
xxy −=
O
x
.
Решение. Найдем точки пересечения параболы с осью O
x
:
или . 0)1(
,0
,
0
2
2
=⇒−=−⇒
⎩
⎨
⎧
=
−=
xxxxx
y
xxy
1
1
=x
Имеем криволинейную трапецию 1-го типа
(рис. 5.4):
6
1
3
1
2
1
32
)(
0
1
32
1
0
2
=−=−=
⎮
⌡
⌠
−
xx
dxxx
(кв.ед.).
Пример 2.
Найти площадь фигуры, ограниченной линями: 2−=
x
y , 0=
x
, 0
=
y .
0
1
y
1
x
Рис. 5.4
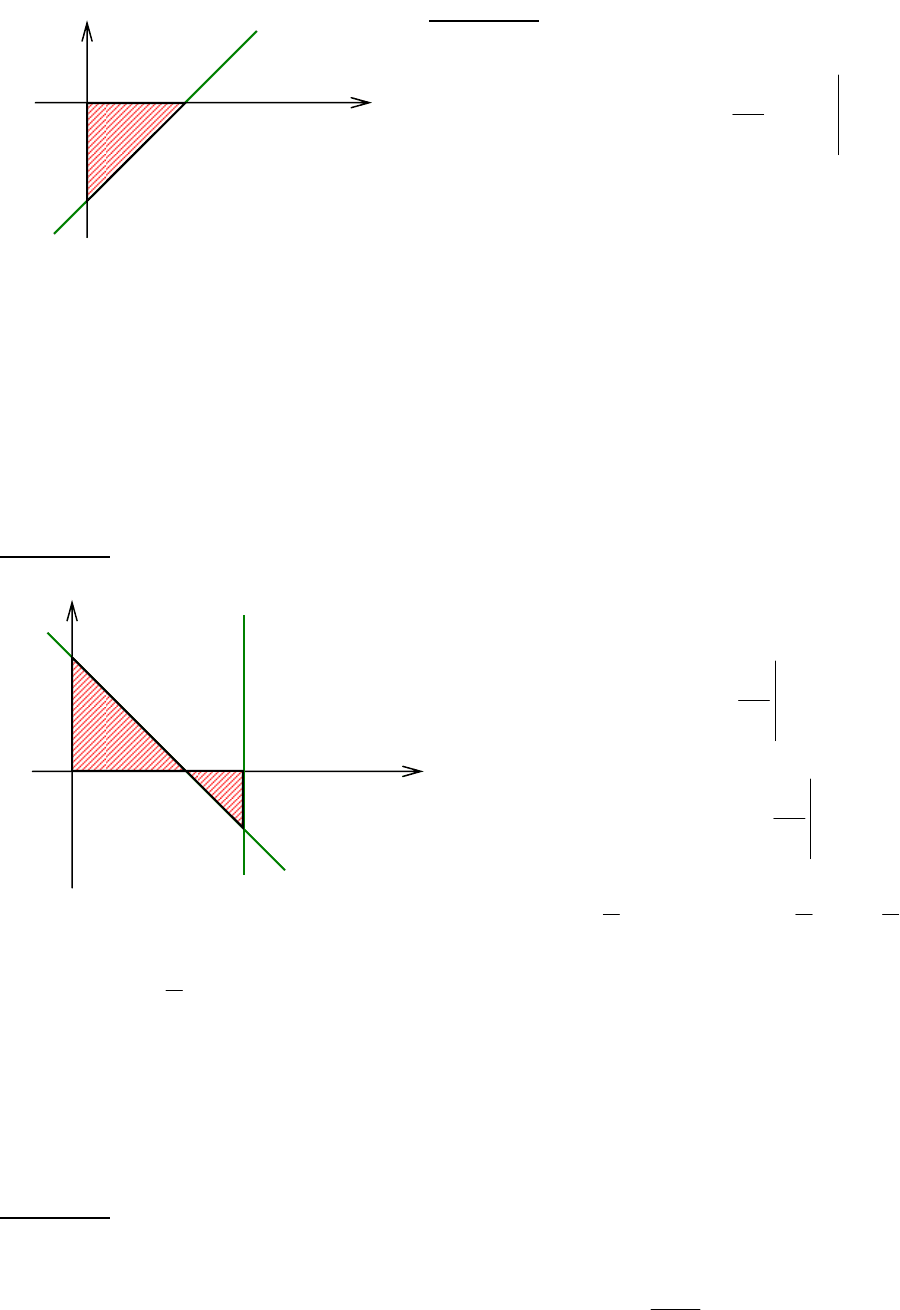
35
Решение. Имеем криволинейную трапе-
цию 2-го типа (рис. 5.5):
=
⎥
⎦
⎤
⎢
⎣
⎡
−−=
⎮
⌡
⌠
−−=
0
2
2
2
0
2
2
)2( x
x
dxxS
[
]
242
=
−
−
=
(кв.ед.).
Замечание. Все остальные плоские фигуры можно представить в виде раз-
личных комбинаций (объединений или дополнений) криволинейных трапе-
ций вида 1 или 2.
Пример 3.
Найти площадь фигуры, ограниченной линиями:
x
y −= 2, 0=
x
, 3
=
x
,
. 0
=y
Решение.
Искомая площадь равна (рис.5.6):
21
SSS +
=
.
224
2
2)2(
0
2
2
2
0
1
=−=−=
⎮
⌡
⌠
−=
x
xdxxS
.
=+−=
⎮
⌡
⌠
−−=
2
3
2
3
2
2
2
2)2(
x
xdxxS
2
1
2
2
3
)24(
2
9
6
=+−=+−−
⎟
⎠
⎞
⎜
⎝
⎛
+−=
.
Тогда
5,2
2
1
2 =+=S (кв.ед.).
Пример 4.
Вычислить площадь фигуры, ограниченной линиями ,
2
xy −=
02
=++ y
x
.
Решение. Найдем точки пересечения параболы с прямой
2
xy −=
02
=++ y
x
:
2,1,
2
31
,981,02
,2
,
212,1
2
2
=−=
±
==+==−−⇒
⎩
⎨
⎧
−−=
−=
xxxDxx
xy
xy
.
CBAODBADC
SSS −= (рис. 5.7).
Рис. 5.5
2
y
2
−=
y
O
x
x
2−
y
2
O
Рис. 5.6
3
x
x
y −= 2
3
=
x
1
S
2
S
36
=+=
⎮
⌡
⌠
−−−=
−
−
1
2
2
2
1
2
2
]2[ x
x
dxxS
BADC
y
5,75,16]25,0[]42[ =+=
−
−
+
=
.
3
3
1
3
8
3
1
2
3
2
1
2
=+==
⎮
⌡
⌠
−−=
−
−
x
xS
CBAOD
.
5,435,7
=
−
=
S
(кв.ед.).
3. Фигура представляет собой криволинейную трапецию с основанием
];[
ba , ограниченную сверху кривой )(
t
x
x
=
, )(
t
y= , где )(y
t
x
, )(tx
′
,
)(
t
y – непрерывные функции на ];[
β
α
( a
x
=
)(
α
, b
x
=)(
β
). В соот-
ветствии с п.1 имеем:
⎮
⌡
⌠
′
=
→→=
′
==
=
⎮
⌡
⌠
=
β
α
βα
dttxty
batyy
dttxdxtxx
dxxfS
b
a
)()(
,),(
,)(),(
)( . (3)
Получили формулу для вычисления площади криволинейной трапеции,
когда кривая задана параметрическими уравнениями.
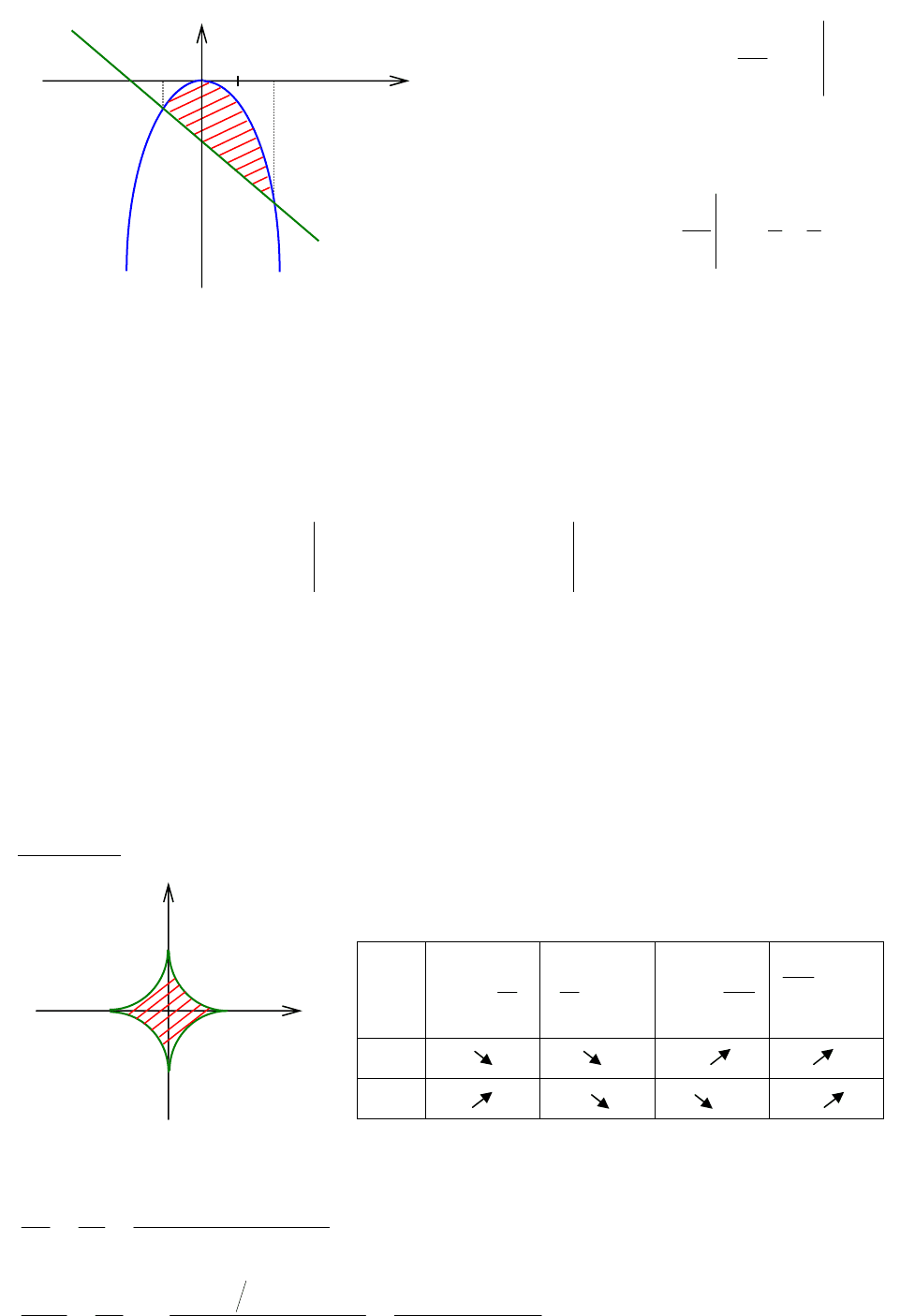
Пример 5.
Вычислить площадь фигуры, ограниченной линией
t
a
x
3
cos
=
,
(
tay
3
sin=
0>= cons
t
a ).
Решение. Анализ данной линии представлен в таблице 1. Искомая площадь
изображена на рис. 5.8.
)( tg
)sin(cos3
cossin3
2
2
tgt
tta
tta
x
y
dx
dy
t
t
=−=
−⋅⋅
⋅⋅
=
′
′
=
;
⎩
⎨
⎧
<<<
<<>
=
⋅
=
−⋅⋅
−=
′
′
=
.2,0
,0,0
sincos3
1
)sin(cos3
cos1
42
2
2
2
ππ
π
tесли
tесли
ttatta
t
x
g
dx
yd
t
t
Рис. 5.8
x
y
a
−
a−
a
a
Таблица 1
t
2
0
π
→
π
π
→
2
2
3
π
π
→
π
π
2
2
3
→
x
a 0 0 a
−
a− 0 0 a
y
0
a a 0 0 − a a
−
0
Рис. 5.7
B
C
x
A
D
2
4
−
2
xy −=
2
y
O
x
=
−
−

37
=
⎮
⌡
⌠
−⋅⋅=
⎮
⌡
⌠
′
⋅==
0
2
23
0
2
1
)sin(cos3sin4)()(44
π
π
dtttatadttxtySS
=
⎮
⌡
⌠
⋅⋅=
⎮
⌡
⌠
⋅=
2
0
2222
2
0
242
cossinsin12cossin12
ππ
dttttadttta
Jdtttdttadt
tt
a =
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⎮
⌡
⌠
−
⎮
⌡
⌠
=⋅
⎮
⌡
⌠
−
=
2
0
2
2
0
22
2
2
0
2
2cos2sin2sin
2
3
4
2sin
2
2cos1
12
ππ
π
.
[]
44
4sin
2
1
4cos1
2
1
2sin
0
2
2
0
2
0
2
π
π
π
π
=
⎥
⎦
⎤
⎢
⎣
⎡
−=
⎮
⌡
⌠
−=
⎮
⌡
⌠
t
tdttdtt .
0
2
1
02,00
,22cos,sin
2cos2sin
0
0
2
2
0
2
=
⎮
⌡
⌠
=
=⇒==⇒=
⋅==
=
⎮
⌡
⌠
duu
utut
dttdutu
dttt
π
π
.
8
3
42
3
2
2
a
aJ =⋅=
π
(кв.ед.).
8.2 Вычисление площади в полярных координатах
Пусть дан криволинейный сектор , ограниченный радиусами-
векторами и , и кривой, уравнение которой задано в полярных коор-
динатах )
OAB
OA OB
(
ϕ
ρ
ρ
=
(рис. 5.9). При
этом предположим, что )(
ϕ
ρ
не-
прерывная на ];[
β
α
функция.
Рис. 5.9
B
Пусть радиус-вектор об-
разует с осью
OA
l
угол
α
, а радиус-
вектор OB – угол
β
. Разобьем угол
на части с помощью лучей,
выходящих из полюса и обра-
зующих с полярной осью углы:
OAB
O
β
ϕ
ϕ
ϕ
α
<
<<
<
<
−121 n
K ;
обозначим
α
ϕ
=
0
и
β
ϕ
=
n
.
Обозначим точки пересечения лучей с кривой через , , …, . Криво-
линейный сектор разобьется на малых криволинейных секторов
, , …, . Углы , , …, соответственно
равны
1
A
A
n
2
A
OB
1
1
−n
A
OAB
A
n 1−
0
n
A
1
AOA
21
OAA
1
OB
1
AOA
21
OA
−
1
ϕ
ϕ
ϕ
−=Δ ,
122
ϕ
ϕ
ϕ
−
=
Δ , …,
1−
−
=
Δ
nnn
ϕ
ϕ
ϕ
. Если обозначить че-
β
α
i
ϕ
~
O
l
A
1−i
A
i
A
i
M

38
рез
S
площадь всего криволинейного сектора, а через
i
S
Δ
– площадь малого
криволинейного сектора, ограниченного лучами и , то
1−i
OA
i
OA
. (4)
∑
=
Δ=
n
i
i
SS
1
Далее поступим следующим образом. Внутри каждого малого сектора
проведем луч под углом
ii
A
− i
ϕ
~
(OA
1 i
ϕ
ii
ϕ
ϕ
<
<
−
~
1
i
OM
). Точку пересечения этого
луча с кривой обозначим через . Тогда
i
M
ii
ρ
ϕ
ρ
=
=
)
~
( . Заменим теперь
каждый малый криволинейный сектор круговым сектором с центром
в точке радиуса
ii
OAA
1−
O
i
ρ
. Площадь каждого такого кругового сектора равна
ii
Δ
2
ϕρ
2
1
и дает приближенное значение площади соответствующего криво-
линейного сектора. Таким образом, имеем
i
ϕ
i
ρ
Δ
2
i
S ≈Δ
2
1
. Тогда
∑
=
Δ≈
n
i
ii
S
1
2
2
1
ϕρ
. (5)
Точность этого приближенного равенства повышается с уменьшением
i
ϕ
Δ
.
Поэтому точное значение площади
S
криволинейного сектора получится как
предел площади фигуры, составленной из круговых секторов, при условии,
что все
0→Δ
i
ϕ
. Таким образом,
∑
=
→Δ
Δ=
n
i
ii
i
S
1
2
0
2
1
lim
ϕρ
ϕ
.
Т.к. правая часть (5) есть интегральная сумма для непрерывной функции
)(
2
2
1
ϕρ
, то ее предел есть определенный интеграл, т.е.
⎮
⌡
⌠
=
β
α
ϕϕρ
dS )(
2
1
2
. (6)
Пример 6.
Вычислить площадь фигуры, ограниченной линиями
ϕ
ρ
cos2= , 1
=
ρ
(вне круга 1=
ρ
).
Решение.
Линия
ϕ
ρ
cos2= представляет собой “однолепестковую розу”
(
220cos0
π
ϕ
π
ϕ
ρ
≤
≤−≥⇒≥ ⇒ );
линия 1
=
ρ
– окружность радиуса 1 с цен-
тром в полюсе (рис. 5.10). Найдем точки пе-
ресечения линий:
Рис. 5.10
O
2
3
π
1
l
3
1cos
ϕ
2
,1
,cos2
π
ϕ
ρ
ρ
ϕ
±=⇒⇒
⎩
⎨
⎧
=
=
=
.
Искомая площадь равна .
секл
SS −S =
3−
π

39
=
⎥
⎦
⎤
⎢
⎣
⎡
+=
⎮
⌡
⌠
+=
⎮
⌡
⌠
=
⎮
⌡
⌠
=
−
−
−−
3
3
3
3
3
3
2
3
3
2
2
2sin
]2cos1[cos2
2
1
π
π
π
π
π
π
π
π
ϕ
ϕϕϕϕϕϕρ
dddS
л
2
3
3
2
4
3
34
3
3
+=
⎥
⎦
⎤
⎢
⎣
⎡
−−−
⎥
⎦
⎤
⎢
⎣
⎡
+=
πππ
.
33
2
1
2
1
2
1
2
π
π
ϕ
=⋅⋅== rS
сек
.
Тогда
2
3
332
3
3
2
+=−+=
πππ
S (кв.ед.).
§ 9. Длина дуги плоской кривой
9.1 Вычисление длины дуги в Декартовых координатах
Теорема. Пусть кривая
∪
A
B задана уравнением )(
x
f
y = , где )(
x
f
–
непрерывная функция, имеющая непрерывную на ] производную. Тогда
дуга
;[ ba
∪
A
B имеет длину, равную
b
[]
dxxfl
a
⎮
⌡
⌠
′
+=
2
)(1
. (1)
Доказательство.
Разобьем дугу
∪
A
B точками , , …, на частей.
Обозначим абсциссы этих точек через , , …, . Имеем
1
M
x
2
M
1−n
1−n
M
n
1
x
2
x
bxxxxax
nn
=
<
<
<
<
<
=
−1210
... .
Построим ломаную . Длина ломаной будет равна BMMMA
n 121
...
−
∑
=
Δ=
n
i
LL
1
1
, где
i
L
Δ
– длина -го звена . i
ii
MM
1−
2
1
2
1
2
1
2
1
))()(()()()(
−−−−
−+−=−+−=Δ
iiiiiiiii
xfxfxxyyxxL
.
По теореме Лагранжа:
)()()()(
11 −−
−
⋅
′
=−
iiiii
xxcfxfxf , где
iii
xcx
<
<
−1
.
Обозначим
1−
−
=
Δ
iii
xxx . Тогда имеем
[][]
iiiiii
xcfxcfxL Δ⋅
′
+=Δ⋅
′
+Δ=Δ
22
2
)(1)(.
Отсюда длина ломаной
L
будет равна
[]
∑
=
Δ⋅
′
+=
n
i
ii
xcfL
1
2
)(1 . (2)
