Тевяшев А.Д., Литвин О.Г. Вища математика у прикладах та задачах. Ч 1
Подождите немного. Документ загружается.


Глава 4
521
Е
3
= І0,-|,0,0,1 ] , с
ь
с
2
,с
3
єК. 3.146. (1,-1,-1,1)
т
.
3.147. (6 - с, - 5 + с, 3, -1 - с, с)
т
, с є К . 3.148. Система несумісна.
(5 3 116
3
*
149
* [ 2 ~ 2
Сі
'
Сі
'°'°'у
_
з
с
2.
с
2 І
>
с
ь
с
2
єК .
3.150. (-1 +
С]
+ 2с
2
, - 3 +
С\
+ 2с
2
, Сі, с
2
)
Т
, С],с
2
є К .
Глава 4
4.4.
Так, якщо пряма проходить через початок координат. 4.5. Ні
'-1 0 0
Л
4.7.7р_>
р
.= 0-1 0
0 0-1
ґ
1 1 -1> ( 1/2
Ч
4.6. Тр^р =
1 -1 2 -3/2
,о о -і
у
1 -у
Го 0 г
'~
2
)
2
• 4.8.
г
р->р' -
і 0 0
, х'
=
1
• 4.8.
г
р->р' -
,о
1
о;
, 1
. 4.9. а) Так; б) так; в) ні;
г) ні. 4.10. а) Так; б) ні; в) так. 4.11. а) Так; б) ні; в) так; г) ні; д) так.
4.12.
г = 2; базисом є, наприклад, система х
2
).
4.13.
7^
( 1
2 1 0
2
3 2
3
, х'
=
2
, х'
=
-1 0 1 -1 1
,-2
-1 4
о,
А
. 4.14. а)
б)
ґ
0
Л
-2
1
V «У
4.16. 0
. 4.17.
1
,-1у
11
4.18. а) Так; б) так; в) ні; г) ні; д) ні. 4.19. а) Так;
б) ні; в) ні; г)так; д) ні. 4.20. а) 1,(і, 7, 5); б) 3,
(-0,1;
0,7; 1; 0; 0),
(-0,4;-0,2; 0; 1; 0), (0,4; 0,2; 0; 0; 1). 4.21. а) (3, -2, 5 ),

522
Відповіді
б) (0,4,-1), в) (4,12,9). 4.22. а) (-1,5,2,і), б) (3, 7,-4, 12).
Гі
1
4.23.
2
. 4.24.
1
,1
4.25.
2
1
. 4.26. а), б) Підпростір вимірності 2,
базисом є будь-яка пара неколінеарних векторів з заданої множини; в) не
є підпростором. 4.27. а) Підпростір вимірності я - 2 , б) не є підпростором.
4.28. Множини, вказані у пп. а) ,б), г) - підпростори, а множина з в) не є
підпростором • Умову, якій задовольняють координати у будь-якій задачі
з цієї серії, можна записати у вигляді А X = 0, де А - деяка матриця, що
має п стовпців, а X - стовпець координат у фіксованому базисі. Отже,
вимірність відповідного підпростору дорівнює п - К§ А , а за базис можна
узяти будь-яку фундаментальну систему розв'язків системи рівнянь
АХ = 0. 4.29. а) Підпростір вимірності п
2
-С
2
=- ; б) не є
підпростором. 4.30.2. 4.31.3; один з базисів є, наприклад, р = (х
х
, х
2
, х
4
).
4.32.
3; один з базисів є, наприклад, р = (х
х
, х
2
. *5 )• 4.33. а) | х | =
л[Е
,
|у| = 3, (х, у) = 3, сов
ф = -А
;
б)
|
х
|
= л/ЇО , |
V |
= л/? , (х, у)=2,
со5ф
= ;в)|х| =
13,
|у| = л/і4, (х, у)=-15, со8ф = ==.
4.34. а)
б)
1
\
0,
л/и
'
л/І4
'
Ти
і'
1.
'л/Гз'
л/ІЗ
2 3_1 ( 1 5 3_
л/35 '
л/зТ
л/35
_гз_
/І82
:
л/Ї4 ' л/Ї4 ' л/Ї4 ^ '
в) (і, 0, 0)
/182
З
182
л/ЇО
, 0,
< 1 1
Л
0 —— ——
л/2' лЯ
0,
1
л/2 ' л/2.
. 4.35. а)
0, 0,
л/2'
л/2
-7=,
-^=, 0, 0
лЯ л/2
(
1 1
Л
0, о, —і,
л/2 л/2

Глава
5
523
б)
ґ
±_
0
_1_ _2_) ( л/з~
п
л/з~ л/Р
ґ
л/б'
' л/б' л/б
0, --і-,
V
З
3 3
о,
о
л/2
л/2
(0,1,0,0).
4.36.
/!=!,=(!,
1, 1, 1),
/
2
=(2,2,-2,-2),
7
3
=(-1,
1,
-1,1).
4.37. /,
=£,=(1,2,1,3),
/
2
=
10
З
з
7
3=
[_І9.,ІІ,^.,_І2.). 4.38. 7, =я,
=(1,2, 2,-1),
У3
у
185 185 185
185
) ^ *і V . . л
7
2
=(2,з,-з,2), /,=(2,-1,-1,-2).
4.39.
р=(7,,7
2
,7
3
),
/,=(1,2,2,-1), /
2
=(2,3,-3,2), /з=(2,-1,-1,-2).
4.40.
Р=(/,,/
2
.Л).
/,=(2,1,3,-1),
7
2
=(3, 2,-3,-1),
/з=(і,5,1,10).
4.41.
е
3
=(-4,
2,
-1,
3),
е
4
=(2,4,3,1).
Для
визначення вектора
е
3
= (х
х
, х
2
, х
3
, х
4
)
достатньо знайти який-небудь
РОЗВ'ЯЗОК
СИСТеМИ
ВІДНОСНО НеВІДОМИХ
Х| , х
2
, х
3
, х
4
двох лінійних
рівнянь
(Є3,
Є]
) =
0,
(?з,е
2
)=0.
Для
визначення
е
4
аналогічна
система скла-дається
з
трьох рівнянь.
4.42. е
4
=(і,-1, 1,-1,
0),
е
5
=(0,5,1,-4,-2).
4.43. 4.44.
<?
3
=(і,-2,
1, 0),
£,=(25,4,-17,-6).
4.45. а) -1 + 6/;
6)2-4/.
4.46. а)
91
+
63/,
|5|
=
л/Ї57
, |б| =
л/Ї06
; б) 4-4/, |й| =
|й|
=
л/б
.
Глава
5
5.1.
Є
лінійним оператором;
А =
оператором.
5.3. Є
лінійним оператором; якщо
<5
= а, / + а
2
у + а
3
&
, то
А
0 0
одо
0
0 Я
5.2.
Не є
лінійним

524
Відповіді
0 - «з «2
«З 0 -Я]
{-а
2
щ 0
. 5.4. Не є лінійним оператором. 5.5. Є лінійним
оператором; А-
Го і її
2 0 1
3 -1 1
V
5.6. Є лінійним оператором;
0 1 1
2 0 1
3
-1 1
А =
оператором;
5.7. Не є лінійним оператором. 5.8. Є лінійним
ґ
0' 0 0"|
0 1 -1
)
V
0 0 0
5.9. Є лінійним оператором;
А =
1 2 2
0 -3 1
,2 0 3^
5.11. Не є лінійним оператором.
5.10.Є
лінійним оператором; А-
1 0
1 -2 -1
0 3 2
5.12. С =
5.13. с =
' 22 13 - 37^
-39 -16 25
- 1 0-6
Сх = (22х] + 13х
2
~37хз ,
-39X]
-16х
2
+ 25х
3
,
-X]
- 6х
3
)
-15 23 -7^
2 8-4
-7 1 7
С х = (-15 X] + 23 Х2 -
7
хз,
2х} +8х
2
-4х
3
, -7х{ +х
2
+7х
3
).
5.14. С = 0, Сх = 0. 5.15. С =
2 3-2
1 0 -4
5 0-2
Сх = (2хі +3х
2
-2х
3
,
Хі -4х
3
, 5х
(
-2х
3
) .
П 2 П
Г-6 6 зї
'1 14 5'
5.16. а) 5 3 0
; б)
13 6 2
; в)
8 -8 -2
12 7 6,
,20
ч
7
23
]
К
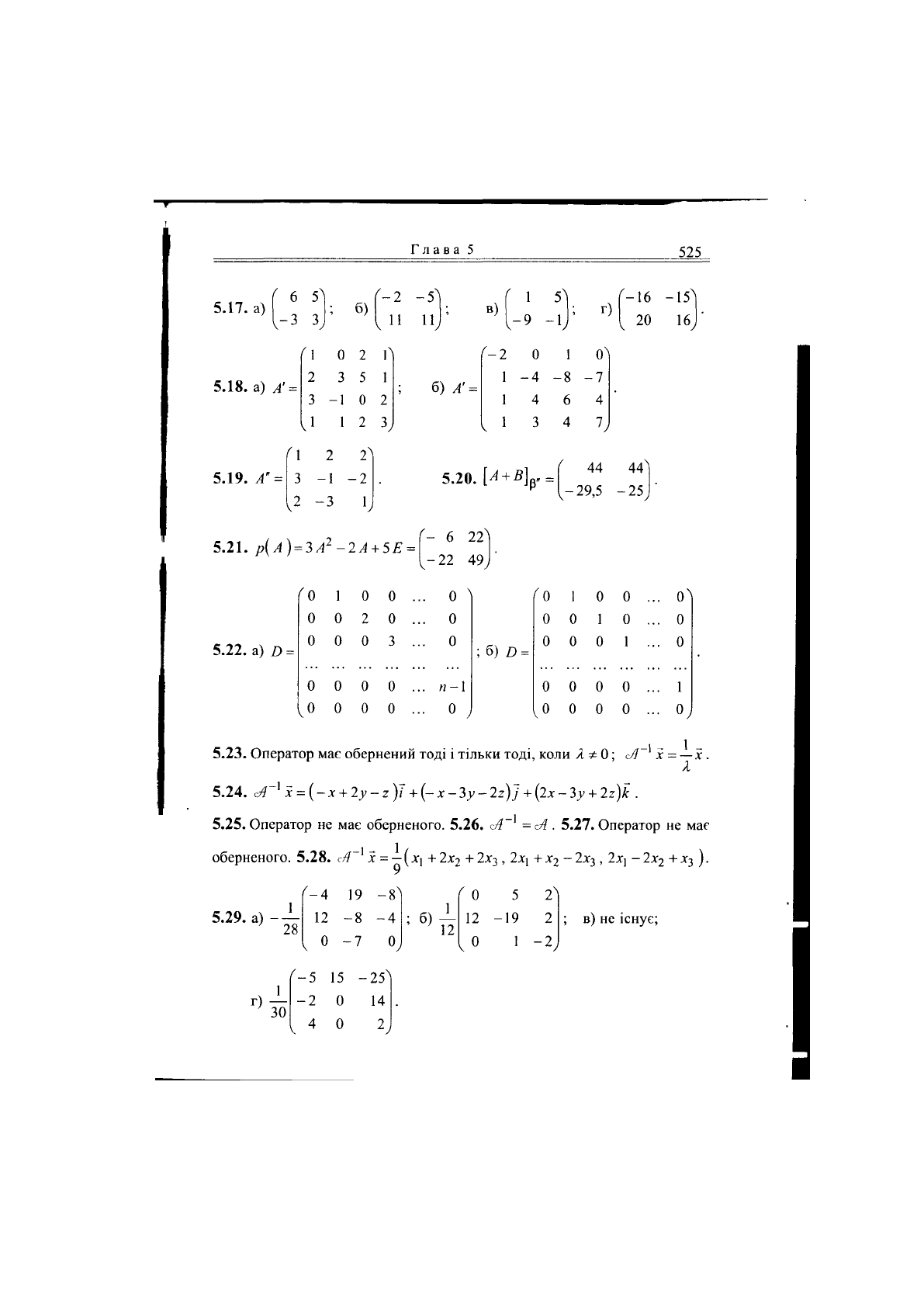
Глава 5
525
5.17. а)
6 5
-З З
б)
'-2 -5
Л
ч
11 11
в)
-9
-І
г)
Г-16 -15
Л
20 16
5.18. а) А' =
(\ 0 2
0
2 3 5
1
;
б)л' =
;
б)л' =
3 -1 0 2
;
б)л' =
чі 1
2
з,
V
2 0 1 0І
1 -4 -8 -7
14 6 4
13 4 7
5.19. А" =
1 2
З -1
2 -З
2^
-2
1
5.20. И + Д]
р
.=
44 44
-29,5 -25
5.21.
р(А)
=
ЗА
2
-2А + 5Е =
ґ
-
6 22
Л
-22 49
Го 1 0
0 .
..
0
4
Го 1
0 0 .
.
0
0 0
2 0 .
..
0
0
0 1 0 .
.
0
5.22. а) О =
0 0 0
3 .
.
0
;
б) о =
0 0
0 1 .
.
0
0 0
0
0 .
.
л-1 0 0
0 0 .
.
1
0
0
0 . 0
0 0 .
.
0
5.23. Оператор має обернений тоді і тільки тоді, коли Л^О; Л
1
х =
—
х.
5.24. Л~
]
х = (-х +
2у-г)ї
+
(-х-Зу-2г)]
+ (2х-Зу + 2г)к .
5.25. Оператор не має оберненого. 5.26. <А
_І
= сА . 5.27. Оператор не має
оберненого. 5.28. х. = (х, + 2х
2
+ 2х
3
, 2х
х
+х
2
- 2х
3
, 2х. - 2х
2
+ х
3
).
5.29. а) - —
28
-4 19 -8
12 -8 -4
0-7 0
;
б) —
12
0
12
0
5 2
Л
-19 2
1 -2
в) не існує;
г) —
30
Г-5
15 -25^
2 0 14
4 0 2

526
Відповіді
5.30. аіт ІтА = 2; базис
1т
А :
Є]=(2,1,і),
с
2
=(-1,-2, 1);
штКегс^ = 1; базис Кетаі: е = (\, 1, і).
5.31. штітс^ = 1; базис Ітої: е=(і,1,і);
аітКегс4=2;базис Кег А: ^=(1,-1,0), е
2
=(і,0,-і).
5.32. а) КегсЯ = {0}, Іт^=К
3
,
К§с/?
= 3, &{Л = 0;
б) КегЛ =
{с(-1,
7, 4)| Ус є К},
Іт
с
т?
= {с,(і,3,4)+с
2
(-1,1,0)|Ус,,с
2
єй),
К§гУ?
= 2, аеґс^ = 1;
в) Кегс4 = {{с
х
, -4с, -2с
2
,с
2
)
\
Ус,, с
2
є К };
Ішсі
=
{с(4,1,
2)|
УсєК},
К§с^=1,
аеГс^=2;
г)
Кег<^ = К
3
, Ітст? = {0},
К§с^
=0, аеГс//=3.
5.33. Кегс^ : сукупність многочленів нульового степеня, тобто констант;
аіт Кег
сй
= 1;
Іт с4 : сукупність многочленів, степінь яких < п - 2 ; аіт ІтЛ
=
п -1.
5.34. а) х
2
, х
3
- власні вектори з власними значеннями А
х
= 3 , А
2
= 2
відповідно; б) х
х
- власний вектор з власним значенням Я] = -3 ;
в)
X],
х
2
- власні вектори з власними значеннями А
х
= 1, Л
2
= 5
відповідно.
5.35. а) А
2
-51 + 6 = 0; спектр: 2, 3; б) А
2
-61+ 8 = 0 ; спектр: 2, 4;
в) Д(Д-2)(Д-3) = 0; спектр: 0, 2, 3; г) (Л-1 )
2
( А + 3 )= 0 ; спектр:-З,
1,1; д) (Я-4)
2
(Я-5)=0; спектр: 4, 4, 5; е) (Я-1 )
2
( А-2 )(Я +1 )= 0;
спектр: -1, 1, 1, 2; є) (А-4)
2
(Д-1 )
2
= 0 ; спектр: 1, 1, 4, 4;
ж) (Л-9)
2
(Д-і)(Л + і) = 0; спектр: -1, 1,9, 9.
5.36. Л =
-1,
х(
л
)=с(і,1,-і), сєК, с*0.
5.37. А = 2, х^ = с\{\, 2, 0)+с
2
(0, 0, і), с
х
, с
2
є К , Іс, | + |с
2
І
^ 0 .

Глава 5
527
5.38./^=1,
*(
Я|
) = с(і, 1, і); Я
2
=0,
х
(
Л
А = с(і, 2, 3), сеК, с*0.
5.39. Я = 1, Зс(
Л
)=с(3,1,і). сєК, с*0.
5.40. Я, = 3,
х^=с{\,
2, 2); Я
2
=-1, х^
2
' = с(і, 2,і),сєК,с*0.
5.41. Я, =1, )=сі(2, 1, 0)+с
2
(і, 0, -і), с,, с
2
єК, |
Сі
| + |с
2
|*0;
Я
2
=-1,
х^
2
' = с(3, 5, б), сєК, с*0.
5.42. Я, = 2, )=с(0,1, 0); Я
2
=1, х^
2
)=с(0,
1,-і),сєК,с*0.
5.43. Я =
-1,
х(
д
)=с
1
(5, 0, і)+с
2
(-2, 1, 0), с,, с
2
є К , |с,
|
+ |с
2
| * 0 .
5.44.
Я-=-1,
х
(Д|
) = с(і, 1, і); Я
2
=2, х^
2
)
= с
(
4> 7
).
Я
3
=-2,
х(
Дз
' = с(2,3,3); сєК, с#0.
5.45. Я = 2, х'
д
)=с(2,-4, 3), сєК, с#0.
5.46. Я
1>2
=1 + 3/, х^
1
) = с(і,-/), х^
2
)=с(і,/), сеС, с*0.
5.47. Л
И 2
=±3/, х^')=с(5,
1-3/),
х*
Д2
'=с(5,
1
+ 3/), сєС, с*0.
5.48. Я] = 2, Я
23
=3±/, х(
Д|
^
= с(і, 0, і), сєК, с*0;
х^
=
с{\,
1
+ /, 2-/), сєС, с*0;
х^
3
^ = с(і, 1-/, 2 +
/),
сєС, с*0.
5.49. Я, =-2, Я
23
=+4/, х(
я
') =
с
(-4, 1, і), сєК, с*0;
х(
Д2
)=с(2,/,2), х^
3
^ = с(2,-/, 2), сєС, с*0.
£=(1,0, 0, 0); (\ 0 0 0^ £=(1, 1, 1, і);
б^І
0
'
2
'"
1
'
°^=°
1 0 0
.5.51.
-
2
-0'-і,
і, -і);
е
3
=( 1, 1, 0, 0); 0 0 2 0 е
3
=(і, 2,4, 8);
е
4
=( 1, 0, 2,-і), [о 0 0 2) е
4
=(і,-3, 9,-27),

528
Відповіді
0
0
0
0 0
-1 о
0 2
0^
0
о
еі=(і,
і, О;
5.52. е*
2
=( 1, 0, -і);
*$=(о,
1,-1),
0 0 -3^
5.53. Не зводиться до діагонального вигляду.
?!=(!,
0,-1); ("О 0 0^
3 0 0
0 0 0
0 0 0
5.54. е
2
={ 1, 0, і);
£>
=
^=(0,1,
0),
0 1 0
0 0 1
Є|=(
1,0,-3);
5.55. є
2
=(0, 1, 3);
г
3
=(і,
1, О,
Г2 0 0
Л
0 2 0
0 0 1
V
Є|=(і,
1, 0, 0);
5.56. ^ °'
1
' °]
;
е
3
=(і. 0, 0, і);
е
4
=(і,-1,-1,-і),
^2 0 0 0^
0 2 0 0
0 0 2 0
0 0 0 2
5.57,
є, =( 1, 0,0, і);
е
2
=( 0, 1, 1,0);
е
3
=(
0,-1,1,0);
е
4
=(-1,
0,0,1),
1
0 0 0
0
1
0 0
0
0
-1
0
0 0 0
-\
е
\ =
5.58. е
2
=
е
3
=
2 2 І
3 ' 3 ' З
І _
2
І
з' з'
З
2
з
!
і
2
з'
з
£> =
'9 0 0~
0-9 0
0 0 18
5.59. е
2
=
5
3
=
1 1
VI'
VI
і
5.60. е
2
=
VI
VI
і
VI'
VI
е
3
=(
0, 0
, о
),
1
1
о
л/ЙГ
л/Ї8' л/Ї8
9 0 0^
0 9 0
0 0 27
(
'2 0 ОЇ
0 4 0
0 0 4
5.61. е
2
=
1 1
\
0
Чл/І'
VI' У
'і 1 1
Л
л/з'
VI'
VI
_1_
_2_ _2_
л/б'
л/б' л/6
5
3 =
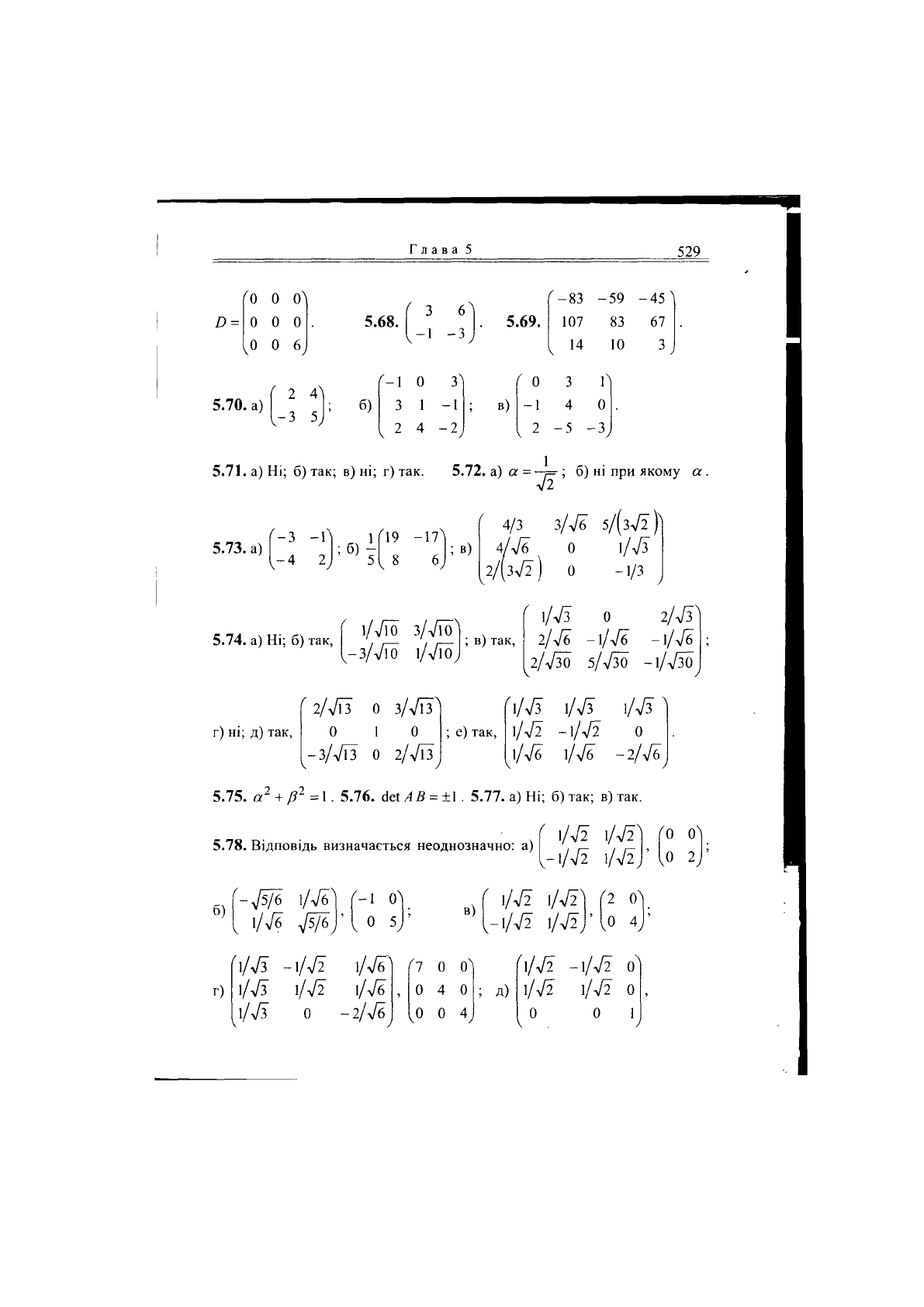
Глава 5
529
О
О (Л
ООО
0 0 6
5.70. а)
2 4
-З
5
5.68.
( 3 6
-1 -З
б)
-10 3"|
З
1 -1
2 4-2
5.69.
в)
-83 -59 -45
107
83 67
14 10 3
3 О
-14 0
2 -5 -З
5.71.
а) Ні; б) так; в) ні; г) так. 5.72. а) а = -4=-; б) ні при якому а.
л/2
5.73.
а)
ґ-3 -А і
4 2
;б)
7
Гі9 -\І
; в)
4/3
3/л/б
5І(зЛ)
4/Уб
0 і/л/з
2/(зл/2")
0 -1/3
5.74. а) Ні; б) так,
і/л/їо з/л/То
-з/л/їо і/л/Го
в) так,
і/л/з 0 2/л/з
2/7б
-і/л/б -і/л/б
2/л/30 5/л/30
-і/л/зО
г) ні; д) так,
2/л/ЇЗ
о
з/л/їз
0 1 О
-З/л/ЇЗ
0
2/л/ЇЗ
; е) так,
1/л/з"
і/л/3"
1/л/з"!
і/л/2 -і/л/2 О
і/л/б і/л/б -2/7б
5.75. се
2
+ /9
2
= 1. 5.76. оеі А В
=
±1 . 5.77. а) Ні; б) так; в) гак.
5.78. Відповідь визначається неоднозначно: а)
і/л/2"
1/л/Г
і/л/2 і/лЯ
О
О
ч
0 2
)
б)
'-л/5/6
1/л^І
/
1
1/^
V
-1 о
0 5
в)
Г іА/2
і/72"1
/
1-1/72"
і/^
V
2 0
О
4
г)
і/л/3 -і/л/2
і/л/б'
і/л/3 і/VI і/л/б
і/л/з 0
-2/л/б
\
Ґ7 0
о
4
ш
-і/Л о
л
0 4 0
; д)
і/л/2 0
/
,о
0
Ь
0
V.
0 1
)
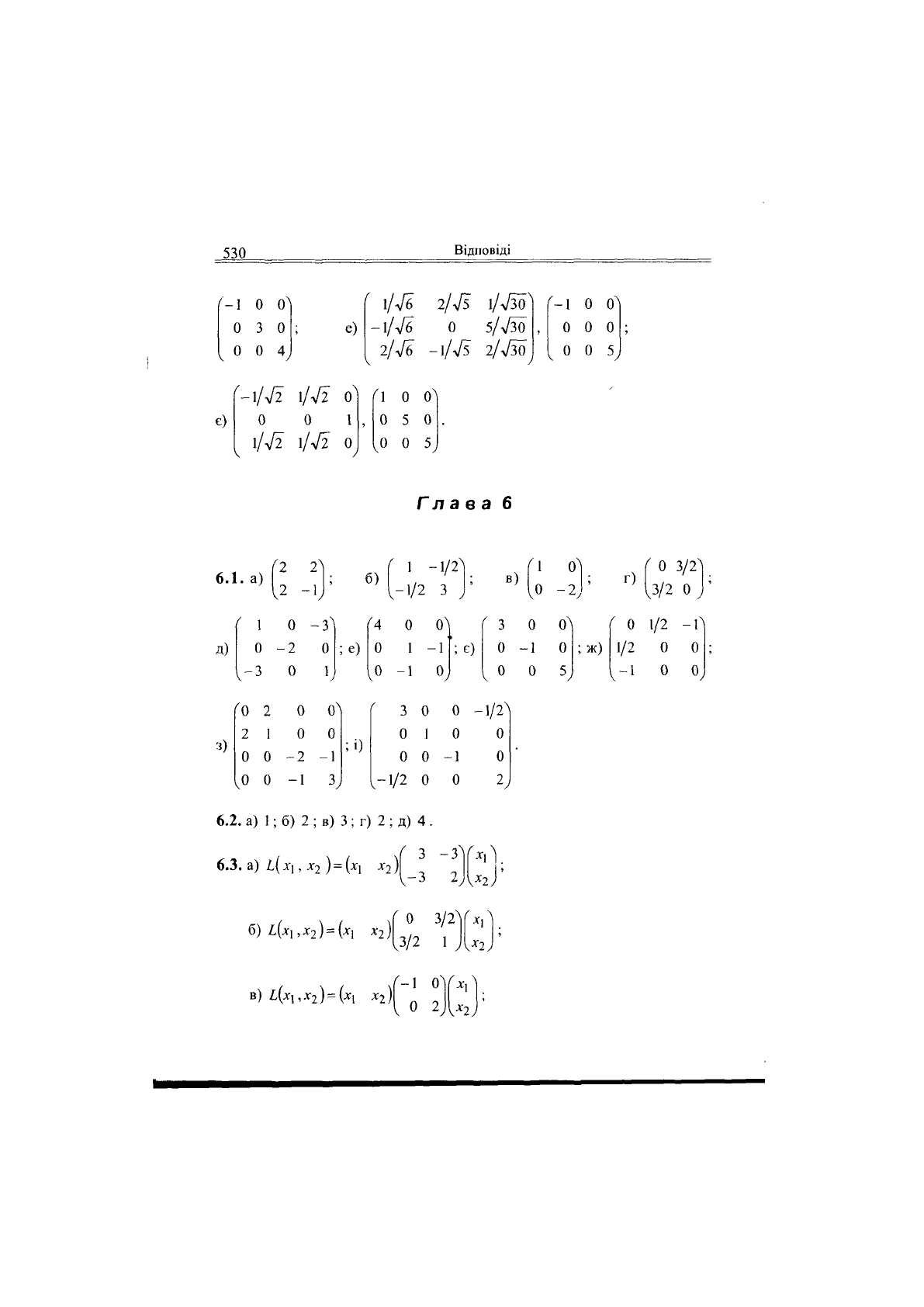
530
Відповіді
г-1
0 0^
і
0
3
0
;
е)
0
V
V
є)
-1/Тб 0 5/л/30
2/л/б -і/лЯ 2/л/30
ґ-1
0
0^
0
0
0
)
1
о
0
\
-1/'л/2 і/л/2 0
0
0 1
і/л/2
і/л/2 0
\
Гі
0
°1
0
5
0
,0
0
5,
Гла
в а б
6.1.
а)
(2
2^
2
-1
б)
(
1 -1/2
Л
1/2 З
в)
0Ї
-2
г)
0
3/2^
3/2
0 ,
г 1
0
-зі
Ґ4
0
°1
{
3
0 0^ Г
0
1/2
д)
0 -2
0
;е)
0 1 -1
;є)
0
-1 0
;ж)
1/2
0
0
Ь
,°
-1
°,
V
0
0
5
У
1-1
0
-її
з)
ГО
2 0 0Ї
2
10 0
0
0-2-1
0
0-1 З
;І)
3
0 0 -1/2^
0
10 о
0
0-1 о
-1/2
0 0 2
6.2.
а)
1; б)
2
;
в)
3
;
г)
2
;
д)
4 .
6.3.
а)
, х
2
)={х
х
х
2
)
б) ь(х
]
,х
2
)
=
(х
1
х
2
)
в) і(х,,х
2
) =
(х
1
х
2
)|
Г з
-3^
І-з
2,
4*2,
0
3/2
Л
3/2
1 .
*1
1*2
-і о¥*,
4
0
2
І
х
2.
