Тевяшев А.Д., Литвин О.Г., Кривошеєва Г.М. та ін. Вища математика у прикладах та задачах. Ч 2
Подождите немного. Документ загружается.

§3.
Теорія поля
281
2) Обчислюємо циркуляцію С за формулою Стокса:
С = $(а,а?)=
Ц(тоІа,п)скі,
де о - будь-яка поверхня, натягнута на замкнену криву Ь .
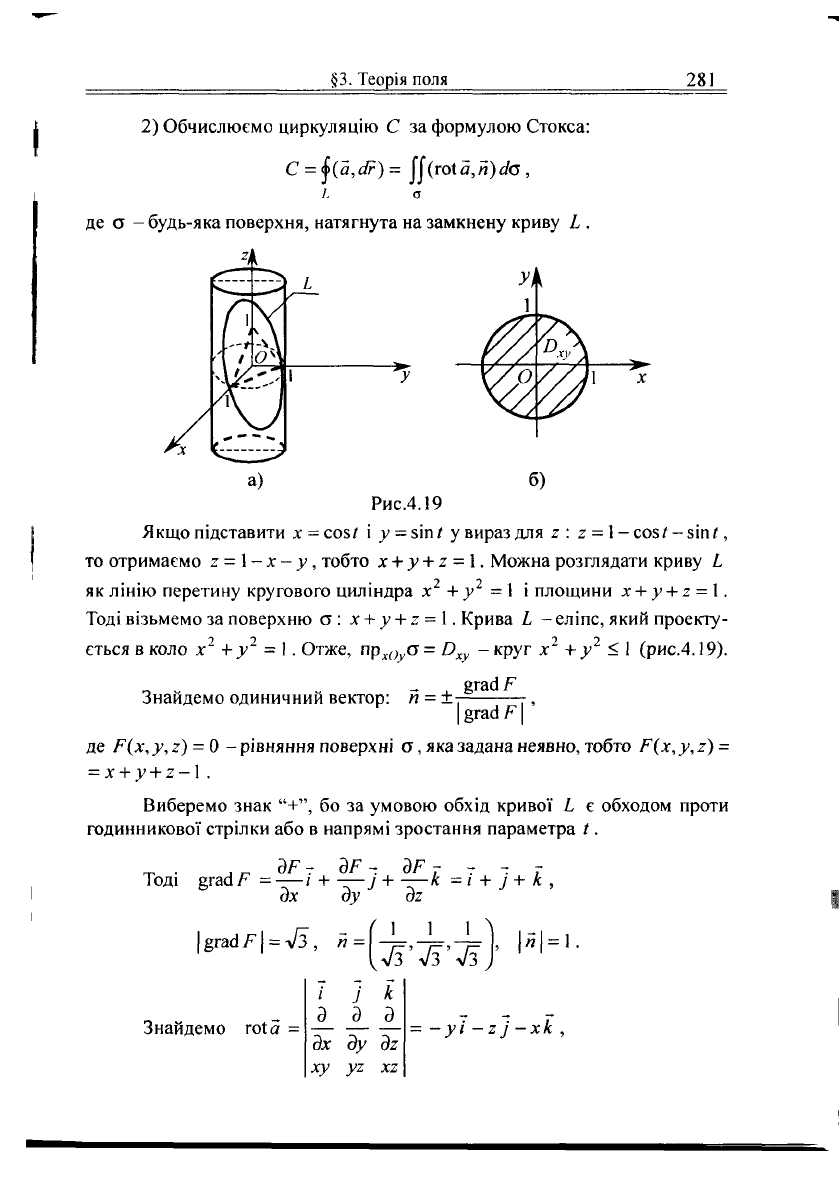
а) б)
Рис.4.19
Якщо підставити х = сові і у = зіп/ у вираз для г: г =
1
- соз/-зіп?,
то отримаємо 2 =
1
- х - у, тобто х + у + 2 = 1. Можна розглядати криву Ь
як лінію перетину кругового циліндра х
2
+ у
1
=
1
і площини х + у + 2 = 1.
Тоді візьмемо за поверхню о : л: +
_у
+ 2 = 1. Крива Ь - еліпс, який проекту-
ється в коло х
1
+у
2
= 1. Отже, пр^а = О
ху
- круг х
2
+ у
2
<
1
(рис.4.19).
егасі
Знайдемо одиничний вектор: п = ±- ,
| бгаа* Р |
де /^(л', _у,г) = 0 - рівняння поверхні а, яка задана неявно, тобто
Р(х,у,г)
=
= X + у +
2
-
\
.
Виберемо знак "+", бо за умовою обхід кривої Ь є обходом проти
годинникової стрілки або в напрямі зростання параметра /.
дР- дР~ дР
Т
~ ~.
Т
Тоді &гайР =— і + — 7 + — к =і + ) + к ,
дх ду дг
Знайдемо гоїа =
/ / к
А А А
дх ду дг
ху уг хг
= -уі -г)-хк ,

282
Глава 4. Криволінійні інтеграли. Поверхневі інтеграли. Теорія поля
тоді (гоіа,й) = —у=(х + у + г), |соз7І =
—
л/3
л/З
Отже,
С = \\(гоі а,п)сіа = \\
(гої а, п)
созу
сіхау = - ^сіхсіу = -8
0
= -п . А
г=\-х-у
Спеціальні види векторних полів
Приклад 12. Довести, що векторне поле
а = (у + г)і + (х + г) і + (х + у)к
потенціальне і знайти його потенціал.
• Необхідною і достатньою умовою потенціальності поля а(М) є
умова гої а = 0 .
Маємо Р(х,у,г) = у + г, (9(х,у,г) = х + г, К(х,у,г) = х + у ,
тоді гої а =
' І к
д_ д_ д_
дх ду дг
у + г х + г х + у
= (1-1)/+(1-1)./+(1-1)*=0.
Виберемо криву інтегрування як вказано на рис.4.20.
,М(х,у,г)
У
Рис.4.20
М(х,у,:) М(х,у,г)
и(х,у,г) = ^Рсіх + <2ау + Кск = ^{у + г)сіх + (х + г)сіу + (х + у)сіг
М
0
<х
0
,Уо,го) 0(0,0,0)
= |(0 + 0)Л+ ^(х + 0)сіу+ І(х + у)сЬ + С= 0 +х]сіу+ (х + у)]
сіг
+ С =
0 0 0 0 0
= ху + (х + у)г + С = ху + хг + уг + С .
Отже, и(х, у,г) = ху + хг + уг + С , де С - довільна стала. М

§3.
Теорія поля
283
Приклад 13. Довести, що векторне поле
а = 2хуг і - у (уг +
1)
у + г к
соленоїдальне.
• Згідно з означенням, векторне поле а соленоїдальне, якщо й\V а = 0.
Знайдемо Ш'УД :
_ дР дО дії „ , ,
п
агуа =— + —+ — =
2у2-2уг-\
+
\
=0 .
Зх Зу Зг
Отже, векторне поле а соленоїдальне. -4
Оператор Гамільтона
Приклад
14.
Використовуючи оператор Гамільтона ("набла"),
знайти вирази для:
1) §гасі(т0,2) сііу(ах6),3) гої(и-а), 4) гоігоіо,
де м = м(х,>>,.г),
V
= \{х,у,г), а = а(х,у,г), Ь = Ь(х,у,г).
і і
• 1) §гаа(т>) =
У(УУ)
=
У'(ИУ)
+
У(ИУ) =УУИ +ИУУ
=
= у§гаам+ м§гаау.
Тут перш за все враховано диференціальні властивості оператора V .
Стрілкою вказано множник, до якого застосовується цей оператор.
2) йі\(ахЬ)=У(ахЬ) =Ч{ахЬ) +Ч(ахЬ) =(У,а,Ь)
+(У,а,Ь)
=
і А
= (Ь,У,а) -(а,У,Ь)= Ь(Уха) -а(ЧхЬ)= Ьгоіа -атоіЬ .
Тут перш за все враховано диференціальні властивості оператора V .
Стрілкою вказано множник, до якого застосовується цей оператор. Потім роз-
глянули кожний доданок як мішаний добуток векторів та скористались влас-
тивістю циклічної перестановки множників у цьому добутку (для мішаного
добутку векторів а, Ь ,с ця властивість така: (а,Ь,с) = (Ь,с,а)= (с,а,Ь) =
= - {Ь, а,с) = - (с, Ь, а) =- (5, с, Ь); тут використане послідовно таке: (а,Ь,с) =
і 4. -І- -І-
(с,а,Ь)= -(£,3,с),тобто
(У,Й,£)
=
(£,У,а),
(У,а,Ь)
=
-(аУ,Ь)).
3) гоІ(иа)= Ух(иа) = Ух(и-й) +Ух(и-а) =
= -ох(Ум) +и(Уха) = -(ах§гас!и) +ихоХа .

284
Глава 4. Криволінійні інтеграли. Поверхневі інтеграли. Теорія поля
Тут перш за все враховано диференціальні властивості оператора V .
Стрілкою вказано множник, до якого застосовується цей оператор. Потім
розглянули кожний доданок як векторний добуток векторів та скористались
в першому доданку властивістю антикомутативності векторного добутку
(ахЬ = —ф ха)), в другому - тим, що скалярний множник виноситься за
знак векторного добутку (а х кЬ = к (а х Ь)).
4) ГОІГОІО= Ух(Ухй) =У(У5) -а(УУ)= §гасі(сііуй) -У
2
а.
Тут використане представлення подвійного векторного добутку через
скалярні добутки векторів (для подвійного векторного добутку векторів а,
Ь , с це представлення має вигляд: ахфхс) = =Ь(а,с)-с(а,Ь)).Л
IV. Задачі для практичних занять
Скалярне поле та його характеристики
4.123.
Знайти і побудувати лінії рівня заданих скалярних
полів:
2
У
а)
и = у + х; б) и = ху ; в) и
= —
.
х
4.124.
Знайти і побудувати поверхні рівня заданих скаляр-
них
полів:
а)
и = х
+
у
+
2 ; б) и = х
2
+ у
2
- 2
і
; в) и = х
2
+ у
2
- 2.
4.125.
Знайти градієнти заданих скалярних полів и = и(г),
г
=хі + у і + гк :
а)
и
= |
г |; б) и =
1п |
г |; в) и =
(5,
г), а - сталий вектор.
4.126.
Обчислити §гад и, якщо
2
1
а)
и = г; б) и = г ; в) І/ =
—;
г)
м
= /(г);
г
де
г = |г | = л/^
2
+ ^"
2
+ г
2
.
4.127.
Знайти величину і напрямок градієнта поля
т
"1 т
и
= х +у +2 -Зхуг в точці А
(2,1,1).
Визначити, в яких точ-
ках
градієнт поля перпендикулярний до осі Ог і в яких точках
дорівнює
нулю.

§3.
Теорія поля
285
4.128. Знайти кут між градієнтами поля и = х
2
+ 2у
2
- г
2
в точках і
>
|(2,3,-1) та
Р
2
{\,-\,2).
4.129. Знайти похідні від заданих полів в заданих точках
за заданим напрямом:
а) и =
х
2
+—
у
2
у точці Р
0
(2,-\) за напрямом вектора
іУЬде ^,(6,2);
1 2 1 2
б) м =
—
х ~
—
У
+2
у точці Р
0
(2,1,1) за напрямом пря-
.. х-2 у
—І
г-\
мої —-— = — = ^ в сторону зростання поля;
2 2 2
ч
Х
У
2
• п / і. ч
в) и = —
ч-
^-г-
+ — у точці Р
0
(а, о, с) за напрямом радіу-
а Ь с
са-вектора цієї точки.
4.130. Знайти швидкість та напрямок найшвидшого зрос-
тання поля и = хуг у точці Р
0
(1,2,2).
4.131.
Знайти одиничний вектор нормалі до поверхні рів-
ня поля и = х +2ху-4уг у точці
Р
0
(\,\,
—
1), напрямлений у
бік зростання поля.
Векторне поле та його характеристики
У задачах 4.132-4.137 знайти векторні лінії заданих век-
торних полів.
4.132. а = у і - х ]'. 4.133. а = хі - у і .
4.134. а = у і + ) . 4.135. а=г=хі +уі
+
гк .
л
- ІГ 1 - ІГ
4.136. а =
—
і
ч— 7
Ч-
—
к .
хуг
4.137. а = (у - г)
ІЧ-
(г - х) ] + (х - у) к .

286
Глава
4. Криволінійні інтеграли. Поверхневі інтеграли. Теорія поля
У задачах 4.138 - 4.141 обчислити дивергенцію і ротор
заданих векторних полів.
4.138. а = г = хі + у і + гк .
4.139. а = (у
2
+ г
2
)І + (г
2
+ х
2
)] + (х
2
+ у
2
)к .
4.140. а =
х
2
уг
і +
ху
2
г у
+
хуг
2
к .
4.141.
а = §гас1(х
2
+ у
2
+ г
2
) .
4.142. Знайти дивергенцію векторного поля
а = х
2
_у / + ху
2
у + г
2
к в точці Р(\, 2, -1).
4.143.
Знайти дивергенцію градієнта скалярного поля
и = х у г в точці Р(1,-1,1).
Обчислення
потоку векторного поля
У задачах 4.144-4.151 знайти потік векторного поля а
через замкнену поверхню а у напрямі зовнішньої нормалі, ви-
користовуючи формулу Остроградського-Гаусса.
4.144. а = х
3
і + у
3
і - г
3
к , а - поверхня куба 0 < х < а ,
0<у<а,
0<г<а.
4.145. а
=•-?-—.,
г=хі+уі
+ гк, о - поверхня сфери
І
^
І
Х
2
+у
2
+2
2
=К
2
.
4.146. а = х
2
у і + ху
2
] + хуг к , а - поверхня тіла
х
2
+у
2
+г
2
<Я
2
,х>0,у>0,г>0.
4.147. а = х
2
у і -
ху
2
і
+ (х
2
+ у
2
)г к , а - поверхня цилінд-
ричного тіла х
2
+ у
2
< Я
2
, 0 < г < Н.
4.148. а = (х - у) і + (х + у) і + г
2
к , а - поверхня цилінд-
ричного тіла, обмеженого поверхнями х
2
+ ^
2
= 1, г = 0, г = 2.

§3.
Теорія поля
287
4.149. а = х
3
/' + у? і + гк , а - поверхня сфери
х
2
+у
2
+г
2
=К
2
.
4.150. а = хі -2у
у
- гк, а - поверхня тіла, обмеженого
параболоїдом
1
- г = х
2
+ у
1
та площиною г = 0.
4.151.
5 = Зх / - у ) - гк , а - поверхня тіла, обмеженого
7 7
параболоїдом 9 - 2 = х +
_у
та площинами х = 0,_у = 0,2 = 0.
4.152. Довести, що потік радіуса-вектора 7 через будь-яку
замкнену поверхню у напрямі зовнішньої нормалі, дорівнює
потрійному об'єму тіла, обмеженого цією поверхнею.
4.153.
Знайти потік радіуса-вектора 7 через повну поверхню
циліндра х
2
+ у
2
< К
2
, 0 < г < Н у напрямі зовнішньої нормалі.
4.154. Знайти потік радіуса-вектора 7 через бічну поверх-
7 7 7
ню циліндра х
+
у < К , 0 < г < Н.
4.155. Обчислити потік радіуса-вектора 7 через бічну по-
верхню кругового конуса, основа якого знаходиться на площині
хОу, а вісь співпадає з віссю Ог . Висота конуса Н = 1, радіус
основи Я = 2.
4.156. Знайти потік векторного поля а = угі + хг] + хук
через бічну поверхню піраміди з вершиною в точці 5(0,0,2),
якщо основою піраміди є трикутник з вершинами {7(0,0,0),
Л(2,0,0) і 5(0,1,0).
У задачах 4.157 - 4.163 обчислити потік векторного поля
а. через задану незамкнену поверхню а у вказаному напрямі.
4.157. а = (х - Зг) / + (х + 2у + г) ] + (4х + у) к , о - верх-
ня частина площини х + у + г = 2, що лежить в першому октанті.
4.158. а = 8х/ +11уу
+\7гк
, а - частина площини
х + 2у + Зг =
1
(нормальний вектор якої складає гострий кут з
віссю Ог), розташованої в першому октанті.

288
Глава 4. Криволінійні інтеграли. Поверхневі інтеграли. Теорія поля
4.159. а = х
2
і +у
2
і-гк, а - частина поверхні конуса
г
2
= х
2
+ у
2
(нормальний вектор якої утворює гострий кут з
ортом к ), що відтинається площинами 2 = 0, 2 = 3.
4.160. а = у
2
г і +хг і + X
і
у к , о - частина поверхні па-
раболоїда 2 = х
2
+ у
2
(нормальний вектор якої утворює тупий
~*
2 2
кут з ортом к ), що вирізається циліндром х + у = 1.
4.161.
а = х
2
і + гк, о - частина поверхні параболоїда
г = х
2
+ у
2
(нормальний вектор якої утворює тупий кут з ортом
к ), що відтинається площиною 2 = 4.
4.162. а = хі + у і +
2
к , а - частина поверхні гіперболіч-
ного параболоїда 2 = — (х
2
- у
2
), що вирізається площинами
К
х = К , 2 = 0, х = 0, орієнтовної у відповідності з напрямком
орта к .
4.163.
а = х
2
/' + у
2
і + гк , а -частинаповерхнігіперболіч-
ного параболоїда г = ~(х
2
- у
2
), що вирізається циліндром
і?
х
2
+ у
2
= К
2
, орієнтовної у відповідності з напрямком орта к .
Лінійний
інтеграл і циркуляція
4.164. Обчислити лінійний інтеграл
^{а,а7),
якщо
ОА
а
=
2І+х]'
+ ук, рівняння дуги ОА: г =1і +1
2
] + (
г
к ,
0</<1.
4.165. Обчислити лінійний інтеграл §(а,аг), якщо
ОА
а
= -уг і +хг і + хук , дуга ОА - перший виток гвинтової лінії
х = дсоз/, у = авт1, г = кі
(0<1<2к).

§3.
Теорія поля
289
У задачах 4.166 - 4.171 обчислити циркуляцію векторного
поля а вздовж замкненої кривої Ь у заданому напрямі обходу
двома способами: 1) безпосередньо, використовуючи означен-
ня циркуляції; 2) за допомогою формули Стокса.
4.166. а = г і + (х + у)) + у к , Ь - контур трикутника,
отриманого від перетину площини 2х + у + 2г = 2 з координат-
ними площинами, при додатному напрямі обходу відносно нор-
мального вектора площини п = (2,1,2) .
4.167. а =
2
і + х ) + ук , Ь
:
х
2
+ у
2
= 4, 2 = 0 при додат-
ному напрямі обходу відносно орта к .
4.168. а = -уі +2і + к , Ь - лінія перетину конуса
х
2
+ у
2
-г
2
=0 з площиною 2 =
1
при додатному напрямі об-
ходу відносно орта к .
4.169. а = у
2
і + ху і + (х
2
+ у
2
) к , Ь - контур, що виріза-
7 7
ється в першому октанті з параболоїда х + у = Кг площина-
ми х = 0, у = 0 , 2 = К в додатному напрямі обходу відносно
зовнішньої нормалі поверхні параболоїда.
4.170. а = 2
2
і +х
2
і + у
2
к , Ь - лінія перетину сфери
х
2
+ у
2
+ г
2
= К
2
з площиною х + у + г = К в додатному напря-
мі обходу відносно орта к .
4.171.
а = 2
і
і + х
3
/ + ук , Ь - лінія перетину гіперболої-
да 2х
2
- у
2
+ г
2
= К
2
з площиною х + у = 0 в додатному напря-
мі обходу відносно орта і .
4.172. Обчислити потік ротора векторного поля
а
= уі
+2і
+ хк через поверхню параболоїда обертання
2
= 2(\-х
2
- у
2
), яка відтинається площиною 2 = 0. Викорис-
тати теорему Стокса.

290
Глава
4.
Криволінійні
інтеграли.
Поверхневі
інтеграли.
Теорія поля
Спеціальні види векторних полів
У задачах 4.173
-
4.177 перевірити, що векторне поле
а(М)
потенціальне
і
знайти його потенціал.
4.173.
а
= (3х
2
у-у
3
)7 +
(х
3
-Зху
2
)].
4.174.
а
=
уг
і +гх
у
+хук
.
4.175.
а
=
(у
+
г)7
+
(х
+
г)]
+
(х
+
у)к .
4.176.
а
= 2ху і +
(х
2
-
2уг)
у
- у
2
к .
4.177.
а
=
(уг -
ху) і
+
(
г
2 \
X
2
хг
К
уг
V
2
,
І + (ху +
у г)к.
У задачах 4.178
-
4.181 перевірити,
чи є
векторне поле
а{М) соленоїдальним.
4.178.
а
=
(х
2
у
+
у
3
)7
+
(х
3
- ху
2
)] .
.27
4.179.
а
=
ху і
+
х у/
+ (х +
у )гк
4.180.
а
!-и-^]-
{х+у)ІП2
к.
уг
хг ху
л!х
2
+у
2
(х
2
+у
2
/
2
Оператор Гамільтона
У задачах 4.182
-
4.183 довести вказані співвідношення,
використовуючи оператор Гамільтона ("набла").
4.182.
дтасі
(«V)
=
V
§гас!
и + и
§гас1
V
;
СІІУ
(иа)
= и йі\ а+а §гад и;
гої (и
•
а)
= и
тої
а +
[§гао!
и, а];
СІІУ
[а, Ь ] = (Ь,
тої
а) - (а,
тої
Ь).
4.183.
гої§гас1г/ = 0; с1іуго1а =
0.
