Тевяшев А.Д., Литвин О.Г., Кривошеєва Г.М. та ін. Вища математика у прикладах та задачах. Ч 2
Подождите немного. Документ загружается.

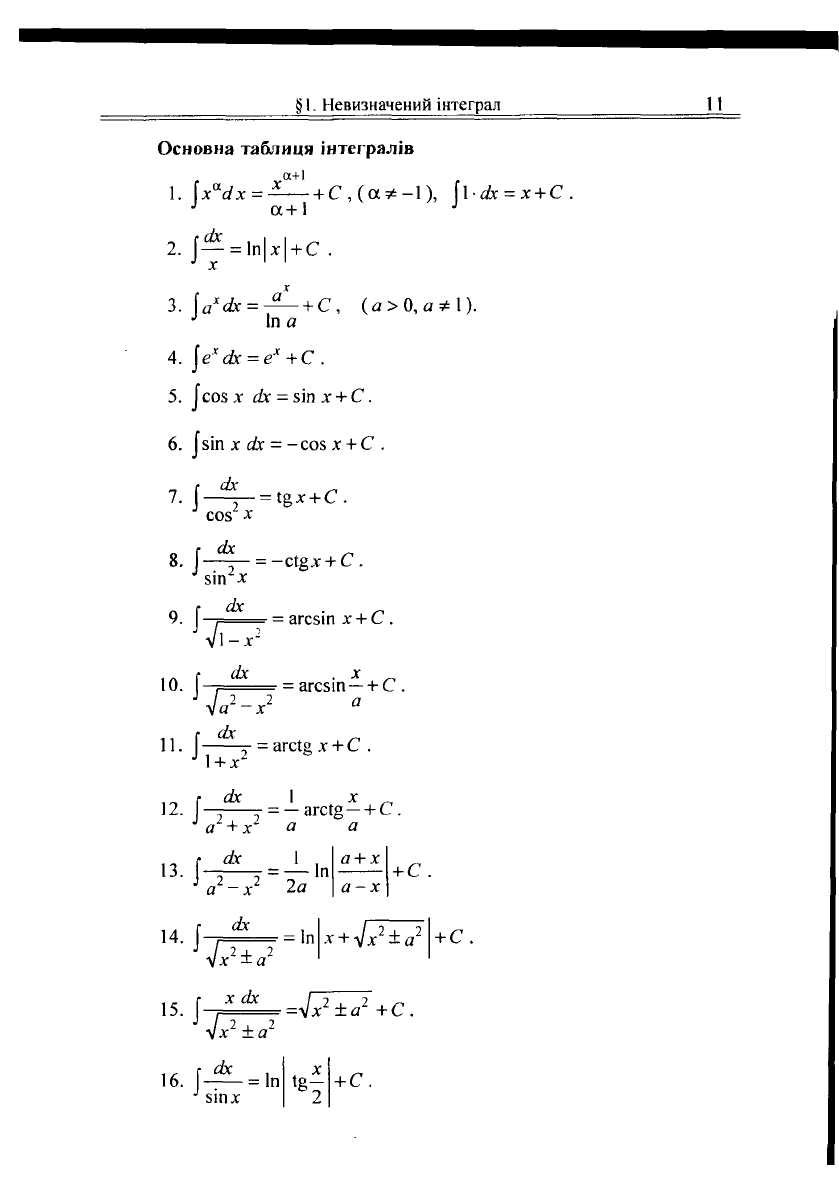
§ І. Невизначений інтеграл
11
Основна таблиця інтегралів
а+1
1
2.
3.
4.
5.
6.
7.
10.
11.
12.
13.
14.
15.
16.
Лі = — + С,(а*-1), [іах = х + С
а+1 -
1
аг
= 1п х +С .
а
х
ах = -^— + С, (а>0,а*\).
1п а
соз х ах-^тх + С.
зіп х ах = -соз х + С .
ах
соз х
ах
= і%х + С.
8ІП
2
Х
ах
-СІ2.Х
+ С .
агсзіп х + С.
ах . х
= агсзіп —+ С.
п—'•
У
а ~х
сіх
\ + х
1
ах
агсі§
х + С .
а
2
+ х
2
а
ах 1
агсіе
—
+ С.
2
-~
2
2а
1п
а -х
ах
а
а + х
а-х
+ С .
1п
х +
+ С .
ах
4х
2
±а
ах
•=47±а
2
+ С.
1п
51ПХ
+ С.

12
Глава 1. Інтегральне числення функцій однієї змінної
18.
|і£ д: ах =
-1п|со5х|
+ С .
19.
|с!§ х ах = 1п|$іпх| + С .
20.
|зп х о5с = сп х + С .
21.
|сЬ х ах = 5гі х + С .
22.
[-^- = іЬх + С.
23.
[-^- = -сйі х + С.
Безпосереднє інтегрування. Обчислення невизначеного інтеграла з
використанням таблиці інтегралів та властивостей інтегралів називають без-
посереднім інтегруванням. Для обчислення невизначеного інтеграла, як пра-
вило,
виконують тотожні перетворення підінтегральної функції, щоб звес-
ти інтеграл до табличного. Крім того, використовують метод підведення під
знак диференціала, який випливає з властивості 6° невизначених інтегралів.
Ця властивість означає, що вигляд формули інтегрування залишається незмін-
ним незалежно від того, чи є змінна інтегрування незалежною змінною, чи
деякою диференційовною функцією (інваріантність формул інтегрування).
Отже,
якщо
Метод підведення під знак диференціала в багатьох випадках дозво-
ляє зводити інтеграли до табличних.
Основні методи інтегрування
Метод заміни змінної (метод підстановки). Якщо функція /(*)
—
неперервна і х = ф(/), де ф(/) та <р'(7) неперервні, то
\Дх)ах = Г(х) + С,
то
(1-2)
(1.3)
Функцію ф(0 підбирають таким чином, щоб права частина у записа-
ній формулі мала вигляд, зручний для інтегрування. Після інтегрування слід
повернутися до старої змінної.

§1.
Невизначений інтеграл
13
Метод інтегрування частинами. Якщо
и - и{х) і
V
= у(х) -
диферен-
ційовні функції,
то має
місце формула
|м
аЧ»
=
ИУ-|у
а'и. (1.4)
Ця формула називається формулою інтегрування частинами. Засто-
совувати
її
доречно, коли інтеграл
у
правій частині формули більш простий
для знаходження,
ніж у
лівій,
або
йому подібний.
Взагалі, інтегрування частинами застосовується
для
інтегрування
де-
яких трансцендентних функцій (наприклад, агсзіп
х ,
агсІ§
х , 1п х ), а
також
добутків алгебраїчних
і
трансцендентних функцій.
Наприклад,
^ Р
п
(х) со$ ах ах ,
^Р
п
{х)
$т ах ах ,
^Р
п
(х)е
ах
ах,
^Р
п
{х)
агсі§ х ах ,
\Р„(х) агсзіп
х ах ,
^Р
п
{х)\пх
ах,
^е
т
со5$хах,
^е"*
зіп р\г ах,
тощо.
Тут
Р„
(х) -
многочлен.
При цьому,
як
правило,
за и
береться така функція,
яка при
диферен-
ціюванні спрощується,
а за а\ -та
частина підінтегрального виразу, інтег-
рал
від
якої відомий
або
може бути знайдений. Наведемо деякі рекомендації
щодо вибору
и .
Якщо підінтегральна функція
має
вигляд:
а)
Р„(х) соз ссе, Р„{х) зіп ах , Р
п
(х) е
ш
, то за и
приймають много-
член
Р
п
(х);
б)
Р„{х) 1пх , Р„(х)
агсзіп
х , Р„(х)
агсІ§
х , то за и
приймають відпо-
відно функції
Іпх ,
агсзіп
х ,
агс!§
х ;
в)
е
0
" созР*, е
0
"
зіп(3х
, то
немає різниці,
що
брати
за и : чи є"*, чи
созР* або
зіпрх.
Зазначимо також,
що
інтегрування частинами може застосовуватись
повторно.
Інтегрування основних класів елементарних функцій
Інтегрування раціональних дробів. Раціональним дробом назива-
Р
(х)
ється дріб вигляду
———, де
Р
т
(х),
<2
п
(х)
-
многочлени степенів
т і п
£„(*)
відповідно.
Раціональний дріб називається правильним, якщо
т < п, у
противно-
му разі, коли
т> п,
дріб називається неправильним.

14
Глава
1,
Інтегральне числення функцій однієї змінної
Найпростішими дробами називаються правильні дроби такого вигляду:
..А
,
ч
А Ах + В
л
. Ах
+
В
1)
; 2)- 3) — ; 4)— --
г
,
х
- а (х-а) х + рх
+
а (х + рх
+
а)
к
2
де
А, В, а,р,ц -
дійсні числа,
&
є ІЧ, к > 1, —— ц < 0,
тобто квадратний
4
тричлен
х
1
+ рх + д має
комплексні корені.
Р
(х)
Кожний правильний дріб
—
може бути розкладеним
на
суму скін-
б„(*)
ченного числа найпростіших дробів вказаних чотирьох типів.
Це
розкла-
дання здійснюється таким чином.
Нехай знаменник
д„(х)
=
Ь„х"+Ь
п
_
]
х"^+...
+ Ь
]
х + Ь
0
має дійсні корені а
ь
а
2
,...,а
к
кратностей х
]
,х
2
,...,х
к
і
комплексно-спря-
жені корені
Р],
р],...,
(З/,
р/
кратностей
А-,,
г,,...,//. Тоді
<^„{х)
(при Ь
п
-\)
представляється
у
вигляді
&,(*)
= (х - а,
)
4
'...
(х -
а
к
У*
(х
2
+
/>,х
+
</,
)
г
1
• • •
(х
2
+ р,х
+
я,)
п
,(1.5)
ДЄ
3]+8
2
+.-.
+ 5
к
+2(Г, +Г
2
+... + Г/) = п ,
х
1
+р
у
х
+ д
у
=(х-Р
ї
Х^-Р
ї
),
У
= 1,/•
~
. Ли(*)
Тоді розклад дробу
—
2
на
суму найпростіших дробів
має
вигляд:
Р«,(х)
=
А,
|
А
2 |
, ,
£„(*) (х-а,)
41
(*-а,)'
Н
""
+
+
в
\
в
2
В
+
!
+ Г + ... + — +
(х-а
к
У" (х-а
к
У*~
]
х-а
к
|
С,х + Р,
|
С
2
х + Р
2 ( ;
^х + Р,, ^
{х
2
+р
х
х +
Чі
У
(х
2
+р
1
х +
д
і
У
і
~
[
"' х
2
+
+
+
|
М,х + ^,
|
М
2
х
+
М
2 |
^ Ау + *г, ^ ^
(х
2
+
/?,х
+
<7,
/' (
х
2
+ ^ +
Ц{
)
г
і
_І
х
2
+ р,х
+
<?,
'
де коефіцієнти
А В,, С
(
, 0,,...,М
п
Л
1
,
повинні бути обчислені.
Для їх
обчислення можуть бути застосовані такі методи:

§1.
Невизначений інтеграл
15
-метод невизначених коефіцієнтів. Суть методу: призводимо рівність
(1.6) до загального знаменника і отримуємо тотожність двох многочленів.
Прирівнюючи коефіцієнти при однакових степенях х, приходимо до систе-
ми лінійних рівнянь відносно шуканих коефіцієнтів;
-
метод задання частинних значень. В отриманій тотожності двох
многочленів надаємо змінній х значення коренів знаменника, що особливо
зручно, якщо ці корені дійсні та різні.
Часто буває корисно комбінувати обидва ці методи.
Процес інтегрування раціонального дробу складається з таких етапів:
а) якщо задано неправильний раціональний дріб, слід виділити з ньо-
го цілу частину, тобто представити його у вигляді
Є„(*)
де М
т
_
п
(х) - многочлен степеня т-п>0, Я
г
(х) - многочлен степеня
г < п, тобто дріб —-—— правильний,
&(*)
б) розкласти знаменник дробу на лінійні і квадратичні множники за
формулою (1.5),
в) правильний раціональний дріб розкласти на найпростіші дроби за
формулою (1.6),
г) обчислити невизначені коефіцієнти А В,, С,, Д,...,Л/,, /V, в
розкладі (1.6), використовуючи метод невизначених коефіцієнтів або метод
задання частинних значень, або комбінуючи ці методи.
Отже, інтегрування раціонального дробу зводиться до знаходження
інтегралів від многочлена та від найпростіших дробів.
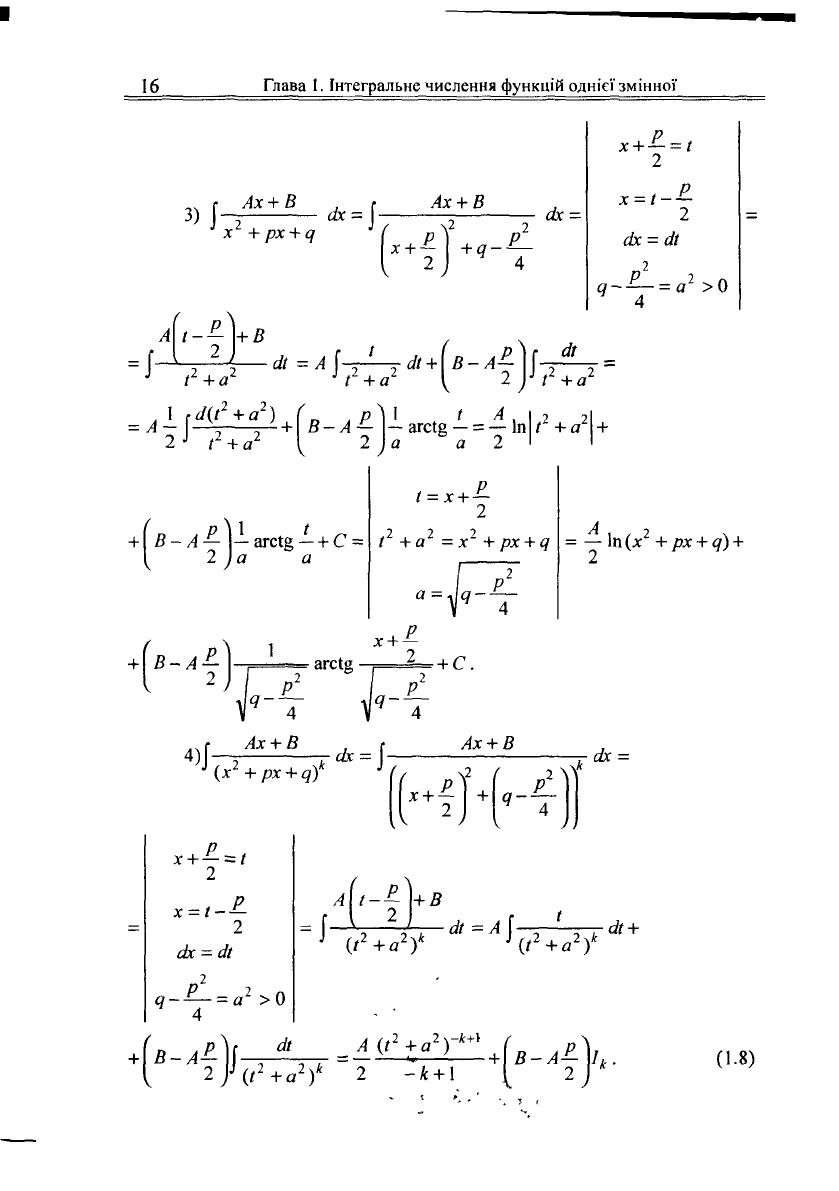
Розглянемо, як знаходяться інтеграли від найпростіших дробів.
А ^ _
л
(О'(х-а)
х-а
2) Г —
г
ах = А
\{х-аУ
к
с!(х-а) = А^^ + С =
\х-а)
к
-
1
-А + 1
Чт+с
1-А (х-а)*-
1
16
Глава 1, Інтегральне числення функцій однієї змінної
„
ч
г Ах + В ,
(
3) \— ах = \
х + рх + д
Ах + В
\2 2
Х+
Р)
+ д
_£_
2)4
ах =
р
Х + —-1
х = І-£-
ах =
аЧ
4
1-Р-\+В
і
2
+а
2
2
і
і
2
+а
2
І 2
І +а
Л
І
' Л , 2 2
агсІ§ — = — 1п г + а +
а а 2
+
(в-А-
Р
-
|-агсІ£- + С =
І 2 ) а а
І = х + -
I
2
+а
2
= х
2
+ рх + д = — \п(х +РЛГ + ^) +
б-Л-
1
х +
-
агсІ§
:
+ С.
і
{х
2
+рх + д)
к }
(
Ах + В
42 / 2 \\
Х+
Р)
+
2 4
х + ^^і
х = ,-Р
ах =
сії
д-^— = а
2
>0
4
}
(і
2
+а
2
)
к 3
(1
2
+а
2
)
к
2У(
(
2
+а
2
)
к
~2 -'* + ! Т ^2 ^
(1.8)

§1.
Невизначений інтеграл
17
Тут позначено /
к
= |—^
(Г+а
2
)
к
'
(1.9)
Для обчислення 4 використовується інтегрування частинами, в ре-
зультаті чого отримується рекурентна формула
1 1
2к
~
3
-І^,к>\.
(1.10)
4 =
2а
2
(А-1)
(/
2
+й
2
)*"'
а
2
2к-2
При А - 1 маємо /, = §
сії
і
2
+ а
2
1 І ^
= —
агсІ§—
+ С.
а а
(1.11)
Формула (1.10) дозволяє після (к -1) - кратного застосування звести
інтеграл до табличного (1.11).
На практиці при невеликих п не використовують формулу (1.10), а
поступово використовуючи інтегрування частинами, приходять до вигляду
інтеграла (1.11). Проілюструємо цей прийом, поклавши в (1.9) к = 2 .
_ л сії 1 га
2
+1
2
-1
2
1 г сії 1 г /
2
(,
2
+а
2
Г а" Г + а
а^(Ґ + а
2
)
2
11 / 1 ,
: — — агсг§ -І.
а' а а а'
Тут
(I
і
+ а
2
)
2
сії-
и = і;
сій
— сії
1 гсі((
2
+а
2
)
(Ґ+а
2
)
2
сії;
2
Л
2
2
і
(I
і
+ а
1
)
(1.12)
2 I
і
+а
2
1 1
+ - — - =—5 Г~
+
агсІ§—+ С.
•
)
'
2
--
2
2(ґ
2
+а
2
)
2 а а
2 і
1
+а 2
і
г +а
Після підстановки в (1.12) отримуємо
І
1
' 1
1
2
= — агс{§ г
а а а
1
1 ? 1
—г-агсІ§ - +-у —5 т-
2а
3
а а
2
2(і
2
+а
2
)
Інтегрування деяких ірра/ііеі.
пис Р.(х
и
х
2
,...,х„) означає раці^
новка, що призводить до
раціоналізуючою.
ВІВЛІОТЕК-
нкцій. Умовимося, що за-
ід п аргументів. Підста-
ві функції, називається

18
Глава 1. Інтегральне числення функцій однієї змінної
Розглянемо деякі типи інтегралів від ірраціональних функцій.
1) 1=\К я,**
1
,х'
2
,...,х'" сіх .
Тут дроби; позначимо к - загальний знаменник цих дробів.
Раціоналізуюча підстановка:
х-Г
.
(1.13)
2) І=\Я
ах+ 6 У, ( ах + Ь^
сх + сі
сх + сі
ах + Ь\,
сх + сі
сіх .
Тут — - дроби; позначимо к - загальний знаменник цих дробів,
а, Ь,с,сі - задані числа, с і сі одночасно не обертаються в нуль.
Раціоналізуюча підстановка:
сос
+ Ь і,
• =
г.
(1.14)
сх + а
Зауважимо, що тип 1) є частинним випадком типу 2) при а = \, Ь = 0,
с = 0, сі = 1.
3)
І=\к^х,4ах
2
+Ьх +
с ^ах, а*0.
Існує декілька підходів до обчислення такого типу інтегралів:
а) виділяємо повний квадрат у квадратному тричлені ах
2
+Ьх + с :
ах +Ьх + с = а
і Ь с
X
+—Х+—
= а
2 „ Ь с
х
+2—х+—
2а
а
( ь
х +
V
2а
2
'£__*! ^
а 4а
2
Далі заміна змінної
х + — = и (1-15)
2а
зводить вихідний інтеграл до одного з таких інтегралів:
\к{и,>І1
2
-и
2
^сіи,
\к\и,^1
2
+и
2
^сіи,
\К^и,лІи
2
-І
2
^сіи,
які знаходяться за допомогою підстановок:

§1.
Невизначений інтеграл
19
и-івті, и = ІХ%1, и = -
С05 І
відповідно;
б) застосовуємо три підстановки Ейлера:
- якщо квадратний тричлен ах
2
+Ьх + с має комплексні корені
(а > 0), то має місце перша підстановка Ейлера
УІах
2
+Ьх + с =1± хт[а ; (1-16)
- якщо с> 0, то застосовується друга підстановка Ейлера
4ах
2
+Ьх + с =х (±л[с ; (1.17)
-якщо ах
2
+Ьх + с = а (х-х
г
)
(х-х
2
),
де х, та х
2
- дійсні корені
тричлена, то застосовується третя підстановка Ейлера
ліах
2
+Ьх + с =1(х-х
}
). (1.18)
4) Інтеграли від диференціальних біномів
І = |дг
т
(а +
Ьх")
р
ах,
де т, п, р- раціональні числа, виражаються
в елементарних функціях лише у трьох випадках. Наведемо ці випадки та
відповідні підстановки:
а) р - ціле число. Підстановка
1 = Ух~, (1.19)
де і - загальний знаменник дробів тій, перетворює вихідний інтеграл
в інтеграл від раціональної функції;
о) ціле число. У цьому випадку раціоналізуюча підстановка
п
а +
Ьх"=1
Л
,
(1.20)
де 5 - знаменник дробу р;
ч
т + \ „ . . . .
в) - + р - ціле число. Раціоналізація інтеграла здійснюється за
п
допомогою підстановки
ах~"+Ь = Г, (1.21)
де 5 - знаменник дробу р.
Інтегрування тригонометричних функцій
1.
Інтеграл вигляду / = |Л($іп х, соз х) сіх раціоналізується за допо-
могою універсальної тригонометричної підстановки

20
Глава 1. Інтегральне числення функцій однієї змінної
Дійсно,
х = 2 агс{§ І
2 сії
21 \~1
2
\2сИ
21
51П
X =
1
+ /
\+1
2
'] + 1
2
)і + 1
2
'
соз де --
\+1
2
2.
Обчислення інтеграла / = |/?(зіп х, соз х) сіх можна спростити у
таких випадках:
а) підінтегральна функція змінює знак при зміні знака зіп х, тобто
б) якщо /?(зіп х,-соз х) = -Л(зіп х, соз х), то раціоналізуюча підста-
новка
в) якщо /?(-зіп х,-соз х) = /?(зіп х, соз х), то раціоналізуюча підста-
новка
і = Щх.
3.
Раціоналізація інтегралів |Л(зіп х) соз х сіх , | Д(соз х) зіпх сіх,
х) сіх здійснюється так:
/?(—зіп х, соз х) = -Л(зіп х, соз х).
Раціоналізуюча підстановка
соз х,
/ = зіп х ,
І = \Н(Щх)сіс
і%х = 1
х = агсІ§ /
