Тевяшев А.Д., Литвин О.Г., Кривошеєва Г.М. та ін. Вища математика у прикладах та задачах. Ч 2
Подождите немного. Документ загружается.


§1.
Невизначений інтеграл
31
б)/=|
Зх-1
<&
= /-
Зх-1
•Ух
2
-4х + 8
ЛІ(х-2)
2
+4
сіх
••
х
—
2 =
1
х =
1
+ 2
сіх =
сії
•
= Зл//
2
+4+5 1п і +
4і
2
+4
+ 4
+ С =
|/
= х-2| = 3-\/х
2
-4х + 8+51п Х-2 + -Л
2
-4х + 8
Приклад
8. Обчислити інтеграл /
1—
х
3
+х
+
2
-сіх.
3)(х-4)
•
Підінтегральна функція є неправильним раціональним дробом. Ви-
ділимо його цілу частину. Для цього, розкривши дужки у знаменнику, діли-
мо чисельник на знаменник:
х
3
+х + 2 х
3
+х + 2
(х-3)(х-4) х -7х + 12
х-
+х + 2
•їх- +\2х
х
1
-7х + 12
х + 1
1х~ -11х + 2
7х
2
-49х + 84
38х-82
38х-82 „ х
3
+х + 2
Таким чином, —г = х + 7
н
х
2
-7х + 12 (х-3)(х-4)
Оскільки квадратний тричлен х - 7х +12 має два дійсних корені, роз-
38х-82 „ . .
клад дробу — — на найпростіші дроби першого типу має вигляд:
(х-3)(х-4)
38х-82
А В
- + -
(х-3)(х-4) х-3 х-4
Зведемо дроби в обох частинах рівності до загального знаменника.
Маємо рівність
38х-82 = Л(х-4) + В(х-3).
Знайдемо коефіцієнти А і В . Застосуємо метод задання частинних
значень,
поклавши послідовно в отриманій тотожності х = 3; х = 4 .
При х = 3 маємо 38-3-82 = -/!; А = -32.

32
Глава
1.
Інтегральне числення функцій однієї змінної
Прих=4 маємо 38-4-82
= 5; 5 = 70.
Отже,
г
X
і
+ х
+
2 , г. _. , Г —32 , Г 70 ,
/
= ах = \{х +
1)ах+\
ах+\ сіх =
•Чх-3)(х-4)
-
1 З
х-3
}
х-4
х
1
=
—+
7х-32
1п|х-3|
+
701п|х-4|
+ С.-*
Приклад
9.
Знайти інтеграл
/ = [
т-сіх.
(х-1)(д:
+ 1)
2
• Підінтефальна функція
є
правильним раціональним дробом, зна-
менник якого
має
дійсні корені, серед яких
є
кратні, отже розклад
на
най-
простіші дроби включатиме найпростіші дроби першого
та
другого типів:
х
А В й
-
+
-
(х-1)(х + 1)
2
(х + 1)
2
(* + 1)
х
= А(х + ])
2
+
5(х-1)+0(х
2
-1).
Використаємо метод задання частинних значень:
при
х =
1
маємо
4А = 1, А=^;
при
х = -1
маємо
-1 = -26, В = .
Далі використаємо метод невизначених коефіцієнтів
для
знаходжен-
ня коефіцієнта
О . Для
цього прирівняємо
у
тотожності коефіцієнти, наприк-
лад,
при х
2
.
Отримаємо:
х
2
|
0 = А + Б, £ = --.
І
4
Остаточно
С
х
сіх
_1ГЙХ 1г ах 1
<•
ах _
*
(х-1)(х + 1)
2
~ 4-І х-1 2^(х + 1)
2
V х + \~
'
х-1
= -1п|х-1І--
— -1п|х + 1І+С = -1п
4
і 1
2 х +
1
4
1 1
4
х
+
1
2(х
+
1)
•
+
С.<
Приклад
10.
Знайти інтеграл
/ = [
--сіх.
і
(х-1)(х
2
+1)
• Підінтегральна функція
є
правильним раціональним дробом, зна-
менник якого
має
дійсний
та
пару камлексно-спряжених коренів. Тому
в
розкладі дробу
на
найпростіші будуть міститись найпростіші дроби першо-
го
та
третього типів.

§1.
Невизначений інтеграл
33
^ . х А Вх + С
Тоді — — = - + —5 •
(х-1)(х
2
+1) х-\ X
і
+1
Звідси А(х
2
+ 1) + (£х + С)(х-1) = х.
При х = 1 отримаємо 1 = 2А,
А=
^- Д
1
"' використаємо метод не-
визначених коефіцієнтів. Складемо систему рівнянь для знаходження коефі-
цієнтів В і С:
2
Л + В = 0
С-В = 1, звідси В = --, С = -.
2 2
Отже,
х 1
— +
—
2 2
1 -х
+ 1
- + -
(х-1)(х
2
+1) х-1 х
2
+1 2(х-1) 2(х
2
+1)
Остаточно маємо
, г х ах \ г ах 1 <•
1
-х . І,. ,і
/= г = -
+
- — ах = -1п х-1 +
•'(х-1Хх
2
+ 1) 2^-1 2-'х
2
+1 2
1 1
1 1 г <І(Х~ +1) 1,1 , І 1 1 , , 2 ,Ч ^, ^
+
—
агсіе х — —Цг - — 1п х-1 +— агсіе х — 1п(х +1) + С. <
2
&
4
і
х
2
+і 2
і 1
2
5
4
Приклад 11. Обчислити І
—
\
сіх
(х
2
+4)
2
Маємо
• Підінтегральна функція є найпростішим дробом четвертого типу.
сіх _ 1 г 4
(х
2
+4)
2
~ 4-І (х
2
+4)
2
&
=
-[
1
г
х
2
+4-х
2
4-
1
(х
2
+4)
2
ЙХ :
X ах
х
/
+4 •'(х
2
+4)
2
_1_
_1_
4 2
х 1 г х ах
агсІ§ —г—
2 4
-
1
(х
2
+
(х'+4)'
Останній інтеграл знайдемо, використовуючи формулу (1.4) інтегру-
вання частинами.
2
X
сіх
/, = [——- ах = їх .
3
{х
2
+4)
2
}
(х
2
+4)
2

34
Глава 1. Інтегральне числення функцій однієї змінної
и = х;
сій = сіх
А:
х сіх
(х
2
+4)
2
1 [
а
(
х +А)
- 1
2*
(х
2
+4)
2
~ 2(х
2
+4)
сіх -х І х
. -т = + -агсІ§ — + С
2 , лч О •! „2 ,4
л/
-„2 ^ 4 2
2(х
2
+4) 2'
х
г
+А 2(х
2
+4)
Отже,
/ =
—
агсіе
8
ь
2 4
X 1 , х
г +—агсіе—
2(х
2
+4) 4 2
+ С =
+ —агсї§ - + С А
8(х
2
+4) 16 2
Приклад 12. Знайти інтеграл / = |
ох
(*
2
+9)
3
"
• Підінтегральна функція є найпростішим дробом четвертого типу.
Знаменник дробу має три пари комплексно-спряжених коренів, к = 3 . Для
обчислення цього інтеграла зручніше скористатись рекурентною форму-
лою (1.10) для обчислення інтеграла вигляду І
к
= ^- ^
(1
2
+ а
2
)
к
1
+ -
1 2*-З
к-\
2а
2
{к-\) (Г
2
+ а
2
)*-' а
1
2к-2
У нашому випадку: показник степеня к = 3; а
2
= 9; / = х . Тому
сіх х 11 2-3-3
(х
2
+9)
3
2-9(3-1) (х
2
+9)
34
+ —•
9 2-3-2
/з-і
=
4 =
^ 1 _1
Зб'(х
2
+9)
2 +
12
У свою чергу
X
—1
2
, ДЄ 1
2
= \
сіх
(х
2
+9)
2
'
її, , г сіх і . д _
+ /,, де /, = — = -агсіе—+ С
2-9 х"+9 9 2
х
2
+9 З
х
З
„ X 1 1 1 X _
Отже, /, = ; + агсіе— + С .
2
18 х
2
+9 18 З З
Остаточно маємо
сіх х 1
'-Ь
(х
2
+9)
3
36 (х
2
+9)
2
12
1 1 х) ^
. + —агсіе— \+С =
„2 ,
п
чл
6
з
(18 х
2
+9 54

§1.
Невизначений інтеграл
35
: + - + агсІ§
—
+ С.
216(х
2
+9) 36(х
2
+9)
2
648 З
Приклад
13.
Знайти інтеграл
/ = |
5х
2
-12
(х
2
-6х + 13)
2
сіх
• Підінтегральна функція - правильний раціональний дріб. Знамен-
ник дробу має дві пари комплексно-спряжених коренів, к—2. Отже розкла-
дання підінтегрального дробу на найпростіші з невизначеними коефіцієнта-
ми має вигляд
5*
-12
Ах + В Сх + Б
(х
2
-6х + 13)
2
(х
2
-6х + 13)
2
х
2
-6х + 13^
Ах+В + (Сх + 0)(х
2
-6х + 13) = 5х
2
-12.
Для знаходження коефіцієнтів А, В, С, О утворимо систему
.3
X
X
X
Тоді
о
С=0
£-6С = 5
Л-6О + 13С = 0
В+130 = -12, звідси Л = 30, В = -77, С = 0, й = 5.
'=1
5х -12
(х
1
-6х + 13)
Т
ах =
1
ЗОх-77 , г 5 сіх
—
Т
сіх+\—
(х
2
-6х + 13)
2
Ч-бх + ІЗ
=
/,+5/
2
.
Розглянемо окремо два останніх інтеграли. Інтеграл /
2
знайдемо, ви-
діливши у знаменнику повний квадрат:
СІХ
сіх сі(х-З) 1 х-3 ^
4
' =-агсі§— + С .
х^-6х + 13 '{х-3)
1
+4
:
{х-3)
2
+4 2 "2
х-3 = /
х = / + 3
7 (
ЗОх-77
г
ЗОх-77
1\
= —, Т сіх =
\х
2
-6х + \3)
2 3
((х-3)
2
+4)
2
сіх =
сіх - сії
30(/
+ 3)-77
(/
2
+4)
2
І-30/ + 13 , „
лГ
Г , ,,г
йх
сії
=
\
—
-ої= 30[
— -А
+
131-у—
}
(і
2
+4)
2
3
и
2
+4)
2
•
З
а
2
+
А
(ҐЧ4)
2
: 30/, +13/, .
сії-
(ґ +4)
1
\гсі(і
2
+4)
=
1 1
|С
2
і
(і
2
+4)
2
2/
2
+4

36
Глава 1. Інтегральне числення функцій однієї змінної
Для обчислення інтеграла /
4
скористаємось результатом, отриманим
у прикладі 11:
Л
ІА
Ч
2
+4)
2
8(/
2
+4) 16
Отже,
І 1 І _
+ — агс!§
—
+ С.
/,
= 30/
3
+13/
4
= ЗО [ - Л і
2
1
-
+ 13
= / =
*-3|
= -
15 13 х-3
13 х-3
= —агсІ§ + ,
16 2 8(х
2
-6х + 13)
Х
2
-6х
+ 13 8 д;
2
-6х + 13 16
13х-159
(
і 1 Л
--+ — агсіе
—
8(/
2
+4) 16 2
13 х-3 ^
агсІ§ + С =
+ С--
+ С.
Остаточно, шуканий інтеграл має вигляд:
/
=
/,+5/
2
13 х-3
—
агсіе ——- + -—
16 2 8(х
2
-6х + 13) 2
13х-159 5 х-3 „
+
—
агсіе. + С :
53 х-3 13х-159
—
агсіе. + т
16 2 8(х
2
-6х + 13)
+ С.<
Приклад 14. Обчислити інтеграл
(х + 1)(х
2
+1)
2
•
Підінтегральна функція - правильний раціональний дріб, знамен-
ник якого має один дійсний і комплексно-спряжену двократну пару коренів.
Тому у розкладі дробу на найпростіші будуть міститись дроби першого, тре-
тього та четвертого типів.
^
. 2х + 3 А Вх + С йх + Е
Тоді — =—-г = - + —= т + —5 >
(х + 1)(х
2
+ 1)
2
х +
1
(х
2
+1)
2
х
2
+1
Л(х
2
+1)
2
+(Вх + С)(х +
1)
+ (Ох + £)(х
2
+1)(х +
1)
= 2х + 3.
При х = -1 маємо 4А = \, Л = -^.
Для знаходження коефіцієнтів В, С, Д Е утворимо систему
Л +
£>
= 0
£ +
£>
= 0
2А+ В + й + Е = 0
В + С + 0 + Е = 2, звідси В = --, С =-,£> = —, £=-.
2 2 4 4

§1.
Невизначений інтеграл
37
Тоді
1 х 5 х І
2х+
2
3
2
*
=
г^-*
+
й^*
+
йІ1І
(х + \)(х
2
+\)
2 }
х + \
1
(х
2
+\)
2 3
х
2
+ 1
ах =
ІПІ Х + 11 -—
[—^—^-ТГ
СІК-——— СІХ
1 1
2
і
{х
2
+\)
2
4
і
х
2
+\
1 г х-1
1 , , І 1г 2х сіх 5 г сіх
•- ІП Х +
1
-- - - +-\ : Г
4
1 1
4
і
(
х
2
+\)
2
2
}
(х
2
+ 1)
2
\ г2х сіх 1 г сіх
8-' х
2
+1
+
4-' х
2
+1
= ііп|х
+
і|-і|
4-!
(х
2
+1)
2 +
2^(х
2
+1)
2
8-" х
2
+ 1
1
г
аЧУ
+ 1) 1
1
+
—
агсІ§ х
-І
•її
1п|х +
11
+ -
1 1
1п(х + 1) + агсі§ х
х
1
-
+1 2
Обчислимо останній інтеграл
сіх
е
х
2
+ \-х
2
, (СІХ
5 г сіх
2
3
{х
2
+\)
2
X сіх
, г ах гх -і-і
—
х , г ах ; х ах
/, = — - - —г сіх = —: х— -т- = атсЩ х -1
2
,
1
(х
2
+\)
1
^
(х
2
+ \)
2 і
х
2
+\
1
(х
2
+ 1)
2
де
І
2
=\,
X сіх
(х
2
+1)
2
и = х;
, х ах і ґ
Л
=
— -; ч =
йи
—
сіх
1
г
</(х
2
+1) 1
(х
2
+1)
2
2
:
(х
г
+іу 2(хЧ1)
сіх
2(х
2
+1) 2
і
х
2
+\ 2(х
2
+1) 2
Тоді
+
—
агсІ§ х + С.
1 х
/, = агсіе х —агсіе х
н
г——
' 2 2(х
2
+1)
Остаточно шуканий інтеграл
+ С = ^-|агсІ§х + ^-
21 х+1
+ С,
І =-
4
1п х +
1
+
1
х
2
+1 2
— 1п(х +1) + агсі§ х
+ —
4
агсІ§ х + —
х'+1
— агсіе х + — ІПІХ + 1І-— 1п(х
2
+1)+
+1
+ С .
2
5
4
1 1
8 4(х
2
+1)
Приклад
15. Відповідною підстановкою раціоналізувати
е СІХ
шдштегральну
функцію та обчислити інтеграл І —\
—=
РГ.
38
Глава
1.
Інтегральне числення функцій однієї змінної
-о/
1
+ /
ах
X =
і
ь
ах
-
=
б?
5
сії
і
= */*"
/
+
1
1
^
г
б/
5
ДЇ ,
Г
Г ,
сії
= 6
ґ
{
3
{
2
___
+
г
_1п|
н
.,|
+с
=
=
І
/ = ^х
І
=
2
л/х
-
3
Ух + 6 Тх - 6
1п (Тх +1)
+ С .
<4
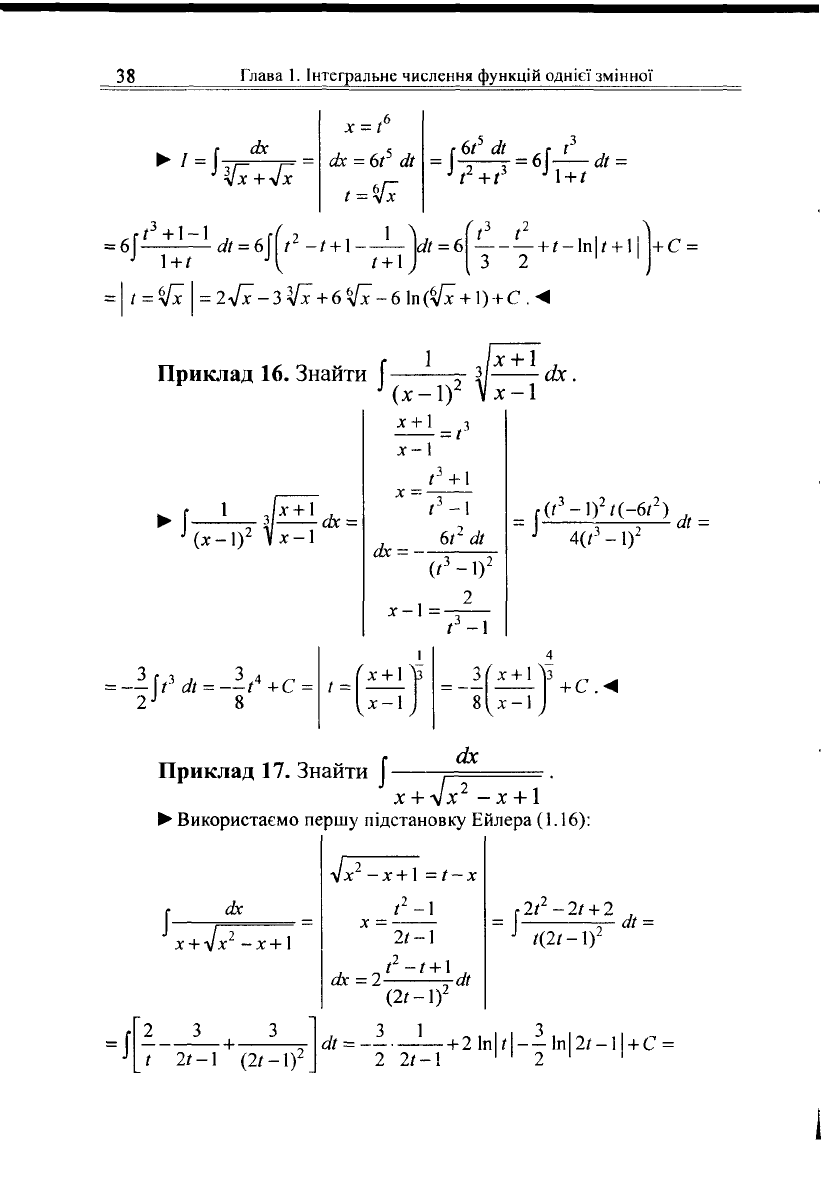
Приклад
16.
Знайти
Г—--—Г-
+
*
ох.
•'
(х-і)
2
и-і
Х
+
1
!
•
= Г
•1
Х+1
(х-1)
2
.х-1
йх
=
х-1
сіх = •
ІІ±1
;
3
-1
б?
2
дї
'(/
3
-1)
2
х-1
=
?
3
-1
Г^І^)^
-
1
4(Г
3
-1)
2
(
х+]
)
3
3
(х
+
\Л
(х-1)
8 {х-\)
+с
.•
сіх
Приклад
17.
Знайти
|— . .
х
+ л/х
2
-х +
1
• Використаємо першу підстановку Ейлера (1.16):
дх
х +
л/7
-х+1
х+1=
г-х
х
=
-
<
2
-1
2/-1
ох
=2
Ґ-1
+
1
(21
-І)
2
дї
г
2Г-2/
+ 2 ,
-
1
/(2/
-І)
2
2
3 З
+ -
/
2?-1
(2/-1)
2
3
1 З
ої
= + 2
ІпШ—1пІ2г-1І
+ С =
2
2/-1
1 1
2
1 1
§1.
Невизначений інтеграл
39
<=4х
2
~-
х+ \ +х
2
2х + 2\/х
2
+
1
-1
2
2х +
2у[х
2
-х +
1
-1 + 2 1п
х +
л/х
2
-х +
1
+ С .<
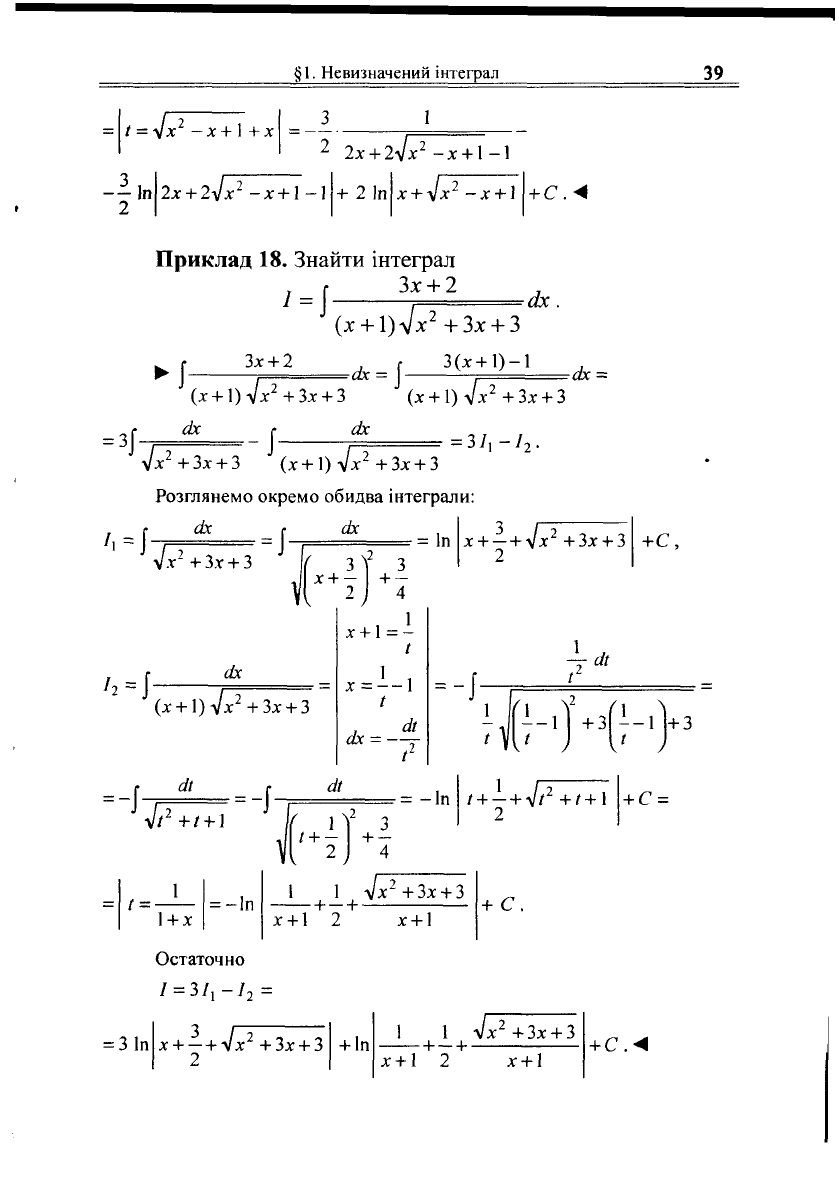
Приклад
18.
Знайти інтеграл
І _ | Зх + 2
•І
(х + 1)л/х
2
+3х + 3
Зх + 2 ,
г
3(х+1)-1
ЙХ .
(х + 1)л/х
2
+3х + 3 (х + 1) >/х
2
+3х + 3
ах г ях
ах =
л/х
2
+3х
+ 3 \х +
1)л/
х^ +3х + 3
Розглянемо окремо обидва інтеграли:
сіх
1п
х- + Зх + З
сіх
х +
-
Х + — +
УІХ
2
+3х + 3
2
+ С,
х^ +3х + 3
х +
1
= -
/
хЛ-1
/
ах = -^г
г
сії
7
ГЧ-І7-
+ 3
/тг
1
—/"
сії
•= -1п
' 1^
2
З
+
—
4
/+—+V/
2
+?+1
+ с
:
1
+ х
= -1п
1 1
л/х
2
+3х + 3
- + —+ •
х +
1
2
х +
1
+ С.
Остаточно
/ =
3/,-/
2
= 3 1п
х + -
+л/х
2
+3х
+ 3
2
+
1п
1 1
л/х
2
+3х + 3
- + —+
х+1 2 х +
1
+ С.<*

40
Глава 1. Інтегральне числення функцій однієї'змінної
Приклад 19. Проінтегрувати диференціальний біном
\( і \
:
3
+1
ах.
• Тут маємо, враховуючи вираз для диференціального бінома
х
т
(а
+ Ьх")
р
сіх ,що т = -\^,п=~^,р = -2, р - ціле число, тому викорис-
таємо підстановку (1.19): х = Ґ ,де 5 - загальний знаменник дробів т =—-
і п =
—
, тобто 5 = 6.
З
Отже,
і ( і Л
X
і
+1 сіх =
, ( і +
1
-
1
,
ґ
( Ж
г(
:6|—
-Ж = 6\- 6|
(І
2
+1)
2
•' '
2
' ' >
х = і
сіх
=
6і
5
сії
сії
и
ь
ж
І\І
2
+1)
2
6/
/
2
оі
(/
2
+ 1)
2
У +1 •'(/
2
+1)
2
багсіе ?-б|
(
Г
2
+1)
2
'
Обчислимо останній інтеграл:
г сії е(
2
+ \-1
2
(1
2
+ \)
2
(/
2
+1)
2
І сії
(Г+1)
(/
2
+1)
2
-
1
(г
2
+і)
2
и =
сій = Ж
1 , ^(/
2
+ 1) 11
(*
2
+1)
2
2
}
(У + іу 2 і
1
+1
' 1 г
= агсІ§
1
+ —-
2(г
2
+1) 2
і
і
2
+1
Ж І 1
= агсіе г + -— агсІ§ і + С
•
2(і
2
+1) 2
1
1
= -агсІ§ /+— -+ С
2 2(/
2
+1)
Остаточно маємо
1=6 агсіе 1-6
і 1
4
- +—агсіе '
^2(/
2
+1) 2
+ С = 3 агсІ§
?
-
Зг
,
2
+1
+ С =
1 = $/х = Загсіел/х -
Зл
^- + С.^
