Тевяшев А.Д., Литвин О.Г., Кривошеєва Г.М. та ін. Вища математика у прикладах та задачах. Ч 2
Подождите немного. Документ загружается.


§1.
Невизначений інтеграл
41
Приклад
20.
Знайти інтеграл
/ = | х
1
+ х
4
сіх
1
+
1
. 1 1 1 т +
1
2
т+1
• Маємо: т = —, п = —, р = —; —^— = 2 , ціле
2 4 3 л }_ п
4
число,
отже, використаємо підстановку (1.20): а + Ьх" = /', де х - знамен-
ник дробу р, тобто х = 3 , а підстановка має вигляд
І
1+х
4
= /
3
.
Таким чином,
І = \х \ + х
4
сік
=
= 12|(/
6
-/
3
)Л=у/
7
-3/
4
+С, де?
Приклад
21.
Обчислити інтеграл
/ = | ^
+ 1=\ *
=1х-\і
+
х*)
1
+ х
4
= /
3
х=(/
3
-1)
4
Л^ігг
2
^
3
-!)
3
^/
/
М2
',
2(
'
3
:
1)3
*=
1
( )_\
1
+ х
4
1
+ х<
2
сіх.
1 +
1
3 1 „ /я +
1
Тут т = —7, и = 4, р = — ; +Р~ =
-
2, + р -
2 п 2 2 п
ціле число, отже, використаємо підстановку (1.21): ах~" +Ь=і\ де х = 2 -
знаменник дробу р. Тоді
/ = {х~
7
(' + *
4
)
2
Л =
1
+ х"
4
=і
2
х = ((
2
-\)
4
<&
= --(> -1)
4
А
2

42
Глава
1.
Інтегральне числення функцій однієї змінної'
-
-( і ^ --
4/(/
2
-1)
2
1
+
Г
-Ц-
>/і
+ х
4
г
=
л/1+х
4
=
ісіі= --[{і
1
-Х)<к = --I
і
+
-1
+
С =
2
і
6 2
д/О
+
х
4
)
3
+~Л/і
+ Х
4
+С.
6х° 2х
Приклад 22. Знайти
/ = [
•' 4 зіп х + 3 соз х
+
5
• Застосуємо універсальну підстановку:
.
х
сіх
4
ЗІП
х +
Зсоз
х
+
5
х
= 2
агсІ§
і
сіх = -
\+Ґ
-сії
зіпх ••
СОЗХ
= -
21
сії сії
2Г+8>
+ 8 '(1 + 2У
1
+ 2
1
+
Ґ
\
+ 1
2
-+с =
і
+
г
2/
+
3
-сії--
\ +
і
2
\ +
і
2
+ 5
х
Приклад 23. Знайти інтеграли:
а)|зіп
3
хйх;
6)|СОЗ
5
ХЙХ.
• Степені лідінтегральних функцій непарні, тому, якщо відокремити пер-
ший степінь зіп
х
(або созх), підвести його під знак диференціала, отримаємо:
а) |зіп
3
х
сіх
=
|(1
-
соз
2
х)зіпх сіх
=
-[(1
-
соз
2
х)
сі (со&х)
=
соз"
х „
:~созх
+ уС ;
б) |соз
5
х сіх
=
|(1
-
зіп
2
х)
2
соз
х
сіх
=
|(1 -2зіп
2
х +
зіп
4
х)
оХзіп
х) =
2
.
3
зіп
5
х
: зіп х—зіп
хн нС
3
5

§1.
Невизначений інтеграл
43
Приклад
24.
Знайти
інтеграли:
а)|соз
2
х
сіх
;
б)|§іп
4
х сіх.
•
Степені підінтегральних функцій парні, тому застосуємо формули
пониження степеня тригонометричних функцій:
а) Гсоз
2
х сіх = — [(1 + соз2х) сіх =
—
х +
—
ш2х + С ;
2
і
2 4
б) |зіп
4
х ах - -соз2х)
2
сіх = -2соз2х + соз
2
2х) ах =
х зіп2х 1г 2~ , х зіп2х 1
Г/
, . . ,
= +
—
соз 2х сіх = + - (1 + соз4х) ах =
4 4 4
і
4 4 8-
1
х зіп2х х зіп4х ^ Зх зіп2х зіп4х „ .
= + —+ + С= + + С .
4 4 8 32 8 4 32
Приклад
25.
Знайти
1 = |
зіп
4
х
•
соз
5
х
сіх
.
•
/ =
|зІП
4
X
С05
5
X
СІХ
=
_[$ІП
4
Х(1
-5ІП
2
х)
2
СОЗХ СІХ
=
1 2 1
=
Г
5ІП
4
х(1
—
2
5ІП
2
Х +
5ІП
4
х) оїзіпх) =
—5ІП
5
Х
зіп
7
х
+
—5ІП
9
Х
+ С .
-
1
5 7 9
Приклад
26.
Обчислити інтеграл
/ = |
сіх
зіп
4
х
•
соз
2
X
•
Показники степенів - парні, від'ємні, тому застосуємо підстанов-
ку: (§ х = /. Тут також правомірне застосування правила /?(-зіп х,-соз х) =
= /?(зіп х, соз х), що веде до цієї ж підстановки.
СІХ
ЗІП Х-С05
X
І£Х=Г
х = агсі§ /
сіх
=
-
\+(*
-сі/
•
2 І
зіп
X
=
1+/
2
2
1
СОЗ X
=
-
1
+ Ґ
•\
+ 2і
2
+і
А
~
[—^т—[('~
4
+ 2Г
2
+1) аї =—тг-- +
г
+ С= І г = і§х
1
=
•'
г •' Зг г
1 1
= сІ§
3
х - 2 сІ§х + Щ х + С .<

44
Глава 1. Інтегральне числення функцій однієї змінної
Приклад 27. Знайти / = | зіп 2х
•
соз 5х сіх.
• До підінтегральної функції застосуємо формулу тригонометрії
зіп тх
•
соз пх = [ зіп(/и + п)х + зіп(/й - п)х ],
тобто
/ = |зіп2х соз5хйх =— |(зіп їх - зіп Зх)йх =
-соз7х + —созЗх \+С . ^
217 З
Приклад 28. Знайти / = | зіп 2х
•
соз 5х
•
зіп 9х
сіх
.
• / = |зіп2хсоз5х-зіп9хйх =
2|(зіп7х-зіпЗх)
5
І
п
9Х
ЙХ
=
= —|(зіп7х-зіп9х-зіпЗх- зіп9х) сіх =
=
— І (соз 2х - соз 16х - соз 6х + соз 12х) сіх =
1 ^зіп2х зіпібх зіпбх 5Іп12х^ „
=
—
+ +с =
4 2 16 6 12
\( . „ зіпібх зіпбх
5ІПІ2Х
. „ .
5іп2х + \+С .<
л/4
Приклад 29. Обчислити / = |
<іх.
• Для обчислення інтеграла застосуємо тригонометричну підстановку.
•соз
2
(СІІ „гі-зіп
2
/
х = 2 зіп/
ЙХ = 2 СОЗ/ЙЇ
сії
;
74^4зіп
2
/ „
= )
:
2соз/ сії ••
2
зіп/
= 2[ = 2[ й/ = 2[ 2[зіп / ої = 21п
•"зіп/
•* зіп/ зіп/
/
*2
+ 2соз/ + С,
• х .
де / = агсзіп—.
2
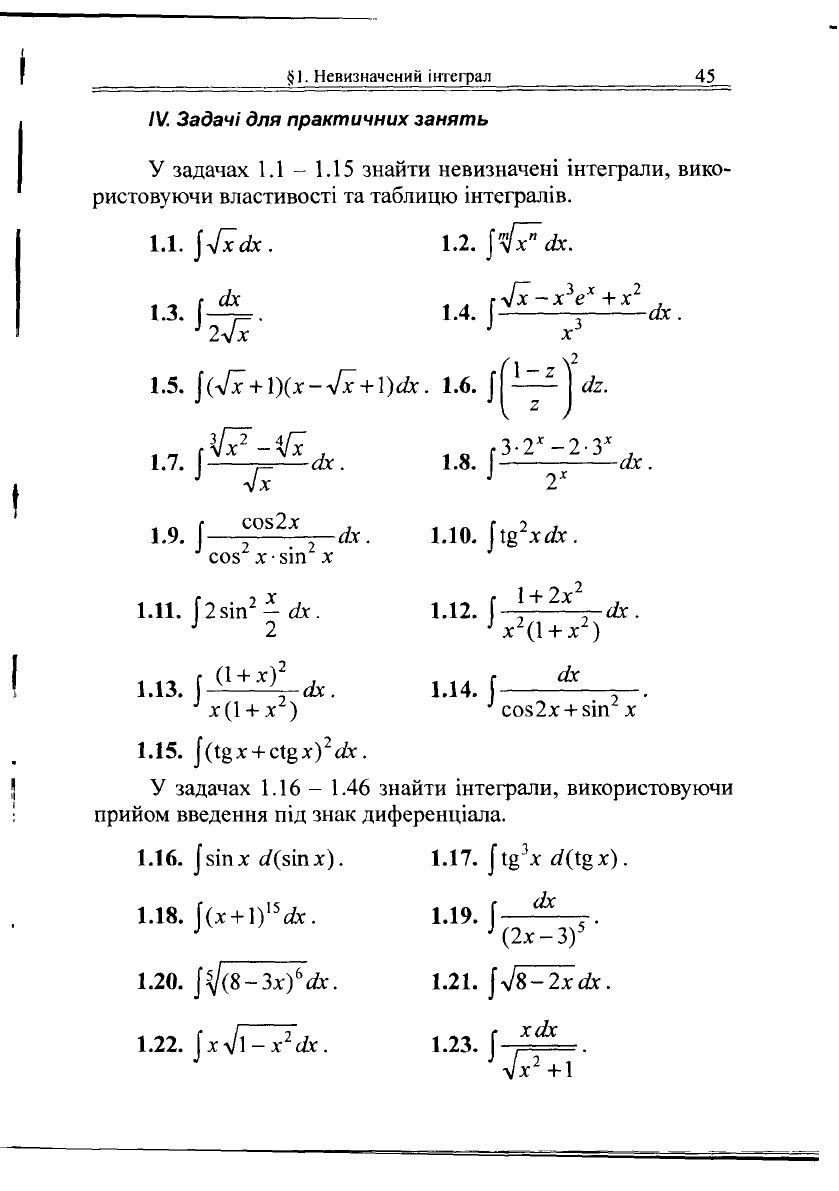
§1.
Невизначений інтеграл
45
IV.
Задачі
для
практичних занять
У задачах
1.1 - 1.15
знайти невизначені інтеграли, вико-
ристовуючи властивості
та
таблицю інтегралів.
1.1.
|л/хйх
сіх
1.2.
\Іх~"сіх.
1.3.
| *
1
24х
1.5. |(л/х + 1)(х-л/х + 1)йх. 1.6. \
*
.
ГУГх
-Х
2
Є* +Х
2
.
1.4.
] ^ сіх,
'1-2^
V
2
;
СІ2.
1.7. \И
ІЗ.
\
3/^2
4
Гх
соз2х
сіх,
ід.
гЗ-2"-2-3"
.І
ОХ
соз
2
х
•
зіп
2
х
#х. 1.10.
|і§
2
хй5с.
1.11. [2зіп
2
-
сіх.
}
2
1.13.
|
(1
+
х)
2
-сіх
1.12.
|
1.14.
|
1
+ 2х"
х
2
(1
+ х
2
)
ох
йх
соз2х
+
зіп
х
х(1
+ х
г
)
1.15. |(4§х
+
с1§х)
2
ах.
У задачах
1.16
- 1.46
знайти інтеграли, використовуючи
прийом введення
під
знак диференціала.
1.16. |зіпх а'(зіпх).
1.17.
|і§
3
х сі(Щх).
1.18.
[(х
+
1)
І5
ох.
1.19.
[—^-
т
.
-
1
\2х-з)
5
1.20.
|лУ(8-Зх)
6
йх.
1.22. |хл/і-х
2
с&. 1.23.|
1.21.
|л/8-2хох.
л/х
2
+Г
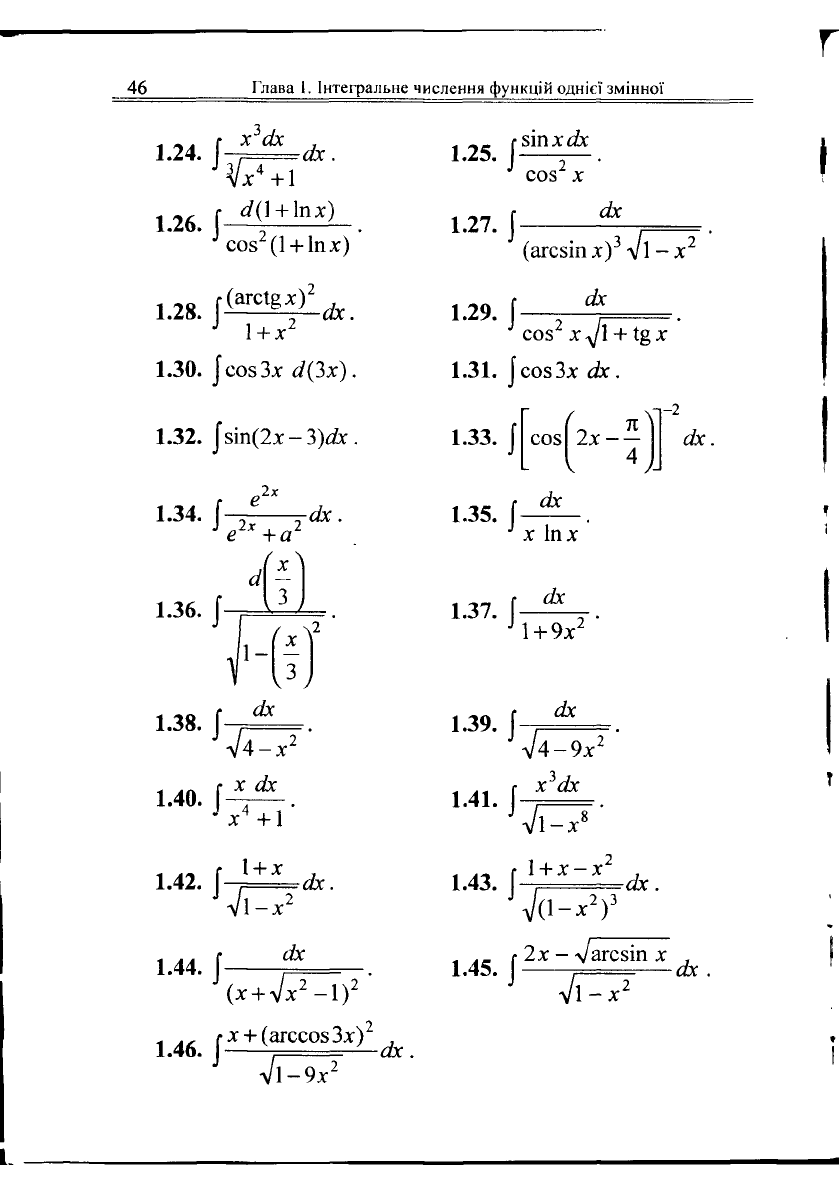
46
Глава
1.
Інтегральне числення функцій однієї змінної
1.24.
1.26.
1.28.
1.30.
1.32.
1.34.
1.36.
1.38.
1.40.
1.42.
1.44.
1.46.
X
сіх
сіх.
сі(]
+ \пх)
С05
2
(1
+
ІПХ)
(агсІ§х)"
сіх,
1
+ х'
созЗх
сі(3х).
зіп(2х
-
3)сіх.
„2х
е
2
*+а
2
•сіх.
1-
сіх
4^?
х
сіх
х
4
+1
1
+ х
V
•
СІХ.
\-х
1
сіх
(х
+
л/х
2
-1)
2
'
х
+
(агссозЗх)"
Л/І-9Х
2
сіх.
зіпхях
соз
2
X
сіх
(агсзіп
х)
3
Л/І
- X
і
сіх
1.25.
/
1.27.
\
1.29.
Г , ,
СОЗ Хд/1
+ ^Х
1.31. |созЗх
сіх.
1.33. [
С05І2Х-—
І сіх
1.35.
{
1.37.
\
1.39.
|
1.41.
\
1.43.
|
X
Іпх
сіх
1
+ 9х
2
ах
л/4-9х
2
х
3
<3х
1-х
8
1
+ х-х
2
л/0-^)
:
„
г
2х -
л/агсзіп
х ,
1.45.
, сіх

§1,
Невизначений інтеграл
47
У задачах
1.47 - 1.58
знайти інтеграли, виділивши "цілу
частину" підінтегрального дробу.
1.47.
1.48.
\^—ах.
^
х
+ 4
}
2х +
1
1.49.
[
—
сіх.
1.50.
\^Ч-сіх.
3
3-х
^
х-2
,
г
(1
+ х)
2
.
г
х
4
ох
1.51.
у
,
7
ох. 1.52. І .
}
х
2
+\
^
1-х
-.
^
гХ
5
+1
.
гХ
2
+Х
+
1
,
1.53.
— сіх. 1.54.
сіх
.
•"х
2
+4
-
1
х + 1
1.55.
[—^———#х. 1.56.
[
— -сіх.
}
х
2
+2х
+
2
}
2х + 1
1.57. \*
4
~:
2x2
~
]
сіх. 1.58.
і
2
**
+5
сіх.
}
х
2
+
1
* х-1
У задачах
1.59 - 1.80
знайти інтеграли, використавши при-
йом розкладу підінтегрального виразу
та
прийом виділення "пов-
ного квадрата".
^
тп
, сіх „ _ с сіх
.59.
[ . 1.60. [
Ч(х-1)
-
1
(х
+
1)(2х-3)
х
2
+1 , . _
г
ох
7х
+ 10
1.61.
Рт^-айс-
!-
62
-
;
х
2
-1
-
1
х
2
ЬбЗ.Г-—^
. 1.64. Г—^—.
•
|
х
2
+3х-10
^
4х
2
-9
1.65.
Г * . 1.66. Г * .
•Чх-1)
2
+4
>х
2
+2х +
3
1.67.
^ . 1.68. }- *
4х
2
+4х
+ 5' *
^\-(2х
+ 3)
2
1.69.
І * . 1.70. |-
Л
лМх-З-х
2
л/8
+
6х-9х
2

48
Глава
1.
Інтегральне числення функцій однієї змінної
СІХ
1.71. [-,
л/2-6х-9х
2
1.73. |
1.75. |
1.77. |
1.79. |
сіх
л/і2х-9х
2
-2
(х
+
2)сіх
X
і
+2х
+
2 '
(Зх-і)йх
л/х
2
+2х
+
2
(2х
+
5)сіх
1.72. |
1.74. |
йх
УІ5-- 2х + х
2
(8х-11)ах
лІ5 + 2х-х
2
(Зх-І)йх
1.76. Г-
Мх
2
-4х + 17
9х^+6х + 2
1.78. |
1.80. |
(х-2)йх
х
2
-7х + 12 '
(4-Зх)йх
5х
2
+6х + 18
У задачах 1.81 - 1.99 знайти інтеграли, застосовуючи від-
повідну заміну змінної.
1.81. \
4Х + З
^сіх.
1.82. [^5— сіх
1
х(х + 1)
(х-2)
сіх
1.83. [ , (підстановка х + \ = і
і
)
І+Ух+1
1.84. Г ^^ (підстановка х = г
6
).
ЛІХ -л/Х
Тх
1.85. |тт=^——я* (підстановка х =
2
12
).
З/
2 4/
Л/Х
- л/Х
1.86. \
е
2х
сіх
V771
(підстановка е
х
+ ).
1.87. сіх.
1.89. [
ХІПХ
ЙХ
1.88. |-
ІПІ§Х
зіп х
•
СОЗ X
•сіх
1+л/х+Т
(підстановка х +1 = г ).

§
1.
Невизначений інтеграл
49
сіх 1
1.90. [ , (підстановка х =
—,
або Х =
ЙІ§2,
або
х-азЬг).
1.91.
[
Х(
^
х
=
(підстановка Х =
Й§ІП2).
Л/Й
2
-х
2
.
м
г х сіх , . а .
1.92. —===== (підстановка х = ).
4х
2
-а
2
С08г
л
_„ г сіх , . 1 а
1.93. —. (підстановка х =
—,
або х = , або
х4х
2
-а
2 2 0082
йх , . 1 й
хл/
х = аспг).
1.94. | * 1.95. /-
Л
(1-Х
2
)^
Х
3
л/х
2
-1
1.96. 1^—. 1.97. |^ + со^
ф
.
хл/1 + х
2
л/х-8Іп2л/х
1.98. [-/——(підстановка х =
—).
V
Х +
1
X 2
1.99. |—===== (підстановка х =
зіп
2
2).
л/х - х
2
У задачах 1.100 - 1.120 інтегруванням частинами знайти
інтеграли.
1.100. ^x зіп2х сіх. 1.101.
|ХСОЗХЙХ.
1.102. \хе~
х
сіх. 1.103. \хУсіх.
1.104. |х агсІ§х сіх . 1.105. |іпхйх.
1.106. ^гхс\%хсіх. 1.107. |агсІ§л/х
ЙХ
.
1.108. \
аТ
^
тХ
сіх. 1.109. [агссозхйх.
}
УІХ
+ Ї
1

50
Глава 1. Інтегральне числення функцій однієї змінної
1.110. [ 1.111. \х
2
е-
х
сіх.
1.112. \х
г
е
х
сіх. 1.113. \х
2
а
х
сіх.
1.114. |(агс8Іпх)
2
ох. 1.115. |е*зіпхях.
1.116. |е
3
*(зіп2х-со82х)ах. 1.117. |зіп1пхах.
1.118. \ СОЗІПХЙХ. 1.119.
І
зіп
4х сіх.
1.120. |х
2
е*зіпхах.
У задачах 1.121 - 1.141 знайти інтеграли від дробово-ра-
ціональних функцій.
1.121. ( — . 1.122. (•
ХСІХ
(х + 1)(2х +
1)
'2х
2
-Зх-2
2х
2
+41х-91 , „ Г сіх
1.123. [ ^
™
Х
~
УІ
ох. 1.124. [ , ,
•'(х-1)(х + 3)(х-4) Чх
3
-7х
2
-3х
1.125.
[
х5
^
х4
~
8
ох.
1.126. (
х3
~
]
сіх.
х - 4х •' 4х - х
1.127. |-
32ХЙ
*
(2х-1)(4х
2
-16х + 15)
2
сіх
с(х
2
-3х
+ 2)йх
1.128. V-
1Л29
' 1
х •' х(х
2
+2х + 1)
1.130. а) [— 4^ ; б) [
А
ІХ
\
9
, сіх
}
х
3
+5х
2
+8х + 4 •
і
х
4
-5х
3
+6х
2
1.131./-^Ц-Л.
1.132. |
Х
^
х"-х^ ' (х + 2)
2
(х + 4)
2
