Тевяшев А.Д., Литвин О.Г., Кривошеєва Г.М. та ін. Вища математика у прикладах та задачах. Ч 2
Подождите немного. Документ загружается.


§2.
Визначений інтеграл. Невласні інтеграли
71
• Особлива точка х = 0 . При х
—>
+0 для знаменника підінтеграль-
ної функції маємо еквівалентну нескінченно малу:
Інтеграл |^т= =
о V*
]
сіх 3 т
= —х*
ах
теж збігається.
0 + 0
1
= — збігається. Тоді і заданий інтеграл
г х-1
Приклад 16. Знайти інтеграл І .— сіх або встановити
-і І/х
5
його розбіжність.
• На заданому проміжку інтегрування точка х = 0 — особлива, функція
/(х) = .— у цій точці необмежена. Маємо невласний інтеграл другого роду:
гх-1 , г х-1 , г х-1 ,
,— ах = ,— ах+ ,— ах.
!іГТ
Ш Ї\І7
Розглядаємо перший інтефал:
0-0
/ 2
-1 \х -1
5 Л
З _
Г
З
сіх- Зх
3
+
З 1
Цей інтефал розбіжний. Отже і заданий інтефал розбіжний. -4
Приклад 17. Дослідити на збіжність інтеграл
Г С08
2
X ,
, СІХ.
• Особлива точка х = 1. Представимо підінтефальну функцію у вигляді:
Дх) =
т
СОЗ X
1
СОЗ X
1
УГ7 (1-х)
1
/
3
•
1
1
Порівняємо заданий інтефал з інтефалом вигляду Г Ц- сіх, який
є збіжним, бо р = — <\. Згідно з фаничною ознакою порівняння, вихідний
інтефал є також збіжним, бо

Глава 1. Інтегральне числення функцій однієї змінної
со«"
х 1
Ііт
ЖГ7
ТГТ
=
со^і
>0
ч
1/3
(1-х)
Приклад 18. Дослідити на збіжність інтеграл
2
г
созх .
• Особлива точка х = 1. Заданий інтеграл є абсолютно збіжним, тому
що
С05Х
1 • • г сіх 3. •
.. і інтеграл І ,.. = —(х-1)
1 + 0
= — збігається. М
2
IV. Задачі для практичних занять
У задачах
1.211-1.231
обчислити визначені інтеграли.
1.211. \4ї+~х~ах.
о
і
1.213. \(е
х
-\)*е
х
с!х
1.212.
]
1.214.
|
1
+ 1§х
сіу.
сіх.
1.215.
|
хсіх
о(*
2
+1)
2
'
1.216.
І^-сіх
1.217.
]хе'
х
ііх.
1.218.
|
хсіх
я/зт х
4
е-1
1.219.
| х
3
зіп хсіх.
1.220.
11п(х +
1)
сіх.

§2.
Визначений інтеграл. Невласні інтеграли
73
„
. \4хсіх . г л/х _,
1.221. |- . 1.222. -т= сіх,
І
1
+ Х І л/х-1
1.223.
\-^=гс1х.
1.224.
[л/(1-х
2
)
3
ох.
1.225.
[
2
.
1.226.
[-^
{ х
2
- Зх + 2 2 2х^ + Зх - 2
1.227.1-^3-.
1.228.|
аСк
х
х + х
і :
0
(х-а)(х-2а)
%
сіх %
1.229. [ . 1.230. [соз
5
х-зіп2хах.
І/ 1+ созх і
1.231. | л/созх - соз
3
х
сіх
.
-Я
У задачах 1.232 - 1.240 обчислити невласні інтеграли з не-
скінченними межами інтегрування (або встановити їх розбіжність).
1.232. а,
7*;
б)/*.
-г-оо +со
1.233. а) \е~
ах
сіх (я>0); б) | хе~* ох.
о
о
.
ч7 2ЇА
+
Г сіх
1.234. а) | -
т
—; б) )
х
1
+Г ' 1 х
2
+2х + 2
*
ч
+
Г сіх
+
Г хах
1.235.а)
[-= ; б) г-
\
х
2
(1 + х) {(1 + х)
3
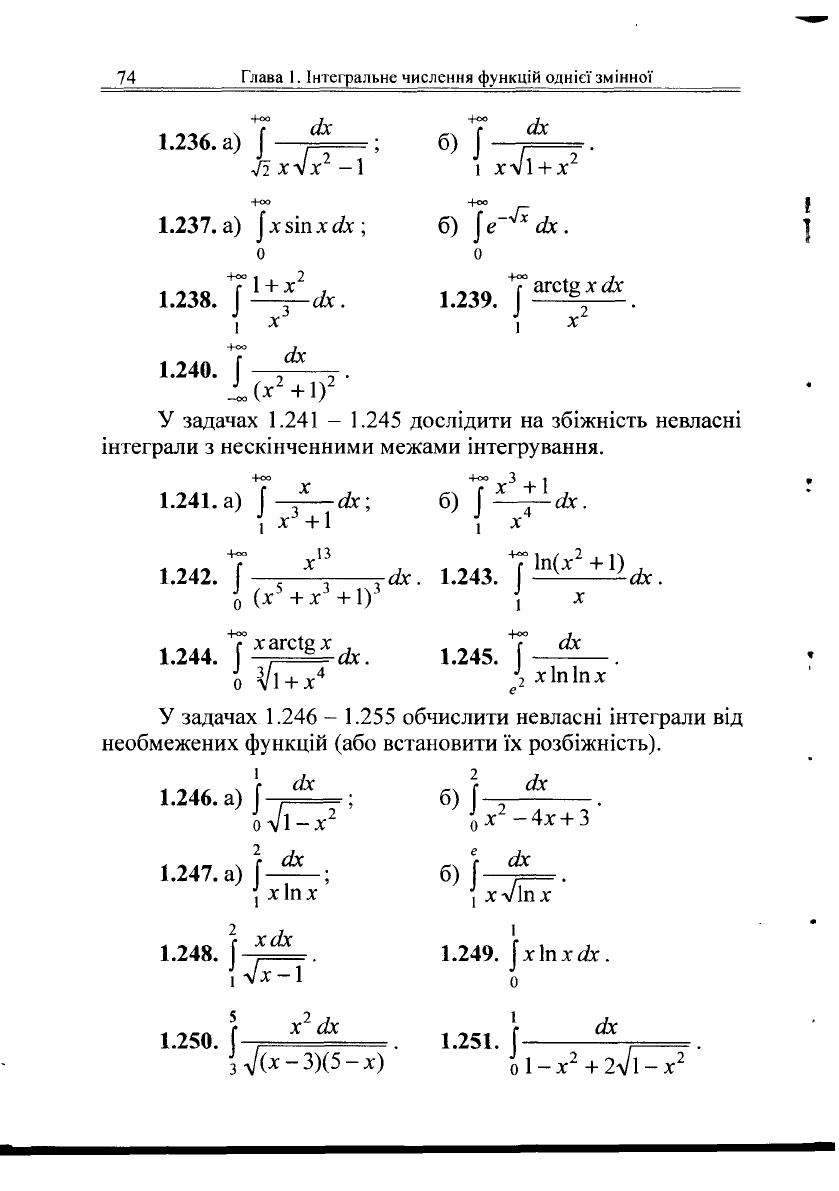
74
Глава
1.
Інтегральне числення функцій однієї змінної
СІХ "Т СІХ
4Ї
хл/х -1 і х\1 + х
1.237.
а) | х зіп хсіх; б) |е~^*ох.
о о
1.238.
і^сіх.
1.239.
1
1.240. \
Л
-і(*
2
+і)
2
У задачах 1.241 - 1.245 дослідити на збіжність невласні
інтеграли з нескінченними межами інтегрування.
1.241. а) \^—
сіх;
б)
\^р-сіх.
\
X
і
+\ і х
1.242. [—г-^Ц тих. 1.243. [
(Х + ]
сіх.
%
(х
5
+х
3
+ 1)
3
\ х
"Тхагсійх ,
ч
_._ *7 сіх
] .
6
сіх. 1.245. ] —
о
3
'
4
^і+ х
4
' ' *;
2
хіпіпх'
У задачах 1.246 - 1.255 обчислити невласні інтеграли від
необмежених функцій (або встановити їх розбіжність).
1.246.
а) ; б) ]
2
^
Іл/і^х
2
Іх
2
-4х + 3
ах ^
ч
г йх
1.247.
а) б)}-
,
х
1п
X і х
л/1п
X
2
ХЙХ
1
1.248. Г-^=. 1.249.
[ХІПХЙХ.
\у[х^ї
і
і .250. [ .
х2(к
. 1.251. [ *
^(^-ЗХЗ-х) о1-х
2
+2л/ї^с
Т
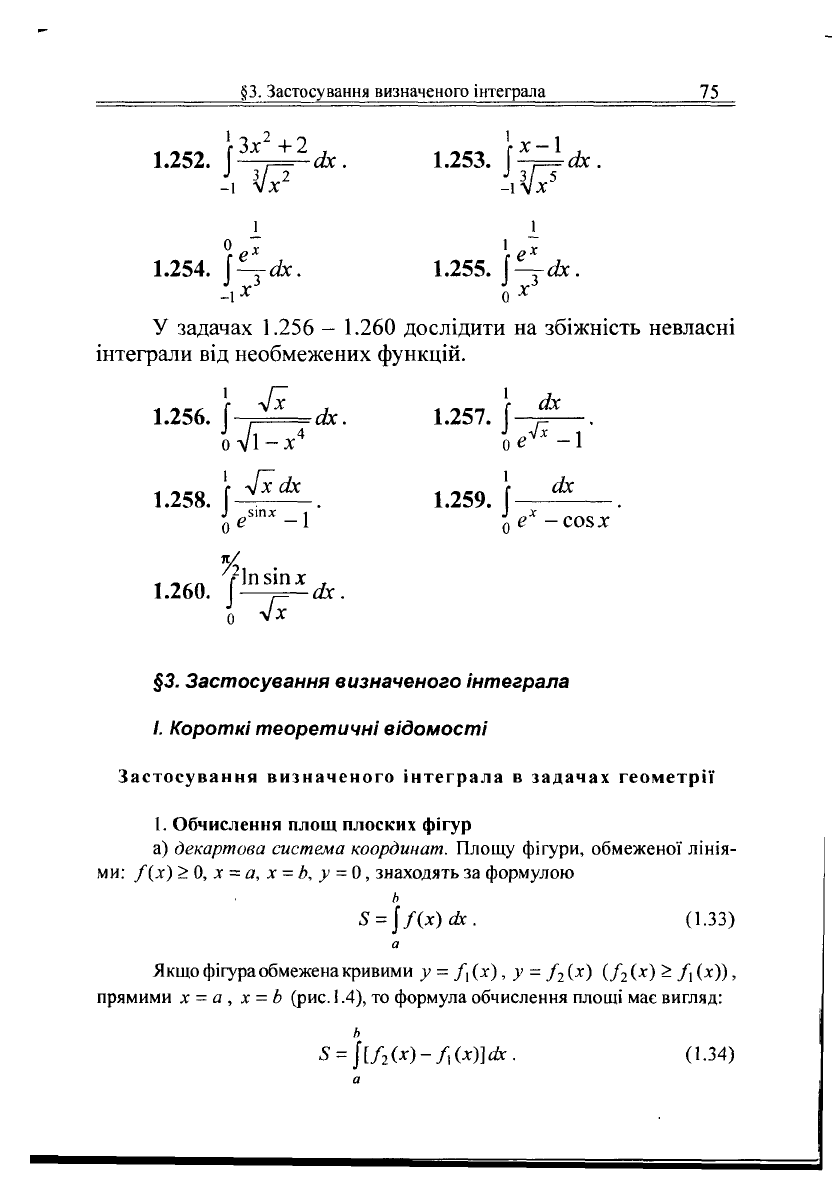
§3.
Застосування визначеного інтеграла
75
У задачах 1.256 - 1.260 дослідити на збіжність невласні
інтеграли від необмежених функцій.
§3. Застосування визначеного інтеграла
І. Короткі теоретичні відомості
Застосування визначеного інтеграла в задачах геометрії
1.
Обчислення площ плоских фігур
а) дексіртова система координат. Площу фігури, обмеженої лінія-
ми:
/(х) > 0, х = а, х = Ь, у = 0, знаходять за формулою
5 = \/(х)ах. (1.33)
а
Якщо фігура обмежена кривими у =
/|(х),
у = /
2
(х)
(/
2
(х)>
/і(х)),
прямими х - а , х = Ь (рис. 1.4), то формула обчислення площі має вигляд:
ь
5 = ІІ/г(х)-А(х)]<Ь- (1-34)
а

76
Глава
1.
Інтегральне числення функцій однієї змінної
О* а Ь х
Рис.
1.4
б) полярна система координат. Площа криволінійного сектора,
об-
меженого кривою, заданою
у
полярних координатах рівнянням
р = р(ф), і
двома променями
ф = а, ф =
(3
(а < Р),
обчислюється
за
формулою
5
=
-}р
2
(
Ф
)#.
(1.35)
в) якщо крива
у = у(х), х є [а, Ь]
задана параметричними рівняннями
Гх
=
*(/),
\у
= у(0,
а</<р,
причому
х(ос) = а, уф) = Ь , то
площа криволінійної трапеції, обмеженої
цією кривою, прямими
х = а, у = Ь і
віссю
Ох,
виражається формулою
х
= х(і),
у
= у(0,
8
=
\у(х)сіх=
ах =
х'(1)сІІ,
х
= а, / = а,
х
=
Ь,
/ = р.
де
а і 3
визначаються зрівнянь
а = х(а), Ь = хф) [у(і) > 0 при а < / < р].
Р
= ІУІ1)х\і)(&,
(1.36)
2.
Обчислення довжини
/
плоскої кривої
а) крива задана
у
прямокутних координатах рівнянням
у = /(х),
а<х<Ь:
ь
1
= \<£,
(1.37)
а
де
сі8 = ф + у'
2
ах -
диференціал дуги кривої;
б) крива задана
у
полярних координатах рівнянням
р = р(ф), а < ф < р :
Р
,
1
= \05, де
й?5
=
Л
/р
2
(ф)
+
р'
2
(ф)
<*р;

§3.
Застосування визначеного інтеграла
77
.
. .. \х = х(1),
в)
при
параметричному заданні кривої
< :
\у
= у(і),
а<і<$
Р
1
= ](Ш, де сі5 =
л]х'
2
(1)
+
у'
2
(1)
сії.
(1.38)
Довжину дуги гладкої просторової кривої, заданої рівняннями
х
- х(і),
•у
=
ЛО,
2
=
і(і),
а<?<р,
обчислюють
за
формулою, аналогічною формулі (1.38):
Р
1
= \4х'
2
(і) +
у'
2
(1)
+ 2
2
(1) Л.
(1.39)
3.
Обчислення об'ємів
тіл
а) об'єм тіла
за
площами паралельних перерізів обчислюється
за
фор-
мулою
ь
У=\$(х)сіх, (1.40)
а
де
5(х) -
площа перерізу тіла площиною, перпендикулярною
осі Ох,
а<х<Ь;
б) об'єм
тіл
обертання.
Об'єм тіла, отриманого
від
обертання криволінійної трапеції, обме-
женої кривою
у = Дх),
прямими
х = а, х
—
Ь, у = 0,
навколо
осі Ох,
вира-
жається формулою
п]у
2
(х)ах, (1.41)
а об'єм тіла, отриманого
від
обертання тієї
ж
криволінійної трапеції навколо
осі
Оу ,
обчислюється
за
формулою
ь
У
у
=
2к\ху(х)сіх
.
а
Аналогічно об'єм тіла, отриманого
від
обертання криволінійної тра-
пеції, обмеженої кривою
х =
ф(і'), прямими
у = с, у = сі, х = 0,
навколо
осі
Оу
,
знаходять
за
формулою
У
у
=п\х
2
(у)сіу.
(1.42)

78
Глава 1, Інтегральне числення функцій однієї змінної
Якщо фігура, обмежена кривими _у, = /\(х) і у
2
= /
2
(х)
[0</|(х) ^ /
2
(х)]
та
прямими х=а,х=Ь, обертається навколо осі Ох, то
об'єм тіла обертання
ь
У
х
=к\[/
2
2
{х)-/
2
{х)]ах. (1.43)
а
Для фігури, обмеженої кривими х
1
=ф,(>') і х
2
=<р
2
(у)
[0<ф,(>')<ф2(>')]
та прямими у=с, у=сі, яка обертається навколо осі Оу ,
формула об'єма тіла обертання має вигляд
</
У
у
=п\[^
2
{у)-^
2
{у)]ау.
с
Якщо криволінійний сектор, обмежений кривою р = р(ф) і променя-
ми ф, = а, ф
2
= Р , обертається навколо полярної осі, то об'єм тіла обертан-
ня визначається так:
2
Р
V =— л|р
3
зіпфаф. (1-44)
-
1
а
4.
Обчислення площі поверхні обертання. Нехай крива, задана не-
перервною функцією у = /(х) > 0, а < х < Ь , обертається навколо осі Ох .
Тоді площа поверхні, утвореної обертанням кривої у = /(х) навколо осі
Ох, знаходиться за формулою
ь
Р
х
=2%\у(х)Л8, (1.45)
а
де «"5 - диференціал дуги кривої.
Для кривої, заданої у прямокутних координатах, формула (1.45) має вигляд
Р
х
=
2л\у{х)4\+у'
2
ах; (1.46)
-
для полярної системи
Р
х
=2л|р5Іпф
А
/р
2
(ф)
+ р'
2
(ф)йф; (1.47)
а
•
якщо крива задана параметрично, то
Р
х
=2п]у(і)уІх'
2
(і) +
у'
2
(і)сІі.
(1.48)

§3.
Застосування визначеного інтеграла
79
Застосування визначеного інтеграла в задачах фізики
1.
Маса неоднорідного стрижня, розташованого на відрізку [а, Ь],
якщо лінійна густина стрижня дорівнює р(х), обчислюється за формулою
ь
м = |рО)<&.
а
2.
Статичні моменти М
х
, М
у
та моменти інерції
І
х
,І
у
плоскої
кривої у = /(х) обчислюються за формулами:
* ь
а) відносно осі Ох: М
х
= ]усі8, І
х
= |у
2
сі8 ,
а а
Ь Ь
б) відносно осі Оу : М
у
= ^хсі8, І
у
=
\х
2
сБ,
а а
де сІ8 = \\\ + у'
2
сіх - диференціал дуги кривої.
3.
Статичні моменти та моменти інерції криволінійної трапеції,
обмеженої кривою у = /(х), прямими: у = 0, х = а, х = Ь , обчислюються за
формулами:
1 * 1 * 1
Л
а) відносно осі Ох : М
х
=—^усЕ-—^у
2
сіх, І
х
=—|у
3
Л;
а а а
Ь Ь Ь Ь
б) відносно осі Оу : М
у
= ^хсі8 = ^хусіх, 1
у
= |х
2
аК = ^х
2
усіх.
а а а а
У цих формулах сі8 = усіх - диференціал площі криволінійної трапеції.
4.
Координати центра ваги:
а) плоскої кривої у = /(х) (о < х <Ь)
І, .„ і"
х
с
=-\хсі8,
Ус
=-\усі8,
де / - довжина кривої, сі8 - диференціал дуги кривої;
б) криволінійної трапеції
1 * 1 *
х
с
=-\х<&,
Ус
=—\усі8,
а а
де сі8 = уск, 8 - площа фігури.

80
Глава 1, Інтегральне числення функцій однієї змінної
Мають місце такі теореми.
Теорема (перша теорема Гульдіна). Площа поверхні обертання, яка
утво-
рюється від обертання дуги АВ навколо осі, що її не перетинає і розташована в
площині дуги АВ, дорівнює добутку довжини кола, яке отримується від обер-
тання центра ваги дуги АВ навколо цієї осі, на довжину 1
АВ
дуги АВ.
Якщо віссю обертання є вісь Ох, відповідна формула має вигляд:
?х = 2пу
с
1
АН
.
Теорема (друга теорема Гульдіна). Об'єм тіла обертання, яке утворю-
ється від обертання плоскої області £> навколо осі, що її не перетинає і розта-
шована в площині області О, дорівнює добутку довжини кола, яке отримується
від обертання центра ваги області £> навколо цієї осі, на площу 8
0
області О.
Якщо віссю обертання є вісь Ох, відповідна формула має вигляд:
У
х
=2ку
с
8
а
.
5.
Обчислення роботи. Робота змінної сили Р = Р(х), яка діє у на-
прямку осі Ох на відрізку [а, Ь], визначається формулою
*
А = \р(х)ах. (1.49)
а
6. Довжина шляху 5, який проходить матеріальна точка, що рухаєть-
ся зі швидкістю у = У(І) за проміжок часу [/, ,і
2
], обчислюється за формулою
'2
ч
II. Контрольні питання та завдання
1.
Як обчислити площу плоскої фігури при різних формах
її задання?
2.
Як обчислити довжину дуги кривої:
а) у декартовій системі координат?
б) у полярних координатах?
в) у випадку, коли крива задана параметричними рівняннями?
3.
Наведіть формулу для обчислення об'єму тіла за площа-
ми його паралельних перерізів.
