Тевяшев А.Д., Литвин О.Г., Кривошеєва Г.М. та ін. Вища математика у прикладах та задачах. Ч 2
Подождите немного. Документ загружается.


§3.
Застосування визначеного інтеграла
81
4.
Наведіть формули для об'ємів тіл обертання: навколо
осі Ох, навколо осі Оу,
5.
Запишіть формулу для обчислення площі поверхні обертання.
6. Як знайти масу неоднорідного стрижня?
7.
За якими формулами знаходяться координати центра
ваги: а) плоскої кривої; б) криволінійної трапеції?
8.
Запишіть формулу для обчислення роботи змінної сили ¥{х).
III. Приклади розв'язання задач
У цьому пункті розглянуто ЗО прикладів розв'язання за-
дач,
які за своєю тематикою розподілились так:
1.
Обчислення площ: приклади 1-6.
2.
Обчислення довжини дуг: приклади 7-11.
3.
Обчислення об'ємів тіл за площами паралельних пере-
різів:
приклади 12, 13.
4.
Обчислення об'ємів тіл обертання: приклади 14-17.
5.
Обчислення площі поверхні обертання: приклади 18, 19.
6. Обчислення статичних моментів, моментів інерції, коор-
динат центра ваги кривої та плоскої області: приклади 20 - 23.
7.
Різні фізичні задачі: приклади 24 - ЗО.
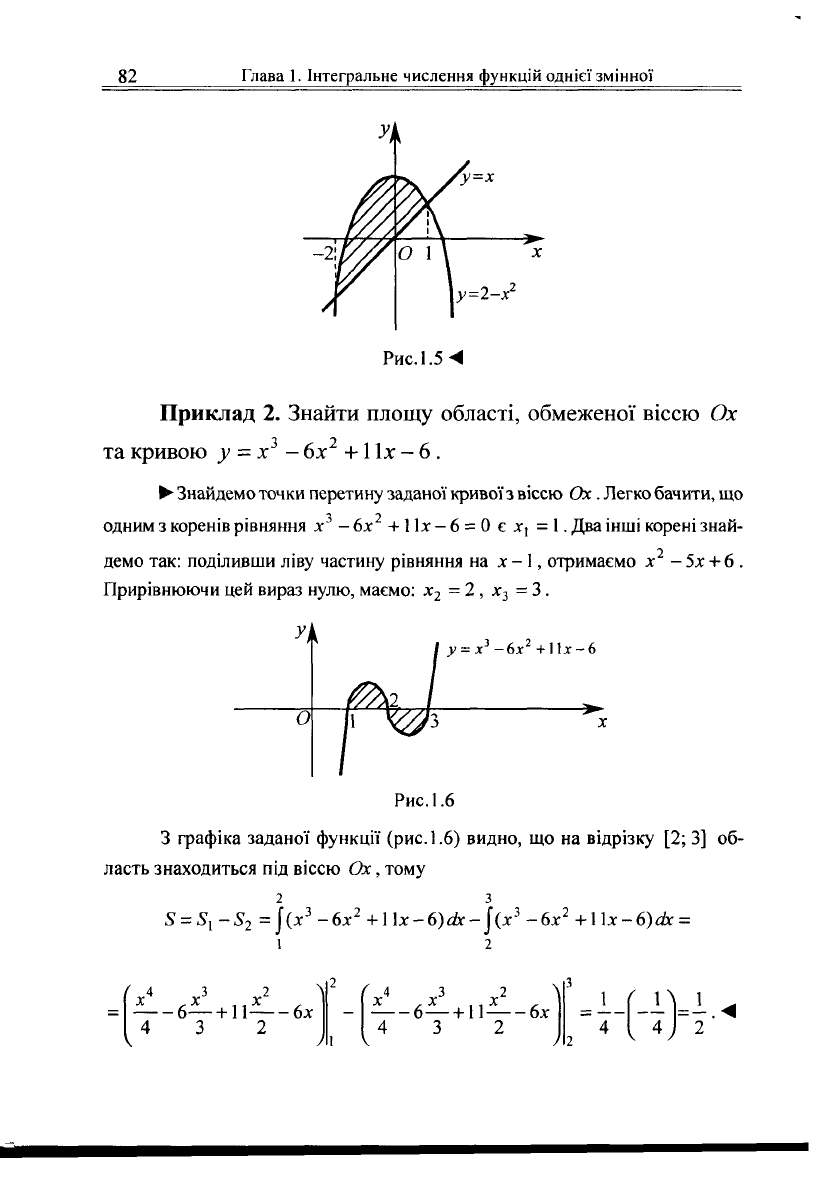
Приклад 1. Обчислити площу області, обмеженої прямою
у = х та кривою у - 2-х
(рис.
1.5).
З цієї системи дістанемо Х\ = -2, х
2
= 1. Це і є межі інтегрування. За
формулою (1.34)
• Знайдемо абсциси точок перетину даних ліній:
ь
Я
= /[/
2
(*)-/,(*)]<&
а
знаходимо площу 5 = |[(2-
х
2
)-х]ах =
2х
~^~~~^
V ) -2
82
Глава 1. Інтегральне числення функцій однієї змінної
Рисі.5 4
Приклад 2. Знайти площу області, обмеженої віссю Ох
та кривою у = х
3
- 6х
2
+1 їх - 6 .
• Знайдемо точки перетину заданої кривої з віссю Ох. Легко бачити, що
З 2
одним з коренів рівняння х -6х +1ІДГ
—
6 =
0єдГ)=1.
Два інші корені знай-
демо так: поділивши ліву частину рівняння на х-1, отримаємо х
2
-5х + 6 .
Прирівнюючи цей вираз нулю, маємо: х
2
= 2, х
3
= 3.
у,
к 3 2
/ у = х
3
-6х
2
+1ІХ-6
О
Рис.
1.6
З фафіка заданої функції (рис. 1.6) видно, що на відрізку [2; 3] об-
ласть знаходиться під віссю Ох, тому
2 З
5 = ^ -5
2
=|(х
3
-6л:
2
+ \\х-6)ах-\(х
г
-6х
2
+\\х-6)ах
=
( 4 3 2 \
-—6—
-ь 11——6х
4 3 2
V ^
(
— -б— + 11 —
-бд:^
4 3 2
V

§3.
Застосування визначеного інтеграла
83
Приклад 3. Знайти площу фігури, обмеженої кривою
р
2
=а
2
со§2ф (лемніската Бернуллі).
• Крива задана у полярній системі координат (рис. 1.7)
4
Рис.
1.7
Має місце формула (1.35):
5 = -|р
2
(ф)аср.
Оскільки фігура симетрична відносно обох осей, то шукана площа
дорівнює почетвереній площі фігури, яка знаходиться у першій чверті.
я я
При ф] = 0 р = а, при р = 0 ф
2
= —, тобто 0 < ф < —.
4 4
Маємо
5 = 4—|а
2
соз2фо'ф= 2а
2
|соз2фй?ф= 2а
зіп2ф
4
= а\<
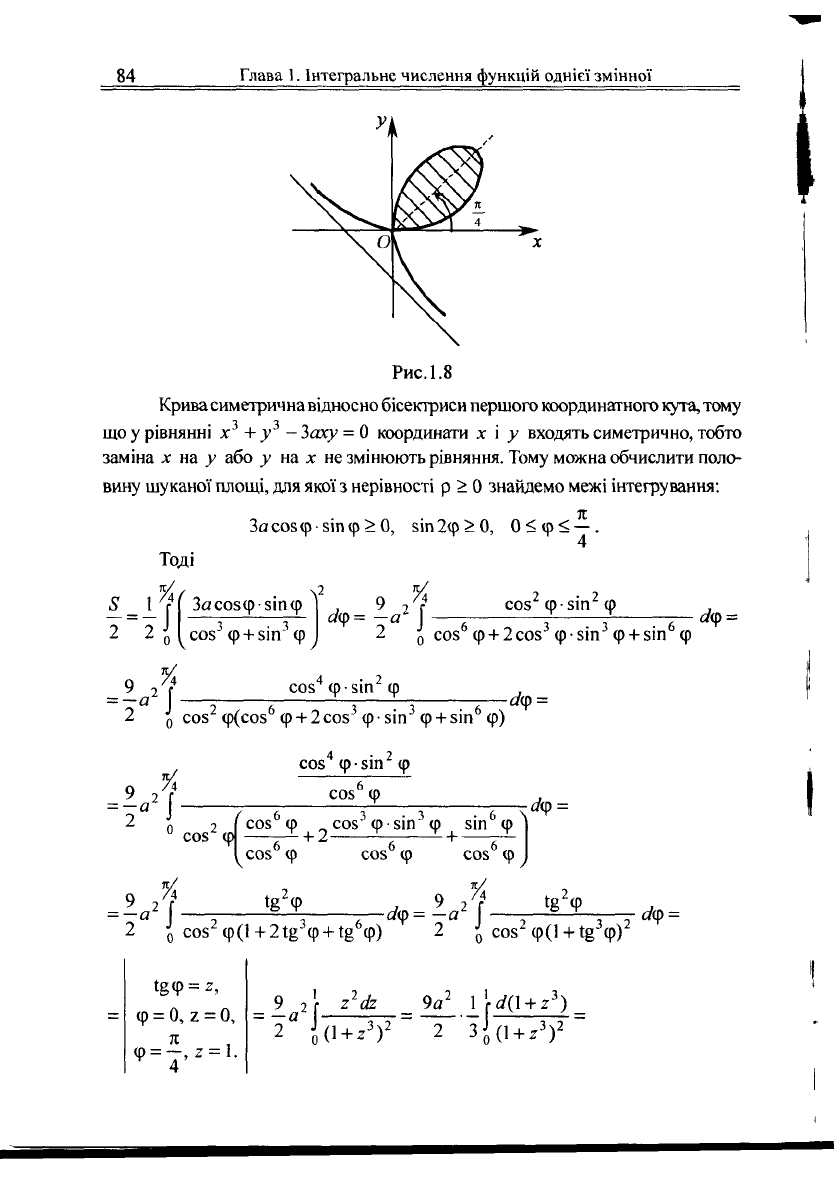
Приклад 4. Обчислити площу фігури, обмеженої петлею
декартова листа, заданого рівнянням х
3
+ у
3
- Зассу = 0
(рис.
1.8).
• Перейдемо до полярної системи координат: х = рсозф, _у = рзіпф.
Маємо:
Звідси р =
р
3
(соз
3
ф + зіп
3
ф)-3ар
2
созф-зіпф = 0.
Засозф-зіпф
соз
3
ф + зіп
3
ф
84
Глава 1. Інтегральне числення функцій однієї змінної
Рис.
1.8
Крива симетрична відносно бісектриси першого координатного кута, тому
що у рівнянні х
3
+ у
3
-Заху = 0 координати х і у входять симетрично, тобто
заміна х на у або у на х не змінюють рівняння. Тому можна обчислити поло-
вину шуканої площі, для якої з нерівності р > 0 знайдемо межі інтегрування:
Тоді
3асозф-зіпф>0, зіп2ф>0, 0<ф<—.
4
і> _ 1 г
ЗаСОЗф-ЗІПф
2 2
9
СОЗ
3
ф +
5ІП
3
ф
9 . %
СОЗ
2
ф-5ІП
2
ф
СЛР
=
2 і
соз
6
ф
+
2соз
3
ф-ЗІП
3
ф
+
8ІП
6
ф
соз
4
ф-зіп
2
ф
соз
ф(С05
ф + 2соз ф•
ЗІП
ф +
ЗІП
ф)
І
У,
у
І-
соз
4
ф-ЗІП
2
ф
соз
6
ф
(
0
соз
2
ф
СОЗ
ф
СОЗ"
ф-
ЗІП
ф 51П ф
СОЗ
ф СОЗ ф СОЗ ф
ГІФ
:
о /}
2 І соз
2
ф(1 + 2іе ф + І8 Ф)
9 /4
<Лр=-а
2
\
соз
2
ф(1 + Іі
3
ф)
2
СЛР
=
ЧЗФ=2,
ф = 0, 2 = 0,
ф = -,2 = 1.
4
9 2Г ^
9а
2
_
1_',</(!+
г
3
)
2 3^(1
+ г
3
)
ЗЧ2

§3.
Застосування визначеного інтеграла
85
За
1
За'
о
Л
а
2
4
3
2 3
2
Остаточно
5 =
2— а
=—
а
.-4
4
2
Приклад
5.
Знайти площу фігури, обмеженої еліпсом
х
=
асо$1,
у = Ь§'т(, 0<ґ<2к.
• Крива задана параметрично, скористаємось формулою (1.36):
х =
х(і),
У =
У((),
5
=
\у(х)сіх
=
сіх
=
х'(і)Ж,
=
$ у(і)х'(і)сіі
х =
а, і = а,
х = Ь,
/ =
[3.
Оскільки фігура симетрична відносно обох осей,
то
шукана площа
дорівнює почетвереній площі фігури, розташованій
у
першій чверті.
Тому:
5
=
4\у(х)ах
=
х
=
а сох/,
у =/>5ІП/,
ах
=
—а%тіЖ,
*
=
0,
, = §,
х
= а, /=0.
о
о
-4 |б5Іпг- азіп/
аї = -4аЬ
[кіп
2
/аї =
=
2аЬ |
(1
+
соз 21) сії
=
2а6
/ + -
зіп 21
•
паЬ. -4
Приклад 6. Обчислити площу фігури, обмеженої петлею
лінії:
х = 3ї
2
, у =
1(3-I
і
).
•
3
параметричних рівнянь видно,
що
крива симетрична відносно
осі
Ох,
тому визначимо межі інтегрування для половини площі. При
/] = 0:
х
= 0 і у = 0, при
1
2
=4з
: х = 9 і у = 0,
тобто
0 < І < -\/з .
Отже
5
= 2 |
І(3-І
2
)6ІСІІ
=
П
\(3і
2
-1
4
)Л=
12
о
о
5
V
У

86
Глава 1. Інтегральне числення функцій однієї змінної
у>0.
Приклад
7. Знайти довжину кривої у
2
= х
3
(0 < х < 1),
).
•
Скористаємося формулою
(1.37)
для обчислення довжини кривої
/
= |Л/І + /
2
СІХ.
Враховуючи, що у = \1х
г
, у' = —х
2
, маємо
9 З
1+
—
х
4
27
11
Ч
4
У
27
27 8
Приклад
8. Знайти довжину дуги кривої у =
1п
х від точ-
ки
з абсцисою х, =
1
до точки з абсцисою х
2
•
Оскільки і> =
1п
х, у' = — ,то
X
і
V х і х
х = Щг,
ск
СОЗ
2
X
=1, 2
••
X
=
л/3,
2 -
К
4''
п
1^
%,
....
1§ 2 СІ2
£2
СОЗ 2
ск
ЗІП
2
• СОЗ
2
•І
СОЗ
2
ЗІП
2
СОЗ
2
-
+ ІП
%
• 2 2
г
ЗІП 2
+СОЗ
2^
тг/
ЗІП
2
•
СОЗ
2
2
3
г- 1 к
=
2 -
л/2
+ Іп-рг - 1п Іе-=
£
л/3 8
4
=
2-Л/2--1ПЗ-1ПІЄ-.4
2
8
Приклад
9.
Знайте довжину кардіоїди
р = а(1 + соз
ф)
(рис.
1.9).
•
Для обчислення довжини лінії, заданої у полярній системі коорди-
нат, має місце формула
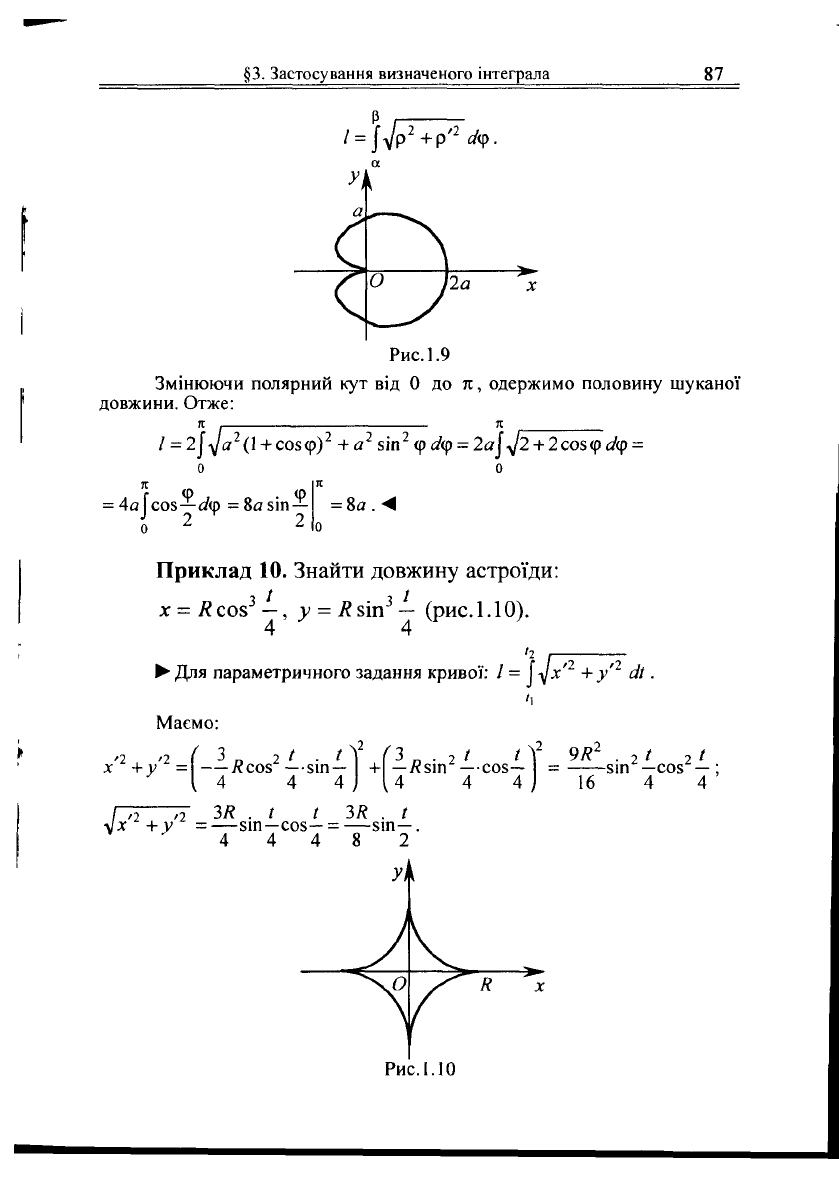
§3.
Застосування визначеного інтеграла
87
Р
,
1 = ^р
2
+р'
2
*ф.
у,
'
,
0
І2а
^
X
Рис.
1.9
Змінюючи полярний кут від 0 до л, одержимо половину шуканої
довжини. Отже:
7С . Л
/
= 2|-у/й
,2
(1 + со5ф)
2
+а
2
зіп
2
ф#ф = 2а[
>
/2 + 2созфа'ф =
4а|со5—йф
= 8а зіп — :8а.^
Приклад
10. Знайти довжину астроїди:
х
= К соз
3
—, у = Я зіп
3
—
(рис.
1.10).
4
4
•
Для параметричного задання кривої: / = $4х'
2
+ у'
2
Ж
•
'і
Маємо:
'2
а (3 _
2
/ - О
2
X
+
V
= /?С05
—ЗІП —
І
4 4 4 )
ГТ
2
а ЗЛ . / І ЗК . і
л/Х +у =
$1П —
СОХ—
= 51П—.
4 4 4 8 2
(1
п • 2 ( О
-
—кзіп —соз—
и
4 4]
2
9Р
2
.
2
/
зіп —соз —;
16 4 4
Рис.1.10

Глава
1.
Інтегральне числення функцій однієї змінної
Довжину чверті астроїди знаходитемо
від
точки
Л(К, 0) до
точки
6(0, К)
Тоді
і
І
при
х, = /?
маємо:
К =
Лсоз
—, = 0 ;
при
х, =0:
Лсоз
3
—
= 0,
—
= —, =2п.
4
4 2
ЗК
2к
( і
Отже,
1-А—
[зіп
—
сії
= -ЗК
соз
—
2л
= -ЗД(-1-1)
= 6Я .<
Приклад
11.
Знайти довжину гвинтової
лінії:
х-асозі,
у = а5'т(, г = с(.
• Скористаємось формулою (1.39)
для
просторового випадку:
1
= )4х'
2
+у'
2
+2
2
Сії.
а
Довжина лінії
від
точки
А (1 = 0) до
точки
М (і -
будь-яке) буде
/ =
І\/а
2
5Іп
2
/ +
а
2
со5
2
/
+ с
2
Ж =
^4а
2
~+с
2
сії
=
\[а
2
+~с
2
І. <
2
2 2
л
V 2
Приклад
12.
Знайти об'єм еліпсоїда
—г-
+ ~ + — = 1
а
2
Ь
2
с
2
• Скористаємось формулою (1.40):
Рисі.11

§3.
Застосування визначеного інтеграла
89
У перерізі еліпсоїда (рис. 1.11) площиною, паралельною площині Оуг
на відстані х від неї, утворюється еліпс (х =соп$і)
Ь
2
с
2
або
а
1
х
1
X
і
з півосями Ь
х
= й
Л
|І —, с, = с,|1
—
.
а V а
Площа такого еліпса (приклад 5) дорівнює
8{х) = пЬ
х
с
х
= пЬс
а
Отже,
К = пЬс ]
( х
2
]
а
Г
( х
2
]
' X
і
\
ах = 2лос
1 г
сіх = 2л6с
1 "
2
\
^
0
і а
2
}
-каЬс.
о
Зокрема, якщо а = Ь = с = К , то еліпсоїд перетворюється в кулю,
4
об'єм якої V = —пК . «4
З
Приклад 13. Знайти об'єм тіла, обмеженого двома пря-
9 9 9 9 9 9
круговими циліндрами: х
+
у = Я їх + 2 = Я .
• У перерізі тіла площиною, перпендикулярною осі Ох, маємо квад-
рат, сторона якого дорівнює у = V К -х .площа якого
5(х) = у
2
= К
2
-х
2
.
На рис. 1.12 зображена восьма частина тіла.
21
Рисі.12

90
Глава
1. Інтегральне числення функцій однієї змінної
Маємо:
У = 8|(Л
2
-= 8
(
у
.з^
з
Приклад 14. Знайти об'єм тіла обертання, утвореного обер-
танням параболи у = х
2
на проміжку
1
< х < 2 навколо: а) осі Ох,
б) осі Оу.
•
а) за формулою (1.41):
ь
У
х
= к^у
2
(х)ах (у нашому випадку у
2
=х
4
)
а
2
5
знаходимо
У
х
= я|л"
4
а!х-= л—
1
5
б)
за формулою (1.42): У
у
= п^х
2
(у)ау (х(у) = л/у )
4
2
маємо
У
у
=%^уау-к
—
ЗІТС
5
15л
Приклад 15. Фігура, обмежена кривими у =
л]2рх
і
2 V
у =
—т=
(х - р)
п
, обертається навколо осі Ох
(рис.
1.13).
Знай-
УІР
ти об'єм тіла обертання.
•
Знайдемо точку перетину заданих кривих:
/
2 У
^2рх
= —=•(*
—
ру
2
=>х = 2р, у = 2р.
ЛІР
2
V
