Тевяшев А.Д., Литвин О.Г., Кривошеєва Г.М. та ін. Вища математика у прикладах та задачах. Ч 2

Подождите немного. Документ загружается.

§3.

Теорія поля

271

Знак перед кожним інтегралом вибирається таким, який знак у відпо-

відного напрямного косинуса нормалі до поверхні о .

Якщо поверхня задана рівнянням Р(х,у,г) = 0, яке однозначно

розв'язується відносно будь-якої змінної, то це означає, що поверхня взаєм-

но однозначно проектується на відповідну координатну площину. Тоді для

обчислення поверхневого інтеграла, що виражає потік, використовується

метод проектування на одну координатну площину (див. глава 4, §2). Від-

повідні формули мають вигляд:

ДО(5,Й)Л=

(а,п)

або

^,со8а|

Я(

,я)*=

Ягіп

Я(з,й)*=

}}Ш

ауск

х=дг(у,г)

йхаг

ахау.

:=2(дт,у)

6. Якщо поверхня а не має взаємно однозначних проекцій на коор-

динатні площини, то цю поверхню розбивають на частини, які задовольня-

ють умовам взаємно однозначного проектування, а потім використовують

властивість адитивності поверхневих інтегралів.

Приклад

Обчислити потік векторного поля

= (х

г)і + (2у - х)і

гк

через зовнішню сторону поверхні

піраміди,

яка

утворена

пло-

щиною

х -2у + 2г = 4 і

координатними

площинами,

за

допо-

могою формули Остроградського-Гаусса.

•

За формулою Остроградського-Гаусса

Я(

-,Я)*

^аа-У

=і

%у.

Маємо Р(х,у,г) = х + г, 0,(х,у,г)=2у-х, К(х,у,г) = г,

дР . дС; дР .

—

= 1, — = 2 , — = 1,

СІІУ

а = 4.

дх ду дг

Тоді П =

Я(5,й)йго"

= Я/

^^ , де С - задана піраміда.

272

Глава 4. Криволінійні інтеграли. Поверхневі інтеграли. Теорія поля

Перетворимо рівняння площини х-2>> + 22 = 4 до вигляду

хуг

—+ —+ —

4-2 2

мокутний трикутник з катетами довжиною 4 та 2 відповідно.

пір ос

" 3 2 З

- + +

—

= 1. Звідси видно, що висота пірам іди

пір

= 2, а основа - пря-

Обчислимо об'єм піраміди: У

—

пір

жи

— •

•

8 32

Остаточно П = 4

• —

= —.

З З

Приклад

Обчислити потік векторного поля

а = хі + у) + гк

через зовнішню сторону бічної поверхні

циліндра

+ у

= К

обмеженого площинами

і = 0 і і = Н (Н > 0).

• Доповнимо задану поверхню о до повної поверхні площинами

2 = 0 і г = Н.

Тоді П = П

бічн

+П,+П

де П - потік через повну поверхню циліндра, П

бічн

- потік через бічну

поверхню, П]

—

потік через верхню основу циліндра, П

- через нижню.

Звідси П

6ІЧН

=П-П,-П

Потік через повну замкнену поверхню обчислимо за допомогою фор-

мули Остроградського-Гаусса

П =

\\\йі\асІУ.

Маємо Р(х,у,г) = х,

(2(х,у,г)

= у, Я(х,у,г) = г,

дх ду дг

п = Л|з^ =

зг

цилін

ЗпЯ

Н.

П, =

Д(5,Й)йго-

^(а,к)сіа = \\г\

:=н

сі<5

= Н^сіо = Яо, =

НпЯ

о, о, о, о,

=\\(а,п)сіо

=~\\(а,к)ііа

=-\\г\_

сі<5

= -||0^о = 0.

СТ

С, О]

Остаточно П

бічн

ЗкЯ

Н-кЯ

Н =

2кЯ

Н .<

§3. Теорія поля

273

Приклад

Обчислити потік векторного поля

= х

/ + .у

/ + 2

і— • 2 2 ^

через зовнішню сторону бічної поверхні конуса

х + у =

—2~

(0 < 2 < Я) .

• Доповнимо бічну поверхню конуса до повної замкненої поверхні

ПЛОЩИНОЮ

2 = Н .

Тоді П = П

бічн

+П

0СН

де П - потік через повну поверхню конуса, П

бічн

- потік через бічну поверх-

ню,

осн

- потік через основу.

Звідси П

бічн

= П-П

осн

За формулою Остроградського-Гаусса

Я(

,Я)*=№іу5^=Ш(^^

+ ^-

Маємо Р(х,у,г) = х

, 0(х,у,г) = у

, К(х,у,і) = 2

|Р

=3х

ад

,аІУа

3(х

ас сіу дг

С - замкнена область: х

+у

= ——г

, 0<г<Н .

Тоді

П =

зД[(х

+ у

+ г

)

сйгфаЬ =

Н'

= рС05ф,

7 = р8ІПф,

2 =

С': 0 < р < Я,

0 < ф < 2я,

уу

ахауаг =

рфс/фй

—р<г<Н.

2к К Н

= 3|||(Р

)рфй?ф^2=

3|й?ф|рф

|(р

)й2

0 0 «

= 3-2я[р

рг+

= 6л|

ТР"

~Р

Нл 1 //^

Ф =

= 6п(-Я

Н+-Я

--Я

Н-—Я

—пЯ

Н(Я

+2Н

^4 6 5 15 ; 10

274

Глава 4. Криволінійні інтеграли. Поверхневі інтеграли. Теорія поля

Тепер обчислимо потік через основу П

осн

безпосередньо.

осн.

= \\{а,п)сіо.

Рис.4.14

Оскільки потік обчислюється через зовнішню поверхню, то нормаль

п до основи конуса співпадає із вектором к (рис.4.14), отже,

П=к

=(0,0,1), (3,«)=2

-1 =2

, „2

Основою конуса є круг х + у < К , що розташований в площині

;

Пр

х()у

жи

°ху , &ху X

+ у

< К

ОТЖе,

осн

. = \\{а,п)4о =

\\г

0а

= Д*

| скау = Я

\\ахау= Я

тіЛ

"осн

Остаточно

,ліу2ч ігЗ„

г,2,

бічн.

П-П

осн

=—кК*Н(К

+2Н

)-Н

пК

=— /ГЯ(ЗЛ"-4Н

).<

10 10

Приклад

8. Обчислити потік векторного поля

= гі —хі + ук

через

нижню сторону

трикутника, отриманого

від перетину

пло-

щини

Зх + 6у - 2г = 6 з координатними площинами.

•

Задану поверхню зображено на рис.4.15.

Рис.4.15

§3.

Теорія поля

275

Наведемо

три

способи розв'язання задачі.

Спосіб

Доповнення незамкненої поверхні

до

замкненої.

Задана поверхня

трикутник

незамкнена. Доповнимо

її до

замк-

неної. Разом

координатними площинами площина

Зх +

6у-2г

= 6

утво-

рює замкнену поверхню

поверхню піраміди. Позначимо

її о,

тобто

ст:

хуг,

1 -3

= 0, у = 0, 2 = 0.

РЮу°=°ху>

Рю^ =

°х

> ПРуОг

а=£)

уг

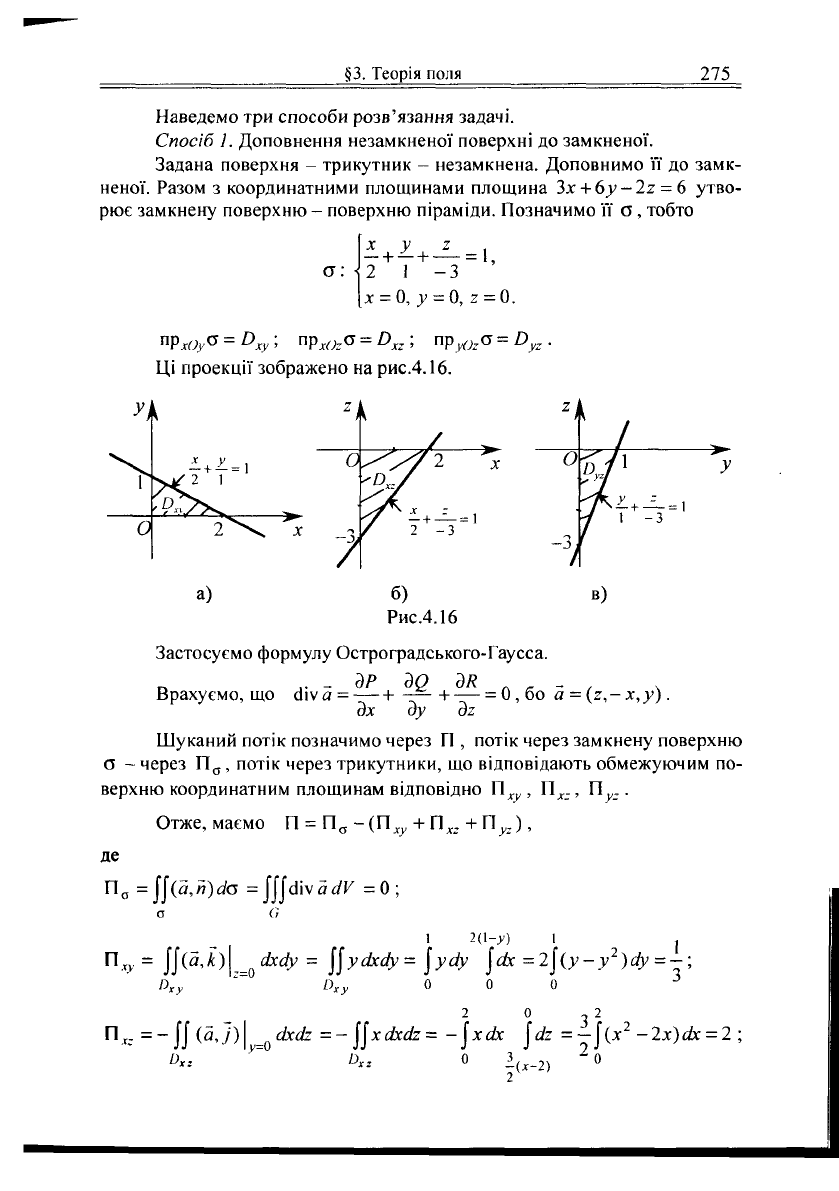
Ці проекції зображено

на

рис.4.16.

о/

і -з

в)

Застосуємо формулу Остроградського-Гаусса.

дР 8(3 а/с _ .

Врахуємо,

що

шV

а = 1- —— н = 0, бо а = (г, - х, у) .

дх

ду дг

Шуканий потік позначимо через

П ,

потік через замкнену поверхню

через

потік через трикутники,

що

відповідають обмежуючим

по-

верхню координатним площинам відповідно

ху

, П^.., П

Отже,

маємо

П = П

-(П + П„ +

П^,,),

де

=^(5,п)сіа

=\^д\\ас1У =0;

20-У)

П„

= Ц(а,к)\

<Ь<Іу

= \\ у

сіхау

= $

усіу

\(Ь =і\(у -

)ау

= -;

. - - Д

(5,7)|

сіхск

= -

її

хаха

"г

-^хсіх

^сіг = —^(x

-2х)сіх

= 2 ;

£>„ о з, ^ 0

|(*-2)

276

Глава 4. Криволінійні інтеграли. Поверхневі інтеграли. Теорія поля

у2

. -з о -з

(\ 3\ 23

Отже, П = 0- - + 2 + - =—-.

Спосіб 2. Застосування методу проектування на одну координатну

площину для знаходження потоку.

За умовою векторне поле а = гі

—

х} + ук ; поверхня о - трикутник,

отриманий від перетину площини Зх + 6у - 2і = 6 з координатними площи-

нами. Рівняння площини однозначно розв'язується відносно кожної з трьох

змінних, тобто існує взаємно однозначна відповідність між точками поверх-

ні і точками її проекції на будь-яку координатну площину.

Розв'яжемо це рівняння Зх + ву-2і = 6 відносно координати у :

Спроектуємо поверхню о на площину г = 0, а поверхневий інтег-

рал, що виражає потік, запишемо через подвійний інтеграл у вигляді

Оскільки нормаль до вибраної сторони поверхні утворює тупий кут з

віссю Ог , то соз у < 0 . Якщо функцію Р(х,у,г) представити у вигляді

то §гас! Р = Зі + 67 - 2к .

Тоді знаки соз у і Р'

=-2 співпадають і одиничний нормальний век-

у = —(Зх-2г-6).

Р(х,у,г)= Зх + 6у-2г-6 ,

тор п = +

2,гайР

§гасі ^|

де |егаа/

| =

л/9

+ 36 + 4 =7, п =-(ЗЇ + б]-2к), |й| = 1.

Звідси соз

= и„ = — .

Врахуємо, що а = (г,- х, у), тоді маємо

(а,п) 1

— = -(Зг-6х-2у).

созр 6

§3.

Теорія поля

277

Область інтегрування Б

ХІ

- проекція заданої площини на площину

хОг (рис.4.16 б), обмежена лініями Зх-22-6 = 0, х = 0, 2 = 0.

Отже,

П =І||

(32-6х-2у)\

у=

— \ах — г-5х-2

з/ ІЗ

і,, . „ахаї-

\у=--(іх-2:-6)

Й2 =

г<*-2)

Спосіб 3. Застосування методу проектування на кожну координатну

площину для знаходження потоку.

За умовою векторне поле а = іі - х} + ук ; поверхня о -трикутник,

отриманий від перетину площини Зх + 6у - 2г = 6 з координатними площи-

нами. Рівняння площини Зх + 6_у-2г =6 однозначно розв'язується віднос-

но кожної змінної, тобто маємо

„ „ 2 ,11 „ З

х = 2

—

2ул—г;

у = 1 Х +

—

2 = -ЗЧ—х + Зу.

3 2 3 2

Одиничний нормальний вектор п = ^

Отже, созооО,

созР>0,

созу<0.

Векторне поле а = (г,-х,у)

(див.

спосіб 2).

Запишемо у розгорнутому вигляді формулу для обчислення потоку,

враховуючи знаки напрямних косинусів нормалі

3 і Ч

П= + ^гаусіг +

||(-х)йх<&

- ^уахау^ ^гсіх ^сіу -^сіх ^сіг

й„.

їх. о

„ -зо о з, ,.

° |(-2)

211-у)

0 -з

2+- 02

+ |{(х

-2х)Л -

){у-у

)ау = ~.<

Приклад

9. Знайти потік радіуса-вектора г=х/ +уі+гк

через зовнішню сторону поверхні

а -

прямого кругового

цилінд-

ра,

якщо початок координат співпадає з центром нижньої

осно-

ви

циліндра, Я - радіус основи циліндра, Н - його висота.

• Поверхню а зображено на рис.4.17.

278

Глава 4, Криволінійні інтеграли. Поверхневі інтеграли. Теорія поля

І"-""'

То

'*\

Рис.4.17

Спосіб

Поверхня

замкнена, тому застосовуємо формулу Остро-

градського-Гаусса:

П = Дя)

сто"

= Д|аіу ^ ^ •

Маємо сііу

? = 3.

Отже,

П =

зДрК

тл

3 л/?

Спосіб

Врахуємо,

що на

бічній поверхні циліндра е>]

: (г,п) =

= пр

= Я ; на

верхній основі циліндра

Рп^ - Н ; на

нижній

основі циліндра

: =

пр^Я

= 0.

Тоді

= П, +П

+П

Д(?,Л)</0+ \\(г,п)а\5+ \\(г,п)ск>

= ///?ййт

+ Д//<Ат +

//0оЬ

Я-2пЯН

НпЯ

+ 0 =

ЗкЯ

.А

О)

СТ2 СТз

Обчислення циркуляції векторного поля

Приклад

10.

Обчислити циркуляцію векторного поля

а=уі+х

]-гк

по контуру

Ь:

\х

+у

\г

безпосередньо, використовуючи означення циркуляції,

за

формулою Стокса.

•

Контур

І -

коло радіуса

Я = 2, яке

лежить

на

площині

2 = 3.

Виберемо орієнтацію

на

колі таку,

як

вказано

на

рис.4.18.

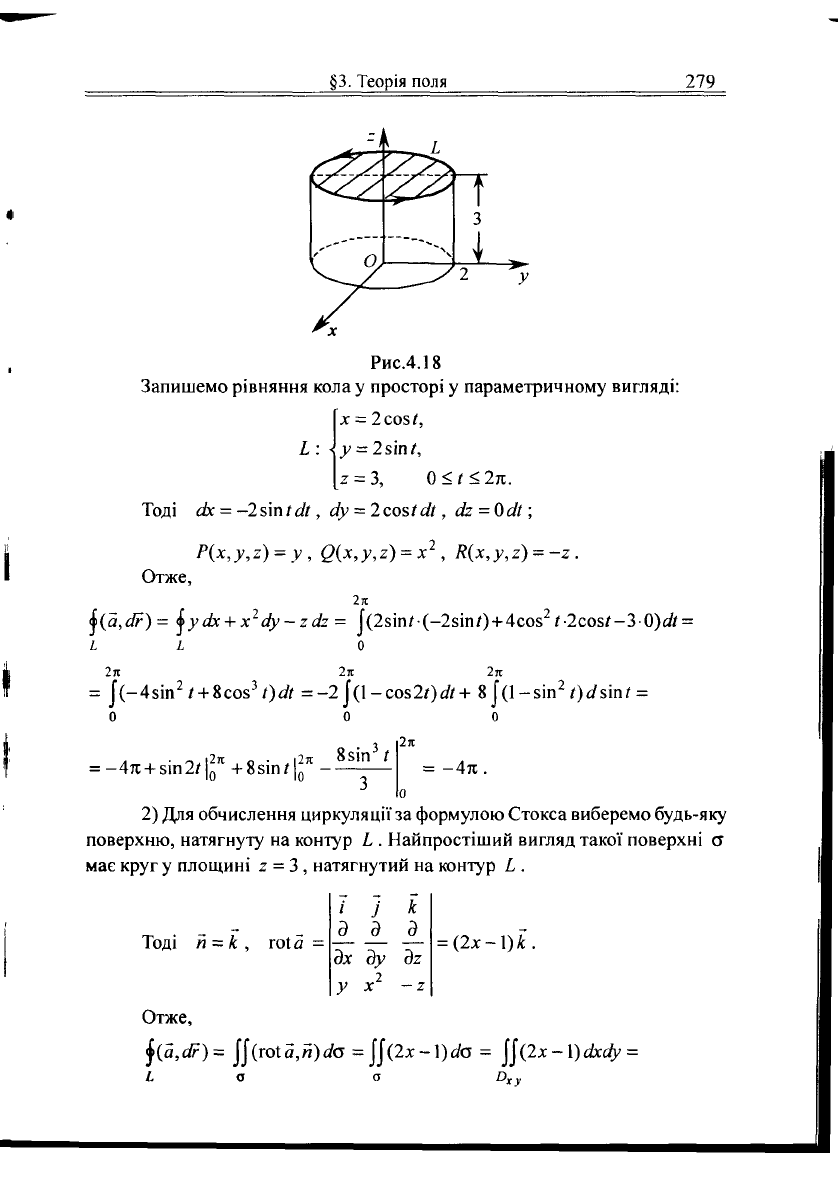
§3.

Теорія поля

279

Рис.4.18

Запишемо рівняння кола у просторі у параметричному вигляді:

х = 2

соз/,

Ь :

у = 2 зіп і,

[г = 3, 0<г<2л.

Тоді сіх = -2зіпгй?ґ

сіу =

2со5(сі(,

сіг =

Осії;

Р(х,у,г) = у ,

(2(х,у,г)

= х

, К(х,у,г) = -г.

Отже,

2л

§(а,сі?)= §ус1х + х

сіу-гсіг = |(25Іпґ(-2зіп/) + 4соз

/-2со5Г-30)^:

її

2л

2л 2л

= |(-45Іп

/ + 8соз

/)Л = -2 |(1-соз20<Л + 81(1 -зіп

/)і/5ІпГ

—

=-471 + 5іп2/|

+851П/|

2л

= -471 .

2) Для обчислення циркуля ції за формулою Стокса виберемо будь-яку

поверхню, натягнуту на контур і . Найпростіший вигляд такої поверхні а

має круг у площині 2 = 3, натягнутий на контур Ь .

Тоді Я = к , тоїа =

Отже,

] к

д_ д_ д_

дх ду дг

ух

-І

= (2х-Х)к .

$<а,сіг)=

_[[(гої.а,Я)йго-

=||(2х-1)йа = \$2х-$ сіхсіу =

280

Глава 4. Криволінійні інтеграли. Поверхневі інтеграли. Теорія поля

сіхау = рф<Лр, О':0<р<2, 0<ф<2тс.

2к

2 2к 2

= 2||р

созффйф- ||рф<Лр = 2|созфйф|р

ф - |<іф|рф =

О' /У 0 0 0 0

Приклад

11. Обчислити циркуляцію С векторного поля

= хуі + уг}

хгк вздовж кривої Ь:

дг

= соз/, у = зіп/,

= 1-

соз

і - зіп і у

напрямку зростання параметра

І (0 < і <

2 л):

безпосередньо,

використовуючи

означення циркуляції,

за формулою Стокса.

•

1) Обчислюємо циркуляцію С безпосередньо:

Знайдемо сіх

=-5ІПІСІІ,

сіу = со5Ісіі, сіг = (зіпІ-созі)сії.

Тоді

ху

сіх + уг сіу + хг сіг =

= (-8ІП

ГСОЗ/

5ІПГ(1

—

СОЗ?-5ІП/)С05/

С05і(\-СО$1

ЗІП/)(зІП/-С05і))сІІ

С =

(а,

сіг)

= у ху

+ уг ау +

хг

<І2

= (-3 зіп

СОЗ

/ + 2 зіп

соз і - зіп

соз

1 - соз

/ + соз

/) сії.

Маємо

С = і(-3зіп

?созг + зіп2і-зіп/соз

/-соз

1 + соз

1)сії =

І.

0 0 0

2к

= -зіп і—соз2г +

СОЗ

І 1

~~3 2

8ІП2/ +

5ІПГ-

2 4

)

-71 .