Тевяшев А.Д., Литвин О.Г., Кривошеєва Г.М. та ін. Вища математика у прикладах та задачах. Ч 2

Подождите немного. Документ загружается.

§2.

Поверхневі інтеграли

241

Обчислення поверхневого інтеграла другого роду

Обчислення поверхневого інтеграла другого роду зводиться до обчи-

слення поверхневого інтеграла першого роду, а отже до обчислення подвій-

ного інтеграла.

Якщо поверхня о однозначно проектується на площини хОу, уОг ,

хОг, то мають місце формули відповідно для кожної із площин:

Ах.Ау, , Ау.Аг, , Ах.Аг.

Ао,=-^г, Ао,=-^-, Ас,=-^г, (4.34)

С05У

|С05СХ|

С05(3

які можна використати для обчислення поверхневого інтеграла другого роду.

Метод проектування на всі три координатні площини.

Нехай поверхня о однозначно проектується на всі три координатні

площини. Тоді рівняння Ф(х,у,г) = 0 поверхні а однозначно розв'язуєть-

ся відносно кожного з аргументів х, у , і так, що

х = х(у, г), у = у(х, г), г =

г(х,у).

(4.35)

Позначимо пр

Юу

а = О

ху

, пр

х0

,а = О

,, пр^,ст = Б

у2

. Підставимо

формули (4.34) і (4.35) у формулу (4.33).

Отримаємо формулу для обчислення поверхневого інтеграла другого роду:

Я(Рсоза

£?со8[}+/?созу)до

= ± ^Р(х(у,г),у,г)ауаг±

а і)

ЦО(х,у(х,г),г)сіхсіг

\\К(х,у,г(х,у))ахОу

. (4.36)

х:

ху

Знак в кожному із доданків правої частини формули (4.36) вибираєть-

ся таким, який знак мають созсх, созр, созу на орієнтовній поверхні а.

Метод проектування на одну із координатних площин.

Якщо незамкнена поверхня ст однозначно проектується на площину

хОу в область Б

ху

, а рівняння поверхні можна задати рівнянням г = г(х,у)

Ах.Ау.

і за формулами (4.34) Лст, = - -, то поверхневий жтефап другого роду

созу |

перетворюється на подвійний інтеграл по області Б

ху

созу

сіхау.

(4.37)

242

Глава

Криволінійні інтеграли. Поверхневі інтеграли. Теорія поля

Якщо поверхня

однозначно проектується

на

площини

хОг або

уОг

, то

поверхневий інтеграл другого роду перетворюється

на

подвійний

за формулами:

Я(7?,Я)Л=

С08р|

|со8а|

ауск.

(4.38)

(4.39)

Зауважимо,

що

коли поверхня

кусково-гладка, тоді

її

розбивають

на гладкі поверхні,

які

однозначно проектуються

на

координатні площини,

далі обчислення проводять

по

кожній окремій частині,

інтеграл

по

усій

поверхні

дорівнює сумі інтегралів

по

усім частинам.

Формула Остроградського-Гаусса

Формула Остроградського-Гаусса встановлює зв'язок

між

поверхне-

вим інтегралом другого роду

по

замкненій поверхні

по

зовнішній

її

стороні

і потрійним інтегралом

по

області

О,

обмеженій цією поверхнею.

Якщо поверхня

ст

замкнена,

функції Р(х,у,г),

<2(х,у,г),

К(х,у,г)

неперервні разом

із

своїми частинними похідними першого порядку

області

О,

обмеженій цією поверхнею,

то має

місце формула Остроградського-Гаусса:

Р(х, у, г)

ауаг

+ 0(х, у, г)

дхсЬ

+ К(х, у, г)

ахау

дх

ду дг

ахауаг. (4.40)

цій

формулі зліва інтегрування ведеться

по

зовнішній стороні поверхні.

Формула Стокса

Формула Стокса встановлює зв'язок

між

поверхневим

криволіній-

ним інтегралами.

Якщо функції Р(х,у,г), ()(х,у,г), Р(х,у,г) неперервні разом

із

свої-

ми частинними похідними першого порядку

на

кусково-гладкій поверхні

а,

яка обмежена кусково-гладкою замкненою кривою

Ь,

причому орієнтація кри-

вої

узгоджена

із

орієнтацією поверхні

а, то має

місце формула Стокса:

$Рах

+ ()ау + Ка2 =

дх ду

л. і дР ае

ахау

+ \-—

ду

Оуа'г

(дР_

дг

дК

дх

ОхОг

(4.41)

§2.

Поверхневі інтеграли

243

Зазначимо, що орієнтація кривої Ь, обмежуючої поверхню о, вважа-

ється узгодженою із орієнтацією цієї поверхні (орієнтація поверхні а зада-

ється напрямом нормалі п до неї), якщо спостерігач, який дивиться з кінця

нормалі Я, бачить обхід вздовж кривої і проти годинникової стрілки.

Зауваження. Якщо поверхня а лежить на площині хОу , то формула

Стокса (4.41) переходить у формулу Гріна, тобто

Застосування поверхневого інтеграла другого роду

Якщо вектор-функція Р(х,у,г) = у(х,у,г) є швидкість руху рідини,

яка протікає через поверхню о в сторону, визначену напрямком вектора

нормалі п, то кількість рідини П , що протікає через цю поверхню в одини-

цю часу, обчислюється за формулою:

П = ||(у,й)^о. (4.42)

//. Контрольні питання та завдання

Що називається поверхневим інтегралом першого роду?

Як обчислюється поверхневий інтеграл першого роду?

Які застосування має поверхневий інтеграл першого роду?

Як знайти масу матеріальної поверхні за допомогою

поверхневого інтеграла першого роду?

Які поверхні називаються двосторонніми? Наведіть прикла-

ди двосторонніх поверхонь.

6. Яку поверхню називають орієнтовною?

Що називається поверхневим інтегралом другого роду?

8. Як обчислюється поверхневий інтеграл другого роду?

9. У чому полягає різниця між поверхневими інтегралами

першого і другого роду?

10.

У чому полягає зв'язок між поверхневими інтегралами

першого і другого роду?

11.

Наведіть формулу Остроградського-Гаусса.

244 Глава 4, Криволінійні інтеграли. Поверхневі інтеграли. Теорія поля

12.

Наведіть формулу Стокса.

13.

Яке застосування має поверхневий інтеграл другого роду?

///. Приклади розв'язання задач

Поверхневі інтеграли першого роду

Приклад 1. Обчислити поверхневий інтеграл першого роду

>х

+ 4у + Зг)

сі<У,

де а - частина площини х + 2у + Зг = 6,

Поверхню о та її проекцію й

ху

на площину хОу зображено на

рис.4.5,

де й - трикутник: 0 < ^ < 3, 0 < х <6-2у .

розташованої у першому октанті.

• Будемо використовувати формулу (4.27):

Ц Ах, у, г) сів = Ц /(х, у, г(х,

у)),}\

+ г'

(х, у) + г'

(х, у) сЬсоу.

о О

ху

а)

Рис.4.5

Рівняння поверхні о : х + 2у + Зг = 6. Тоді

б)

2 =

1(6-2;/-*),

'х=-^

Отже,

^(6х + 4у + Зг)сІо =

О,

\\\бх + 4у +

3-(6-2у-х)

У1 +

§2,

Поверхневі інтеграли

245

)){5х + 2у + Є)ахау = -—\ау ](5х + 2у + 6)ах =

М —х +2ху + 6х

^ 0\^

л/Й

6-2 у

ау =

}^|(б - 2>>)

+ 2у(6 - 2>0 + 6 (6 - 2>0 ^ =

Щ-\$У

-60у

+ \26)сіу=~ (2/ -ЗОу

+126>>)[ =

л/Ї4

162 = 54л/Ї4

Приклад 2. Обчислити поверхневий інтеграл першого роду

||^1 + 4х

4у

сіо, де а - частина поверхні параболоїда

= 1- х

->'

, яка відтинається площиною 2 = 0.

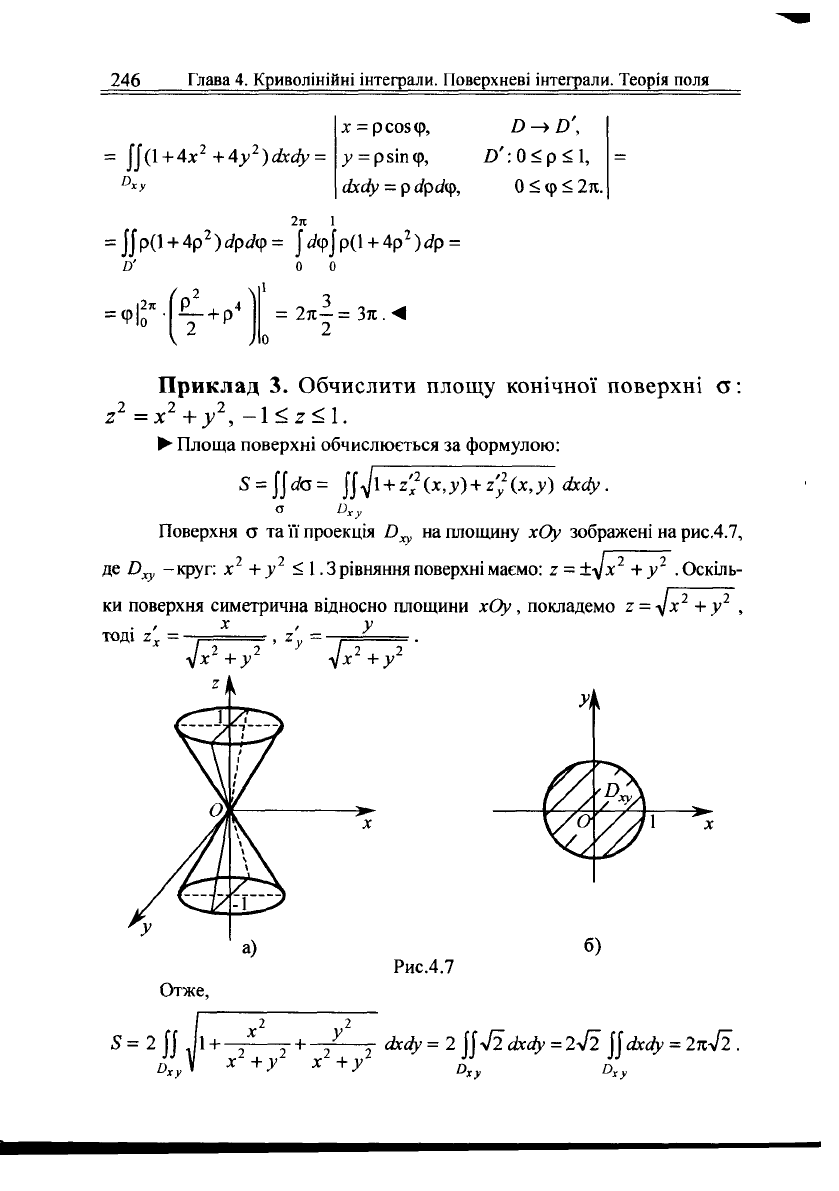
• Поверхню о~ та її проекцію й

ху

на площину хСТу зображено на

рис.4.6,

де й

ху

- круг х

+ у

<1. Рівняння обмежуючого кола отримаємо,

якщо в рівнянні поверхні а покладемо 2 = 0.

Рис.4.6

Маємо: г'

= -2х, г'

= —2у .

Отже, за формулою (4.27):

Д>/і + 4х

+ 4у

ііа= \\у1і + 4х

+ 4у

^1 + (-2х)

+(-2у)

ахау =

246

Глава

Криволінійні інтеграли. Поверхневі інтеграли. Теорія поля

+ 4х

+4у

)ахау

рС05ф,

—>

Б',

рзіпф,

£)': 0 < р < 1,

сіхсіу

= р

фаф,

0 < ф < 2тс.

2л

= Д

(1 +

4р

)ф^ф= |йф|

4р

)ф:

О'

0 0

= ФІо"-

2я-=

Зя.-4

Приклад

Обчислити площу конічної поверхні

а:

+у

-1<2<1.

• Площа поверхні обчислюється

за

формулою:

= Я*

Я^

1 +

?(*>3')

?(*»>)

<&Ф-

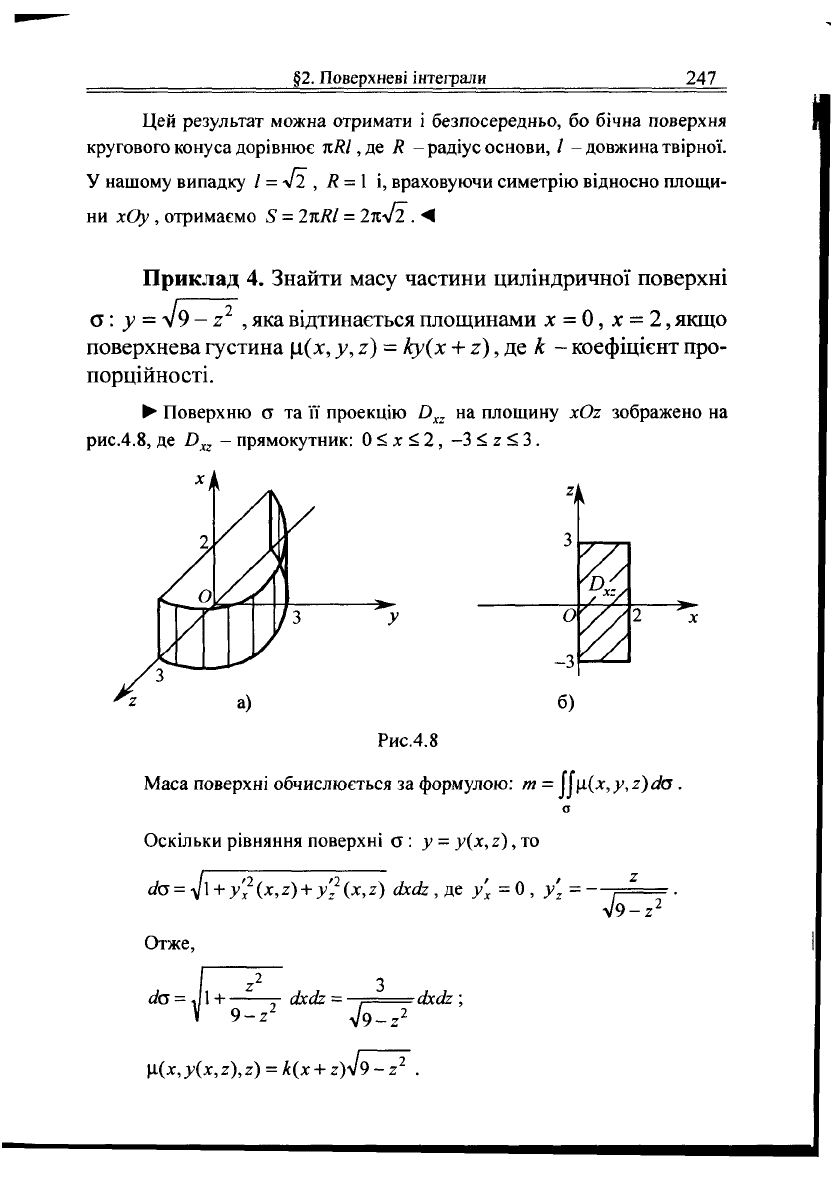
Поверхня

ст та її

проекція

Б^ на

площину

хОу

зображені

на

рис.4.7,

де

ху

круг:

+ у-

< 1.3

рівняння поверхні маємо:

г =

±-у/*

+ у

. Оскіль-

ки поверхня симетрична відносно площини

хОу,

покладемо

г = -^х

+ у

тоді

г'

б)

Рис.4.7

Отже,

5=2

Я,

-2

-Т

2 2 2

аха>

= 2 Я^2

сіхсіу

2л/2 Я<&Ф

2я>/2

§2,

Поверхневі інтеграли

247

Цей результат можна отримати і безпосередньо, бо бічна поверхня

кругового конуса дорівнює л/?/,де Я -радіус основи, / - довжина твірної.

У нашому випадку / = 4і , К = 1 і, враховуючи симетрію відносно площи-

ни хОу, отримаємо 5 = 2кКІ =

Приклад

4. Знайти масу частини циліндричної поверхні

а:

у =

УІ9

- г

яка

відтинається

площинами х = 0, х = 2, якщо

поверхнева

густина |і(х, у, г) = ку(х + г),дє к - коефіцієнт

про-

порційності.

•

Поверхню а та її проекцію О

ХІ

на площину хОг зображено на

рис.4.8,

де й

хг

- прямокутник: 0 < х < 2, -3 < 2 2 3.

'і

-3

2 *х

б)

Рис.4.8

Маса поверхні обчислюється за формулою: т =

]]\і(х,у,г)Ау

Оскільки рівняння поверхні а: у =

у(х,г),

то

СІО

у1\+у'

(X,

2) +

у'} (X,

СІХск,ДЄ

Ух

= 0, /

=•

49-7

Отже,

*йт

,|ін

г- ахаг = -7= ахск ;

9-2

7о^7

ц(х,у(х,2),2)

= Ж(х +

г)л/9-2

248

Глава 4. Криволінійні інтеграли. Поверхневі інтеграли. Теорія поля

Тоді

т= і

]ку(х + 2)с/о = ]]к(х +

г)49-2

—=2===сЬсск =

= 3к \\(х + 2)скск= Зк\ск\(х + 2)ах = Зк|

-з

• +

Х2

ск-

= Зк\(2 + І2)ск= 6*2

—

-2

-з

= 36к.<

Поверхневі інтеграли другого роду

Приклад

Обчислити поверхневий інтеграл другого

роду

Д х

сіусіг +

сксіг •+

сіхсіу,

де о - верхня сторона частини пло-

щини

х +

-1 = 0, яка лежить у першому октанті і відтинаєть-

ся

площинами у = 0 і у = 4.

•

Поверхня а зображена нарис.4.9. Оскільки розглядається її верх-

ня сторона, то вектор нормалі п утворює гострий кут з віссю Ог .

Рис.4.9

Будемо використовувати метод проектування на всі координатні пло-

щини за формулою (4.36).

- прямокутник: 0<>><4, 0 < 2 < 1;

ху

- прямокутник: 0< у<4, 0 < х < 1 ;

Х7

- пуста множина, тому що площина х + г -1 = 0 перпендикуляр-

на площині хОг.

Маємо г(х, у) =

- х , х(у, г) =

- 2 .

§2.

Поверхневі інтеграли

249

Отже,

|| х ауск + у йхск +1 йхау = ]]х(у,2)ауаг + ]]у(х,г)ахск +

4 1

+ \\г(х,у)ахау=

\\(\-2)ауск+

\\(\-х)ахау = \сіу\(\-х)ах +

4 1

4 ]

'ху

+ \ау\(\-г)а2= 2]ау\(\-х)ск=2\

0 0 0 о

—

- ау=2^ау = 4.

Оскільки нормальний вектор п утворює із осями Ох і Ох гострі кути,

то у формулі (4.36) вибрали знак "+" в кожному доданку. Л

Приклад 6. Обчислити поверхневий інтеграл другого роду

||(*

+ у

)сіхсІ2,де

о -зовнішня сторона конічної поверхні

ліх

+ г

, яка відтинається площинами у = 0, у-Ь, Ь>0.

• Поверхня о та її проекція £>

. на площину Охг зображені на

рис.4.10, де й

. - круг: х

+г

<Ь

а) б)

Рис.4.10

Будемо використовувати метод проектування на координатну площи-

ну за формулою (4.36). Нормаль « до поверхні ст утворює з віссю Оу ту-

пий кут, тобто

С05р"

< 0.

Отже,

\\(х

+у

)ахсЬ= - || ^х

+ (V*

+ 2

| + г

^ахск

250

Глава 4. Криволінійні інтеграли. Поверхневі інтеграли. Теорія поля

= -2 Д(л:

)скаг

Ох,

х = рсозф,

І2

-*О

у,

2 = р8іпф, £>

рф

: 0 < р < 6,

сЬсаг

= р

ф<Лр,

0 < ф < 2я.

2л

-2

Др

ф<Ар

- 21

йЛр/р

ф = -

•

2я*

о о

Приклад 7. Обчислити поверхневий інтеграл другого роду

Д х

аусіг

ахсіг

сіхау,

де о - зовнішня сторона поверхні ефе-

сі

ри х

+ у

яка розміщена у другому октанті

(д:

< 0, у > 0,

2>0).

•

Поверхня а та її проекції на координатні площини зображені на

рис.4.11 та рис.4.12. Проекції й^, й

Х2

, є чверті кругів з центром у

початку координат і радіусів рівних одиниці. Одиничний вектор нормалі п

до поверхні о утворює гострі кути з осями Оу і

От.

і тупий кут з віссю Ох,

тому соза<0, созР>0, созу>0.

Рис.4.11