Тевяшев А.Д., Литвин О.Г., Кривошеєва Г.М. та ін. Вища математика у прикладах та задачах. Ч 2

Подождите немного. Документ загружается.

§1.

Криволінійні інтеграли

231

4.9. |(х

+ у

)" сії, де Ь - коло х = асові, у = авіпі.

4.10. |

д/^У

сії

,де Ь - перша арка циклоїди

х = а(і-віт), у = а(\-сові), 0<і<2п.

4.11.

](х~у)сі1, де X - коло х

= ах (перейти до

полярних координат).

4.12.

|х-^х

- у

сії,де І -лемніскатаБернуллі (х

+ у

)

= а

(х

- у

) (х > 0) (перейти до полярних координат).

4.13.

|(х

+ у

)сії, де Х - дуга логарифмічної спіралі

р = ае

3ф

від точки А(а,0) до точки 0(0,0) .

г У • •

4.14.

агсІ§,—сії,

де Ь - частина спіралі Архшеда р = 2ф,

І *

яка лежить всередині кола радіуса К з центром у початку коор-

динат (у полюсі).

. . _

СІІ

„

4.15. —г -, де Ь - перший виток гвинтової лінії

І* +У

х = асові, у = авіпі, 2 = аі, 0 < і < 2п .

4.16. ] хуг сії, де І - чверть кола, утвореного перетином

Т О О 9 "7 9

сфери х + і> +2 =7? і циліндра х + у = —, що лежить в

першому октанті.

. „ г У<Я т • ...

{1 (і

•

4.17. — , де Ь - дуга лінії х = /, у =

-і=,

2 = — від

{х + Зг л/2 З

' 2>/2

точки 0(0,0,0) до точки 5

л/2, л/2,

232 Глава 4. Криволінійні інтеграли. Поверхневі інтеграли. Теорія поля

У задачах 4.18-4.21 обчислити довжину кривої Ь за до-

помогою криволінійного інтеграла першого роду.

4.18. Ь - ланцюгова лінія у = спх, 0 < х < 1.

4.19. Ь - крива, задана рівнянням х = 2 , у = —, що

4 6

обмежена точками перетину її з осями координат.

4.20. Ь - гвинтова лінія х = 4а соз /, у = 4а зіп І, г = Заі,

0 < і < 2ті.

4.21.

Ь - дуга конічної гвинтової лінії х =

ае'соз(,

у = ае' зіп і, і = ае

від точки О(0,0,0) до точки Л(а, 0, а).

У задачах 4.22 - 4.26 знайти масу матеріальної дуги 1,

якщо задана густина |і(х, у).

4.22.

Ь - дуга кривої у = \пх між точками з абсцисами

д:,

А/з

та х

= >/8, густина кривої в кожній точці дорівнює

квадрату абсциси цієї точки.

4.23.

Ь - ланцюгова лінія у

—

а спах між точками з абсциса-

ми х, = 0 та х

= а, густина в кожній точці обернено пропорцій-

на ординаті точки, причому в точці

(0,

а) густина дорівнює 5.

424.1

чверть

еліпса —

що лежить в першому квад-

ранті, густина в кожній точці дорівнює добутку координат цієї точки.

4.25. Ь - лемніската Бернуллі р

=а

со§2ф, густина

М-(х,

у)~кр, к ~ коефіцієнт пропорційності, к > 0.

4.26. Ь:х = аі ,у = ^і

, г = у/

, 0<(<\, густина

Криволінійні інтеграли

233

Криволінійні інтеграли другого роду

У задачах 4.27 - 4.40 обчислити криволінійні інтеграли

другого роду.

4.27. |(х

)сіх,

де І - дуга параболи у = х

від точ-

ки 0(0,0) до точки А(2,4).

4.28. | ху

сіх

+ (у - х) сіу, де Ь

у = X

від точки О(0,0) до

точки Д1,1).

4.29. ](у + х

)сіх+ (2х - у)сіу, де Ь - дуга параболи

у = 2х-х

від точки ДІД) до точки 5(3,-3).

4.30.

[

х сіу, де Ь - відрізок прямої

—

від точки

а Ь

перетину її з віссю абсцис до точки перетину її з віссю ординат.

4.31.

| - х соз у

сіх

+ у зіп х сіу, де Ь - відрізок прямої від

точки 0(0,0) до точки А(к,2к).

4.32.

| х сіу, де Ь - контур трикутника, утвореного осями

У і • /-

координат і прямою

—

+ у = 1, у додатному напрямі (проти го-

динникової стрілки).

4.33.

](х

)сіу,

де Ь - контур чотирикутника з вер-

шинами (вказаними в порядку обходу) в точках ДО, 0), 5(2,0),

С(4,4) і ДО, 4).

4.34. ]усіх + хс1у, де Ь - чверть кола х = Лсоз/,

у = К зіп/ від /, =0 до 1

= —.

234

Глава

4. Криволінійні інтеграли. Поверхневі інтеграли. Теорія поля

4.35. І усіх- х сіу, де Ь - еліпс х = а соз/, у = бзіп І, що

пробігається в додатному напрямі.

4.36. ^ (2а - у)

сіх

+ х

сіу

, де Ь - арка циклоїди

х = а (/ - зіп/), у = а

- соз/), 0 < / < 2к.

. -.т г(х + У)сІХ-(х-у)сІу

Т 2

2 2

4.37. р —Ч—^-^-,де І - коло х

+ у =а

І * +У

при обході проти годинникової стрілки.

„_

г хсіх + усіу

. х

4.38.

—==============,

де І - чверть еліпса — + Аг- = 1, яка

лежить у першому квадранті, здійснюючи обхід за годиннико-

вою стрілкою.

4.39. |

хсіх

+ усіу + (х + у -1) сіг, де І - відрізок прямої від

точки (1,1,1) до точки (2,3,4).

4.40. | уг

сіх

+ г^К

- у

сіу

+ ху сіг, де Ь - дуга гвинтової

. ... „ . аі . ...

лінії х = я соз /, ^ = л зіп /, 2 = — від точки перетину ЛІНИ з

2л

площиною г = 0 до точки її перетину з площиною г = а .

У задачах 4.41 - 4.46 обчислити криволінійні інтеграли

другого роду по замкненим додатно орієнтованим контурам Ь

безпосередньо і за формулою Гріна.

4.41.

| (х + у)

сіх

- 2хсіу, де І - контур трикутника зі сто-

ронами х = 0, у = 0, х + у = а.

4.42.

|—сіх

— —

сіу, де Ь - контур трикутника з вершина-

ЇУ

ми ДІД), 5(2,1) і С(2,2).

2 2 2

4.43.

Ф2(х +>> )б&г +

(х-г->')

с/у,де X - контур трикут-

ника з вершинами Д1,1), 5(2,2), С(1,3).

§1.

Криволінійні інтеграли

235

4.44. §ху

сіу

усіх,

де Ь -

коло

4.45. §(\-х

)усіх +

х(\

+ у

)сіу,де

-коло

4.46.

| (ху

у)

сіх

(ху

х- у)

сіу

де

Ь: а)

еліпс

^-т-

-^г-

= 1; б)

коло

ах .

У задачах 4.47

4.53 перевірити,

що під

знаком криволі-

нійного інтеграла стоїть повний диференціал,

та

обчислити цей

криволінійний інтеграл.

(2,3)

4.47.

| у

ах +

сіу

(-1,2)

(2,1)

4.48. 12ху

сіх

+ х

сіу.

(0,0)

*ІХ

'г

хсіх + усіу

4.49.

—г —

(початок координат не лежить на кри-

4) X

вій інтегрування).

(3.

4.50.

\(х

+4ху

)сіх + (6х

-5у

)сіу.

(-2,

-1)

(2,

4.51.

](х

у)сіх+

(х -

у)сіу.

(0,

(2,1,3)

4.52.

сіх

сіу

+ 2

сіг

(1,-1,2)

(3,2,1)

4.53.

| уг

сіх +

хг

сіу

ху

сіг.

(1,2,3)

236

Глава 4. Криволінійні інтеграли. Поверхневі інтеграли. Теорія поля

У задачах 4.54 - 4.60 знайти функцію за заданим повним

диференціалом.

4.54. сій = х

сіх +

сіу.

4.55.

сій

= 4(х

- у

) (хсіх - усіу).

4.56.^

(

+ 2

^ + ^.

(х + у)

4.57.

сій

= (2х соз у - у

зіп х)

сіх

+ (2у соз х - х

зіп у) сіу.

4.58.

^=>

X + у + 2

4.59.

сій = (х

- 2уг)

сіх

+ (у

- 2хг)

сіу

+ (г

- 2ху)

сіг

хсіх + усіу + гсіг

4.60. сій =

У задачах 4.61 - 4.67 обчислити площу фігур, обмежених

заданими замкненими кривими Ь за допомогою криволінійно-

го інтеграла другого роду.

4.61.

І - еліпс

4.62.

Ь - арка циклоїди

х = а соз/,

[у = Ь$'ті, 0</<2л.

х = а (І - зіп (),

[у = а(\ -соз/), 0</<2я.

4.63.

Ь - астроїда

х = а соз /,

[у = азіп

/, 0</<2тс.

4.64. Ь -листДекарта

х =

За/

1 + /

ЗаГ . ^ ^ тс

= 0</<-.

1 + /

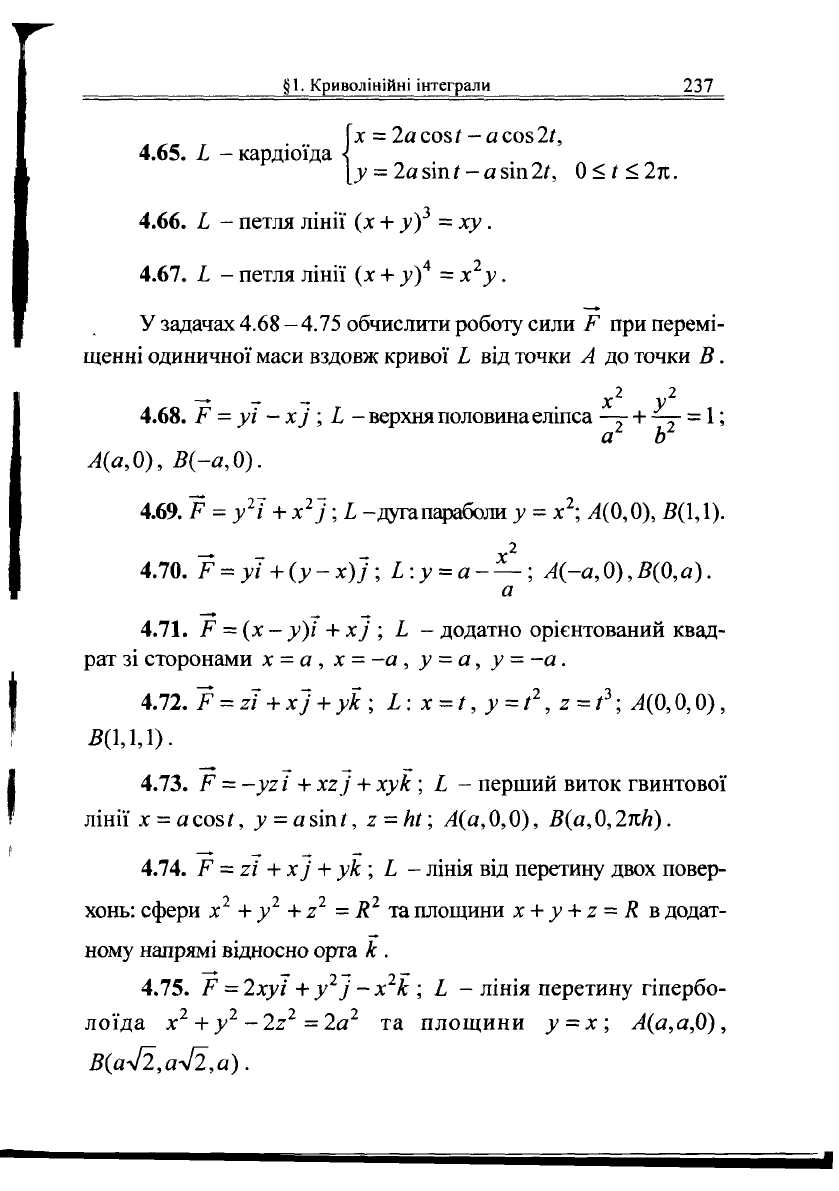
§1,

Криволінійні інтеграли

237

х = 2а соз/ -а соз

2/,

у = 2а зіп / - а зіп

21,

0 < / < 2л.

4.66. І - петля лінії (х + у)

= ху.

4.67. Ь - петля лінії (х + у)

= х

у.

У задачах 4.68 - 4.75 обчислити роботу сили Р при перемі-

щенні одиничної маси вздовж кривої Ь від точки А до точки В.

2 2

4.68. Р = уі - х^ ; І - верхня половина еліпса — + ^у"

Л(в,0),

5(-я,0).

4.69. Р = у

і + х

] ; Ь -дугапараболи у = х

; А(0,0), 5(1,1).

- - х

4.70. ^ = я

+(^-х)У

; Ь:у = а ; А(-а,0),В(0,а).

4.71.

Р = (х

—

у)і + х/ ; І - додатно орієнтований квад-

рат зі сторонами х = а , х = -а ,

_у

= а, у = -а.

4.72.

Р = гї + х]

ук; Ь: х = ґ, у = І

, г = I

; ДО, 0,0),

5(1,1,1).

4.73.

Р = -уг і + хгі + х_у£; £ - перший виток гвинтової

лінії х = а соз /, ^ = а зіп/, г = Ні; А(а, 0,0), 5(а,0,2тг7г).

4.74. Р = гі + хі + ук ; Ь - лінія від перетину двох повер-

хонь:

сфери х

+ .у

+ г

= і?

та площини х + у + г = К в додат-

ному напрямі відносно орта к .

4.75. Р = 2хуі + _у

у - х

к; Ь - лінія перетину гіпербо-

лоїда х

+ у

-2г

=2а

та площини у = х; А(а,а,0),

В(а^2,алІ2,а).

Глава

Криво.т

Г.

Поверхневі інтеграли. Теорія поля

/4ні відомості

неві інтеграли першого роду

.гтя.

Поверхня називається гладкою, якщо в кожній її

а площина і при переході від точки до точки положення

лцини змінюється неперервно. Поверхня, яка складається

числа неперервно сполучених гладких поверхонь, називаєть-

ся ку. .адкою.

Не^ай в точках деякої кусково-гладкої поверхні а визначена неперервна

функція /(х, у, г). Розіб'ємо поверхню а на п частинних поверхонь а, без

спільних внутрішніх точок. Позначимо площу кожної із них Ла,. Покладемо

X = тах сі,, і = 1, п, де а", - діаметр /' -ї частинної поверхні. На кожній частин-

ній поверхні о~, візьмемо довільну точку М,(і%,,г\,, £,) і складемо суму

=ІДМ,)Да,.

Ця сума називається інтегральною сумою для функції Дх, у,і) по

поверхні а.

Означення. Якщо існує границя Ііт ^/(М,)Аа,, яка не залежить

від способу розбиття поверхні о та від вибору точок М,, то ця границя

називається поверхневим інтегралом першого роду від функції / (х, у, г) по

поверхні о.

Позначення: ]]/(х,у,г)сіа.

Отже, за означенням

\\Дх,у,г)сі<5 = 1ітДлМ,)Да,. (4.26)

і=і

0§ч\«.5дач\га

штрхиевого інтеграла першого роду

Обчислення поверхневого інтеграла першого роду зводиться до об-

числення подвійного інтеграла.

Нехай поверхня а задана рівнянням г = г(х,у) і будь-яка пряма, па-

ралельна осі Ог, перетинає цю поверхню лише в однієї точці, тобто поверхня

а однозначно проектується на площину хОу . Проекцією поверхні а на

§2.

Поверхневі інтеграли

239

площину

хОу є

область

О ,

тобто

пр

Юу

= й

ху

Функція

г(х,у)

непере-

рвна

із

своїми частинними похідними першого порядку

в цій

області. Тоді

має місце формула:

ЦДх,у,

)сІа

ДДде,у,*<х,уУ^І

г'

(х,у)

сіхау.

(4.27)

ху

Аналогічно, якщо поверхня

задана рівнянням

у=у(х,і) і

пр

л0

.ст

= О

маємо:

ЦДх,у,

)сіС

ЦДх,у(х,2\

)7і

у?(х,г)

у'

(х,г)

сіхсії.

(4.28)

Якщо поверхня

задана рівнянням

х(у,г) і

пр

уП

.а=

О^.,

маємо:

\ІДх,у,і)сі<3

Ц/(х(у,

і\у,г)]\

х'

(у,г)

х'

(у,

г) сіуск

(4.29)

Застосування поверхневого інтеграла першого роду

а)

площа поверхні

обчислюється

за

формулою

5=|/<Лт. (4.30)

б)

маса

матеріальної

поверхні

а, в

кожній точці якої задана густина

\і.(х,у,г), обчислюється

за

формулою

Ціі(х,у,г)сіа

(4.31)

Поверхневі інтеграли другого роду

Основні поняття. Гладка поверхня

називається

двосторонньою,

якщо

обхід

по

будь-якому замкненому контуру,

що

лежить

на

поверхні

ст і не має

загальних точок

з її

межею,

не

змінює напрямку нормалі

до

поверхні. Якщо

на поверхні існує замкнений контур,

при

обході

по

якому напрямок нормалі

змінюється

на

протилежний,

то

поверхня називається

односторонньою.

Двосторонню поверхню називають

орієнтовною,

вибір певної

сторони

поверхні, тобто вибір напрямку нормалі

до

поверхні, називається

орієнтацією

поверхні.

Нехай задана кусково-гладка орієнтовна поверхня, сторона якої зада-

сться нормальним вектором

п:

п =

со50і/

+созру

созуЛ

ле

соза,

созр\

соз у -

напрямні косинуси вектора

п,

п\ = 1.

240

Глава

Криволінійні інтеграли. Поверхневі інтеграли. Теорія поля

Крім того,

на

поверхні

задана вектор-функція Р(х,у,г):

Р(х,

у,

Р{х,

у,

2)7

+ у, 2)і

+ К{х,

у,

2)ї

де Р{х,у,г),

(3(х,у,2),

К(х,у,г)

неперервні функції.

Розіб'ємо поверхню

о на

частинні поверхні

а,, і = 1, п ,

площі яких

позначимо

Аа,

.Покладемо

X = шах сі,, і = \, л,де сі, -

діаметр

і -ї

частин-

ної поверхні. Візьмемо довільну точку М,(^,,ті,,

£,)є о,,

обчислимо

Р(М,)

і Я(Л/

(

)

= п, і

складемо суму

=І(?(М,),/7(М,))Аст,

= ^[Р(М,)соза,

+Є(Л/,)со5р, +/г(Л/,)со$у,]Аст,.

(4.32)

і=і

Ця сума називається інтегральною сумою від вектор-функції

Р(х, у, г)

по стороні поверхні

а,

визначеної нормальним вектором

п.

Означення. Якщо існує границя

Ііт /„ , яка не

залежить

від

способу

Х.-»0

розбиття поверхні

о та від

вибору точок

М,, то ця

границя називається

поверхневим інтегралом другого роду

від

вектор-функції

Р(х, у, г) по

сто-

роні поверхні

о,

визначеної нормальним вектором

п.

Позначення:

]](Р,п)сЬ;

Д(,Рсо5а

£со5Р

/ссозу)</а;

Драусіг

+ ()ахаг + Кахау

ста

Отже,

за

означенням

або

||(Р соз

а +

соз

+ К

созу)

сів =