Тевяшев А.Д., Литвин О.Г., Кривошеєва Г.М. та ін. Вища математика у прикладах та задачах. Ч 2

Подождите немного. Документ загружается.

Глава 3, Кратні інтеграли

191

Координати центра ваги пластинки обчислюються за формулами:

=~,

Ус= —

т т

де т - маса пластинки,

,М

-її статичні моменти відносно координат-

них осей.

У випадку однорідної пластинки ці формули приймають вигляд:

Цхііхсіу Цусіхсіу

С г. ' Ус СІ '

де 5 - площа області О .

Моменти інерції пластинки О відносно осей Ох і Оу знаходяться

за формулами:

їх = ЦУ

^(х,у) сіхау, І

= Цх

[і(х, у) сіхсіу ,

а момент інерції відносно початку координат - за формулою:

'о =Ц(х

+у

)\і(х,у)сіхсіу =

+І

Застосування потрійного інтеграла

Обчислення об'єму тіла

Об'єм тіла СсК

обчислюється за формулою:

V = ЦІ ахсіусіг . (3.29)

Обчислення маси матеріального тіла О а К

Якщо матеріальне тіло С має об'ємну густину ц = \х(х,у,г), то маса

тіла обчислюється за формулою:

т = ІЦц(х, у, г) ахсіусіг. (3.30)

Середня густина

|і

сер

тіла О є відношенням маси тіла до його об'є-

му, тобто:

Щ\і(х,у,г)сіхсіусІ2

V ІЦсіхсіусіг

де )і{х,у,г) - густина тіла О у кожній точці.

192

§3.

Застосування кратних інтегралів

Статичні моменти тіла

відносно координатних площин знахо-

дяться

за

формулами:

Д|д-цскаусії,

ДС^Н-йхаусіг , М

ху

^г^ахаусіг

осо

Координати центра ваги тіла

визначаються

за

формулами:

уг

ху

або

'»

Ус

=— [\\х\іскаусІ2 , у

= —

[[{у\ісіхауа'2

, г =—\\\2\іахауа2,

у т

де

т -

маса тіла

О.

При

р. =

маємо

=уІ}\

хахс1

Ус =~\\\уахауа2 , 2

-іД[г

ахауск,

о с

де

V -

об'єм тіла

С .

Моменти інерції тіла

відносно осей координат відповідно знахо-

дяться

за

формулами:

)И«М^, І

Д/^

+х

)\іахаусІ2,

= Д/О

+у

)[ісіхаусі2

II.

Контрольні питання

та

завдання

Як

обчислити площу замкненої обмеженої області?

Яку

фігуру можна назвати криволінійним циліндричним

тілом,

і як за

допомогою подвійного

або

потрійного інтеграла

обчислити його об'єм?

Як

обчислити площу поверхні,

яка

проектується

на

пло-

щину

хОу у

обмежену замкнену область?

Як

обчислити масу пластинки

тіла, якщо відома поверх-

нева

або

об'ємна густина

кожній точці?

Глава 3. Кратні інтеграли

193

///. Приклади розв'язання задач

Приклад 1. Обчислити площу фігури И, яка обмежена

параболою у = х

- 2х та прямою у = х.

• Побудуємо фігуру О за рівняннями її межі (рис.3.19).

у = х

Розв'язавши систему рівнянь у

, знайдемо, що х, = 0,

[у = х

= 3; _у, = 0, у

= 3 відповідно. Отже, лінії, що обмежують область, пе-

ретинаються в точках 0(0,0) та А/(3,3).

Область £) задається системою нерівностей:

£>:0<х<3,х-2х<у<х.

Тоді

8 = Цахау= |Л ^ау =](х-х

+2х)ах

••

О 0

2-2х 0

(г

— X

Приклад 2. Обчислити площу фігури, яка обмежена лем-

ніскатою Бернуллі з рівнянням: (х

+ у

)

= а

(х

- у

) .

• Оскільки лемніската Бернуллі (рис.3.20) симетрична відносно ко-

ординатних осей, то 5 = 45

у,

Рис.3.20

194

§3.

Застосування кратних інтегралів

Перейдемо до полярних координат х = рсозф, у = рзіпф, тоді рів-

няння лемніскати перетвориться на рівняння

(р

соз

ф + р

зіп

ф)

= я

(р

соз

ф-р

зіп

ф),

=а

(соз

ф-5Іп

ф), р

=а

со$2ф.

і л

Враховуючи, що р > 0, маємо р =

а-уісо&іт

, 0 < ф < — .

Тоді

8 = 48

=4^ахау =

х = рсозф, Д—>£),

у =

рзіпф,

Б : 0 <р <

ЙД/С032Ф,

сіх

ау = р ф

дер,

0 < ф <

4 а^/соз2(р 4

= 4||рфа'ф= 4|а"ф |рф=4|

її ооо

Г 2

0 0

о"ф

= 4—|соз2фй?ф = а

(зіп2ф)

2 0

Приклад 3. Знайти об'єм тіла О , обмеженого циліндра-

ми у =

л/х

_у

2л/х

та площинами х + г = 4 , г = 0.

• Задане тіло С обмежено зверху площиною х + г = 4, знизу пло-

щиною 2 = 0 і з боків прямими циліндрами у = 4х, у = 2*[х (рис.3.21а)).

Область інтегрування Б = х\^

х0у

С зображена на рис.3.21 б).

а) б)

Рис.3.21

Глава 3. Кратні інтеграли

195

Змінна х змінюється від 0 до 4, тобто 0 < х < 4; при будь-якому зна-

ченні з цього проміжку V* < у < 2л[х . Крім того, г = 4 - х.

Отже,

4 2-Гх 4 2л/7

V = \\{4-х) сіхсіу = \ііх

І(4-х)сіу

= \(4-х)у сіх =

о о £ о 4~

\ ( 1 З Л

|(4-Х)(2Л/7-Л/7)С&=

(4~х)4хах=

4х

-х

сіх •

.2 І 2 Р

4-х

З 5

64 64 _ 128

З 5 ~ 15

Приклад 4. Обчислити об'єм тіла, яке обмежене цилінд-

ром х

+ у

= Кх і сферою х

+ у

+ г

= К

(х > 0), за допо-

могою подвійного інтеграла.

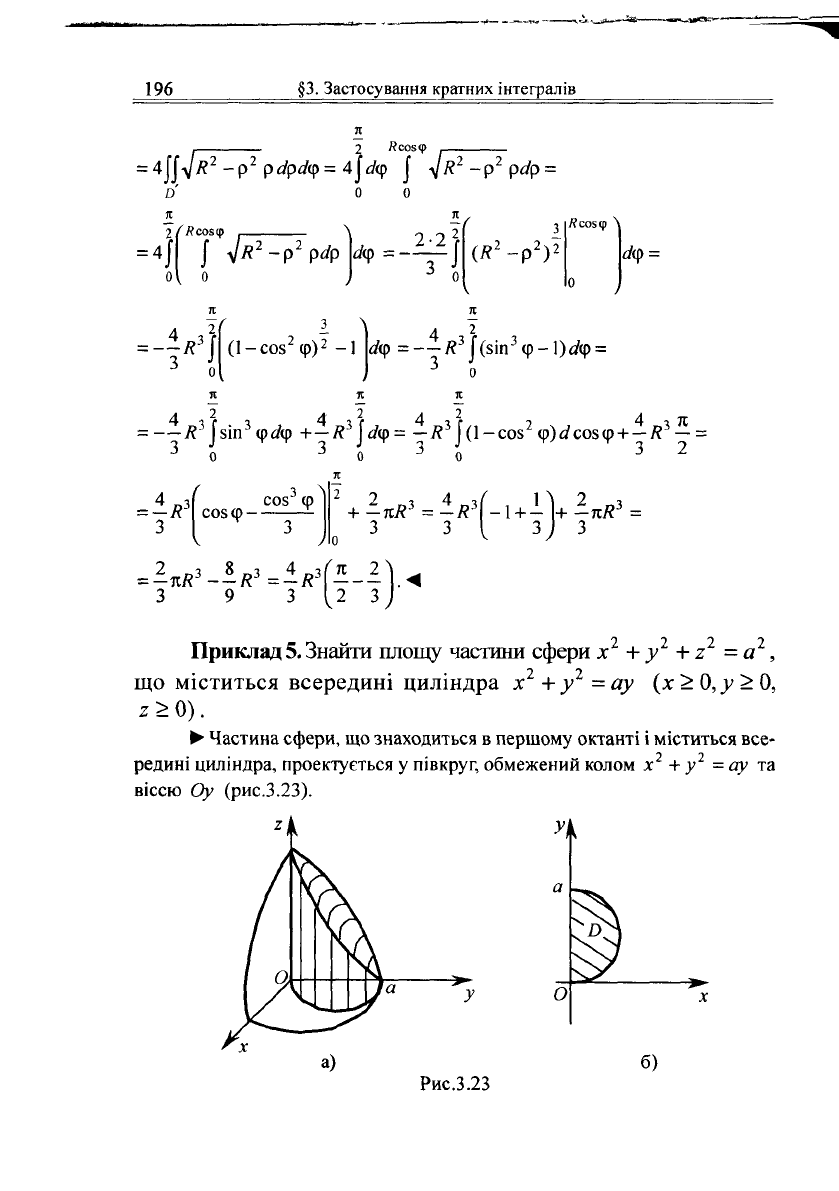
• Перша поверхня є циліндр із твірною, паралельною осі Ог, і на-

прямною:

( /0

х + У =

+ У =

, друга-сфера із центром у початку коорди-

нат і радіусом К . Від перетину двох поверхонь утворюється тіло, яке має дві

симетричні частини відносно площини хОу. Проекцію цього тіла на площину

хОу зображено на рис.3.22. Це є круг. На рисунку заштриховано область £> -

півкруга. Об'єм тіла обчислюється за формулою (3.24), де 2 = д/л

-х

-у

Враховано симетрію тіла і симетрію проекції цього тіла на площину хОу.

V =

лЦ^Я

-х

-у

сіхсіу =

Рис.3.22

д:

= рсо5ф, О-їО,

у = рзіпф, £> : 0 < р < /ссохф,

сіх сіу = р сір

сіц>,

0<ф<—.

196

§3.

Застосування кратних інтегралів

2 Лсо5ф

4[[д/#

-Р

рфЛр= 4|Лр І >/^

-Р

РФ =

2 / йсозф

/Л

-Р

РФ <*Р=™^}

(Л

-Р

)

ЙС05ф

*йр

(1-С05

ф)

- І аїр /?

|(зіп

ф-1)сЛр =

= --/?

|5ІП

фй?ф +

-Я

|й'ф

= -/г

|(1-С08

ф)й?С05ф + -Л

СОЗф-

з Л

СОЗ

З ЗІ 3 3

З 9 3 2 3

Приклад 5. Знайти площу частини сфери х

+ у

+ г

= а

що міститься всередині циліндра х

+у

=ау (х>0,у>0,

2>0).

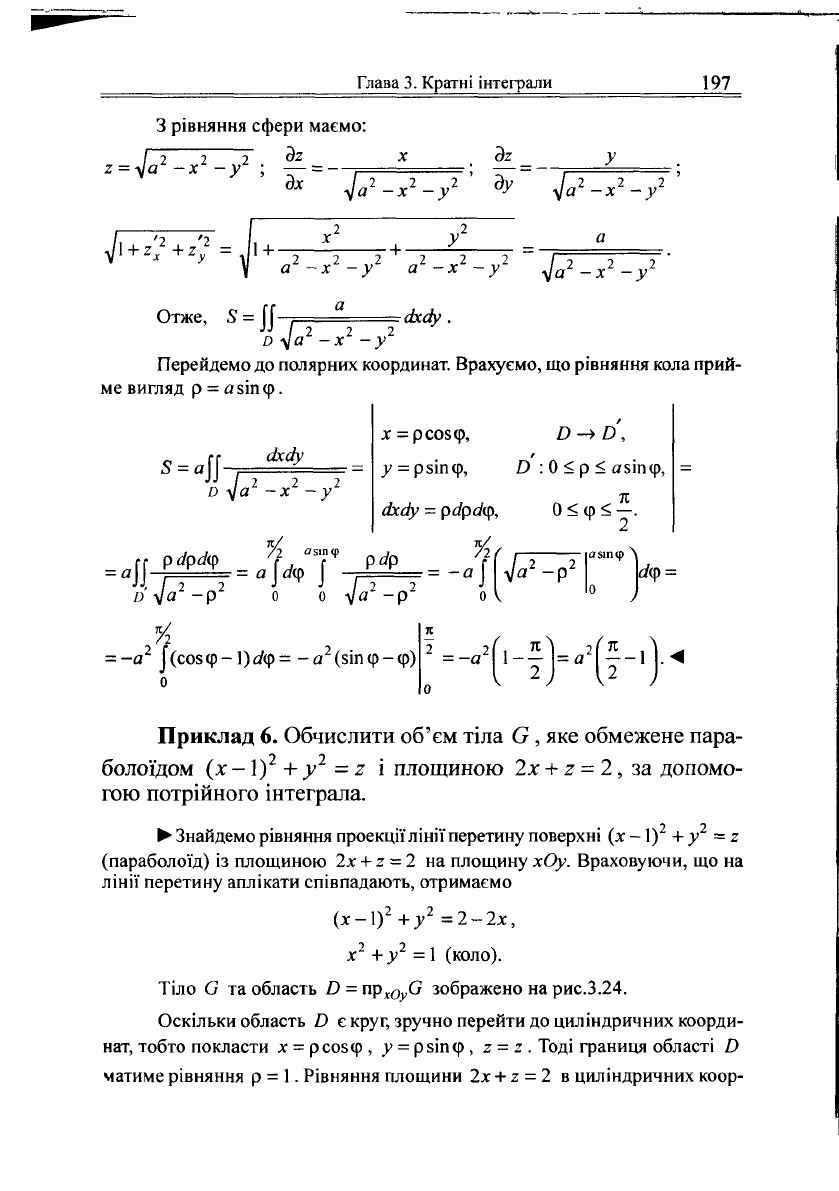
• Частина сфери, що знаходиться в першому октанті і міститься все-

редині циліндра, проектується у півкруг, обмежений колом х

+ у

= ау та

віссю Оу (рис.3.23).

б)

Рис.3.23

Глава 3. Кратні інтеграли

197

З рівняння сфери маємо:

Г1 т 7 дг

-X

-у

дх ^

г_

г ' ду

а -х -у а

-у

~У

Отже,

5 = ||

Перейдемо до полярних координат. Врахуємо, що рівняння кола прий-

ме вигляд р = азіпф.

5 = «||

йхау

-у

х= рсозф, £>-»£>,

у = рзіпф, £) : 0 < р < азіпф,

іхау = рфсЛр,

/2/

/ а$ши> \

ТС

0<ф<-.

гг

рф^ф ^. °7

Г п—

в\а -р о о V

~Р

в'

>/а

= -а

|(созф-1)й?ф = -а

(зіпф-ф)

а*Ф

=-а

(і-*

Приклад

6. Обчислити об'єм тіла О , яке обмежене пара-

болоїдом

(х-1) +у =г і площиною 2х

г = 2, за допомо-

гою

потрійного інтеграла.

•

Знайдемо рівняння проекції лінії перетину поверхні (х-1)

+ у

(параболоїд) із площиною 2х + г = 2 на площину хОу. Враховуючи, що на

лінії перетину аплікати співпадають, отримаємо

(х-1)

+у

=2-2х,

+у

(коло).

Тіло О та область О = пр

Юу

0 зображено на рис.3.24.

Оскільки область Б є круг, зручно перейти до циліндричних коорди-

нат, тобто покласти х = рсозф , у = рзіпф, г = г . Тоді границя області £)

матиме рівняння р = 1. Рівняння площини 2х + г = 2 в циліндричних коор-

198

§3.

Застосування кратних інтегралів

динатах є

т.

= 2(1 -рсозф), а рівняння параболоїда, яке запишемо так:

г-х

- 2х +1 + у

, матиме вигляд 2 = р

- 2р соз ф + 1, причому: 0<ф<2я,

0 < р < 1.

а)

б)

Рис.3.24

Змінна г змінюється від г=р -2рсозф+1 до і = 2(1 -рсозф).

Отже, р

-2созф+1 < г < 2(1

—

рсозф), бо область С7 обмежена знизу па-

раболоїдом, зверху - площиною. Об'єм тіла, обмеженого параболоїдом і

площиною, обчислюється так:

2к 1

2(1-рсозф)

V = Щсіхауаг = /Дрф сЦсЬ = | <Ар|рф ^сії =

о о

р -2рсо8ф+1

2л 1

0 0

2л 1

2(1-рС08ф)

2к 1

ф = | Лр|р(2-2рсозф-р

+2рсозф-1)ф:

-2рС05ф+1

|<*р|(р-р

)ф =

2л

0 0

Р Р

= 271

1-І

2 4

Приклад 7. Обчислити об'єм тіла С, яке обмежено по-

верхнею (х

+ у

)

=а

(х

+ у

)

за допомогою потрійно-

го інтеграла.

• Перейдемо до сферичних координат, поклавши х = гсозфзіпб,

у - /-зіпфзіпв, г = гсоз0. Тоді рівняння поверхні прийме вигляд:

= а

зіп

0 або г = язіп

0; отже 0 < г < азіп

0, 0 < 0< я. Об'єм тіла

обчислюється так:

Глава 3. Кратні інтеграли

199

2к К

0 51П 6

^ IX. IV, \А ані и

=2]І\скфа2

= 2Щг

$твсІгсІ(рсІв= |аїрІзіпОоВ \г

сіг =

:2гс[зіпЄ

2 з

= —па

2 з

—па

Я81П

о о

з"

я к к

соз0|*

-3]"соз

ва'созв + ЗІсоз

в «^созв-|соз

с/созв

-2-соз 0 +-соз

в,

Іо 5 іо

2па 6 2

64 з .

-2+2—+- =

5 7 105

Приклад 8. Обчислити масу та середню густину пластин-

ки О, яка обмежена лініями у = х

, у = \, якщо густина виз-

2 2

начається функцією \і(х, у) = х + у .

• Пластинка І) зображена на рис.3.25.

-4

у =

.у = *

-1

Рис.3.25

Обчислимо масу пластинки £):

/и =

||р(х,

у)ахау = ||(х

+ у

)ахау = ]ах](х

)ау-

і і

-і х

' 2 /

х у + —

і/

б >

ах = х

-х

н ах =

•І З З

/"З

х х

? \

1 Г

У~ 2Ї

105

Знайдемо ну пластинки £>, враховуючи симетрію пластинки

відносно осі і,. .

5 = ^

сіхау

= 2$$

сіх

сіу = 2$ сіх $ сіу = 2\{у\\ )сіх = 2|(1 -х

)сіх =

о о

= 2

(

)

ґ,

= 2

—

V /

Тепер обчислимо середню густину пластинки и.

сер

т 44-3 11 ^

*сєр

5 105-4 35

Приклад 9. Знайти статичні моменти М

та М

віднос-

но осей координат та центр ваги С(х

,у

) однорідної пластин-

ки О, обмеженої кривою у = зіп х, 0 < х <

тс

та віссю Ох (гус-

тина \і(х,у) = \).

• Пластинка О зображена на рис.3.26.

Рис.3.26

= Цу<&<іу = І

сіх

| у

сіу

= |

о о

1г

= —1(1 -соз2д:) сйг =

5Іп2х

( 2

5іп л:

"7*

= —|зіп

хсіх

••

11. ОЦІ .1 /І

= ^хсіхсіу

= |хЛ |ф

^хьтхсіх

-хсо$х

о о

к втх

+ |созд:а&ґ =

7І.

о о

||сіхсіу

- |йбс |ф = |зіпл:й&г = ~со5х|* = 2.

о оо

Отже,