Тевяшев А.Д., Литвин О.Г., Кривошеєва Г.М. та ін. Вища математика у прикладах та задачах. Ч 2

Подождите немного. Документ загружается.

Глава

Кратні інтеграли

161

Геометричний зміст подвійного інтеграла. Якщо /(х,у)>0

в об-

ласті

Б , то

подвійний інтеграл чисельно дорівнює об'єму

циліндрично-

го тіла,

яке

знаходиться

над

площиною

хОу,

нижня основа якого

область

£),

верхня

частина поверхні

г =

/(х,у),

що

проектується

в й , а

бічна

поверхня

циліндрична,

твірною, паралельною

осі Ог, і

напрямною

Ь -

межею області

(рис.3.1).

2=/(х,у)

то

Рис.3.1

Властивості подвійного інтеграла

1°.

\\с/(х,у)ахсіу=с\1/(х,у)ахау,

де С =

сопзІ.

2°.

Я (/і (х, У) +

(х, у))ах сіу

\\/

(х, у)

сіх сіу

\\ /

(х, у) сіх сіу.

І) й

3°.

Якщо функція

2 =

/(х,у)>0

області

й , то

Ц/(х,у)сіхсіу

>0.

4°.

Якщо

дві

функції

області

задовольняють нерівності

Дх,у)>8(х,у),

\\Кх,у)сЬссіу

\\§{х,у)сіхау.

5°.

Якщо область

складається

із

двох областей

£>, і

£>

як

не

ають спільних внутрішніх точок,

то

\\У(х,у)сіхсіу

\\у(х,у)сіхсіу+\\у(х,у)сіхсіу.

6° (Оцінка подвійного інтеграла). Якщо

г =

/(х,уО

неперервною

функцією

обмеженій замкненій області

О , яка

має

площу

5 , то

162

§1.

Подвійні інтеграли

т8йЦ/(х,у)ахау<М8,

де т і М -відповідно найменше і найбільше значення функції 2 = /(х,у)

в області Б.

7° (Теорема про середнє значення функції г = /(х,у)). Якщо функ-

ція 2 = /(х,у) неперервна в обмеженій замкненій області Б, яка має пло-

щу 5 , то в цій області існує хоча б одна точка Р(^,ц) така, що

Ц/(х,у)ахау

= /£,г])-8.

Обчислення подвійного інтеграла

Означення. Область Б називається правильною у напрямі осі Оу (осі

Ох),

якщо будь-яка пряма, яка проходить через внутрішню точку області Б,

паралельно осі Оу (осі Ох), перетинає межу області в двох точках М і N .

Якщо область Б (рис.3.2) правильна у напрямі осі Оу і проектується

на вісь Ох у відрізок [а,Ь], то її межа розбивається на дві лінії: АтВ, яка

задається рівнянням у =

(р

(х),

і АпВ, рівняння якої у = ф

(х) • Тоді об-

ласть Б задається системою нерівностей:

Б: а<х <Ь, <р

(х) < у < ф

(х)

у=<р

(х)

Ь х

Рис.3.2

При такому заданні області Б подвійний інтеграл по цій області Б

обчислюється за формулою:

(дг)

1\/(х,у)ахау

= \ах \/(х,у)сіу. (3.2)

О а <р,(д;)

Ь ф

(-0

Інтеграл ]ах ]/(х,у)сІу називається повторним або двократним.

а ф|(л)

Інтеграл

]/(х,у)ау

називається внутрішнім інтегралом. В ньому інтег-

Глава 3. Кратні інтеграли

163

рування ведеться по змінній у , а х вважається сталою величиною. Отже

І>

Ч>2(*)

\ах

1/(х,у)ау

ф,(дг)

І/(х, У) сіу

ФіОО

сіх.

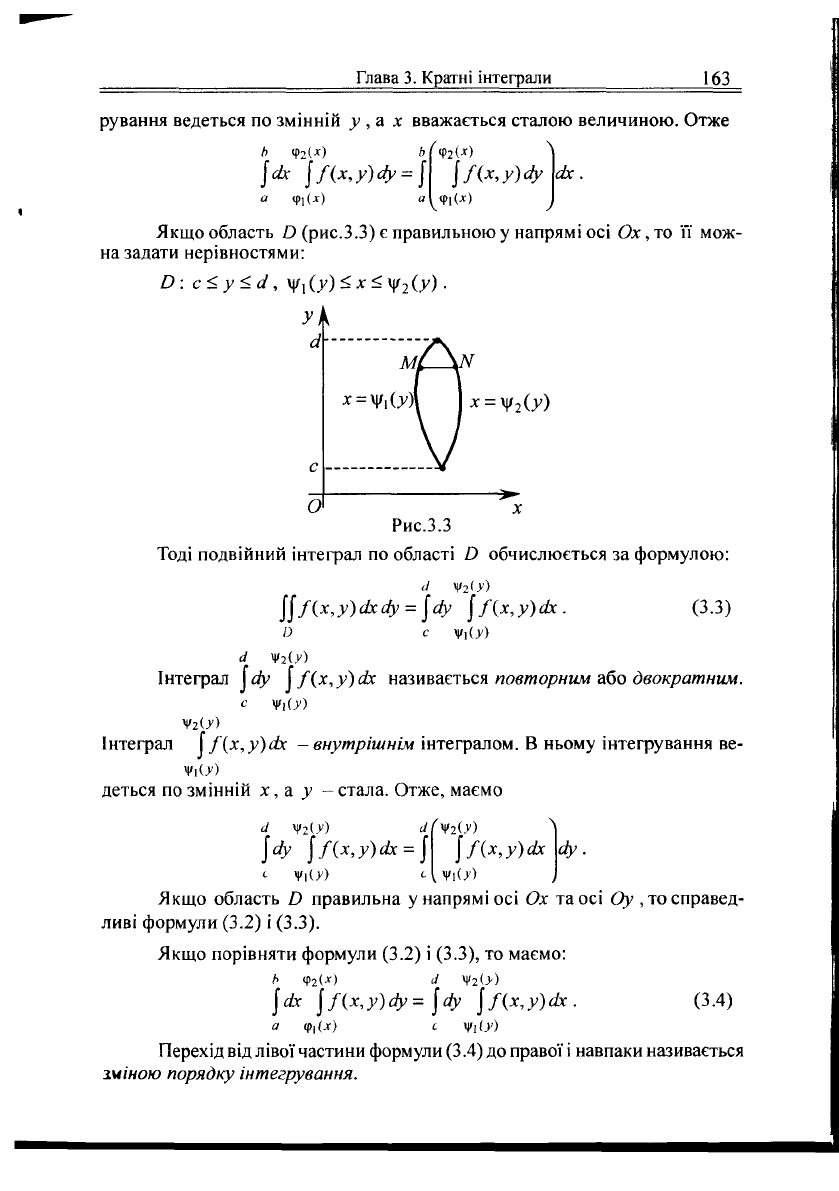
Якщо область О (рис.3.3) є правильною у напрямі осі Ох, то її мож-

на задати нерівностями:

Б: с<у<сі, у

(у)<х<у

(у).

сі

Рис.3.3

Тоді подвійний інтефал по області й обчислюється за формулою:

Ц/(х,у)сіхсіу =

Ісіу

\Ях,у)сіх.

(3.3)

О с Уі (у)

і Чг(У)

Інтеграл |ф ^/{х,у)сіх називається повторним або двократним.

с щ(у)

Інтеграл |/(х,у)ах - внутрішнім інтегралом. В ньому інтегрування ве-

Чі(У)

деться по змінній х, а у - стала. Отже, маємо

сі

4(уг(у)

\<Ь>

\/(х,у)сіх

= \

\/(х,у)сіх

сіу.

<• Чі(У)

<-\.Чі(У)

Якщо область О правильна у напрямі осі Ох та осі Оу , то справед-

ливі формули (3.2) і (3.3).

Якщо порівняти формули (3.2) і (3.3), то маємо:

Ь ф

(*) <1 ЧгІУ)

\сіх

\/(х,у)сіу=\сіу

\/(х,у)сіх.

(3.4)

а <р,(х) с VI (У)

Перехід від лівої частини формули (3.4) до правої і навпаки називається

зміною порядку інтегрування.

164

§1.

Подвійні інтеграли

(3.5)

Зауваження 1. Якщо область О не є правильною ні у напрямі осі Ох,

ні у напрямі осі Оу , то таку область необхідно розбити на частини, кожна з

яких є правильною областю у напрямі осі Ох чи осі Оу .

Зауваження 2. У кожному конкретному випадку, залежно від області

Б та підінтегральної функції Дх, у), треба обирати той порядок інтегру-

вання, який приводить до простіших обчислень.

Заміна змінних у подвійному інтегралі. Нехай задано дві прямо-

кутні декартові системи координат хОу та ИОУ , причому х і у пов'язані

зі змінними и і у формулами:

\х =

х(и,

у),

\у = у(и,у).

Формули (3.5) встановлюють взаємно однозначну відповідність між

точками М(х,у) області Б площини хОу і точками М'(и,у) деякої об-

ласті Б' площини иОу . Якщо визначник

дх дх

ди ЗУ

ду ду

ди ЗУ

то має місце формула (3.7)

—

загальна формула заміни змінних у подвійному

інтегралі:

ІІЯх,у)<Ьау

ЦЯх(и,у),у1и,у))\і\іЬіа\.

(3.7)

о о'

Функціональний визначник (3.6) називається визначником Якобі або

якобіаном.

1 =

*0.

(3.6)

Перехід до полярних координат. Прямокутні декартові координати

у і полярні координати р і ф зв'язані співвідношенями:

Якобіан / =

(0<р<+оо,

0<ф<2л).

СОЗф

-р51Пф

5ІПф

рС08ф

= рСОЗф,

У = р8ІПф,

дх

Зр

Зф

ду

Зр

Зф

Тоді

формула переходу до полярних координат

набуває вигляду

\\Кх,у)ахау = \\

Др

соз

ф,

зіп

ф) р

с/ф,

(3.8)

о /У

де область Б задана у декартовій системі координат хОу, а область £)' -

відповідна їй область у полярній системі координат.

Глава

Кратні інтеграли

165

Перехід

до

узагальнених полярних координат. Декартові

та

уза-

гальнені полярні координати зв'язані співвідношеннями:

х =арсозф

у=6р5Іпф, (0<р<

°о,

0<ф<2л,

а>0, Ь>0).

У даному випадку

| /1 = аЬр , а

формула переходу

до

узагальнених

полярних координат

має

вигляд:

Л/(х,у)ахау

Л/(арсо$у,

6рзіпф)а6рфй?ф,

(3.9)

де область

£)

задана

декартовій системі координат

хОу, а

область

й' -

відповідна

їй

область

узагальненій полярній системі координат.

//. Контрольні питання

та

завдання

Дайте означення подвійного інтеграла.

Наведіть приклади функції, для якої не існує подвійний

інтеграл.

Наведіть приклади області

В, для

якої

не

існує под-

війний інтеграл.

Яка область називається правильною

напрямі осі

Ох ;

у напрямі осі

Оу ?

Як

задати аналітично правильну область

напрямі

осі

Ох

; у

напрямі

осі Оу

Як

обчислювати подвійний інтеграл?

Які межі інтегрування для області

В,

яка

прямокутником?

8. Запишіть загальну формулу заміни змінних

подвійно-

му інтегралі.

9. Які межі інтегрування

повторному інтегралі, коли

В'

є коло

радіусом

і? і

центром

полюсі полярної системи?

10.

Які

координати називають узагальненими полярними

координатами? Чому дорівнює для таких координат якобіан?

166

§1.

Подвійні інтеграли

///.

Приклади розв'язання задач

Приклад 1. Обчислити подвійний інтеграл | [

т-сіхсіу,

де И - прямокутник (0 < х < 1, 0<у<1).

•

Область Б (рис.3.4) є правильною як у напрямі осі Оу , так і осі Ох.

У*

Рис.3.4

Тоді за формулою (3.2) маємо:

її -ахау=\ах\

т-ау=

\х

ах\

"і + у •Н і„2 •> ^

ау

]х

сіх (агс1

у||,) = ^-

о о

] +

о о

+ у

л _ 1 л _ л

~4~

3 1~ 12

Зауважимо, що у цьому прикладі внутрішній інтеграл має сталі межі

інтегрування і тому він дорівнює сталій величині. У даному випадку под-

війний інтеграл перетворився на добуток двох визначених інтегралів.-^

Приклад 2. Знайти межі інтегрування подвійного інтег-

рала || /(х,у)ахсіу, якщо область £> є трикутник, обмежений

лініями:у

= 0,

у-2-х,

х = 0 .

•

Область Б (рис.3.5) є правильною як у напрямі осі Оу , так і осі Ох.

Тоді за формулою (3.2) маємо:

7-х

11/(х,у)ахау = Іах \/(х,у)ау.

Глава 3. Кратні інтеграли

167

Рис.3.5 <

Приклад 3. Змінити порядок інтегрування у повторному

1 2-х

інтегралі | ах ^ /(х,у)сіу .

0 -Лс

• Область інтегрування £> (рис.3.6) обмежена лініями х = 0, х = 1,

у = >/х, у = 2 - х . З останніх двох рівнянь маємо: х- у

, х = 2- у .

1 2\у-2-

Рис.3.6

Пряма у = 1 розбиває область О на області £), і £>

Д:

0<у<1,

0<х<>>

, £>

: 1 < у < 2, 0<х<2-у.

Отже,

1 2-х 1 .у

2 2-у

| Дх,у-)^ = \ау\/{х,у)ах + \ау \ї(х,у)йх.<

0 ^ 0 0 10

2 д:

Приклад 4. Обчислити повторний інтеграл | ох| у сіу.

1 о

2 *

Г*

>• \ах^уау-\ \усіу ах= \

До ] і

і о

-х

сіх = \—сіх= —

2 6

168

§1 Подвійні інтеграли

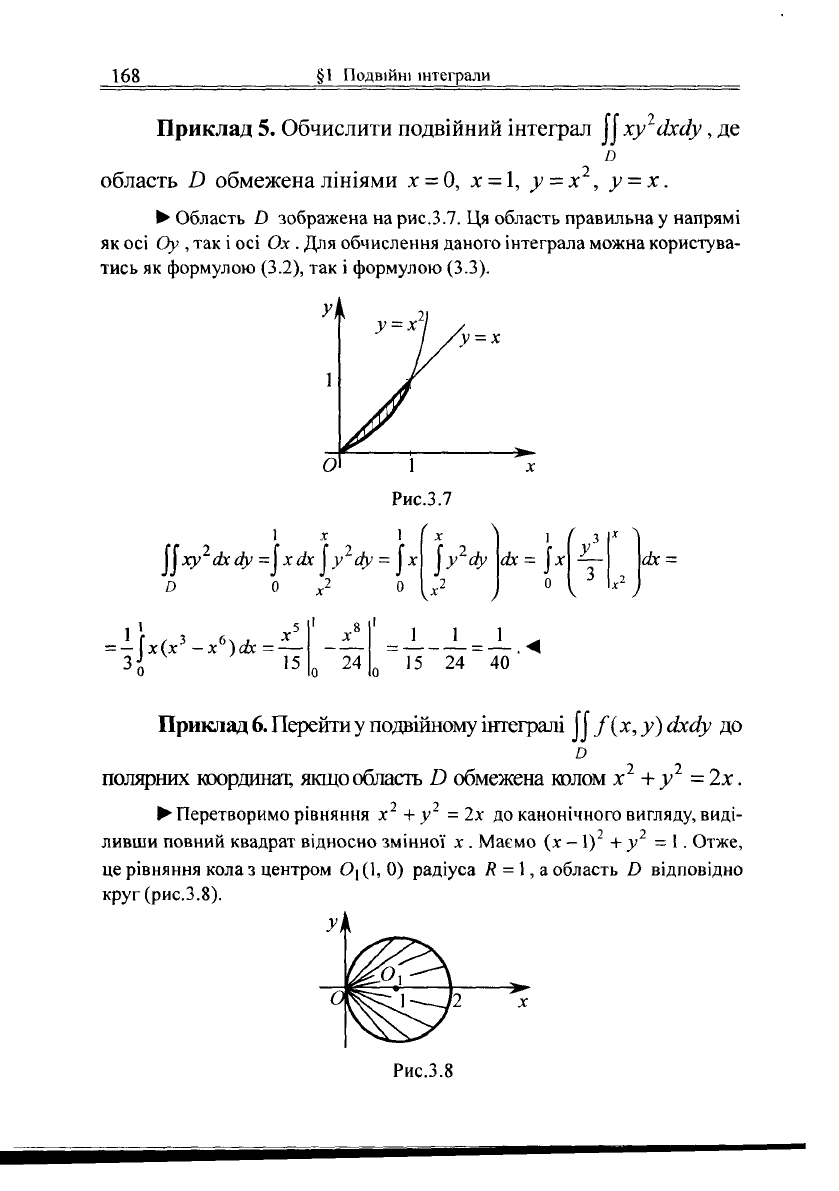
Приклад 5. Обчислити подвійний інтеграл ^ху

сіхсіу, де

область В обмежена лініями х = 0, х =

у -х , у = х.

• Область й зображена на рис.3.7. Ця область правильна у напрямі

як осі Оу , так і осі Ох . Для обчислення даного інтеграла можна користува-

тись як формулою (3.2), так і формулою (3.3).

Приклад

Перейти

податному інтегралі Д /(х, у) ахсіу до

полярних координат, якщо область £> обмежена колом х

+ у

=2х.

• Перетворимо рівняння х

+ у

=2х до канонічного вигляду, виді-

ливши повний квадрат відносно змінної х. Маємо (х -1)

+ у

= 1. Отже,

це рівняння кола з центром 0\

(1,

0) радіуса Я = 1, а область /> відповідно

круг (рис.3.8).

Рис.3.8

Глава 3 Кратні інтеграли

169

Перейдемо до полярних координат х = р созф, у = р зіп ф, тоді рівнян-

ня кола набуває вигляду р = 2созф, причому змінна ф задовольняє умові:

71 71

-— < ф < —, бо р > 0, а 0 < р < 2созф.

Тоді за формулою (3.8) маємо

Ц/(х,у)ахау

х = рсозф, £)—>£>',

_у = рзіпф, £>': 0 < р < 2созф,

сіхсіу = р фа?ф,

71 ТІ

-— < ф < —.

2 2

2 2совф

= Лдрсозф,рзіпф)рфс/ф = |

</ф

|/(рС03ф,р5ІПф)рфбЛр. Ч

О' _л 0

х у

сіхсіу, де область £) є

круг радіуса Л з центром у початку координат: х

+ у

<К

• Зробимо заміну змінних: х =

рсозф,

і>

рзіпф,

тоді рівняння

+ у

= К

перетвориться на р = К (0 < ф < 2к). Тоді за формулою (3.8)

маємо:

2 2

-де -у

2 л Я

х = рсозф, Б -> О',

у^рзіпф,

й':0<р<К,

сіхау = р фс/ф, 0 < ф < 2тг.

Це

рфіф =

2кґК

2п

( ]

|с/ф|е

_р

рф = |

_[е~

рф «Лр = |

|е^

^(-р

)

о о

2ті/

0 \ 0

сЛр =

1-е"

Приклад 8. Обчислити подвійний інтеграл

їИ

2 2

ДГ V

де область £) обмежена еліпсом

-^г-

—г-

= 1

170

Подвійні інтеграли

• Перейдемо до узагальнених полярних координат, поклавши:

х = ар соз ф, у = Ьрзіпф. Тоді рівняння еліпса у цих координатах:

С05

ф І

ЗІП

-—-+

-—- =

=> р =1 =» 0 = 1.

Отже, 0 < р < 1. Кут. ф змінюється від 0 до 2%. Тоді

х = арсозф, £> -> І)',

у = фзіпф, О':0<р<1,

адсау = аЬр фаїр, 0 < ф < 2к.

. 2я 1 .

Дд/1-р

я*р ф<Ар = ай| а"ф|у1-р

РФ =

= аЬ-2к

1 2(1 -р

/2 >

о о

= —паЬ. <

IV. Задачі для практичних занять

задачах 3.1-3.9 обчислити повторні (двократні) інтеграли.

3.1.

1 2

]сіх]хусіу.

1 1

3.3.

[сіх\ -сіу.

1 і

3.5.

\ах\е

х+у

сіу.

2 1п>>

3.7.

сіу

\е

сіх.

і о

і і

3.9.

сіх

о(

х +

У +

-сіу.

2Ь а

3.2.

]сіх](а- у)х

сіу.

0 о

2 £

3.4.

|ф |р$іпф

<Лр.

1 о

а -їх

3.6.

Іф

4 2х

3.8.

\сіх сіу.

2 х